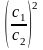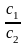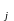Как найти диаметр параболы

Макеты страниц

643 Составить уравнение диаметра
эллипса , проходящего через
середину его хорды, отсекаемой на прямой . 644 Составить
уравнение хорды эллипса , проходящей
через точку А(1; -2) и делящейся ею пополам. 645 Составить
уравнения двух взаимно сопряженных диаметров
эллипса , из которых один образует
с осью Ох угол 45⁰. 646 Составить
уравнения двух взаимно двух взаимно сопряженных
диаметров эллипса , из которых один
параллелен прямой . 647 Составить
уравнения двух взаимно сопряженных диаметров
эллипса , из которых один
перпендикулярен к прямой . 648 На чертеже
изображен эллипс. Пользуясь циркулем и линейкой,
построить его центр. 649 Доказать, что оси
эллипса являются единственной парой его главных
диаметров. 650 Пользуясь
свойствами сопряженных диаметров, доказать, что
каждый диаметр окружности является главным.
651 а). В эллипс вписан
равнобедренный треугольник так, что его вершина
совпадает с одной из вершин эллипса. Доказать,
что основание этого треугольника параллельно
одной из осей эллипса; б). Доказать, что стороны
прямоугольника вписанного в эллипс,параллельны
осям этого эллипса; в). На чертеже изображен
эллипс. Пользуясь циркулем и линейкой, построить
его главные диаметры.
652 Доказать, что хорды
эллипса, соединяющие его произвольную
произвольную точку с концами любого диаметра
этого эллипса, праллельны паре его сопряженных
диаметров.
653 а). Доказать, что
сумма квадратов двух сопряженных полудиаметров
эллипса есть величина постоянная (равная сумме
квадратов его полуосей), б). Доказать, что площадь
параллелограмма, построенного на двух
сопряженных полудиаметрах эллипса, есть
величина постоянная (равная площади
прямоугольника, построенного на его полуосях).
654 Составить
уравнение диаметра гиперболы , походящего
через середину ее хорды, отсекаемой на прямой .
655 Дана гипербола . Составить уравнение ее хорды,
которая проходит через точку А(3; -1) и делится
точкой А пополам.
656 Составить
уравнениядвух сопряженных диаметров гиперболы , из которых один проходит через точку
А(8; 1).
657 Составить
уравнения сопряженных диаметров гиперболы , угол между которыми равен 45⁰.
658 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее центр.
659 Доказать, что оси
гиперболы являются единственной парой ее
главных диаметров.
660 На чертеже
изображена гипербола. Пользуясь циркулем и
линейкой, построить ее главные диаметры.
661 Составить
уравнение диаметра параболы , проходящего
через середину ее хорды, отсекаемой на прямой .
662 Дана парабола . Составить уравнение ее хорды,
которая проходит через точку А(2; 5) и делится
точкой А пополам.
663 Доказать, что ось
параболы является единственной ее главным
диаметром.
664 На чертеже
изображена парабола. Пользуясь циркулем и
линейкой, построить ее главный диаметр.

Уравнение диаметра проходящего через точку

Глава 22. Диаметры линий второго порядка

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением

(1)

то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Если гипербола задана уравнением

, (2)

то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

,

то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением

.

Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k ’ – угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то

(3)

Если k и k ’ – угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то

(4).

Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

Уравнение кривой второго порядка

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Диаметры кривой. Главные оси. Асимптоты. Уравнение кривой, отнесенной к сопряженным направлениям; уравнение кривой, отнесенной к асимптотам.

Если в кривой второго порядка провести все хорды одного и того же направления, то геометрическое место середин этих хорд представит некоторую прямую, которую называют диаметром, сопряженным данным хордам. Уравнение диаметра:

где есть угловой коэффициент сопряженных хорд. Меняя , т.е. меняя направление хорд, получим бесчисленное множество диаметров; все они проходят через центр кривой. У параболы все диаметры параллельны между собой.

Направление хорд и направление сопряженного им диаметра называются сопряженными направлениями относительно данной кривой. Зависимость между двумя сопряженными направлениями следующая:

Сопряженными диаметрами называются такие два диаметра, из которых каждый делит пополам хорды, параллельные другому. У параболы сопряженных диаметров нет, так как все диаметры имеют одно и тоже направление.

Главными осями кривой называются диаметры, перпендикулярные к сопряженным хордам; их направления называются главными направлениями.

В случае прямоугольной системы координат главные направления определяются из уравнения:

где – угол между одним из главных направлений и направлением оси .

В случае косоугольной системы координат имеем:

Всякая кривая второго порядка имеет два главных направления, за исключением окружности, для которой главные направления неопределенные.

Угловой коэффициент определяется для всех диаметров параболы по формуле:

если для старших коэффициентов параболы введены обозначения:

Главная ось параболы как один из ее диаметров имеет это же направление и в случае прямоугольных координат она изображается уравнением

Второе главное направление параболы перпендикулярно к ее диаметрам, но второй главной оси у параболы нет. Если отнести кривую у двум сопряженным направлениям, т.е. выбрать за оси координат прямые, имеющие сопряженные направления относительно этой кривой, то в уравнение кривой не войдет член с произведением координат (). У параболы кроме того, исчезнет ещё один из старших членов ().

Если центральную кривую отнести к двум сопряженным диаметрам (или к главным осям), то уравнение ее примет вид:

Простейшее уравнение параболы мы получим, поместив начало координат в вершину, т.е. в точку пересечения параболы с главной осью (), выбрав главную ось за ось абсцисс (, и ) и касательную в вершине (она перпендикулярна к оси) за ось ординат:

При таком же выборе осей координат центральная кривая изобразится уравнением

Асимптоты кривой можно рассматривать как те ее диаметры, которые сами себе сопряжены. Угловые коэффициенты асимптот определяются из уравнения

Асимптоты могут быть только у центральных кривых: гипербола имеет две действительные асимптоты, эллипс – две мнимые; в случае пересекающихся прямых асимптоты совпадают с этими прямыми.

Если принять асимптоты гиперболы за оси координат, то уравнение этой гиперболы примет вид:

587. Найти два сопряженных диаметра кривой , из которых один проходит через начало координат.

Решение . Данная кривая центральная, потому что . Уравнение всякого ее диаметра будет где – угловой коэффициент сопряженного диаметра. Так как искомый диаметр проходит через начало координат, то свободный член его уравнения должен равняться нулю, т.е. откуда . Вставив это значение параметра в общее уравнение диаметра и преобразовав его, получим: . Это уравнение одного из искомых диаметров; его угловой коэффициент ; следовательно, уравнение сопряженного диаметра будет:

588. Через точку (1;-2) проведен диаметр кривой . Найти уравнение этого диаметра и диаметра ему сопряженного.

589. Дана кривая . Найти ее диаметр, параллельный оси абсцисс, и диаметр, ему сопряженный.

590. Найти два сопряженных диаметра кривой , из которых один параллелен оси ординат.

591. Дана кривая и один из ее диаметров . Найти диаметр, ему сопряженный.

592. Составить уравнение диаметра кривой , параллельного прямой .

593. Определить диаметр кривой , образующий угол в с осью абсцисс. Угол .

594. Дана кривая: . Найти геометрическое место середин ее хорд: 1) параллельных оси ; 2) параллельных оси ; 3) параллельных прямой .

595. Найти диаметр кривой , проходжящей через середину хорды, отсекаемой этой кривой на прямой .

596. Найти середину хорды, отсекаемой кривой на прямой .

597. Найти такие сопряженные диаметры кривой , которые образуют между собой угол в . Угол .

598. Найти зависимость между угловыми коэффициентами прямых, имеющих сопряженные направления относительно:

1) эллипса ; 2) гиперболы .

599. Через точку (1;-3) провести хорду эллипса , сопряженную диаметру .

600. Найти направления и длину двух сопряженных диаметров эллипса , из которых один проходит через точку (2;3).

601. Найти угол между двумя сопряженными диаметрами эллипса , из которых один образует угол в с большой осью.

602. Определить длину тех сопряженных диаметров эллипса , которые образуют между собой угол .

Указание . В этой задаче удобно воспользоваться теоремами Аполлония: и , где и – полуоси эллипса; и – сопряженные полудиаметры его; – угол между этими сопряженными диаметрами.

603. Даны размеры двух сопряженных диаметров эллипса и и угол между ними . Вычислить длину его осей.

604. Определить угол между двумя сопряженными диаметрами гиперболы , зная, что действительный из этих диаметров втрое больше действительной оси.

605. Найти уравнения двух сопряженных диаметров гиперболы , угол между которыми равняется .

606. Дана парабола: . Написать уравнение диаметра этой параболы:

1) проходящего через начало координат;

2) сопряженного хордам, параллельным оси ;

3) сопряженного хордам, параллельным оси ;

4) образующего угол с сопряженными хордами;

5) перпендикулярного к сопряженным хордам.

Во всех случаях угол

607. Найти диаметр параболы , сопряженный тем хордам, которые наклонены под углом в к оси параболы.

608. Написать уравнение диаметра параболы , сопряженного с прямой .

609. Найти главные оси кривых:

Во всех случаях угол

610. Каковы будут главные оси распавшейся центральной кривой?

611. Найти ось параболы .

Решение . Все диаметры данной параболы имеют угловой коэффициент . Ось параболы есть диаметр, сопряженный перпендикулярным хордам, т.е. хордам с угловым коэффициентом (система координат предполагается прямоугольной). Уравнение всякого диаметра этой параболы будет при мы получим уравнение оси: .

612. Найти ось симметрии и вершину каждой из следующих парабол:

Во всех случаях угол

Указание . Вершина параболы находится как точка пересечение параболы с ее осью.

613. Найти общий диаметр двух кривых:

614. Составить уравнение кривой второго порядка, проходящей через начало координат, если известны две пары сопряженных ее диаметров:

Решение . Угловые коэффициенты сопряженных диаметров удовлетворяют уравнению: . Угловые коэффициенты данных диаметров: и , , ; вставляя эти значения в указанное уравнение, получим:

Координаты центра искомой кривой мы можем определить, решая совместно уравнения двух диаметров: , . Эти координаты должны удовлетворять уравнениям: и которые данном случае перепишутся так: и ; вставим вместо : и вычисленные их значения и тогда получим: и . Кроме того, кривая проходит через начало координат; значит, , и уравнение кривой будет:

615. Две пары прямых:

служат сопряженными диаметрами кривой второго порядка. Составить уравнение этой кривой, зная, что она проходит через точку (1;1).

616. Выяснить особенности в выборе осей координат, если кривые даны следующими уравнениями:

617. Относительно некоторой прямоугольной системы координат кривая дана уравнением: . Преобразовать это уравнение, приняв за оси координат главные оси кривой.

618. Отнести к главным осям кривые, данные относительно прямоугольной системы координат уравнениями:

619. Уравнение кривой, отнесенной к двум сопряженным диаметрам, составляющим угол , имеет вид: . Найти уравнение той же кривой относительно ее главных осей.

620. Отнести к главным осям кривые:

621. Выяснить особенности в выборе осей координат, если параболы даны следующими уравнениями:

622. привести к простейшему виду уравнение параболы ; .

623. Привести к простейшему виду уравнения следующих парабол:

624. Отнести к вершине следующие центральные кривые:

Во всех случаях .

625. Найти асимптоты следующих гипербол:

626. Доказать, что все кривые, уравнения которых отличаются друг от друга только свободными членами, имеют общие асимптоты. Найти, например, асимптоты кривых при различных значениях параметра λ.

627. Доказать, что если две кривые имеют общие асимптоты, то все члены их уравнений, кроме свободных членов, имеют пропорциональные коэффициенты.

628. Составить общее уравнение для всех кривых. Имеющих прямые и своими асимптотами.

629. кривая второго порядка проходит через точку (1;-1) и имеет своими асимптотами две прямые: и . Составить уравнение этой кривой.

630. Составить уравнение кривой, касающейся прямой и имеющей прямые и своими асимптотами.

630*. Какому условию удовлетворяют коэффициенты общего уравнения гиперболы, если гипербола равносторонняя?

631. Какой вид имеет уравнение гиперболы, если одна из осей координат или обе оси параллельны асимптотам?

632. Составить уравнение гиперболы, проходящей через точки (2;1), (-1;-2) и (), при условии, что одна из ее асимптот совпадает с осью абсцисс.

633. Уравнение гиперболы, отнесенной к главным осям, имеет вид: . Преобразовать это уравнение, приняв асимптоты гиперболы за новые оси координат.

634. Отнести гиперболу к ее асимптотам.

635. Как преобразуется уравнение гиперболы , если за оси координат принять ее асимптоты? Угол .

636. Сколько членов второй степени и какие именно могут войти в уравнение: 1) эллипса4 2) гиперболы; 3) параболы?

Преобразование уравнения кривой второго порядка с помощью инвариантов.

Если одна и та же кривая второго порядка, отнесенная к двум различным произвольно выбранным системам координат с координатными углами и , изображается уравнениями:

то имеют место следующие равенства:

т.е. существуют выражения, составленные из коэффициентов уравнения кривой и соответствующего координатного угла, которые не меняют своей величины ни при каком преобразовании декартовых координат. Такие выражения называются инвариантами кривой второго порядка. Мы можем пользоваться тремя вышеприведенными инвариантами:

для упрощения уравнений кривой второго порядка, если только уравнение кривой после преобразования содержит не более трех коэффициентов.

637. Пользуясь инвариантами, отнести к главным осям кривую , зная что .

Решение . Искомое уравнение имеет следующий вид:

Для прямоугольных систем координат инварианты упрощаются, так как и , и мы будем иметь: ; . Найдем числовое значение этих инвариантов, исходя из данного уравнения:

Составим теперь выражения этих же инвариантов через коэффициенты преобразованного уравнения: . Так как инварианты не меняют своей величины при преобразовании координат, то мы можем приравнять между собой найденные для них выражения, содержащие коэффициенты первоначального и преобразованного уравнения;. Из этой системы уравнений мы определяем неизвестные коэффициенты преобразованного уравнения: ;, и искомое уравнение будет . Таким образом, пользуясь инвариантами, можно привести уравнение кривой к простейшему виду, не отыскивая ее центра, осей и не составляя формул преобразования координат.

638. Пользуясь инвариантами, привести к простейшему виду уравнения следующих кривых:

при условии, что все они отнесены к прямоугольной системе координат.

639. Пользуясь инвариантами, упростить уравнения следующих кривых:

Во всех случаях .

640. Упростить уравнения следующих кривых:

640*. Отнести к главным осям кривую , если известно, что .

641. Отнести гиперболу к ее асимптотам, пользуясь инвариантами. Угол .

Решение . Уравнение кривой, отнесенной к асимптотам, имеет вид:

Нам надо найти два неизвестных коэффициента , и новый координатный угол , т.е. угол между асимптотами. Найдем числовую величину инвариантов, пользуясь данным уравнением, при , : . Выражения этих инвариантов в новых коэффициентах будут:

Для определения трех величин , и имеем три уравнения:

Решив их, получим: , ; и ; искомое уравнение будет: . Выбираем направление осей так, чтобы гипербола была расположена в нормальном угле и вертикальном к нему угле; тогда после упрощений получим: .

642. Отнести к асимптотам гиперболы, данные относительно прямоугольной системы координат уравнениями:

643. Относительно некоторой прямоугольной системы координат кривая изображается уравнением . Составить уравнение этой же кривой относительно ее вершины.

Указание . Отнести кривую к вершине – значит принять одну из осей кривой за ось абсцисс, перенести начало координат в вершину и принять касательную в вершине за ось ординат.

[spoiler title=”источники:”]

http://infourok.ru/uravnenie-krivoy-vtorogo-poryadka-2812642.html

[/spoiler]

В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, которые ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением.

x²/a² + y²/b² = 1 (1)

то его диаметр, сопряженный хордам с угловым коэффициентом k, определяется уравнением

y = – b²/a²k x.

Ести гипербола задана уравнением

x²/a² – y²/b² = 1 (2)

то ее диаметр, сопряженный хордам с угловым коэффициентом k, определяется уравнением

y = b²/a²k x.

Все диаметры параболы параллельны ее оси. Если парабола задана уравнением

у² = 2рх,

то ее диаметр, сопряженный хордам с угловым коэффициентом k, опредепяется уравнением

y = p/k.

Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.

Если k и k’ – угловые коэффициенты двух взаимно сопряженных диаметров гиперболы (2), то

kk’ = -b²/a² (3)

Если k и k’ – угловые коэффициенты двух взаимно сопряженных диаметров гиперболы (2), то

kk’ = b²/a² (4)

Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.

Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.

643. Составить уравнение диаметра эллипса x²/25 + y²/16 = 1 , проходящего через середину его хорды, от-секаемой на прямой 2х – у – 3 = 0.

644. Составить уравнение хорды эллипса x²/16 + y²/9 = 1, проходящей через точку A (1; -2) и делящейся ею пополам.

645. Составить уравнения двух взаимно сопряженных диаметров эллипса x² + 4y² = 1, из которых один образует с осью Ох угол в 45°.

646. Составить уравнения двух взаимно сопряженных диаметров эллипса 4х ² + 9y² = 1, из которых один параллелен прямой х + 2у – 5 = 0.

647. Составить уравнения двух взаимно сопряженных диаметров эллипса х² + 3y² = 1, из которых один перпендикулярен к прямой Зх + 2у – 7 = 0.

648. На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его центр.

649. Доказать, что оси эллипса являются единст-венной парой его главных диаметров.

650. Пользуясь свойствами сопряженных диаметров, доказать, что каждый диаметр окружности является главным.

651. а) В эллипс вписан равнобедренный треугольник так, что его вершина совпадает с одной из вершин эллипса. Доказать, что основание этого треугольника параллельно одной из осей эллипса.

б) Доказать, что стороны прямоугольника, вписанного в эллипс, параллельны осям этого эллипса.

в) На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его главные диаметры

652. Доказать, что хорды эллипса, соединяющие его произвольную точку с концами любого диаметра этого эллипса, параллельны паре его сопряженных диаметров.

653. а) Доказать, что сумма квадратов двух сопря-женных полудиаметров эллипса есть величина постоянная (равная сумме квадратов его полуосей). б) Доказать, что площадь параллелограмма, построенного на двух сопряженных полудиаметрах эллипса, есть величина постоянная (равная площади прямоугольника, построенного на его полуосях).

654. Составить уравнение диаметра гиперболы x²/5 – y²/4 = 1, проходящего через середину ее хорды, отсекаемой на прямой 2х – y + 3 = 0.

655. Дана гипербола x²/3 – y²/7 = 1. Составить уравнение, ее хорды, которая проходит через точку A (3; – 1) и делится точкой А пополам.

656. Составить уравнения двух сопряженных диаметров гиперболы х² – 4у² = 4, из которых один проходит через точку А (8; 1).

657. Составить уравнения сопряженных диаметров гиперболы x²/4 – y²/6 = 1, угол между которыми равен 45°.

658. На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить ее центр.

659. Доказать, что оси гиперболы являются един-ственной парой ее главных диаметров.

660. На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить ее главные диаметры.

661. Составить уравнение диаметра параболы у² = 12х, проходящего через середину ее хорды, отсекаемой на прямой Зх + у – 5 = 0.

662. Дана парабола у² = 20х. Составить уравнение ее хорды, которая проходит через точку А (2;5) и делится точкой А пополам.

663. Доказать, что ось параболы является единст-венным ее главным диаметром.

664. На чертеже изображена парабола. Пользуясь циркулем и линейкой, построить ее главный диаметр.

1. Линии эллиптического, гиперболического и параболического типов. Центры линий второго порядка.

Пусть
на плоскости A²(i)
выбран
некоторый репер и задано уравнение
линии второго порядка а₁₁x
+2
а₁₂x₁x₂
+ а₂₂x
+2
а₁х₁
+2а₂х₂
+
а
=
0. (1)

Векторы,
имеющие относительно линии (1)
асимптотические направ­ления,
определяются равенством а₁₁c
+2
а₁₂c₁c₂
+ а₂₂c
=
0. (2)

Пусть
вектор с
имеет
асимптотическое направление относительно
линии (1). Так как любой вектор

с,
где
а — произвольное, отличное от нуля
комплексное число, имеет то же направление,
то направление вполне определяется
заданием отношения с₁
:
с₂
координат
вектора с, если с₂
≠
0.
Мы будем употреблять запись с₁
:
с₂
и
в том случае, когда с₂
=
0, а именно: символ 1:0 задает направление
базисного вектора е
.

Пусть
а₁₁
≠ 0.
У вектора, имеющего асимптотическое
направле­ние, с₂
≠ 0,
так как в противном случае из равенства
(2) следует а₁₁c

=
0, а а₁₁
≠
0
и c₁
≠
0.
Запишем теперь равенство (2) в виде
а₁₁
+2
а₁₂
+
=0.

Решая
это квадратное уравнение относительно
c
/с₂,
получаем
=

Возможны
следующие случаи:

1)

–

<
0,
поэтому не существует действительных
асимптотических направлений относительно
линии (1), иначе, существует два мнимых
асимптотических направления;

1. –
   

   
   >
   0, следовательно, существует два
   действитель­ных асимптотических
   направления;

2. –
   

   
   =
   0, поэтому существует одно действительное
   асимптотическое направление.

Если

= 0, а₂₂
≠
0,
то, меняя ролями c

и
с₂,
приходим к тем же случаям.

Наконец,
пусть

= 0 и а₂₂
= 0. Тогда а₁₂
≠
0, и
уравнение (2) принимает вид а₁₂
c

с₂
= 0. В этом случае существует два
асимпто­тических направления,
определяемых векторами с(1, 0) и с'(0, 1).

Определение
5.1. Линия
второго порядка на плоскости A²
(i)
называется линией эллиптического,
гиперболического или пара­болического
типа в соответствии с тем, к какому из
трех указанных выше случаев она относится.

При
аффинных преобразованиях плоскости
А²(1)
линия
второго порядка не может изменить свой
тип, так как при этом действитель­ные
асимптотические направления переходят
в действительные.

1. Диаметральные плоскости. Диаметры линий второго порядка.

Пусть
в пространстве Aⁿ(i)
выбран
некоторый репер и задана квадрика

+2
=0
(1) Пусть,
далее, x
=b

+ c
t,
i=1,
2,
…, п,

(2) есть уравнения прямой, направляющий
вектор которой с(
c
,
c₂,
… , c
)

(3) имеет неасимптотическое относительно
квадрики (1) направление. Прямая (2)
пересекает квадрику (1)
в двух точках: М′
(x′
,
x′₂,…,x′
)
и
М″(
x″
,
x″₂,…,x″
),
быть
может, совпадающих.

Определение
7.1. Отрезок
М’М”, определяемый двумя точ­ками,
принадлежащими квадрике (1), называется
хордой этой квадрики.

Если
в качестве начальной точки В(b₁
,b₂,
…, b_n)
прямой
(2) взять середину хорды М’М”,
то
должно выполняться равенство (6) из §6:

+
=
0. (4)

(Если
М’
= М”,
то положим В
=
М’
= М″.)

Рассмотрим
теперь все прямые с заданным направляющим
вектором (3). Середины хорд, отсекаемых
на этих прямых квадри­кой (1), образуют
множество точек, определяемое уравнением



+
=
0, (5)

которое
получается из равенства (2)
заменой обозначений b

на
х
.
Уравнение (5) —линейное. В самом деле,
если в этом уравнении все коэффициенты
при х_j
—
нули, т. е.

=
0, j
= 1, 2, … , n,
то, умножая каждое из этих равенств
на соответствующее с, и сум­мируя по
j,
получаем

=
0,

т.
е., вопреки предположению, вектор (3)
имеет асимптотическое направление.
Таким образом, верна

Теорема
7.1. Множество
середин хорд, отсекаемых квадрикой (1)
на всех параллельных прямых с направляющим
вектором (3), имеющим неасимптотическое
направление, является гиперплос­костью
с уравнением (5).

Определение
7.2. Гиперплоскость
(5) называется диамет­ральной
гиперплоскостью квадрики (1), сопряженной
с направле­нием вектора (3).

Очевидно,
что диаметральная плоскость —
аффинное понятие.

Диаметры
линий второго порядка

Рассмотрим
плоскость A²(i).
Выберем
некоторый репер и зададим линию
второго порядка с уравнением а₁₁x
+2
а₁₂x₁x₂
+ а₂₂x
+2
а₁х₁
+2а₂х₂
+
а
=
0.
(1)

В
этом случае диаметральная гиперплоскость
является прямой и на­зывается
диаметром.
Уравнение
диаметра, сопряженного с неасимп­тотическим
направлением вектора с(с
,
c₂),
имеет
вид

(а₁₁с

+
а₁₂с₂)x′

+
(а₁₂с₁
+
а₂₂с₂)х₂
+
a₁c₁
+ а₂с₂
= 0.
(2)

Как
отмечалось в предыдущем параграфе,
каждый диаметр линии (1)
проходи!
через любой ее центр. Для линии (1),
имеющей прямую центров,
вопрос о диаметрах решается теперь
полностью: у такой линии имеется только
один диаметр — прямая центров.

Рассмотрим
теперь вопрос о диаметрах центральной
линии (1). В этом случае

а₁₁а₂₂
— а

≠ 0.
(3)

Определение
8.1.
Два
направления c
:с₂
и
c′
:с′₂
называются сопряженными
относительно центральной линии второго
порядка (1), если
они удовлетворяют соотношению
а₁₁с
c′

+
а₁₂
(с
₁c
′
+
с₂с′
)
+
а₂₂с₂с′₂
=
0. (4)

Отметим
основные свойства сопряженных направлений.

1. Каждому
направлению c
:с₂
соответствует
в качестве сопря­

женного
одно вполне определенное направление
c′
:с′₂.

► В
самом деле, перепишем равенство (4) в
виде

(а₁₁с

+
а₁₂с₂)c′

+(
а₁₂с₁
+
а₂₂с₂с₂
)
c′
=
0.
(5)

Е
сли
предположить, что а₁₁
c₁
+ a₁₂c₂
=
0,

(6)

a_l2c₁
+ a₂₂c₂
= 0.

то
в силу неравенства (3) мы получим, что
система уравнений (6) относительно
неизвестных c

и
с₂
имеет
только нулевое решение: c

= 0, с₂
=
0. Но это невозможно, так как вектор
с(c
,с₂)—ненуле­вой.
Итак, оба коэффициента при c

и
с₂
в уравнении (5) не могут одновременно
обратиться в нуль, и, следовательно, из
уравнения мы найдем
вполне определенное отношение
c′

:
с′_2.◄

2. Асимптотическое
направление, и только оно, сопряжено

самому
себе.

► В
самом деле, если для данного направления
c

:
с₂
сопряженным

является
само это направление, то равенство (4)
дает а₁₁с
²
+ 2а₁₂с₁с₂
+ а₂₂с

= 0
(7)

т.
е. направление c
:
с₂
—
асимптотическое.

Обратно,
если направление c
:
с₂
—
асимптотическое, т. е. удов­летворяет
равенству (7),
то равенство (4) выполняется, если
c′
=
c

и
с’₂
== с₂.
Следовательно,
направление c
:
с₂
сопряжено
само­му
себе. ◄

3.
Если
направление c
:с₂
—
неасимптотическое,
то сопряженное направление
также неасимптотическое и является
направлением диаметра,
сопряженного с направлением c
:с₂.

►В
самом деле, диаметр, сопряженный с
неасимптотическим на­правлением
c
:
с₂,—
это прямая (2).
Для направляющего вектора с'(с’,
с₂)
этой
прямой выполняется условие с′
:
с’₂=
— (a_l2
c

+
a₂₂c₂):(a₁₁
c

+
a₁₂c₂),
откуда
и следует равенство (5).◄

Определение
8.2.
Два
диаметра линии второго порядка, имеющие
взаимно сопряженные направления,
называются сопряжен­ными
диаметрами.

Из
определения диаметра следует, что каждый
из двух сопряжен­ных
диаметров делит пополам все хорды,
параллельные другому диаметру.

На
рис. 8.1 изображены эллипс, два его взаимно
сопряженных диаметра
и параллельные им хорды.

Мы знаем,
что любой диаметр центральной линии
второго

порядка
(1) проходит через ее центр. По­кажем
теперь, что

любая
прямая l
неасимптотиче­ского
направления, проходящая рис.
8.1

через
центр цен­тральной линии второго
порядка, является диамет­ром
этой линии. В самом деле, пусть c

:
с₂
определяет
направление
прямой / и c
:с₂—
сопряженное на­правление,
причем оба этих направления
являются неасимпто­тическими.
Рассмотрим диаметр, сопряженной с
направлением c
:
с₂.
Он
имеет направление c
:
с₂
и,
проходя через центр ли­нии
(1), совпадает с прямой l.

Теперь
рассмотрим диаметры параболы. Пусть
парабола в неко­торой
ортонормированной системе координат
задается уравнением 2рх₁
—
х²₂
= 0.
(8)

Уравнение
диаметра параболы (8),
сопряженного с направле­нием
c
:
с₂,
имеет
вид р
c
—
с₂х₂
= 0. Отсюда
следует, что все ди­аметры
параболы параллельны ее оси и любая
прямая, параллельная оси параболы,
является диаметром.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #