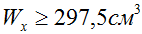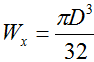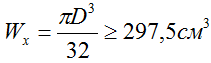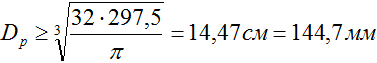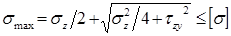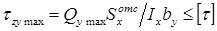Пример решения задачи по подбору минимального диаметра балки круглого поперечного сечения, обеспечивающего её прочность.
Задача
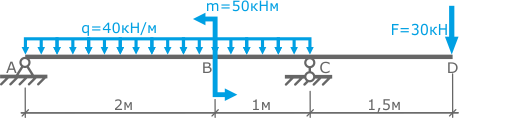
Для заданной стальной балки рассчитать диаметр поперечного сечения по условию прочности.
Полученный размер принять согласно ГОСТ 6636. Допустимые напряжения [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов.
- Расчет момента сопротивления сечения балки по условию прочности.
В предыдущем пункте была рассчитана величина минимально необходимого момента сопротивления сечения балки
С другой стороны момент сопротивления круглого сечения определяется по формуле
таким образом
откуда, расчетный диаметр
Отметим что полученный размер это минимально необходимый диаметр балки, обеспечивающий ее прочность.
Если нет дополнительных условий, то полученный размер можно округлить до целого значения в миллиметрах – 145мм. Округление выполняется исключительно в большую сторону.
По ГОСТ 6636 ближайшее значение в сторону увеличения также составляет 145 мм, его и принимаем за окончательный диаметр балки, т.е. D=145мм.
Оценка экономичности сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Обычно в инженерной
практике проверку прочности балок
производят по нормальным наибольшим и
касательным напряжениям [2]. Нормальные
напряжения σ зависят от величины
изгибавшего момента, а касательные
τ – от величины поперечной силы.
Касательные напряжения в сечениях балки
обычно не играют существенной роли,
поэтому размеры сечения балок определяют
из условия прочности по нормальным
максимальным напряжениям:

где Мmax
–
наибольший (по абсолютной величине)
изгибающий момент, известный из эпюры
изгибающих моментов ().
Сечение балки
подбирается по моменту сопротивления
относительно нейтральной оси:

(3.10)
Для балки
прямоугольного сечения
.
Числовые значения
моментов сопротивления стандартных
профилей проката указаны в соответствующих
государственных стандартах на прокат,
а на балки двутавровые приведены в
таблицах приложения Г. Следует подбирать
номер профиля, имеющий большее стандартное
ближайшее значение. Допустимо принимать
и меньшее ближайшее значение WхСТ,
однако оно должно удовлетворять условию:
.
Момент сопротивления
при изгибе
Подходит швеллер
№ 8 (Wx=22,4
см3,
площадь сечения А=8,98 см2).
Определим
прямоугольное сечение (рисунок 3.10) при
Рисунок 3.10 –
Сечение швеллера и прямоугольное сечение
Площадь
прямоугольного сечения
A=bh=16,27
см2
≈
в 2 раза больше площади швеллера.
3.4 Совместное действие изгиба и кручения
Сочетание деформаций
изгиба и кручения испытывает большинство
валов, которые обычно представляют
собой прямые брусья круглого или
кольцевого сечения.
Возникающие от
изгиба нормальные напряжения достигают
максимального значения в волокнах,
наиболее удаленных от нейтральной оси:
,
где М – максимальный
изгибающий момент, Нм;
W
– осевой момент сопротивления сечения,
м3.
Для вала круглого
сечения
Максимальные
касательные напряжения при кручении
возникают в точках контура поперечного
сечения:
где Wp
– полярный момент сопротивления сечения
(Wp=2W),
м3;
Т
– крутящий момент, Нм.
Таким образом, при
сочетании изгиба и кручения опасными
будут точки (для конкретного поперечного
сечения), наиболее удаленные от нейтральной
оси.
Применив третью
теорию прочности, получим

Расчетная формула
для круглых валов принимает вид:

где М
экв.
– эквивалентный момент, Нм;
[σ]
– допускаемое
напряжение на растяжение для материала
вала, Па.
Если величина и
направление нагрузки во время работы
вращающегося вала остаются неизменными,
то напряжения изгиба в теле вала будут
изменяться во времени по симметричному
циклу – I циклу
нагружения (рисунок 3.11).
Рисунок 3.11 – График
изменения во времени напряжения изгиба
I
цикл
При действии на
вал нагрузок в разных плоскостях силы
раскладывают на две взаимно перпендикулярные
плоскости, за одну из которых выбирают
плоскость действия одной из сил.
Суммарный изгибающий
момент определится как геометрическая
сумма моментов, действующих во взаимно
перпендикулярных плоскостях
рассматриваемого сечения:
где Мiв
и Мiгор
– изгибающие
моменты в i
– м сечении,
действующие в вертикальной и в
горизонтальной плоскостях соответственно.
Эквивалентный
момент определится по формуле:
,
Диаметр вала в
опасном сечении
рассчитывается из условия прочности:

Примечание –
При решении задач все необходимые
вычисления следует сначала проделать
в общем виде, обозначая все данные и
искомые величины буквами, после чего
вместо буквенных обозначений подставить
их числовые значения и найти результат.
На расчетных эскизах размеры должны
быть проставлены теми же буквами, какие
имеются в расчетных формулах.
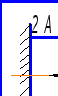
Пример 4.
Построить
эпюры изгибающих, крутящего, суммарного
изгибающего моментов и определить
диаметр вала (рисунок 3.12) в опасном
сечении.
Т = 0,2 кНм, F
= 2 кН, q
= 4 кН/м, a
= 0,2м, b
=1,2а = 0,24м,
с = 0,8а = 0,16м, [σ]
= 110МПа.
Решение:
Плоскость yz:
Плоскость хz:
Из условия прочности
наиболее нагруженного сечения А определим
диаметр вала.
Рисунок 3.12 –
Расчетная
схема и эпюры вала
ПРИЛОЖЕНИЕ А
ЗАДАЧА 1
Расчет бруса на
осевое растяжение (сжатие)
Сечение бруса
квадратное. Материал – сталь. Допускаемое
напряжение [σ]
= 100 МПа. Модуль продольной упругости Е
= 2·105
МПа. Исходные данные к расчету см. в
таблице + рисунок.
ИСХОДНЫЕ ДАННЫЕ
|
Вариант |
F1 |
F2 |
F3 |
l1 |
l2 |
l3 |
|
кН |
м |
|||||
|
1 |
32 |
18 |
24 |
0,7 |
0,4 |
0,8 |
|
2 |
28 |
16 |
12 |
0,6 |
0,5 |
0,7 |
|
3 |
22 |
8 |
26 |
0,5 |
0,6 |
0,9 |
|
4 |
19 |
24 |
15 |
0,8 |
0,6 |
0,5 |
|
5 |
30 |
12 |
16 |
0,4 |
0,9 |
0,6 |
|
6 |
27 |
15 |
10 |
0,6 |
0,7 |
0,8 |
|
7 |
24 |
14 |
8 |
0,3 |
0,8 |
0,7 |
|
8 |
26 |
16 |
11 |
0,7 |
0,9 |
0,4 |
|
9 |
25 |
12 |
18 |
0,5 |
0,5 |
0,9 |
|
10 |
31 |
26 |
14 |
0,7 |
0,3 |
0,5 |
|
11 |
18 |
15 |
12 |
0,6 |
0,6 |
0,8 |
|
12 |
23 |
25 |
12 |
0,8 |
0,4 |
0,7 |
|
13 |
16 |
8 |
12 |
0,4 |
0,7 |
0,9 |
|
14 |
18 |
10 |
14 |
0,6 |
0,5 |
0,8 |
|
15 |
22 |
12 |
14 |
0,5 |
0,6 |
0,7 |
|
16 |
20 |
9 |
12 |
0,7 |
0,4 |
0,8 |
|
17 |
24 |
16 |
12 |
0,9 |
0,3 |
0,6 |
|
18 |
18 |
10 |
14 |
0,8 |
0,2 |
0,7 |
|
19 |
25 |
18 |
14 |
0,7 |
0,6 |
0,9 |
|
20 |
19 |
11 |
10 |
0,8 |
0,5 |
0,6 |
|
21 |
30 |
13 |
10 |
0,4 |
0,8 |
0,5 |
|
22 |
27 |
15 |
12 |
0,6 |
0,9 |
0,4 |
|
23 |
22 |
11 |
10 |
0,7 |
0,7 |
0,6 |
|
24 |
20 |
9 |
10 |
0,5 |
0,9 |
0,7 |
|
25 |
24 |
12 |
14 |
0,7 |
0,4 |
0,9 |
|
26 |
19 |
10 |
11 |
0,8 |
0,3 |
0,6 |
|
27 |
25 |
13 |
13 |
0,4 |
0,7 |
0,8 |
|
28 |
21 |
16 |
12 |
0,5 |
0,5 |
0,7 |
|
29 |
22 |
20 |
10 |
0,8 |
0,6 |
0,8 |
|
30 |
23 |
15 |
11 |
0,7 |
0,3 |
0,9 |
Расчетные схемы
ПРИЛОЖЕНИЕ Б
ЗАДАЧА 2 РАСЧЕТ
ВАЛА НА КРУЧЕНИЕ
Сечение вала
круглое, сплошное и кольцевое. Допускаемое
напряжение кручения [τ]=25
МПа. Модуль сдвига G=8∙104
МПа
|
Вариант |
Т1, |
Т2, |
Т3, |
Т4, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
200 |
300 |
400 |
0,8 |
0,7 |
0,4 |
0,6 |
0,3 |
|
|
2 |
300 |
500 |
500 |
0,7 |
0,6 |
0,5 |
0,8 |
0,4 |
|
|
3 |
400 |
400 |
300 |
0,9 |
0,5 |
0,6 |
0,3 |
0,2 |
|
|
4 |
100 |
200 |
300 |
0,5 |
0,8 |
0,9 |
0,4 |
0,3 |
|
|
5 |
300 |
400 |
100 |
0,6 |
0,4 |
0,6 |
0,5 |
0,4 |
|
|
6 |
100 |
100 |
500 |
0,8 |
0,6 |
0,7 |
0,3 |
0,2 |
|
|
7 |
300 |
200 |
200 |
0,7 |
0,3 |
0,8 |
0,4 |
0,3 |
|
|
8 |
500 |
600 |
500 |
0,4 |
0,7 |
0,9 |
0,5 |
0,4 |
|
|
9 |
600 |
800 |
700 |
0,9 |
0,5 |
0,5 |
0,3 |
0,2 |
|
|
10 |
400 |
200 |
300 |
0,5 |
0,7 |
0,8 |
0,2 |
0,3 |
|
|
11 |
300 |
500 |
600 |
0,8 |
0,6 |
0,6 |
0,4 |
0,3 |
|
|
12 |
100 |
200 |
200 |
0,7 |
0,8 |
0,4 |
0,3 |
0,4 |
|
|
13 |
700 |
500 |
200 |
0,9 |
0,4 |
0,7 |
0,2 |
0,3 |
|
|
14 |
800 |
400 |
300 |
0,8 |
0,6 |
0,5 |
0,3 |
0,3 |
|
|
15 |
900 |
600 |
400 |
0,7 |
0,5 |
0,6 |
0,4 |
0,4 |
|
|
16 |
100 |
200 |
300 |
0,8 |
0,7 |
0,4 |
0,2 |
0,5 |
|
|
17 |
200 |
800 |
100 |
0,6 |
0,9 |
0,3 |
0,3 |
0,6 |
|
|
18 |
300 |
800 |
100 |
0,7 |
0,8 |
0,2 |
0,4 |
0,7 |
|
|
19 |
400 |
500 |
300 |
200 |
0,9 |
0,7 |
0,6 |
0,2 |
|
|
20 |
500 |
500 |
200 |
300 |
0,6 |
0,8 |
0,5 |
0,3 |
|
|
21 |
600 |
900 |
400 |
100 |
0,5 |
0,4 |
0,8 |
0,4 |
|
|
22 |
700 |
800 |
300 |
200 |
0,4 |
0,6 |
0,9 |
0,2 |
|
|
23 |
800 |
700 |
100 |
400 |
0,6 |
0,7 |
0,7 |
0,3 |
|
|
24 |
900 |
600 |
200 |
300 |
0,7 |
0,5 |
0,9 |
0,4 |
|
|
25 |
100 |
500 |
300 |
200 |
0,9 |
0,7 |
0,4 |
0,2 |
|
|
26 |
200 |
300 |
500 |
300 |
0,6 |
0,8 |
0,3 |
0,4 |
|
|
27 |
300 |
300 |
400 |
200 |
0,8 |
0,4 |
0,7 |
0,3 |
|
|
28 |
400 |
200 |
600 |
100 |
0,7 |
0,5 |
0,5 |
0,2 |
|
|
29 |
500 |
100 |
700 |
200 |
0,8 |
0,8 |
0,6 |
0,3 |
|
|
30 |
600 |
200 |
800 |
300 |
0,9 |
0,7 |
0,3 |
0,4 |
Расчетные схемы
ПРИЛОЖЕНИЕ В
ЗАДАЧА 3
РАСЧЕТ НА ПРОЧНОСТЬ ДВУХОПОРНОЙ БАЛКИ
ПРИ ИЗГИБЕ
Для данной балки подобрать сечения
двутавра и прямоугольника (h/b=2).
Допускаемое напряжения изгиба [σ]=160
МПа
|
Вариант |
М,K |
F, |
q, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
18 |
26 |
14 |
2 |
2 |
5 |
1 |
1 |
|
2 |
24 |
18 |
10 |
2 |
3 |
2 |
3 |
2 |
|
3 |
16 |
34 |
12 |
2 |
3 |
3 |
2 |
2 |
|
4 |
30 |
24 |
16 |
2 |
4 |
4 |
1 |
2 |
|
5 |
20 |
12 |
8 |
1,8 |
2,2 |
1 |
5 |
1 |
|
6 |
22 |
16 |
10 |
1,6 |
1 |
1,4 |
6 |
2 |
|
7 |
18 |
22 |
14 |
2,2 |
2 |
1,8 |
5 |
1 |
|
8 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
9 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
10 |
14 |
15 |
8 |
1,6 |
2 |
1,4 |
4 |
3 |
|
11 |
10 |
23 |
12 |
2 |
2 |
2 |
4 |
2 |
|
12 |
18 |
17 |
10 |
1,8 |
3 |
1,2 |
5 |
1 |
|
13 |
16 |
25 |
15 |
2 |
2 |
4 |
2 |
2 |
|
14 |
24 |
16 |
10 |
2 |
3 |
4 |
2 |
1 |
|
15 |
1 |
22 |
12 |
1,6 |
2,4 |
3,5 |
2,5 |
2 |
|
16 |
20 |
18 |
14 |
1,8 |
2,2 |
4,5 |
2,5 |
2 |
|
17 |
22 |
24 |
8 |
2 |
2 |
4 |
3 |
1 |
|
18 |
16 |
26 |
6 |
2 |
2 |
3,5 |
3,5 |
1 |
|
19 |
18 |
20 |
10 |
1,5 |
2,5 |
4,2 |
1,8 |
8 |
|
20 |
28 |
18 |
16 |
1,8 |
2,2 |
4,5 |
2,5 |
3 |
|
21 |
17 |
25 |
12 |
2 |
2 |
1 |
5 |
2 |
|
22 |
15 |
30 |
10 |
1,5 |
2,5 |
2 |
4 |
1 |
|
23 |
26 |
22 |
8 |
2 |
2 |
2 |
3 |
2 |
|
24 |
30 |
18 |
14 |
1,6 |
3,0 |
2 |
4 |
1 |
|
25 |
24 |
26 |
15 |
1,5 |
2,5 |
6 |
1 |
1 |
|
26 |
22 |
13 |
2,5 |
1,5 |
5 |
2 |
2 |
|
|
27 |
20 |
12 |
2,0 |
1,5 |
5,5 |
3 |
2 |
|
|
28 |
18 |
28 |
10 |
2,0 |
1,5 |
4,5 |
2 |
2 |
|
29 |
30 |
20 |
8 |
1,8 |
3,2 |
1 |
2 |
1 |
|
30 |
28 |
18 |
15 |
2 |
2,5 |
1,5 |
5 |
2 |
Расчетные схемы
задачи 3
ПРИЛОЖЕНИЕ Г
Сталь прокатная
– балки двутавровые (ГОСТ 8239-83)
h
– высота профиля;
b
– ширина;
d
– толщина;
t
– средняя толщина;
R
и r
– внутренний и наружный радиусы
скруглений;
J
– момент инерции;
W
– момент сопротивления;
i
– радиус инерции;
S
– статический момент полусечения
|
Номер профиля |
Масса |
Размеры, |
Площадь сечения, |
Jx, см4 |
Wx, см3 |
ix, см |
Sx, см3 |
Jy, см4 |
Wy, см3 |
iy, см |
|||||
|
h |
b |
d |
t |
R |
r |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
10 |
9,46 |
100 |
55 |
4,5 |
7,2 |
7 |
2,5 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
11,45 |
120 |
64 |
4,8 |
7,3 |
7,5 |
3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
13,7 |
140 |
73 |
4,9 |
7,5 |
8 |
3 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
15,9 |
160 |
81 |
5,0 |
7,8 |
8,5 |
3,5 |
20,2 |
873 |
109,0 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
18,4 |
180 |
90 |
5,1 |
8,1 |
9,0 |
3,5 |
23,4 |
1290 |
143,0 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
18а |
19,9 |
180 |
100 |
5,1 |
8,3 |
9,0 |
3,5 |
25,4 |
1430 |
159,0 |
7,51 |
89,8 |
114,0 |
22,8 |
2,12 |
|
20 |
21,0 |
200 |
100 |
5,2 |
8,4 |
9,5 |
4,0 |
26,8 |
1840 |
184,0 |
8,28 |
104,0 |
115,0 |
23,1 |
2,07 |
|
20а |
22,7 |
200 |
110 |
5,2 |
8,6 |
9,5 |
4,0 |
28,9 |
2030 |
203,0 |
8,37 |
114,0 |
155,0 |
28,2 |
2,32 |
|
22 |
24,0 |
220 |
110 |
5,4 |
8,7 |
10,0 |
4,0 |
30,6 |
2550 |
232,0 |
9,13 |
131,0 |
157,0 |
28,6 |
2,27 |
|
22а |
25,8 |
220 |
120 |
5,4 |
8,9 |
10,0 |
4,0 |
32,6 |
2790 |
254,0 |
9,22 |
143,0 |
106,0 |
34,3 |
2,5 |
|
24 |
27,3 |
240 |
115 |
5,6 |
9,5 |
10,5 |
4,0 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
24а |
29,4 |
240 |
125 |
5,6 |
9,8 |
20,5 |
4,0 |
37,5 |
3800 |
317 |
10,1 |
178 |
260 |
41,6 |
2,63 |
|
27 |
31,5 |
270 |
125 |
6,0 |
9,8 |
11,0 |
4,5 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
27а |
33,9 |
270 |
135 |
6,0 |
10,2 |
11,0 |
4,5 |
43,2 |
5500 |
407 |
11,3 |
229 |
337 |
50,0 |
2,8 |
|
30 |
36,5 |
300 |
135 |
6,5 |
10,2 |
12,0 |
5 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
30а |
39,2 |
300 |
145 |
6,5 |
10,7 |
12,0 |
5 |
49,9 |
7780 |
518 |
12,5 |
292 |
436 |
60,1 |
2,95 |
|
33 |
42,2 |
330 |
140 |
7,0 |
11,2 |
13,0 |
5 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,1 |
3,79 |
|
36 |
48,6 |
360 |
145 |
7,5 |
12,3 |
14,0 |
6 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
57,0 |
400 |
155 |
8,3 |
13,0 |
15,0 |
6 |
72,6 |
19062 |
953 |
16,2 |
545 |
667 |
86,1 |
3,08 |
|
45 |
66,5 |
450 |
160 |
9,0 |
14,2 |
16,0 |
7 |
84,7 |
27696 |
1231 |
18,1 |
708 |
808 |
101,0 |
3,09 |
|
50 |
78,5 |
500 |
170 |
10,0 |
15,2 |
17,0 |
7 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123,0 |
3,23 |
|
60 |
108,0 |
600 |
190 |
12,0 |
17,8 |
20,0 |
8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182,0 |
3,54 |
|
60б |
120,0 |
650 |
200 |
12,0 |
19,2 |
22,0 |
9 |
153 |
101400 |
3120 |
25,8 |
1800 |
2170 |
217,0 |
3,77 |
|
70 |
138,0 |
700 |
210 |
13,0 |
20,8 |
24,0 |
10 |
176 |
134600 |
3840 |
27,7 |
2230 |
2730 |
260,0 |
3,94 |
|
70а |
168,0 |
700 |
210 |
15,0 |
24,0 |
24,0 |
10 |
202 |
152700 |
4360 |
27,5 |
2550 |
3240 |
309,0 |
4,01 |
|
70б |
184,0 |
700 |
210 |
17,5 |
28,2 |
24,0 |
10 |
234 |
175770 |
5010 |
27,4 |
2940 |
3910 |
373,0 |
4,09 |
ПРИЛОЖЕНИЕ Д
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет балки, подбор прямоугольного сечения

Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
ΣFx = 0: HA = 0
ΣMA = 0: Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке A:
- q1*3*(3/2) + RB*3 - M1 + P1*4.5 = 0
ΣMB = 0: Найдем сумму моментов относительно шарнирно-подвижной опоры в точке B:
- RA*3 + q1*3*(3 - 3/2) - M1 + P1*1.5 = 0
2. Решаем полученную систему уравнений, находим неизвестные :
HA = 0 (кН)
3. Вычислим реакцию шарнирно-подвижной опоры в точке B
RB = ( q1*3*(3/2) + M1 - P1*4.5) / 3 = ( 40*3*(3/2) + 30 - 10*4.5) / 3 = 55.00 (кН)
4. Вычислим реакцию шарнирно-неподвижной опоры в точке A
RA = ( q1*3*(3 - 3/2) - M1 + P1*1.5) / 3 = ( 40*3*(3 - 3/2) - 30 + 10*1.5) / 3 = 55.00 (кН)
5. Выполним проверку ΣFy = 0: RA - q1*3 + RB + P1 = 55.00 - 40*3 + 55.00 + 10 = 0
Построение эпюр
Рассмотрим 1-й участок 0 ≤ x1 < 3
Поперечная сила Q:
Q(x1) = + RA - q1*(x1 - 0)
Значения Q на краях участка:
Q1(0) = + 55 - 40*0 = 55 (кН)
Q1(3) = + 55 - 40*3 = -65 (кН)На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения:
x = 1.38
Изгибающий момент M:
M(x1) = + RA*(x1) - q1*(x1)2/2
Значения M на краях участка:
M1(0) = + 55*(0) - 40*02/2 = 0 (кН*м)
M1(3) = + 55*(3) - 40*32/2 = -15 (кН*м)Локальный экстремум в точке x = 1.38:
M1(1.38) = + 55*(1.38) - 40*(1.38 - 0)2/2 = 37.81 (кН*м)
Рассмотрим 2-й участок 3 ≤ x2 < 4
Поперечная сила Q:
Q(x2) = + RA - q1*3 + RB
Значения Q на краях участка:
Q2(3) = + 55 - 40*3 + 55 = -10 (кН)
Q2(4) = + 55 - 40*3 + 55 = -10 (кН)
Изгибающий момент M:
M(x2) = + RA*(x2) - q1*3*[(x2 - 3) + 3/2] + RB*(x2 - 3)
Значения M на краях участка:
M2(3) = + 55*(3) - 40*3*(0 + 1.50) + 55*(3 - 3) = -15 (кН*м)
M2(4) = + 55*(4) - 40*3*(1 + 1.50) + 55*(4 - 3) = -25 (кН*м)
Рассмотрим 3-й участок 4 ≤ x3 < 4.5
Поперечная сила Q:
Q(x3) = + RA - q1*3 + RB
Значения Q на краях участка:
Q3(4) = + 55 - 40*3 + 55 = -10 (кН)
Q3(4.50) = + 55 - 40*3 + 55 = -10 (кН)
Изгибающий момент M:
M(x3) = + RA*(x3) - q1*3*[(x3 - 3) + 3/2] + RB*(x3 - 3) + M1
Значения M на краях участка:
M3(4) = + 55*(4) - 40*3*(1 + 1.50) + 55*(4 - 3) + 30 = 5 (кН*м)
M3(4.50) = + 55*(4.50) - 40*3*(1.50 + 1.50) + 55*(4.50 - 3) + 30 = 0 (кН*м)
Подбор сечения
Прямоугольное сечение балки подбираем из условия прочности при допускаемом напряжении: 





Момент сопротивления прямоугольного сечения определим по формуле:
Требуемый момент сопротивления 
Поскольку дано соотношение сторон
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки. Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=145 (мм), b=75 (мм)
Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.RU
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.
Решение
а) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
Тогда:
б) Проверка прочности:
— по условию прочности нормальных напряжений:
— по условию прочности касательных напряжений:
Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

Тогда


Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.
Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда
Iучасток
∑М(С) = М(z1) +F·z1=0,
ММ(z1) = –F·z1= — 30 ·z1 —
– уравнение прямой.
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок
откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условиянаходим
:

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм

а) сечение круглой формы d=?
б) сечение прямоугольной формы при h/b = 2:

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:
Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения
— для прямоугольного сечения
Воспользуемся этими формулами. Тогда
— для балки круглого сечения при :
— для балки прямоугольного сечения
Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.
Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.
∑М(С) = М(z1) – М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок

Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.
III участок

Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок

z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :
В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:


Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:

Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :
Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение
1.Определение опорных реакций
∑М(А) = F · 2 + М1 – М2— q·6·7 + В · 8 =0,

∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок
∑М(С) = М(z1) + F·z1=0,
М(z1) = – F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= – F— Q(z1) = 0,
Q(z1) = — 20кН.
II участок
z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок

Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,
IV участок

Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)
Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:
Вариант 2. Деревянное круглое
Принимаем d=0,45м,
Проверяем по τ:
Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)
Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:
b(у)= b — d= 0,19 — 0,076 = 0,114м
Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).

по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:
Вариант 5. Сталь, круглая труба
Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:
Вариант 6. Сталь, прямоугольная труба
b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,
Принимаем b=0,13м, h=0,26м.
Проверка по τ:
Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба –
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
Проверка прочности балки и подбор поперечных сечений
Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре 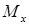
Условие прочности при изгибе по нормальным напряжениям: 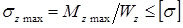
где допускаемое напряжение 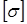
Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: 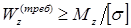
При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон 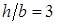
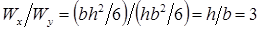
Проверка прочности двутавров
Для тонкостенных балок, например балок двутаврового профиля, проверка прочности производится следующим образом:
в наиболее удаленных от нейтральной оси точках прочность проверяется по формуле 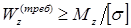
в точках, где полка соединяется со стенкой прочность определяется по главным напряжениям.
в точках, расположенных на нейтральной оси, прочность определяется по наибольшим касательным напряжениям: