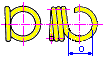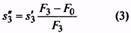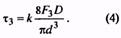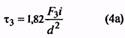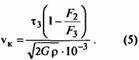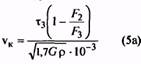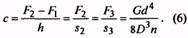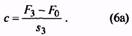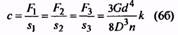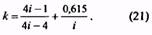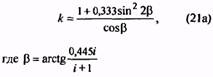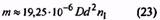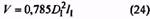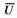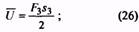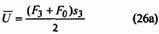Основные
понятия
Пружина
растяжения — это спирально-цилиндрическая
пружина, витки которой прилегают друг
к другу. Пружина подвергается действию
противоположно направленных усилий,
приложенных вдоль ее оси.
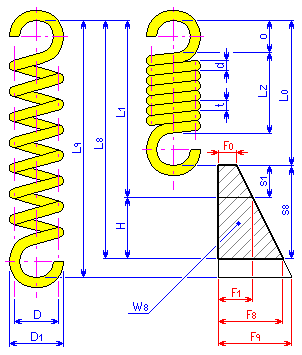
Размеры
|
d |
диаметр |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
H |
рабочая |
|
t |
шаг |
|
o |
высота |
|
sx |
деформация |
|
Lx |
длина |
|
Fx |
рабочая |
|
W8 |
энергия |
|
x |
индекс, |
Навивка
-
Вправо
(стандарт) -
Влево
(должна отображаться соответствующая
надпись)
Состояния
-
Свободное:
пружина не нагружена (индекс 0) -
Предварительная
нагрузка: пружина с минимальной рабочей
нагрузкой (индекс 1) -
Полная
нагрузка: пружина с максимальной рабочей
нагрузкой (индекс 8) -
Предел:
пружина вдавлена до касания витков
(индекс 9).
Зацепы
пружин растяжения
Высота
зацепа пружины растяжения
Где:
|
L0 |
длина |
|
LZ |
длина |
Часто
используемые зацепы пружин растяжения
|
Тип |
Изображение |
|
Половина |
|
|
Обычно |
|
|
Полный |
|
|
Используется |
|
|
Полный |
|
|
Когда |
|
|
Полный |
|
|
Обычно |
|
|
Поднятый |
|
|
Обычно |
|
|
Два |
|
|
Используется |
|
|
Два |
|
|
Когда |
Расчет
пружин в метрических единицах
Общие
формулы расчета
Коэффициент
использования материала
Наружный
диаметр пружины
D1 =
D + d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Внутренний
диаметр пружины
D2 =
D – d [мм]
Где:
|
D |
средний |
|
|
d |
диаметр |
Рабочая
деформация
H
= L81=
s81[мм]
Где:
|
L8 |
длина |
|
|
L1 |
длина |
|
|
s8 |
деформация |
|
|
s1 |
деформация |
Высота
зацепа пружины
Где:
|
L0 |
длина |
|
|
LZ |
длина |
Индекс
пружины
c
= D/d [-]
Где:
|
D |
средний |
|
|
d |
диаметр |
Поправочный
коэффициент Валя
Где:
|
c |
индекс |
|
|
LZ |
длина |
Начальное
растяжение
Где:
|
d |
диаметр |
|
|
0 |
напряжение |
|
|
D |
средний |
|
|
Kw |
поправочный |
Общая
сила, действующая в пружине
Где:
|
d |
диаметр |
|
|
G |
напряжение |
|
|
D |
средний |
|
|
Kw |
поправочный |
|
|
G |
модуль |
Жесткость
пружины
Где:
|
d |
диаметр |
|
|
G |
модуль |
|
|
D |
средний |
|
|
n |
количество |
|
|
F8 |
рабочее |
|
|
F1 |
рабочее |
|
|
H |
рабочая |
Расчет
конструкции пружины
При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для
заданной нагрузки, материала и сборочных
размеров.
Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для данного напряжения 0 согласно
формуле, расчет пружины повторяется с
использованием скорректированного
значения напряжения в свободном состоянии
из рекомендуемого диапазона.
Пружине
без начального растяжения соответствует
средний рекомендуемый шаг витков t =
0,35 D [мм].
Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для выбранного шага, расчет пружины
повторяется с использованием
скорректированного значения шага из
рекомендуемого диапазона 0,3 D ≤ t ≤ 0,4
D [мм].
Конструкция
пружины определяется с учетом условия
прочности 8≤ usA и
рекомендуемых диапазонов некоторых
геометрических параметров пружины:
L0≤ D
и L0≤ 31,5
д и 4 ≤ D/d ≤16 и n 2.
Задание
нагрузки, материала и сборочных размеров
пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем
вычисляется длина пружины в свободном
состоянии.
После
расчета выбирается диаметр проволоки,
количество витков и диаметры пружины
– так, чтобы высота зацепа соответствовала
выбранному типу зацепа. Кроме того,
должны выполняться упомянутые выше
прочностные и геометрические условия.
Конструкция пружины должна удовлетворять
по диаметрам всем заданным начальным
условиям. При отсутствии таких
дополнительных условий предельный
диаметр пружины устанавливается по
геометрическим условиям для
минимально/максимально допустимого
диаметра проволоки.
Отбираются
все диаметры проволоки (от меньшего к
большему), которые проходят по прочностным
и геометрическим условиям. Проверяются
высота зацепа и количество витков. Если
все условия выполнены, расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Комбинация
диаметра проволоки, количества витков
и диаметра пружины должна давать в итоге
такую высоту зацепа, которая удовлетворяет
его типу. Вначале в качестве типа зацепа
берется полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание
нагрузки, материала и диаметра пружины
Вначале
выполняется проверка входных величин
для расчета.
После
проверки выбирается диаметр проволоки,
количество витков, длина пружины в
свободном состоянии и сборочные размеры
пружины – так, чтобы высота зацепа
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия. Если сборочный
размер L1 или
L8 взят
из спецификации или значение рабочей
деформации пружины ограничено, конструкция
пружины должна соответствовать этому
условию. В остальных случаях предельные
значения сборочных размеров пружины и
ее длины в свободном состоянии определяются
геометрическими условиями для заданного
диаметра пружины и минимального/максимального
допустимого диаметра проволоки.
Формула
для проектирования пружины по заданному
диаметру проволоки.
где
значение 8 =
0,85 A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Для
высоты, вычисленной таким способом,
выбирается соответствующий тип зацепа.
Комбинация диаметра проволоки, количества
витков, длины пружины в свободном
состоянии и сборочных размеров пружины
должна давать в итоге такую высоту
зацепа, которая удовлетворяет его типу.
Вначале в качестве типа зацепа берется
полный виток, затем, если он не
годится–полный виток внутри и т.д.
Задание
максимального рабочего усилия, материала,
сборочных размеров и диаметра пружины
Вначале
выполняется проверка входных величин
для расчета.
Затем
подбирается диаметр проволоки, количество
витков, длина свободной пружины и
минимальное рабочее усилие F1 таким
образом, чтобы высота зацепа пружины
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия.
Формула
для проектирования пружины по заданному
диаметру проволоки.
где
значение 8 =
0,9 A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.
Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.
Проверочный
расчет пружины
Расчет
соответствующих значений сборочных
размеров и рабочего отклонения для
указанной нагрузки, материала и размеров
пружины.
Сначала
проверяются расчетные входные значения.
Затем на основании приведенных ниже
формул вычисляются сборочные размеры.
Длина
предварительно нагруженной пружины
Длина
полностью нагруженной пружины
Где:
|
L0 |
длина |
|
|
F1 |
рабочая |
|
|
D |
средний |
|
|
n |
количество |
|
|
G |
модуль |
|
|
d |
диаметр |
|
|
F8 |
рабочее |
Рабочая
деформация
H
= L18[мм]
Расчет
рабочих сил
Расчет
соответствующих сил, действующих в
пружинах в рабочем состоянии для
указанного материала, сборочных размеров
и размеров пружины. Сначала проверяются
и рассчитываются входные данные, а затем
выполняется расчет рабочих сил с помощью
следующих формул.
Минимальное
рабочее усилие
Максимальное
рабочее усилие
Расчет
выходных параметров пружины
Эта
часть является общей для всех типов
расчета пружины. Расчет производится
в следующем порядке.
Коэффициент
высоты зацепа
Жесткость
пружины
Длина
части с витками
|
Пружина |
|
|
Lz = |
|
|
Пружина |
|
|
Lz = |
Деформация
предварительно нагруженной пружины
s1 =
L1 –
L0 [мм]
Полная
деформация пружины
s8 =
L8 –
L0 [мм]
Напряжение
при кручении материала пружины в
состоянии предварительной нагрузки
Напряжение
материала пружины при кручении при
полном нагружении
Предельное
усилие в пружине
Деформация
в предельном состоянии
Где:
|
k |
жесткость |
|
|
F9 |
рабочее |
|
|
F0 |
начальное |
Предельная
длина пружины
L9 =
L0 +
s9 [мм]
Энергия
деформации пружины
Длина
развернутой проволоки
|
l |
|||
|
Где |
|||
|
для |
|||
|
l0 = D |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = D |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
|||
|
для |
|||
|
l0 = |
Масса
пружины
Собственная
частота колебаний пружины
Проверка
нагрузки пружины
8≤ us
A
Обзор
используемых переменных:
|
d |
диаметр |
|
k |
жесткость |
|
D |
средний |
|
D1 |
наружный |
|
D2 |
внутренний |
|
F |
обобщенное |
|
G |
модуль |
|
H |
рабочая |
|
c |
индекс |
|
Kw |
поправочный |
|
l |
длина |
|
L |
обобщенная |
|
LZ |
длина |
|
m |
масса |
|
n |
количество |
|
o |
высота |
|
t |
шаг |
|
s |
обобщенная |
|
us |
коэффициент |
|
|
плотность |
|
|
напряжение |
|
A |
допустимое |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10. Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.
Пружина сжатия
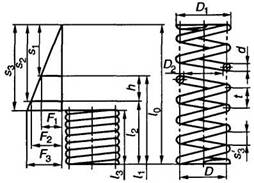
Пружина растяжения
|
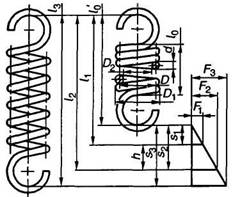
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
1. Сила пружины при предварительной деформации, Н |
F1 |
Принимаются в зависимости от нагрузки пружины |
|
2. Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н |
F2 |
|
|
3. Рабочий ход пружины, мм |
h |
|
|
4. Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с |
Vmax |
|
|
5. Выносливость пружины, число циклов до разрушения |
NF |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
|
6. Наружный диаметр пружины, мм |
D1 |
Предварительно назначают с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
7. Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации |
δ |
δ = 1-F2/F3. (1) Для пружин сжатия классов I и IIδ=0,05…0,25; для пружин растяжения δ=0,05…0,10; для одножильных пружин класса IIIδ=0,10…0,40; для трехжильных класса IIIδ=0,15…0,40 |
|
8. Сила пружины при максимальной деформации, Н |
F3 |
F3=F2/(1-δ) (2) Уточняется по таблицам ГОСТ 13766-86-ГОСТ 13776-86 |
|
9. Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н |
F0 |
F0= (0,1… 0,25) F3 |
|
10. Диаметр проволоки, мм |
d |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86 |
|
11. Диаметр трехжильного троса, мм |
d1 |
|
|
12. Жесткость одного витка пружины, Н/мм |
c1 |
|
|
13. Максимальная деформация одного витка пружины, мм |
s’3 (при F0=0) s”3 (при F0>0) |
Выбирается по таблицам ГОСТ 13764-86-ГОСТ 13776-86
|
|
14. Максимальное касательное напряжение пружины, Н/мм2 (Коэффициент k см. п. 35) |
τ3 |
Назначается по табл. 2 ГОСТ 13764-86. При проверке
Для трехжильных пружин
|
|
15. Критическая скорость пружины сжатия, м/с (Максимальная скорость подвижного звена механизма vmax должна быть равна или меньше vK, т.е. vK > vmax) |
vк |
Для трехжильных пружин
|
|
16. Модуль сдвига, Н/мм2 |
G |
Для пружинной стали G = 7,85·104 |
|
17. Динамическая (гравитационная) плотность материала, Н·с2/м4 |
Р |
p = γ/g, где g-ускорение свободного падения, м/с2; γ – удельный вес, Н/м3. Для пружиннойстали р = 8·103 |
|
18. Жесткость пружины, Н/мм |
с |
Для пружин с предварительным напряжением
Для трехжильных пружин
|
|
19. Число рабочих витков пружины |
n |
n = c1/c (7) |
|
20. Полное число витков пружины |
n1 |
n1 = n+ n2, (8) где n2 – число опорных витков |
|
21. Средний диаметр пружины, мм |
D |
D = D1 – d = D2 + d Для трехжильных пружин D = D1– d1= D2+ d1(9a) |
|
22. Индекс пружины |
i |
i = D/d (10) Для трехжильных пружин i= D/d1 (10а) Рекомендуется назначать от 4 до 12 |
Продолжение табл. 10
|
Наименование параметра |
Обозначение |
Расчетные формулы и значения |
||||
|
23. Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки |
Δ |
Для трехжильного троса с углом свивкиβ=24° определяется по таблице, приведенной ниже |
||||
|
i |
40 |
45 |
50 |
55 |
60 |
7,0 и более |
|
Δ |
1,029 |
1,021 |
1,015 |
1,010 |
1,005 |
1,000 |
|
24. Предварительная деформация пружины, мм |
s1 |
s1=F1/c (11) |
||||
|
25. Рабочая деформация пружины, мм |
s2 |
s2= F2/c (12) |
||||
|
26. Максимальная деформация пружины, мм |
s3 |
s3= F3/c (13) |
||||
|
27. Длина пружины при максимальной деформации, мм |
l3 |
l3 = (n1 + 1 – n3)d, (14) где n3 – число обработанных витков. Для трехжильных пружин l3 = (n + l)d1Δ. (14а) Для пружин растяжения с зацепами l3 = l0 + s3 |
||||
|
28. Длина пружины в свободном состоянии, мм |
l0 |
l0=l3+s3 (15) |
||||
|
29. Длина пружины растяжения без зацепов в свободном состоянии, мм |
l0‘ |
l0‘ = (n1+1)d (15а) |
||||
|
30. Длина пружины при предварительной деформации, мм |
1l |
l1 = l0-s1. (16) Для пружин растяжения l1= l0+s1(16а) |
||||
|
31. Длина пружины при рабочей деформации, мм |
l2 |
l2=l0-s2. (17) Для пружин растяжения l2=l0+s2 (17а) |
||||
|
32. Шаг пружины в свободном состоянии, мм |
t |
t = s’3+d. (18) Для трехжильных пружин t = s’3+d1Δ. (18а) Для пружин растяжения t = d(18б) |
||||
|
33. Напряжение в пружине при предварительной деформации, Н/мм2 |
τ1 |
|
||||
|
34. Напряжение в пружине при рабочей деформации, Н/мм2 |
τ2 |
|
||||
|
35. Коэффициент, учитывающий кривизну витка пружины |
k |
Для трехжильных пружин
|
||||
|
36. Длина развернутой пружины (для пружин растяжения без зацепов), мм |
l |
|
||||
|
37. Масса пружины (для пружин растяжения без зацепов), кг |
m |
|
||||
|
38. Объем, занимаемый пружиной (без учета зацепов пружины), мм3 |
V |
|
||||
|
39. Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм |
λ |
Устанавливается в зависимости от формы опорного витка |
||||
|
40. Внутренний диаметр пружины, мм |
D2 |
D2=D1-2d (25) |
||||
|
41. Временное сопротивление проволоки при растяжении, Н/мм2 |
Rm |
Устанавливается при испытаниях проволоки или по ГОСТ 9389-75 и ГОСТ 1071-81 |
||||
|
42. Максимальная энергия, накапливаемая пружиной, или работа деформации, МДж |
|
Для пружин сжатия и растяжения без предварительного напряжения
для пружин растяжения с предварительным напряжением
|
Методика определения размеров пружин по ГОСТ 13765-86.
1. Исходными величинами для определения размеров пружин являются силы F1 и F2, рабочий ход h, наибольшая скорость перемещения подвижного конца пружины при нагружении или при разгрузке vmах, выносливость NF и наружный диаметр пружины D1 (предварительный).
Если задана только одна сила F2, то вместо рабочего хода h для подсчета берут величину рабочей деформации s2, соответствующую заданной силе.
2. По величине заданной выносливости NF предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.
3. По заданной силе F2 и крайним значениям инерционного зазора δ вычисляют по формуле (2) значение силы F3.
4. По значению F3, пользуясь табл. 2, предварительно определяют разряд пружины.
5. По табл. 11-17 находят строку, в которой наружный диаметр витка пружины наиболее близок к предварительно заданному значению D1. В этой же строке находят соответствующие значения силы F3 и диаметра проволоки d.
6. Для пружин из закаливаемых марок сталей максимальное касательное напряжение τ3 находят по табл. 2, для пружин из холоднотянутой и термообработанной τ3 вычисляют с
учетом значений временного сопротивления Rm. Для холоднотянутой проволоки Rm определяют из ГОСТ 9389-75, для термообработанной – из ГОСТ 1071-81.
7. По полученным значениям F3 и τ3, aтакже по заданному значению F2 по формулам (5) и (5а) вычисляют критическую скорость vK и отношение vmax/vK, подтверждающее или
отрицающее принадлежность пружины к предварительно установленному классу.
При несоблюдении условий vmax/vK<1 пружины I и II классов относят к последующему классу или повторяют расчеты, изменив исходные условия. Если невозможно изменение исходных условий, работоспособность обеспечивается комплектом запасных пружин.
8. По окончательно установленному классу и разряду в соответствующей таблице на параметры витков пружин, помимо ранее найденных величин F3, D1, и d, находят величины c1 и s3, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).
Диаметр проволоки внутренней пружины при заданном диаметре проволоки внешней пружины и индексе пружины Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Пружинный индекс цилиндрической пружины: 5 –> Конверсия не требуется
Диаметр проволоки внешней пружины: 6.5 Миллиметр –> 0.0065 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.0108333333333333 метр –>10.8333333333333 Миллиметр (Проверьте преобразование здесь)
8 Спиральная пружина Калькуляторы
Диаметр проволоки внутренней пружины при заданном диаметре проволоки внешней пружины и индексе пружины формула
Диаметр проволоки внутренней пружины = (Пружинный индекс цилиндрической пружины/(Пружинный индекс цилиндрической пружины-2))*Диаметр проволоки внешней пружины
d2 = (C/(C-2))*d1
РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
При центральном приложении силы в любом поперечном сечении витка пружины возникают результирующая внутренняя сича Р, параллельная оси пружины, к момент 
— плоскость которого совпадает с плоскостью пары сил Р (рис. 6). Нормальное поперечное сечение витка наклонено к плоскости момента под углом а. В этом сечении будут действовать силы и моменты (см. рис. 6)
Ввиду малссти угла подъема витков (обычно 
) можно считать, что сечение пружины работает на кручении.
Максимальное касательное напряжение в сечении пружины
где 
момент сопротивления сечения вала кручению 
учетом кривизны витков и равенства (1) соотношение (2) примет вид
где 
— коэффициент, учитывающий кривизну витков и форму сечеиия (поправка к формуле для кручения прямого бруса); Р — внешняя нагрузка (растягивающая или сжимающая);
Рис. 5. Диаграмма сдвига
Рис. 6. Силовые факторы в сечении нагруженной пружины
— средний диаметр пружины; 
— допускаемое касательное напряжение при кручении (табл. 2).
Значение коэффициента 
для пружин из круглой проволоки при индексе с 
можно вычислить по формуле
а для пружин прямоугольного сечення 
рис. 7.
Для пружин прямоугольного поперечного сечения
2. Допускаемые напряжения для цилиндрических витых пружии растяжения-сжатия
(см. скан)
Рис. 7. (см. скан) К определению коэффициента к для пружин растяжения-сжатия 
тугольного сечения
где 
— высота, 
ширина прямоугольника; а — коэффициент, зависящий от отношения сторои 
(табл. 3).
Если пружина иавита из круглой проволоки, то 
совпадает с полярным моментом сопротивления и тогда
Осевое перемещение торцов пружины с углом подъема 
Податливость пружины наиболее просто определить из энергетических соотношений.
Потенциальная энергия пружины
где 
– крутящий момент в сечении пружины от силы 
; 
— жесткость сечения витка на кручение; 
— полная длина рабочей части витков; 
— число
3. Значения коэффициентов 
(см. скан)
Рис. 8. Характеристика пружииы сжатия
витков пружины; 
— геометрическая жесткость на кручение.
Из соотношения (8) следует:
где 
— осевая податливость одного витка (осадка в мм при действии 
),
Для пружины из круглой проволоки полярный момент инерции сечения
и тогда формула 
примет вид
где 
— модуль сдвига, 
модуль упругости материала пружины. Для пружин с прямоугольным поперечным сечеиием
где а — наименьшая сторона сечеиия (коэффициент 
по табл. 3).
Геометрическая жесткость на кручение для прямоугольного сечения
коэффициент 
— по табл. 3.
На рис. 8 показана зависимость между нагрузкой и осадкой пружины сжатия. Если пружина установлена с предварительной затяжкой (осадкой) с усилием 
то ее установочная длина
Длииа пружины при действии наибольшей внешней нагрузки 
При действии нагрузки 
соответствующей 
длина пружины будет наименьшей:
В соотношениях 
— длииа пружины в свободном (ненагруженном) состоянии.
Угол наклона прямой 
(см. рис. 8) к оси абсцисс
В зависимости от назначения пружины усилие предварительной затяжки 
Наибольшая допускаемая внешняя нагрузка для пружии растяжения и сжатия
Конечный участок диаграммы пружины от силы 
до усилия 
сжимающего пружину до соприкосновения витков, может оказаться нелинейным из-за неравномерности шага.
Рабочий ход (осадка) пружины
Если ход пружины задан, то необходимое число рабочих витков для обеспечения этого перемещения
Число витков округляют до полувитка 
и до одного витка при 
Полное число витков
Дополнительные 
витка идут на поджатие для создания опорных поверхностей у пружины.
Полная длина ненагруженной пружины
где 
-длина пружины, сжатой до соприкосновения соседних рабочих витков 
— шаг пружины, находящийся в зависимости от наибольшей осадки пружины,
где наибольшая осадка пружины
В табл. 4 приведены значения наибольших допускаемых внешних нагрузок 
и податливостей витка пружины X в зависимости от индекса с и диаметр а проволоки 
Длина проволоки, необходимая для изготовления пружины,
где а — угол подъема витков ненагруженной пружины, 
6-7-9°.
Для предотвращения выпучивания пружины от потери устойчивости ее гибкость 
должна быть менее 2,5.
Если по конструктивным соображениям это ограничение не выполняется, то пружину, как указано выше, следует ставить на оправках или монтировать в Гильзах.
Длина пружины растяжения в ненагруженном состоянии
где 
— высота одного зацепа, 
Длина пружины при максимальной внешней нагрузке 
где ?! — усилие первоначального сжатия витков при навивке.
Для изготовления пружины из проволоки
здесь 13 — длина проволоки для одного зацепа.
Расчет пружин обычно начинают с определения диаметра проволоки (или размера сечения для некруглой проволоки), задаваясь значением 
и индексом пружины с.
Диаметр проволоки находят из условия прочности (7)
Если пружина имеет прямоугольное сечение, то ширина прямоугольника
Далее по формулам (13), (21)-(27) определяют размеры пружины.
Расчет цилиндрических пружин растяжения — сжатия из проволоки круглого сечения при 
мм; с 
можно проводить, используя табл. 4.
Пример 1. Заданы: ход пружины 
усилие предварительной затяжки 
и наибольшая внешняя нагрузка 
Из соотношения (19) находим 
и далее по табл. 4 подбираем 
и X. Потребное число витков пружины находим из соотношения (21), а размеры пружины — по формулам 
Пример 2. Заданы: наибольшая нагрузка 
установочная длина 
и ход пружины 
По табл. 4 для заданного значения 
после вычисления 
находим 
и X. Потребное число витков пружины и ее размеры находим, задаваясь значением 
или 
(кликните для просмотра скана)
(кликните для просмотра скана)
Рис. 9. Фасонные пружины
Решение задачи такого типа не однозначно, на выбор того или иного варианта могут влиять дополнительные конструктивные соображения, связанные, например, с выбором Р. и 
Выбор пружин из проволоки диаметром от 0,2 до 50 мм для сталей, приведенных в табл 2 проводят по ГОСТ 13764-86 – ГОСТ 13776-86. Эти стандарты распространяются на вянтовые цилиндрические пружины растяжения и сжатия для нагрузок от 1 до 
с индексами 
и наружными диаметрами 1—700 мм. В зависимости от долговечности стандартные пружинь! делятся на классы (см. табл. 2).
При больших нагрузках и ограниченных габаритах используют составные пружины сжатия (см. рис. 3) — набор из нескольких (чаще двух) концентрически расположенных пружин, одновременно воспринимающих внешнюю нагрузку. Для предотвращения сильного закручиваиня торцовых опор и перекосов навивку соседних пружин выполняют в противоположных направлениях (левом и правом). Опоры выполняют так, чтобы обеспечивалась взаимная центровка пружин (см. рис. 3, 4).
Обычно составные пружины имеют одинаковые осадки. При их проектировании стремятся к тому, чтобы длины пружин, сжатых 
соприкосновения витков, были приблизительно одинаковы, а наибольшие касательные напряжения у всех пружин были равны допускаемому.
Первые Два условия для пружин, навитых из круглой проволоки, эквивалентны равенству их индексов.
При расчете двух концентрических клапанных пружин автотракторных двигателей часто средние диаметры пружин выбирают по конструктивным соображениям (в зависимости от диаметра горловины клапана) Радиальный зазор в таких пружинах составляет 2 мм.
Далее, принимая, что наружная пружина воспринимает 50—70% внешней нагрузки, находят диаметр проволоки (
— номер пружины)
и определяют длину пружины.
В последние годы получили распространение многожильные пружины, при изготовлении которых вместо одной проволоки используется трос, свитый издвх — шести проволок малого диаметра 
. По конструктивному решению такие пружины эквивалентны концентрическим пружинам. Благодаря высокой демпфирующей способности (за счет трения между жилами) и податливости многожильные пружины хорошо работают в амортизаторах и других подобных устройствах. При действии переменных нагрузок многожильные пружины довольно быстро выходят из строя от изнашивания жил.
В конструкциях, работающих в условиях вибраций нагрузок, иногда применяют фасонные пружины (рис. 9) с нелинейной зависимостью между внешней силой и упругим перемещением пружины
Расчет фасонных и многожильных пружин дан в работе 16], гл. 27.
