Как найти диаметр сечения шара плоскостью

  На данном Вами рисунке треугольник АОО1 – равнобедренный прямоугольный. Углы при диаметре сечения в рисунке равны. Обойдемся без него. 

——————————————————————————
Смотрим на схематический  рисунок, данный во вложении к задаче. 
АС– диаметр шара и равен двум его радиусам.  

АВ– диаметр сечения, также равен двум радиусам сечения.
Диаметр шара можно определить из прямоугольного треугольника АВС, где угол В – прямой, т.к угол АВС опирается на диаметр АС,

АС – гипотенуза, и

Напомним,
что шаром называется тело, состоящее из всех точек пространства,
находящихся на расстоянии не большем заданного от некоторой данной точки. Эта
точка – центр шара, а заданное расстояние – радиус шара.

Шар
так же, как цилиндр и конус, является телом вращения. Он получается в
результате вращения полукруга вокруг его диаметра.

Поверхность,
образуемая при этом вращении полуокружности, называется сферой. Можно
сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность
есть граница круга, так и сфера – это граница шара.

Назовём
элементы сферы и шара.

Радиус
сферы – это отрезок, соединяющий центр сферы и любую её точку.

Хорда
сферы – отрезок, соединяющий две точки сферы.

Диаметр
сферы – хорда сферы, проходящая через её центр.

Радиус,
хорда, диаметр шара – это радиус, хорда, диаметр его сферы.

Любое
сечение шара плоскостью есть круг. Центром этого круга является основание
перпендикуляра, опущенного из центра шара на секущую плоскость.

Плоскость,
которая проходит через центр шара, называется диаметральной плоскостью.
Сечение ею шара – большим кругом, а сечение сферы – большой
окружностью.

Любая
диаметральная плоскость шара является его плоскостью симметрии. Центр
шара является его центром симметрии.

Плоскость,
проходящая через точку А сферы и перпендикулярно радиусу, проведённому в
эту точку, называется касательной плоскостью. Точка А называется точкой
касания.

Свойство
касательной плоскости к сфере: радиус сферы,
проведённый в точку касания, перпендикулярен касательной плоскости.

Признак
касательной плоскости к сфере: плоскость,
перпендикулярная радиусу сферы в конечной его точке на сфере, является
касательной к сфере.

Касательная
плоскость пересекается с шаром в единственной точке – в точке касания.

Касательной
прямой к сфере (шару) называется прямая, имеющая со сферой
единственную общую точку.

Отрезки
касательных к сфере, проведённые из одной точки, равны и составляют равные углы
с прямой, проходящей через эту точку и центр сферы.

Линией
пересечения двух сфер является окружность.

Площадь
сферы радиуса : .

Объём
шара
радиуса : .

Шаровым
сегментом называется часть шара, отсекаемая от него плоскостью.
Площадь боковой поверхности шарового сегмента:

 .

Объём
шарового сегмента:

,

где
 –
радиус шара,  –
высота шарового сегмента.

Шаровым
сектором называется тело, которое получается из шарового
сегмента и конуса, основанием которого является сечение плоскостью данного шара.

Площадь
боковой поверхности шарового сектора:

 .

Объём
шарового сектора:

,

где
 –
радиус шара,  –
высота сегмента.

Шар
называется вписанным в многогранник, а многогранник – описанным около
шара, если поверхность шара касается всех граней многогранника.

Шар
называется описанным около многогранника, а многогранник – вписанным
в шар, если поверхность шара проходит через все вершины многогранника.

Шар
называется вписанным в цилиндр, а цилиндр – описанным около шара,
если поверхность шара касается оснований цилиндра и всех образующих.

Шар
называется описанным около цилиндра, если окружности оснований цилиндра
принадлежат поверхности шара.

Шар
называется вписанным в конус (усечённый конус), а конус
(усечённый конус) – описанным около шара, если поверхность шара касается
основания (оснований) конуса и всех образующих.

Шар
называется описанным около конуса (усечённого конуса), если окружность
основания и вершина (окружности оснований) конуса принадлежат поверхности шара.

Если
боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую
пирамиду можно вписать шар.

Около
пирамиды можно описать шар тогда и только тогда, когда около её основания можно
описать окружность.

Если
боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости
основания), то около такой пирамиды можно описать шар.

В
призму можно вписать шар тогда и только тогда, когда в перпендикулярное
сечение этой призмы можно вписать окружность, а высота призмы равна диаметру
окружности, вписанной в это перпендикулярное сечение.

Описать
шар около призмы можно тогда и только тогда, когда призма прямая и около её основания
можно описать окружность.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. Радиус шара увеличили в  раза.
Во сколько раз увеличился объём шара?

Решение.

Задача
вторая. Объём шара равен  см³.
Найдите диаметр шара.

Решение.

Задача
третья. Шар пересечен плоскостью. Площадь сечения равна  см².
Расстояние от центра шара до плоскости сечения равно  см.
Найдите площадь поверхности шара.

Решение.

Задача
четвёртая. В конус с радиусом основания, равным  см,
и высотой, равной  см,
вписан шар. Найдите отношение площади боковой поверхности конуса к площади
поверхности шара.

Решение.

Задача
пятая. Найдите объём шарового сектора, если радиус
окружности его основания равен  см,
а радиус шара –  см.

Решение.

Задача
шестая. Шар с радиусом  см
пересечён плоскостью, находящейся на расстоянии  см
от центра шара. Найдите площадь сечения.

Решение.

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг  его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

S = 4 πr²

S = πd²,

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr³,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

 

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

S = 2πRh,

где R – радиус большого круга, h – высота шарового сегмента.

Объём шарового сегмента можно найти по формуле:

V = πh²(R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

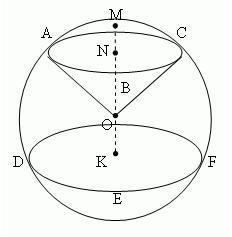
Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR²H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги  ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Содержание

• – Что представляет собой Диаметральное Сечение шара?
• – Что является осевым сечением сферы?
• – Как найти плоскость сечения шара?
• – Что такое Диаметральное сечение?
• – Что такое сечение шара?
• – Что представляет собой сечение шара плоскостью что такое большой круг шара?
• – Какой фигурой является осевое сечение?
• – Как называется Цилиндр осевое сечение которого квадрат?
• – Что представляет собой осевое сечение цилиндра?
• – Как рассчитать сечение цилиндра?
• – Как вычислить площадь сечения?
• – Как найти осевое сечение конуса?
• – Что такое диаметр круга?
• – Сколько общих точек с шаром имеет касательная плоскость?
• – Что такое сфера и чем отличается от шара?

Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара). При решении заданий удобнее вместо шара чертить один из больших кругов, а плоскость сечения заменить хордой этого круга.

Что представляет собой Диаметральное Сечение шара?

Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью Любая диаметральная плоскость шара являются его плоскостью симметрии.

Что является осевым сечением сферы?

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ( R ) от данной точки (центра сферы О ). Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Как найти плоскость сечения шара?

S = π * d 2 / 4, где

d – диаметр окружности шара в этой плоскости.

Что такое Диаметральное сечение?

Секущая плоскость – это плоскость, которая пересекает сферу. Определение. Диаметральная плоскость – это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг.

Что такое сечение шара?

Плоскость, проходящая через центр сферы (шара) называется диаметральной плоскостью. Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).

Что представляет собой сечение шара плоскостью что такое большой круг шара?

Сечение шара, проходящее через центр, называется большим кругом, не проходящее — малым кругом. Центр большого круга совпадает с центром шара, а центр малого круга является основанием перпендикуляра, опущенного из центра шара на плоскость этого круга.

Какой фигурой является осевое сечение?

Объяснение: Осевое сечение цилиндра – прямоугольник. Оно выполняется плоскостью, которая проходит по оси цилиндра.

Как называется Цилиндр осевое сечение которого квадрат?

Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149). Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис.

Что представляет собой осевое сечение цилиндра?

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью. Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

Как рассчитать сечение цилиндра?

Площадь сечения цилиндра

1. S = π * d 2 / 4, где d – диаметр цилиндра. Формула для расчета площади осевого сечения цилиндра:
2. S = d * h, где d – диаметр цилиндра; h – высота цилиндра. …
3. S = a * h, где a – хорда основания цилиндра; h – высота цилиндра.

Как вычислить площадь сечения?

Площадь сечения круга или шара можно найти по формуле:

1. S = πR2 …
2. c = S*q*r*t*(a2 + b2) …
3. S= c*h. …
4. S=a*b. …
5. S =2R*h. …
6. S =2а*h.

Как найти осевое сечение конуса?

Формула для расчета площади основания конуса:

1. S = π * d 2 / 4, где d – диаметр конуса. Формула для расчета площади осевого сечения конуса:
2. S = d * h / 2, где d – диаметр конуса; h – высота конуса. …
3. S = a * h / 2, где a – хорда основания конуса; h – высота конуса.

Что такое диаметр круга?

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). … Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Сколько общих точек с шаром имеет касательная плоскость?

1) Касательная прямая и сфера имеют только одну общую точку; 2) касательная прямая перпендикулярна к радиусу сферы, проведенному в точку касания. Касательные к сфере, проведенные из внешней точки, равны.

Что такое сфера и чем отличается от шара?

Сфера имеет свою площадь, но при этом у нее нет объема. … Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри. Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра.

Интересные материалы:

Что значит друзья не разлей вода?
Что значит духи селектив?
Что значит думать абстрактно?
Что значит два пальца на вене?
Что значит две октавы?
Что значит две Скобочки в переписке?
Что значит две трети от числа?
Что значит двери под ключ?
Что значит двойное полнолуние?
Что значит двойной интервал в ворде?