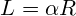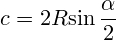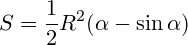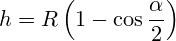Как найти диаметр сегмента

Как найти диаметр сегмента

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

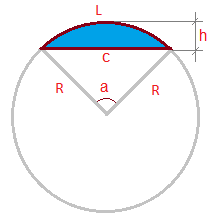
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Как найти диаметр окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

  • Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
  • Отметить точки пересечения прямой и окружности.
  • Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
  • Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
  • Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

Всё про окружность и круг

Окружность – это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол – это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/diametr-okruzhnosti

http://www.stranamam.ru/post/8974384/

[/spoiler]

Источник

HOUSEHAND.ru —

Сегмент — плоская фигура, заключённая между дугой и её хордой. Как частный случай, круговой сегмент: часть круга, ограниченная дугой окружности и её хордой или секущей.

Для начала расчёта выберите известные параметры, по которым будут произведены расчёты, за тем введите их и нажмите кнопку «Рассчитать».

Если Вам необходим узнать по каким формулам ведется расчет для фигуры, а так же задать единицы измерения или сохранить расчет в PDF, то воспользуйтесь сайтом calc-online24.ru

Вычисление диаметра трубы по хорде

Бывают ситуации, когда необходимо измерить диаметр чего-либо, например, трубопровода, но нет возможности измерить длину окружности (из-за изоляции или температуры).

В этом случае можно применить метод вычисления диаметра по хорде. Для этого метода необходим только штангенциркуль.

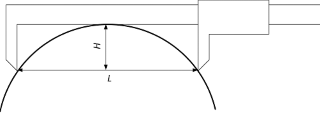
  1. Прикладываем его, как показано на рис. 1;
  2. измеряем длину L;
  3. измеряем высоту губок штангенциркуля Н;
  4. вычисляем диаметр по формуле D = (L 2 ⁄ 4H) + H или
  5. вычисляем радиус по формуле r = (L 2 + 4H 2 ) ⁄ 8H

Вычисление диаметра трубы по хорде с использованием штангенциркуля

Рисунок 1

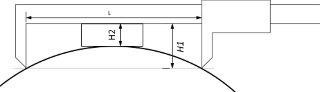
Если под рукой только «штангель» с длинными губками или не хватает его измеряемого диапазона можно применить какую-нибудь «проставку». В идеале подойдёт плоскопараллельная концевая мера… 😉 Её надо вставить, как показано на рисунке 2, и при вычислении, от длины губок отнять высоту этой «проставки». Н = Н1 — Н2

Вычисление диаметра трубы по хорде с использованием штангенциркуля и проставки

Рисунок 2

Точность этого метода зависит, только от инструмента, который Вы будете применять.

Длина хорды и высота сегмента круга

Сегмента круга - радиус, площадь, хорда, дуга, периметр, высота, угол

Зная длину хорды и высоту сегмента круга, необходимо для вычисления всех остальных параметров воспользоваться одновременно обеими формулами, выразив через них радиус круга. c=2r sin⁡〖α/2〗 h=r(1-cos⁡〖α/2〗 ) r=h/2+c^2/8h

Угол сегмента круга можно выразить через любую из вышеприведенных формул для хорды и высоты сегмента. В случае с хордой синус половинного угла будет равен ее длине, деленной на два радиуса. sin⁡〖α/2〗=c/2r

Длина дуги и площадь сегмента круга вычисляются по стандартным формулам, в которые необходимо подставить полученное для радиуса выражение. P=αr=α(h/2+c^2/8h) S=r^2 (α/2-sin⁡α )=1/2 (h/2+c^2/8h)^2 (α-sin⁡α )

Источник

При заполнении данных, обратите внимание на дополнительную информацию со знаком Расчет параметров сегмента круга

——————————– Было полезно? Поддержите проект?! Мы хотим чтобы наш сайт был бесплатным. Не хотим подключать личный кабинет и брать за это плату. Но для поддержания и развития необходимы средства. Будем признательны за любой денежный вклад👇 от 5 рублей до 1.000.000 $ 😉 ———————————- ———————————

Если Вам понравился данный материал, пожалуйста, посоветуйте его своим друзьям в социальных сетях с помощью кнопок расположенных ниже.

При копировании материала на другие сайты ссылка на наш сайт как источник обязательна, потому, как даже в сети можно и нужно оставаться вежливыми людьми.

Мы рады видеть Вас на нашем сайте!

08 декабря 2022   —   Admin

Источник

  • Создать сайт

  • Домены

  • VPS сервер

  • VDS сервер

  • Хостинг

  • Саппорт

  • Контакты

  • Главная

  • Онлайн калькуляторы

  • Математика


  • Сегмент круга

Сегмент круга

Данный калькулятор считает параметры сегмента круга, а именно:

  • длину дуги (L),
  • длину хорды (C),
  • площадь (S),
  • высоту (h),

Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:

1) сегмент круга решается с помощью радиуса (R) и угла (A).

2) сегмент круга находим с помощью высоты и длины хорды.

Однако, как справедливо заметил наш пользователь:“на практике hourто случается, что как радиус дуги, так и угол неизвестны” (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Параметры сегмента по хорде и высоте

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
R=frac{h}{2}+frac{c^2}{8h}

Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:
alpha=2arcsin{ frac{c}{2R} }
Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Источник
Сегмент круга
Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
S=frac{1}{2}R^2(alpha-sin{alpha}) [1]
Длина дуги:
L={alpha}R
Длина хорды:
c=2{R}{sin{frac{alpha}{2}}}
Высота сегмента:
h={R}left(1-{cos{frac{alpha}{2}}}right)

PLANETCALC, Сегмент

Сегмент

Угол в градусах, образуемый радиусами сектора

Точность вычисления

Знаков после запятой: 2

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

PLANETCALC, Параметры сегмента по хорде и высоте

Параметры сегмента по хорде и высоте

Точность вычисления

Знаков после запятой: 2

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
R=frac{h}{2}+frac{c^2}{8h}

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
alpha=2arcsin{ frac{c}{2R} }
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

PLANETCALC, Площадь сегмента круга по радиусу и высоте

Площадь сегмента круга по радиусу и высоте

Точность вычисления

Знаков после запятой: 2

Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
alpha=2arccosleft(1-frac{h}{R}right)
далее используется формула [1] для получения площади.

15 вычислений по сегменту круга в одной программе

Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:

  • длина дуги
  • угол
  • хорда
  • высота
  • радиус
  • площадь

Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.

PLANETCALC, Круговой сегмент - все варианты расчета

Круговой сегмент – все варианты расчета

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Источник

Добавить комментарий