Как найти диаметр шара по экватору

Как найти диаметр Земли

Давно отошли в прошлое те времена, когда Земля считалась плоскостью. Сегодня даже детям известно, что планета представляет собой шар. Но если Земля шарообразная, значит, можно определить ее диаметр.

Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.

Применительно к Земле такое не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».

Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.

Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.

Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.

Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.

Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).

В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.

Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.

На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по меридиану – 40 007,86. Эратосфен лишь немного ошибся.

Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.

Источники:

• Как измерили Землю

Диаметр Земли имеет для ученых важное значение. С его помощью можно вычислить площадь нашей планеты и расстояние до ее центра, также он помогает составлять карты и проводить запуски космических летательных аппаратов. Узнаем, как вычисляются эти параметры и каковы их значения.

Основные параметры Земли

1. Диаметр по экватору – 12756 км, по полюсам – 12713 км.
2. Средний радиус – 6371 км. На таком расстоянии от поверхности находится центр ядра. Экваториальный радиус Земли – 6378 км. Расстояние к центру Земли на полюсах – 6356,5 км.
3. Окружность Земли по экватору – 40075 км, а по полюсам – 40008 км.
4. Удаление от Солнца в километрах – приблизительно 150 миллионов. Оно наиболее подходяще для формирования и поддержания жизни. Если бы орбита Земли была ближе или дальше всего на несколько миллионов километров, условия для эволюции жизни были бы намного хуже.
5. Время, за которое Земля совершает один оборот вокруг Солнца – 365 дней 5 часов 48 минут и 46 секунд. В течение 23 часов 46 минут и 4 секунды она совершает оборот вокруг своей оси. Каждые 100 лет эта скорость уменьшается на 0,017 секунд. 140 млн. лет потребуется для того, чтобы длительность суток увеличилась на час.
6. Ось вращения планеты наклонена к плоскости орбиты под углом немногим больше 23 градусов. Это обусловливает сезонность климатических условий и четкую смену времен года. Если бы ось вращения была наклонена на несколько градусов меньше или больше – на Земле создались бы менее благоприятные климатические условия, на больше части поверхности образовались бы ледники.
7. Средняя температура на Земле – примерно 15 °C.
8. Вода занимает примерно 71% всей площади. Ее масса – 1460 миллионов миллиардов тонн. Атмосфера весит в 275 раз меньше. Ее масса – немногим больше 5 квадриллионов тонн.
9. В атмосфере 21 % кислорода. Основную массу занимает азот – биологически инертный газ, его в составе атмосферы 78%.
10. Масса Земли – примерно 6*10²⁴ килограмма.
11. Объем планеты – 1,08*10¹² км³.
12. Площадь земного шара – 510 млн км².
13. Плотность – 5,5 г/см³.
14. Наиболее близкое к нам небесное тело – Луна. Ее среднее расстояние от Земли – примерно 384 тыс. км.

Форма планеты

На вопрос, какая форма у Земли, большинство людей ответит, что шарообразная. И здесь они сделают ошибку. На планету влияют силы гравитации: огромная масса тяготеет к ядру, поэтому происходит постоянное сжатие. Наиболее сильная центробежная сила, появляющаяся из-за движения Земли вокруг собственной оси – на экваторе.

Земля является своего рода «неправильным шаром». Сжатие является причиной того, что экваториальный диаметр планеты немногим больше, чем по полюсам. Ученые определяют форму нашей планеты как близкую к «сплюснутому эллипсоиду».

Интересно, что по причине пренебрежения сжатием Земли по полюсам, эталон метра от 1795 года оказался на 200 микрон короче.

В форме планеты важна также местная топография. Конечно же, она не может в глобальном масштабе влиять на форму планеты. Так, различия между горой Эверест и Марианской впадиной составляет примерно 19 км. В глобальных масштабах эта цифра незначительна. Максимальное расстояние от центра Земли до экватора, учитывая выпуклость земной поверхности  – это вершина вулкана Чимборасо, находящегося в Эквадоре.

Что такое экватор и для чего он нужен

Под экватором следует понимать линию, перпендикулярную оси, вдоль поверхности Земли, на одинаковом расстоянии от полюсов.

Вдоль всей этой линии день равняется ночи. Правда, из-за атмосферной рефракции продолжительность дня больше на несколько минут. Два раза в год (в дни равноденствий) Солнце находится в зените, и лучи будут направляться строго перпендикулярно земной поверхности. Широта на экваторе – 0°.

Экватор имеет важнейшее значение для определения широты географического объекта.  Все точки, находящиеся к югу от воображаемой линии, имеют южную широту. А объекты, располагающиеся к северу от нее, соответственно, имеют северную широту.

Как измерить длину окружности земли

Размер Земли поддается вычислению. Для измерения длины окружности Земли пользуются высокотехнологичными приборами и спутниками. Однако до появления этих изобретений приходилось пользоваться математическими методами измерений. В 18 веке ученые П. Мешен, А.М. Лежандр, Ц. Кассини использовали способ триангуляции.

Предположим, что нужно измерить дистанцию между некоторыми точками, удаленными на несколько сотен километров. Для этого нам надо построить на местности опорную сеть. Это можно сделать с помощью треугольников. Их вершинами будут места, находящиеся на высоте. На них сооружаются воображаемые пирамиды так, чтобы они направлялись на близко расположенные пункты.

Воображаемые фигуры должны быть удобными для установки угломера и вычисления градусов углов. В одном из треугольников измеряют одну сторону, пролегающую по ровной местности. Это будет базис.

Простейший способ измерения длины экватора – умножить количество километров в одном градусе на 360.

Измерение окружности начинается с треугольника, являющегося базисом. По стороне и по углам вычисляется другие стороны этой фигуры. Одна из них является также стороной смежного треугольника. Она же является исходной для определения сторон иного треугольника. В ходе математических вычислений можно найти параметры последнего треугольника. Так можно получить значение дуги меридиана. Чем длиннее дуги меридианов, тем лучше можно вычислить нужную величину – радиус нашей планеты.

Когда известна протяженность дуги меридиана, несложно посчитать, какая будет длина одного градуса. Такой метод является основой геодезии.

Как вычислить радиус и диаметр планеты

Радиус и диаметр Земли вычислить несложно. Для этого пользуются формулами d=l/π; r=½*π. Буквы означают:

• d – диаметр;
• l – протяженность окружности;
• r – радиус (линия, проложенная от центра и до любой точки на окружности);
• π – число, приблизительно равное 3,14.

Измерение окружности Земли в древние времена

О длине этой величины было известно еще в Древней Греции. Необходимые расчеты были сделаны древнегреческим математиком, астрономом, географом Эратосфеном. Ему было известно о том, что в день солнцестояния 21 июня в Сиене, находящейся за полтысячи миль от Александрии, в полдень освещалось дно колодцев, а от предметов не обнаруживалась тень. Выходит, Солнце в этом участке планеты было в зените. В Александрии ничего подобного не происходило.

В полдень летнего солнцестояния ученый измерил тень от городского обелиска (ему была известна его высота). Так было установлено, что Александрию и Сиену отделяет 7 градусов широты.

Астроном делал вычисления дальше. 7° – это примерно одна пятидесятая часть окружности, равняющейся 360°. Умножив расстояние от Сиены до Александрии на 50, у математика получилось число 25000. Стольким милям равнялась окружность Земли.

Длина окружности Земли, рассчитанная Эратосфеном, немного меньше фактической. Это объясняется не примитивностью расчетов: этот способ узнать окружность Земли достаточно точный. Во времена жизни Эратосфена никто не знал точной дистанции между этими населенными пунктами. Также ученый не принял во внимание то, что оба города расположены на двух разных меридианах.

В средние века упоминания о подобных исследованиях были запрещены церковью. Только в 16 веке кругосветное путешествие Ф. Магеллана позволило убедиться, что планета действительно имеет округлую форму, и что окружность ее действительно равна 40 тыс. км.

Сколько времени нужно, чтобы обойти вокруг Земли пешком

Зная сколько километров составляет длина окружности Земли по экватору, можно вычислить, сколько времени понадобится, чтобы обойти его пешком. Если взять за основу обычную скорость пешехода 6 километров в час, то, воспользовавшись формулой t=S/V, можно получить значение примерно 6700 часов, или 278 суток.

Столько понадобится для того, чтобы пройти пешком вокруг Земли без передышки. Если же допустить, что воображаемый пешеход будет каждый день проходить по 6 часов, то для совершения такого путешествия ему понадобится около 1110 суток, или более 3 лет.

Интересная информация об экваторе Земли

На экваторе круглогодично жаркий и влажный климат. Леса Амазонки и экваториальной Африки, Индонезии отличаются разнообразием растительного и животного мира. Днем температура колеблется между 25 и 30 градусами. Ночью не намного холоднее: настолько сильно прогревается поверхность земли солнечными лучами.

Однако экватор интересен некоторыми географическими особенностями:

• он проходит сквозь более 30 островов;
• пересекает 14 стран;
• Эквадор имеет такое название в честь экватора;
• в большинстве экваториальных государств установлены памятники и памятные знаки в честь нулевой параллели;
• недалеко города Кито располагается вулкан Каямбе высотой около 4,7 км, с белеющей от вечного льда вершиной (и это несмотря на то, что экваториальный климат отличается постоянной жарой);
• река Конго, которая течет в центре африканского материка, проходит через нулевую параллель дважды;
• поскольку в рассматриваемой области Земля обращается очень быстро, здесь легче всего запускать спутники: они быстрее набирают необходимую скорость.

Размеры Земли – одни из главных параметров в астрономии и имеет большое практическое значение. С ее помощью можно узнать диаметр и радиус Земли. Вычислить эти параметры можно, применяя несложные математические вычисления.

Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.

Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.

Способ вычисления диаметра шара при известном значении объёма фигуры

Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:

D = √(S ⁄ π)

где S — площадь поверхности шара

Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.

Способ нахождения диаметра шара при заданном значении его объёма

Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда

D = ³√(6V / π)

где V — объём шара

Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.

В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.

Окружность шара, сферы

Свойства

Зная окружность шара, можно напрямую найти радиус и диаметр шара, разделив известное значение на удвоенное число π для вычисления радиуса, и просто на число π для вычисления диаметра. r=P/2π d=P/π

Площадь поверхности шара по определению равна четырем произведениям числа π на квадрат радиуса, поэтому подставив вместо последнего отношение длины окружности сферы к двум числам π, формула принимает вид произведения числа π на квадрат длины окружности. S=4πr^2=P^2/π

Объем сферы, зная длину окружности сферы, можно найти, подставив отношение, через которое выражен радиус, в формулу объема. Тогда объем будет равен отношению куба длины окружности к шести квадратам числа π. V=4/3 πr^3=4/3 π(P/2π)^3=P^3/(6π^(2 ) )

Калькулятор круга

Калькулятор круга – это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Диаметр шара. Калькулятор и формулы

С помощью этого простого калькулятора можно без труда найти диаметр шара и остальные величины, такие как радиус, площадь и объем шара. Все, что нужно сделать, это заполнить любой один слот и нажать на кнопку “Рассчитать”. В итоге отобразятся все 4 величины вместе с формулами вычисления.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

[spoiler title=”источники:”]

http://tellaboutall.ru/services/circle/

[/spoiler]

§ Окружность. Длина окружности. Число Пи

Длина окружности. Число Пи
Площадь круга
Площадь сферы. Объём шара

Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.

Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.

Число π и длина окружности

Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.

В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.

Запомните!

Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).

π ≈ 3,14…

Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,

округленное до разряда сотых
π ≈ 3,14…

Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.

Запомните!

Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).
C = πD
C = 2πR
, так как D = 2R

Как найти длину окружности

Чтобы закрепить полученные знания, решим задачу на окружности.

Разбор примера

Условие задачи:

Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.

Воспользуемся формулой длины окружности:

C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см

Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.

Разбор примера

Условие задачи:

Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).

Выразим из формулы длины окружности диаметр.

C = πD
D = С / π

D = 56,52 / 3,14 = 18 дм

Хорда и дуга окружности

На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.

Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.

Важно!

Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».

Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.

Длина окружности.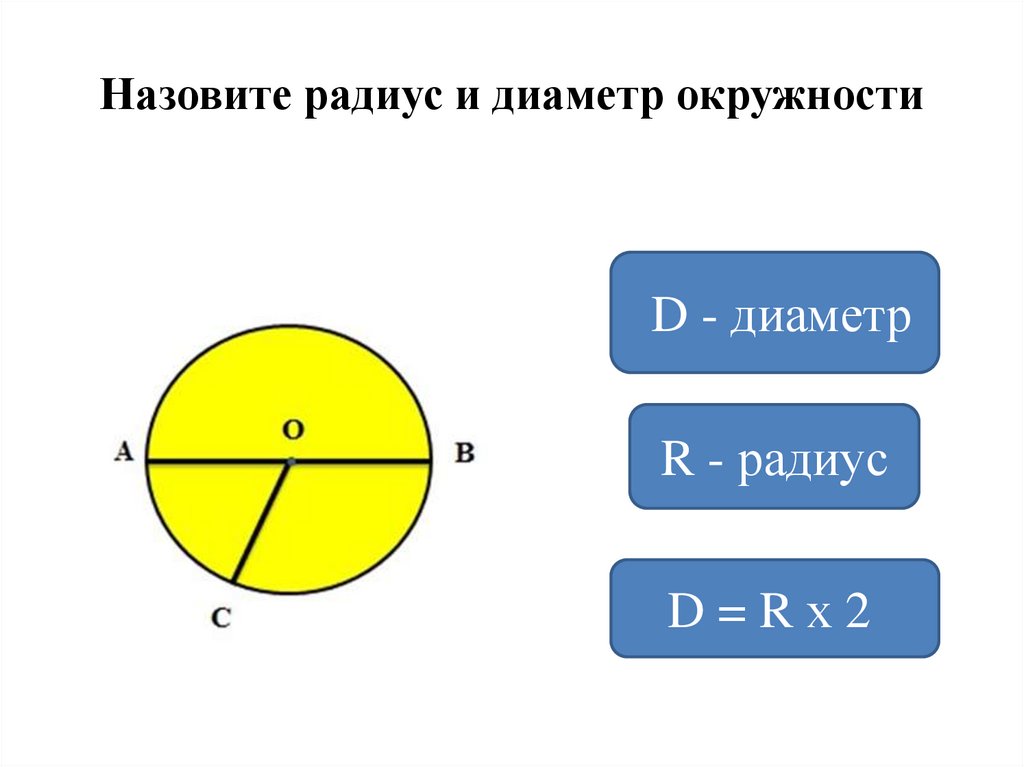 Число Пи
Площадь круга
Площадь сферы. Объём шара

формула и пояснения :: SYL.ru

Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?

Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.

Круг и окружность

Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.

А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.

После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.

Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.

Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.

Формула окружности через диаметр

Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.

Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.

Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.

Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).

Как вычислить диаметр: формула

На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания.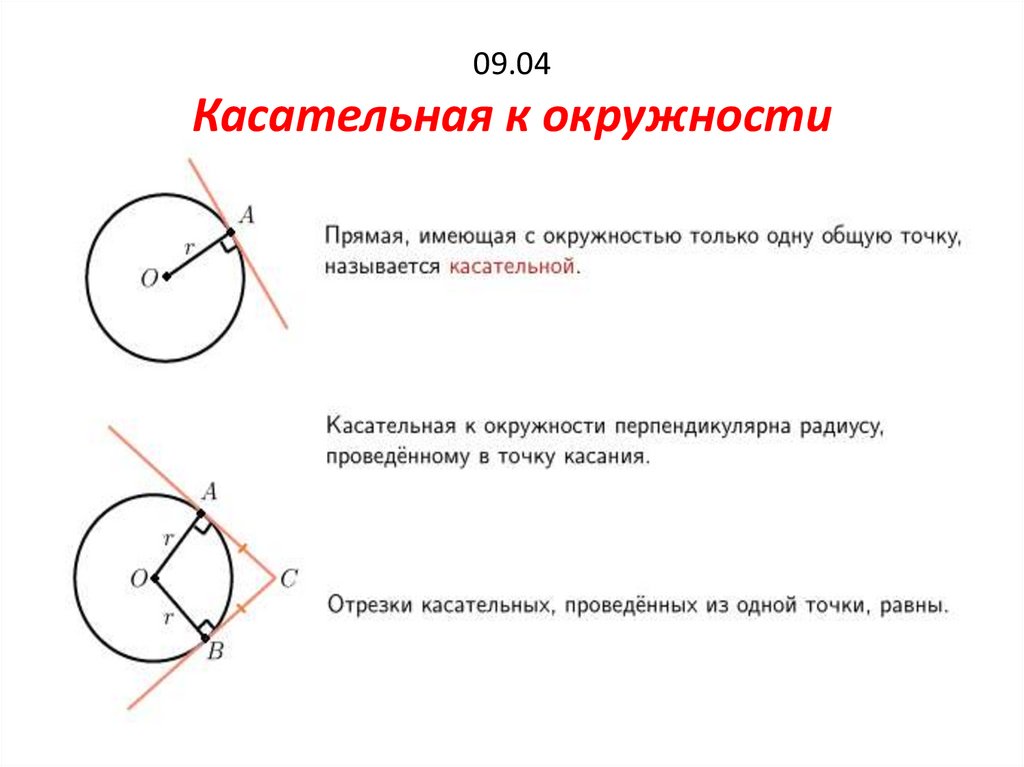 Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.

Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?

Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.

Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.

Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.

Как измерять окружности — манекены

Авторы: Марк Зегарелли и

Обновлено: 09.07.2021

Алгебра для чайников

Исследовать книгу Купить на Amazon

Центр окружности — это точка, которая находится на одинаковом расстоянии от любой точки самой окружности. Это расстояние называется радиусом окружности, или р для краткости. И любой отрезок линии от одной точки окружности через центр к другой точке окружности называется диаметром или сокращенно d .

Диаметр

Как видите, диаметр любого круга состоит из одного радиуса плюс еще один радиус, то есть два радиусов (произносится как луч
-ди-ай). Это понятие дает вам следующую удобную формулу:

Например, учитывая окружность с радиусом 5 миллиметров, вы можете вычислить диаметр следующим образом:

Окружность

Поскольку круг имеет особую форму, его периметр (длина его «сторон») имеет особое название: окружность (сокращенно C ). Ранние математики приложили немало усилий, чтобы выяснить, как измерить длину окружности. Вот формула, которую они нашли:

Примечание: Поскольку 2 x r равно диаметру, вы также можете записать формулу как C = π x д .

Символ π называется пи (произносится как «пирог»). Это просто число, приблизительное значение которого выглядит следующим образом (десятичная часть числа пи продолжается бесконечно, поэтому вы не можете получить точное значение числа пи):

.

Итак, зная окружность радиусом 5 мм, можно вычислить примерную длину окружности:

Площадь круга

В формуле площади (A) круга также используется π:

Вот как использовать эту формулу, чтобы найти приблизительную площадь круга с радиусом 5 мм:

Об этой статье

Эта статья взята из книги:

• Базовая математика и предварительная алгебра для чайников,

Об авторе книги:

Марк Зегарелли — профессиональный писатель со степенями на английском и английском языках. Математика из Университета Рутгерса. Он зарабатывал себе на жизнь в течение многих лет написанием огромного количества логических головоломок, большим количеством документации по программному обеспечению и редкими рецензиями на книги или фильмы. Попутно он также оплатил несколько счетов за уборку дома, декоративную роспись и (в течение десяти часов) розничные продажи.

Хотя больше всего ему нравится писать.

Эту статью можно найти в категории:

• Основы математики,

Как найти диаметр круга

Необходимые определения

Прежде чем научиться находить диаметр круга, необходимо знать следующие определения:

• Диаметр окружности — прямая, проходящая через центр окружности и касающаяся двух противоположных сторон.
• Радиус — прямая линия из центра круга в любую точку по периметру круга.
• Окружность — причудливое слово для периметра или границы круга.
• Площадь круга — общая поверхность круга. Измерение площади всегда будет в квадрате, например, в дюймах2, футах2, м2.
• Центр круга — точка внутри круга, которая находится на одинаковом точном расстоянии от всех точек на периметре круга.
• Пи /∏ — число пи продолжается бесконечно. Для наших целей мы остановимся на слоте 1/100. Для этих расчетов пи будет 3,14.

Вычисление диаметра окружности

Способ определения диаметра окружности зависит от имеющейся информации.

• Если круг нарисован в масштабе или это реальный круг, вы можете рассчитать диаметр, измерив расстояние от одной стороны круга до другой, убедившись, что линейка проходит через центр круга. Поскольку определение точного центра может оказаться трудным, для обеспечения точности лучше всего провести несколько измерений.

• Если вы знаете радиус окружности, умножьте его на 2, чтобы найти диаметр.

  • Если радиус круга равен 2,47 см, диаметр равен 2,47 см * 2, что равно 4,94 см.

• Если вы знаете длину окружности, вы можете разделить ее на пи (3.14), чтобы получить диаметр (длина окружности = пи * диаметр).

• Если вы знаете площадь круга, вы должны изменить формулу площади круга, выполнив следующие действия:

  1. Знать формулу площади круга – Площадь = пи * радиус2 (A=∏r2).
  2. Найдите радиус, разделив обе стороны на 3,14 (пи) и извлекая квадратный корень. Полученная формула: радиус = квадратный корень из площади/пи

  .

  3. Как только вы узнаете площадь, умножьте ее на 2, чтобы получить диаметр.

• Вот пример того, как найти диаметр круга, если известна площадь круга:

  • Если площадь круга равна 12,56 м2, радиус равен квадратному корню из 12,56 м2/3,14. 12,56 м2/3,14=4 м2. Квадратный корень из 4 м2 равен 2 м.
  • Если радиус круга равен 2 метрам, умножьте его на 2, чтобы получить диаметр. Диаметр круга в этом примере равен 4 метрам.

Резюме формулы

• Диаметр = 2 * радиус
• Диаметр = длина окружности / пи
• Диаметр = 2 (квадратный корень из площади/пи)

Теперь вы можете вычислить диаметр круга, если знаете радиус, длину окружности или площадь.

Изображения общественного достояния предоставлены Викискладом.