Шар — это тело, все точки которого находятся от заданой точки на расстоянии, не превышающем R.
Онлайн-калькулятор объема шара
Заданная точка, о которой говорится в определении шара называется центром этого шара. А упомянутое расстояние — радиусом данного шара.
У шара, по аналогии с кругом, так же есть диаметр DD, который по длине в два раза больше радиуса:
D=2⋅RD=2cdot R
Формула объема шара через его радиус
Объем шара вычисляется по следующей формуле:
V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3
RR — радиус данного шара.
Рассмотрим несколько примеров.
Шар вписан в куб, диагональ dd которого равна 500 см.sqrt{500}text{ см.} Найти объем шара.
Решение
d=500d=sqrt{500}
Для начала необходимо определить длину стороны куба. Будем считать, что она равна aa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):
d=a2+a2+a2d=sqrt{a^2+a^2+a^2}
d=3⋅a2d=sqrt{3cdot a^2}
d=3⋅ad=sqrt{3}cdot a
500=3⋅asqrt{500}=sqrt{3}cdot a
a=5003a=sqrt{frac{500}{3}}
a≈12.9aapprox12.9
Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:
R=12⋅aR=frac{1}{2}cdot a
R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4
Заключительный этап — нахождение объема шара по формуле:
V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3
Ответ
1097,5 см3.1097,5text{ см}^3.
Формула объема шара через его диаметр
Так же объем шара можно найти через его диаметр. Для этого используем связь между радиусом и диаметром шара:
D=2⋅RD=2cdot R
R=D2R=frac{D}{2}
Подставим это выражение в формулу для объема шара:
V=43⋅π⋅R3=43⋅π⋅(D2)3=π6⋅D3V=frac{4}{3}cdotpicdot R^3=frac{4}{3}cdotpicdotBig(frac{D}{2}Big)^3=frac{pi}{6}cdot D^3
V=π6⋅D3V=frac{pi}{6}cdot D^3
DD — диаметр данного шара.
Диаметр шара равен 15 см.15text{ см.} Найдите его объем.
Решение
D=15D=15
Сразу подставляем значение диаметра в формулу:
V=π6⋅D3=π6⋅153≈1766.25 см3V=frac{pi}{6}cdot D^3=frac{pi}{6}cdot 15^3approx1766.25text{ см}^3
Ответ
1766.25 см3.1766.25text{ см}^3.
Не знаете, где оформить выполнение контрольных работ на заказ? Профильные эксперты Студворк помогут вам с решением!
Тест по теме «Объем шара»
Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.
Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.
- Диаметр шара через плошадь поверхности шара
- Диаметр шара через обьём шара
Способ вычисления диаметра шара при известном значении объёма фигуры
Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:
D = √(S ⁄ π)
где S — площадь поверхности шара
Цифр после
запятой:
Результат в:
Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.
Способ нахождения диаметра шара при заданном значении его объёма
Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда
D = ³√(6V / π)
где V — объём шара
Цифр после
запятой:
Результат в:
Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.
В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.
Содержание
- – Как вычислить длину шара?
- – Как вычисляется объем шара?
- – Как найти объем шара зная его радиус?
- – Как найти объем прямоугольного параллелепипеда?
- – Как вычислить длину по радиусу?
Диаметр шара, если известен его объем, можно найти используя формулу: D = (6V/пи)^1/3, где V – объем шара. Если известна площадь поверхности шара, то его диаметр можно определить по формуле: D = (S/пи)^1/2, где S – площадь поверхности шара.
Как вычислить длину шара?
C = πD = 2πr. Как и в случае круга, длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
Как вычисляется объем шара?
Формула для вычисления объема шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи. где V – объем шара, R – радиус шара, π = 3.141592.
Как найти объем шара зная его радиус?
Формула вычисления объема шара
- Через радиус Объем (V) шара равняется четырем третьим произведения его радиуса в кубе и числа π.
- Через диаметр Диаметр шара равняется двум его радиусам: d = 2R.
Как найти объем прямоугольного параллелепипеда?
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. – высота.
Как вычислить длину по радиусу?
Радиус равен половине диаметра, а диаметр, соответственно, — двум радиусам (2r). Тогда формула имеет вид: C = 2πr, где C — длина окружности, r — радиус окружности. То есть длина окружности равна удвоенному произведению радиуса на число пи (π примерно равно 3,14).
Интересные материалы:
Как записать трансляцию в прямом эфире?
Как записать загрузочную флешку с образа iso?
Как заполнить форму w 8ben?
Как заполнить массив в Java?
Как запрашивать и отправлять подтверждения прочтения?
Как запросить уведомление о прочтении в майле?
Как запустить игру на видеокарте AMD?
Как запустить интерактивный рендер?
Как запустить команду в командной строке?
Как запустить php скрипт из консоли?
Как узнать диаметр
Диаметр – это линия, которая соединяет две точки криволинейной фигуры и при этом проходит через ее центр. В прикладных задачах часто требуется найти диаметр окружности или шара. Диаметр окружности можно найти по ее радиусу, длине и площади круга. Диаметр шара находят по радиусу, объему и площади поверхности.
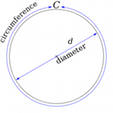
Инструкция
Диаметр окружности или шара, если известны их радиусы, можно найти, зная, что диаметр в два раз превышает радиус. Таким образом, для нахождения диаметра по радиусу, надо величину радиуса умножить на два:
D = 2*R, где R – радиус фигуры.
Диаметр окружности, если известна ее длина, можно найти по формуле:
D = L/пи, где L – длина окружности, пи – постоянная, приблизительно равная 3,14.
Диаметр круга, если известна его площадь, можно найти по формуле:
D = 2*(S/пи)^1/2, где S – площадь круга.
Диаметр шара, если известен его объем, можно найти используя формулу:
D = (6V/пи)^1/3, где V – объем шара.
Если известна площадь поверхности шара, то его диаметр можно определить по формуле:
D = (S/пи)^1/2, где S – площадь поверхности шара.
Обратите внимание
^ – знак, обозначающий возведение в степень;
^1/2 – по сути извлечение квадратного корня;
^1/3 – извлечение кубического корня.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Так как объем шара представляет собой произведение числа π на четыре трети радиуса, возведенного в третью степень, то радиус шара будет равен трем четвертям объема, разделенного на число π, и находящегося под кубическим корнем.
r=∛(3V/4π)=1/2 ∛(3V/π)
Чтобы найти диаметр шара через объем, необходимо удвоить полученное для радиуса выражение, тогда диаметр шара будет равен кубическому корню из отношения утроенного объема к числу π.
d=2r=∛(3V/π)
Вычислить длину окружности сферы через объем можно по стандартной формуле произведения удвоенного радиуса на число π, тогда подставив вместо радиуса выражение через объем сферы, получим кубический корень из произведения квадрата числа π на утроенный объем.
P=2πr=2π 1/2 ∛(3V/π)=∛(3π^2 V)
Площадь поверхности сферы, зная объем, можно найти также, подставив необходимое выражение вместо радиуса сферы, тогда формула будет выглядеть как
S=4πr^2=4π(1/2 ∛(3V/π))^2=∛(36πV^2 )
