Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.
Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
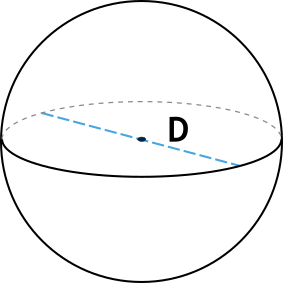
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.
- Диаметр шара через плошадь поверхности шара
- Диаметр шара через обьём шара
Способ вычисления диаметра шара при известном значении объёма фигуры
Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:
D = √(S ⁄ π)
где S — площадь поверхности шара
Цифр после
запятой:
Результат в:
Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.
Способ нахождения диаметра шара при заданном значении его объёма
Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда
D = ³√(6V / π)
где V — объём шара
Цифр после
запятой:
Результат в:
Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.
В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.
Чтобы найти диаметр шара при помощи этого калькулятора, достаточно заполнить любую одну ячейку, введя известное значение, и нажать на кнопку расчета. Программа автоматически вычислит все остальные значения, которые отобразятся в ответе вместе с удобными и понятными формулами.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Радиус (r)
Диаметр (d)
Площадь (S)
Объем (V)
Округление:
Знаков после запятой
* – обязательно заполнить

С помощью этого простого калькулятора можно без труда найти диаметр шара и остальные величины, такие как радиус, площадь и объем шара. Все, что нужно сделать, это заполнить любой один слот и нажать на кнопку “Рассчитать”. В итоге отобразятся все 4 величины вместе с формулами вычисления.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Радиус (r)
Диаметр (d)
Площадь (S)
Объем (V)
Округление:
Знаков после запятой
* – обязательно заполнить
5
2
голоса
Рейтинг статьи
Как узнать диаметр
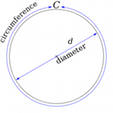
Диаметр – это линия, которая соединяет две точки криволинейной фигуры и при этом проходит через ее центр. В прикладных задачах часто требуется найти диаметр окружности или шара. Диаметр окружности можно найти по ее радиусу, длине и площади круга. Диаметр шара находят по радиусу, объему и площади поверхности.
Инструкция
Диаметр окружности или шара, если известны их радиусы, можно найти, зная, что диаметр в два раз превышает радиус. Таким образом, для нахождения диаметра по радиусу, надо величину радиуса умножить на два:
D = 2*R, где R – радиус фигуры.
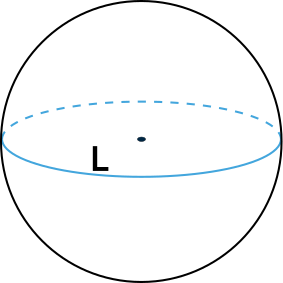
Диаметр окружности, если известна ее длина, можно найти по формуле:
D = L/пи, где L – длина окружности, пи – постоянная, приблизительно равная 3,14.
Диаметр круга, если известна его площадь, можно найти по формуле:
D = 2*(S/пи)^1/2, где S – площадь круга.
Диаметр шара, если известен его объем, можно найти используя формулу:
D = (6V/пи)^1/3, где V – объем шара.
Если известна площадь поверхности шара, то его диаметр можно определить по формуле:
D = (S/пи)^1/2, где S – площадь поверхности шара.
Обратите внимание
^ – знак, обозначающий возведение в степень;
^1/2 – по сути извлечение квадратного корня;
^1/3 – извлечение кубического корня.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус
{V = dfrac{4}{3} pi R^3}
R – радиус шара
Формула объема шара через диаметр
{V = dfrac{1}{6} pi D^3}
D – диаметр шара
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
{V = dfrac{L^3}{6 pi^2}}
L – длина окружности
Формула объема шара через площадь поверхности
{V = sqrt{ dfrac{S^3}{36 pi}}}
S – площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .