Частный
случай полос равной толщины – кольца
Ньютона –
наблюдаются, если плосковыпуклую линзу
поместить на плоскопараллельную
стеклянную пластинку (рис 3).
Если
на линзу падает пучок монохроматического
света, то световые волны, отражённые от
воздуха в точке А
и от стекла в точке В
(т.е. от
верхней и нижней границ воздушной
прослойки), оказываются когерентными
и интерферируют. Волна, отраженная от
плоской поверхности линзы, не когерентна
с ними и дает лишь равномерную засветку.
Точки, для которых толщина воздушного
зазора одинакова, располагаются на
окружностях, поэтому интерференционная
картина имеет вид чередующихся
концентрических темных и светлых колец.

Рис.3. Схема
возникновения колец Ньютона
Так как отражение
световой волны в точке В происходит от
стекла (оптически более плотной среды),
то оптическая длина пути второго луча
в точке А составит АВ + ВА + λ/2. Оптическая
длина пути первого луча в точке А равна
нулю. Поэтому
Δопт
= L2–
L1
= АВ + ВА + λ/2 = 2d
+ λ / 2
Тёмные кольца
образуются там, где оптическая разность
хода равна нечётному числу полуволн:
Δопт
= 2d
+ λ
/2 = (2m
+ 1) λ
/2,
т.е. при толщине
зазора
d
= m
λ
/2 , (8)
где
m
= 0,1,2,3… – номер кольца.
В
центре интерференционной картины
находится темный круг, соответствующий
минимуму нулевого порядка. Если rm
– радиус темного кольца под номером m,
то из треугольника AОС (см. рис.3) имеем:
rm2
=
R2
– (R
– d,)2
= 2Rd
– d
2,
(9)
где
R
– радиус кривизны линзы. Полагая величину
воздушного зазора в месте возникновения
колец малой, (т.е. пренебрегая d
2
по сравнению с 2Rd),
получим:
rm
2 = 2Rd.
.
Подставляя
сюда (8), получим
rm2
= Rmλ
(10)
Из этой формулы
видно, что зная длину волны используемого
света радиус кривизны линзы можно найти
путем измерения радиуса кольца Ньютона
и определения его порядкового номера.
Использование
формулы (10) для определения радиуса
кривизны может привести к ошибке, т.к.
в точке соприкосновения линзы и стеклянной
пластинки возможна деформация, как
линзы, так и пластинки, сравнимая по
величине с длиной волны света. Поэтому
результаты, полученные без учета этого
факта, являются неточными.
Величина
воздушного зазора оказывается меньше
теоретической величины, полученной из
рис.3, на величину суммарной деформации
стеклянной пластинки и линзы δ (рис.4).
Учитывая это, в формулу (9) вместо толщины
воздушного зазора d
необходимо подставить сумму толщины
воздушного зазора и величины суммарной
деформации линзы и стеклянной пластинки
(d
+ δ):
rm2
=
R2
– [R
–(d+
δ)]2.
Пренебрегая
малой величиной (d+
δ)2,
получаем:
rm2
= 2R(d
+ δ
)

Рис.4.
Учет деформации линзы и стеклянной
пластинки
Учитывая
(13), получим следующую формулу, для
радиусов темных колец Ньютона с учетом
суммарной деформации:
rm2
= Rmλ
+ 2Rδ
(11)
Экспериментально
удобнее вместо радиуса кольца Ньютона
измерять его диаметр (Dm
). В этом
случае формула (11) будет иметь вид:
Dm2
= 4Rmλ
+ 8Rδ,
(12)
Из
(12) видно, что квадрат диаметра кольца
Ньютона Dm2
пропорционален порядковому номеру
кольца m.
Если построить график зависимости Dm2
от m,
то экспериментальные точки должны
лежать на одной прямой, и тангенс угла
наклона этой прямой tgα
будет равен 4Rλ.
Таким образом, для нахождения радиуса
кривизны линзы необходимо, используя
график зависимости Dm2
= f(m),
найти
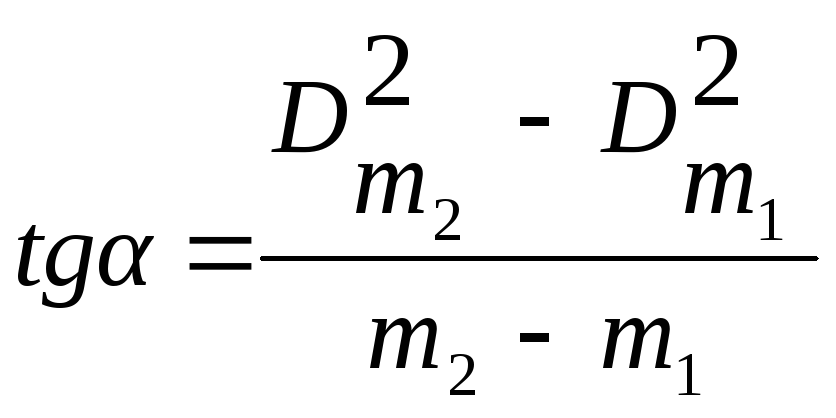 ,
,
(13)
где
m1,
m2
номера колец,
D2m1
и D2m2
– их диаметры,
Радиус кривизны
линзы затем можно рассчитать по формуле
R=tgα/4λ.
(14)
В
центре линзы наблюдается круглое темное
пятно, соответствующее нулевой толщине
воздушного зазора в области деформации.
Измерив диаметр центрального темного
пятна (т.е. темного кольца, номер которого
m=0),
из (12) можно найти величину суммарной
деформации линзы и стеклянной пластинки
по формуле:
δ
= D02/
( 8R
) (15)
Соседние файлы в папке ОПТИКА Лаб.раб 2013
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. Впервые были описаны в 1675 году И. Ньютоном[1].

Описание[править | править код]
Интерференционная картина в виде колец возникает при отражении света от двух поверхностей, одна из которых плоская, а другая имеет относительно большой радиус кривизны и соприкасается с первой (например, стеклянная пластинка и плосковыпуклая линза). Если на такую систему в направлении, перпендикулярном плоской поверхности, падает пучок монохроматического света, то световые волны, отражённые от каждой из упомянутых поверхностей, интерферируют между собой. Сформированная таким образом интерференционная картина состоит из наблюдающегося в месте соприкосновения поверхностей тёмного кружка и окружающих его чередующихся между собой светлых и тёмных концентрических колец[2].
Классическое объяснение явления[править | править код]

Образование тёмных и светлых интерференционных полос в клиновидном воздушном зазоре между двумя стеклянными пластинами. Зазор между поверхностями и длина волны световых волн для наглядности сильно преувеличены.
Во времена Ньютона из-за недостатка сведений о природе света дать полное объяснение механизма возникновения колец было крайне трудно. Ньютон установил связь между размерами колец и кривизной линзы; он понимал, что наблюдаемый эффект связан со свойством периодичности света, но удовлетворительно объяснить причины образования колец удалось лишь значительно позже Томасу Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

Образование колец Ньютона в отражённом (слева) и в проходящем свете (справа)
Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстаёт от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.
— max,
где 

Напротив, если вторая волна отстаёт от первой на нечётное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах, и волны гасят друг друга.
— min,
где 

Для учёта того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода (разность оптических длин пути).
Если 


Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами тёмных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на 
Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:
где 



Радиус k-го тёмного кольца Ньютона в отражённом свете определяется в соответствии с формулой:
Использование[править | править код]
Кольца Ньютона используются для измерения радиусов кривизны поверхностей, для измерения длин волн света и показателей преломления. В некоторых случаях (например, при сканировании изображений на плёнках или оптической печати с негатива) кольца Ньютона представляют собой нежелательное явление.
Используются в физиологии. Подсчёт форменных элементов производится после притирания покровного стекла и камеры Горяева до появления колец Ньютона[3].
Примечания[править | править код]
- ↑ Гагарин А. П. Ньютона кольца // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3 Магнитоплазменный компрессор — Пойнтинга теорема. — С. 370-371. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 115. — 848 с. — ISBN 5-9221-0314-8.
- ↑ Описание сетки камеры Горяева. Дата обращения: 10 июля 2015. Архивировано 3 сентября 2014 года.
Ссылки[править | править код]
 Медиафайлы по теме Кольца Ньютона на Викискладе
Медиафайлы по теме Кольца Ньютона на Викискладе- Фото колец Ньютона в красном монохроматическом свете
- Стрижко А. Н. Определение радиуса кривизны плосковыпуклой линзы с помощью колец Ньютона. Единое окно доступа к образовательным ресурсам. Дата обращения: 3 июня 2011. Архивировано 16 февраля 2012 года.
- Видеоролик с демонстрацией колец Ньютона
Кольца Ньютона
Кольца Ньютона — это кольцевые полосы равной толщины, наблюдаемые при отражении света от поверхностей зазора между стеклянной пластинкой и соприкасающейся с ней выпуклой линзой.
Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельный толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении — эллипсов.

Радиус светлых колец Ньютона в отраженном свете (рис. 1.1, а)
где — номер кольца;
— радиус кривизны линзы;
— длина волны света в вакууме.
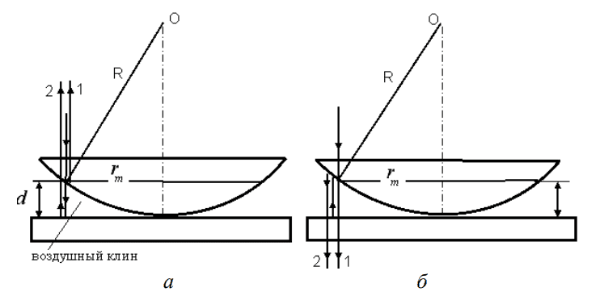
рис. 1.1
Радиус темных колец Ньютона в отраженном свете (рис. 1.1, а)
Радиус светлых колец Ньютона в проходящем свете (рис. 1.1, б)
Радиус темных колец Ньютона в проходящем свете (рис. 1.1, б)
Связь толщины воздушной прослойки с радиусом линзы и радиусом -го кольца Ньютона
Интерференция света от двух когерентных источников света (щели Юнга — рис. 1.2, зеркала и бипризмы Френеля):
-
а) положения последовательных интерференционных максимумов:
-
б) положения последовательных интерференционных минимумов:
-
в) расстояние между соседними максимумами или минимумами:
где — координаты максимумов и минимумов интенсивности ;
— расстояние между источниками света;
— расстояние от источников света до экрана (рис. 1.3).

рис. 1.2
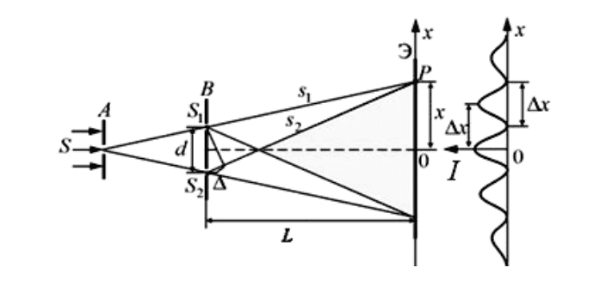
рис. 1.3
Тема: Кольца Ньютона (Прочитано 11511 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Кольца Ньютона образуются между плоским стеклом и линзой с радиусом кривизны R = 8,6 м. Монохроматический свет падает нормально. Измерениями установлено, что диаметр четвертого темного кольца (считая центральное темное пятно за нулевое) равен d = 9 мм. Найти длину волны падающего света. Сделать рисунок.
« Последнее редактирование: 21 Января 2015, 11:55 от Сергей »

Записан
Решение.
Радиус темных колец Ньютона для отраженного света определяется по формуле (формулу принимаем без вывода):
[ {{r}_{k}}=sqrt{kcdot frac{lambda cdot R}{n}}, lambda =frac{r_{k}^{2}cdot n}{kcdot R} (1). ]
Учитываем, что показатель преломления воздуха равен n = 1, r = d/2, r = 4,5∙10-3 м, k = 4.
λ = 5,587∙10-7 м.
« Последнее редактирование: 15 Февраля 2015, 07:23 от alsak »

Записан




