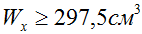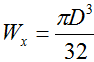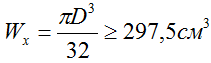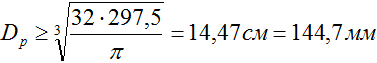Пример решения задачи по подбору минимального диаметра балки круглого поперечного сечения, обеспечивающего её прочность.
Задача
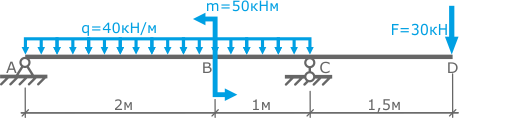
Для заданной стальной балки рассчитать диаметр поперечного сечения по условию прочности.
Полученный размер принять согласно ГОСТ 6636. Допустимые напряжения [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов.
- Расчет момента сопротивления сечения балки по условию прочности.
В предыдущем пункте была рассчитана величина минимально необходимого момента сопротивления сечения балки
С другой стороны момент сопротивления круглого сечения определяется по формуле
таким образом
откуда, расчетный диаметр
Отметим что полученный размер это минимально необходимый диаметр балки, обеспечивающий ее прочность.
Если нет дополнительных условий, то полученный размер можно округлить до целого значения в миллиметрах – 145мм. Округление выполняется исключительно в большую сторону.
По ГОСТ 6636 ближайшее значение в сторону увеличения также составляет 145 мм, его и принимаем за окончательный диаметр балки, т.е. D=145мм.
Оценка экономичности сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Определить диаметры валов сплошного и полого с отношением внутреннего диаметра к наружного. Установить разницу в расходе материала, проверить жесткость валов.
Определить диаметры валов сплошного и полого с отношением внутреннего диаметра к наружного . Установить разницу в расходе материала, проверить жесткость валов. Построить эпюру углов закручивания
для рационального сечения, эпюру касательных напряжений
для сечений, удовлетворяющих условиям прочности и жесткости.
Дано: n = 500 об/мин, Р1 = 90 кВт, Р2 = 80 кВт, Р3 = 60 кВт, Р4 = 50 кВт,
а = 0,1 м, с = 0,3 м, ,
,
.
= 0,75,
2.
Решение
1. Определим величины внешних вращающих моментов по формуле:
М =
кНм,
кНм, аналогично
М3 = 1,15 кНм, М4 = 0,96 кНм.
При равномерном вращении вала алгебраическая сумма внешних моментов равна нулю: М2 + М3 – М1 – М5 – М4 = 0, тогда М5 = 0.
По этим значениям строим эпюру крутящих моментов Мкр. (см. чертеж).
2. Определим диаметр круглого вала из условий прочности при кручении:
90 МПа, где
– полярный момент сопротивления поперечного сечения вала (круга). Тогда
. Отсюда найдем диаметр вала:
м = 46 мм.
Принимаем по ГОСТ 2590-71 d = 46 мм.
Кольцевого поперечного сечения: 

м = 52 мм.
Принимаем по ГОСТ 2590-71 dн = 53 мм, тогда dв = 40 мм.
3. Определим диаметр круглого вала из условий жесткости при кручении.
Условие жесткости при кручении имеет вид:

– угол закручивания на один погонный метр,
– максимальный крутящий момент,
– жёсткость при кручении (
),
– допускаемый угол закручивания на 1 п.м.,
.
Для сплошного вала: 
Тогда найдем диаметр вала из условия жёсткости:
отсюда м = 71 мм.
Принимаем по ГОСТ 2590-71 d = 75 мм.
Для пустотелого вала: 

м = 78 мм.
Принимаем по ГОСТ 2590-71 dн = 80 мм, тогда dв = 60 мм.
Для обеспечения прочности и жесткости вала принимаем сечения большего диаметра: d = 75 мм. Для пустотелого вала: dн = 80 мм, dв = 60 мм. Площади поперечного сечения данных валов будут равны соответственно:
мм2,
мм2.
Окончательно принимаем вал кольцевого поперечного сечения с минимальной площадью, что выгоднее с точки зрения расхода материала при одинаковой нагрузке.
4. Построим эпюру углов закручивания. Для этого определим углы поворота сечений относительно начало отсчета, за которое примем крайнюю левую точку вала – А.
Жесткость вала: =
Нм2
Угол поворота сечения В относительно сечения А равен
рад;
рад;
рад,
рад.
По полученным данным строим эпюру углов закручивания φ (см. чертеж).
5. Построим эпюры распределения касательных напряжений для сечений, удовлетворяющим условиям прочности и жесткости.
Круглое поперечное сечение: d = 75 мм.
=
(75
м)3 = 0,084
м3

Кольцевое поперечное сечение: dн = 80 мм, 0,75
(80
м)3
= 0,070
м3

(80
м)4
= 2,8
м3
МПа.
Рисунок. Эпюры распределения касательных напряжений
Обычно в инженерной
практике проверку прочности балок
производят по нормальным наибольшим и
касательным напряжениям [2]. Нормальные
напряжения σ зависят от величины
изгибавшего момента, а касательные
τ – от величины поперечной силы.
Касательные напряжения в сечениях балки
обычно не играют существенной роли,
поэтому размеры сечения балок определяют
из условия прочности по нормальным
максимальным напряжениям:

где Мmax
–
наибольший (по абсолютной величине)
изгибающий момент, известный из эпюры
изгибающих моментов ().
Сечение балки
подбирается по моменту сопротивления
относительно нейтральной оси:

(3.10)
Для балки
прямоугольного сечения
.
Числовые значения
моментов сопротивления стандартных
профилей проката указаны в соответствующих
государственных стандартах на прокат,
а на балки двутавровые приведены в
таблицах приложения Г. Следует подбирать
номер профиля, имеющий большее стандартное
ближайшее значение. Допустимо принимать
и меньшее ближайшее значение WхСТ,
однако оно должно удовлетворять условию:
.
Момент сопротивления
при изгибе
Подходит швеллер
№ 8 (Wx=22,4
см3,
площадь сечения А=8,98 см2).
Определим
прямоугольное сечение (рисунок 3.10) при
Рисунок 3.10 –
Сечение швеллера и прямоугольное сечение
Площадь
прямоугольного сечения
A=bh=16,27
см2
≈
в 2 раза больше площади швеллера.
3.4 Совместное действие изгиба и кручения
Сочетание деформаций
изгиба и кручения испытывает большинство
валов, которые обычно представляют
собой прямые брусья круглого или
кольцевого сечения.
Возникающие от
изгиба нормальные напряжения достигают
максимального значения в волокнах,
наиболее удаленных от нейтральной оси:
,
где М – максимальный
изгибающий момент, Нм;
W
– осевой момент сопротивления сечения,
м3.
Для вала круглого
сечения
Максимальные
касательные напряжения при кручении
возникают в точках контура поперечного
сечения:
где Wp
– полярный момент сопротивления сечения
(Wp=2W),
м3;
Т
– крутящий момент, Нм.
Таким образом, при
сочетании изгиба и кручения опасными
будут точки (для конкретного поперечного
сечения), наиболее удаленные от нейтральной
оси.
Применив третью
теорию прочности, получим

Расчетная формула
для круглых валов принимает вид:

где М
экв.
– эквивалентный момент, Нм;
[σ]
– допускаемое
напряжение на растяжение для материала
вала, Па.
Если величина и
направление нагрузки во время работы
вращающегося вала остаются неизменными,
то напряжения изгиба в теле вала будут
изменяться во времени по симметричному
циклу – I циклу
нагружения (рисунок 3.11).
Рисунок 3.11 – График
изменения во времени напряжения изгиба
I
цикл
При действии на
вал нагрузок в разных плоскостях силы
раскладывают на две взаимно перпендикулярные
плоскости, за одну из которых выбирают
плоскость действия одной из сил.
Суммарный изгибающий
момент определится как геометрическая
сумма моментов, действующих во взаимно
перпендикулярных плоскостях
рассматриваемого сечения:
где Мiв
и Мiгор
– изгибающие
моменты в i
– м сечении,
действующие в вертикальной и в
горизонтальной плоскостях соответственно.
Эквивалентный
момент определится по формуле:
,
Диаметр вала в
опасном сечении
рассчитывается из условия прочности:

Примечание –
При решении задач все необходимые
вычисления следует сначала проделать
в общем виде, обозначая все данные и
искомые величины буквами, после чего
вместо буквенных обозначений подставить
их числовые значения и найти результат.
На расчетных эскизах размеры должны
быть проставлены теми же буквами, какие
имеются в расчетных формулах.
Пример 4.
Построить
эпюры изгибающих, крутящего, суммарного
изгибающего моментов и определить
диаметр вала (рисунок 3.12) в опасном
сечении.
Т = 0,2 кНм, F
= 2 кН, q
= 4 кН/м, a
= 0,2м, b
=1,2а = 0,24м,
с = 0,8а = 0,16м, [σ]
= 110МПа.
Решение:
Плоскость yz:
Плоскость хz:
Из условия прочности
наиболее нагруженного сечения А определим
диаметр вала.
Рисунок 3.12 –
Расчетная
схема и эпюры вала
ПРИЛОЖЕНИЕ А
ЗАДАЧА 1
Расчет бруса на
осевое растяжение (сжатие)
Сечение бруса
квадратное. Материал – сталь. Допускаемое
напряжение [σ]
= 100 МПа. Модуль продольной упругости Е
= 2·105
МПа. Исходные данные к расчету см. в
таблице + рисунок.
ИСХОДНЫЕ ДАННЫЕ
|
Вариант |
F1 |
F2 |
F3 |
l1 |
l2 |
l3 |
|
кН |
м |
|||||
|
1 |
32 |
18 |
24 |
0,7 |
0,4 |
0,8 |
|
2 |
28 |
16 |
12 |
0,6 |
0,5 |
0,7 |
|
3 |
22 |
8 |
26 |
0,5 |
0,6 |
0,9 |
|
4 |
19 |
24 |
15 |
0,8 |
0,6 |
0,5 |
|
5 |
30 |
12 |
16 |
0,4 |
0,9 |
0,6 |
|
6 |
27 |
15 |
10 |
0,6 |
0,7 |
0,8 |
|
7 |
24 |
14 |
8 |
0,3 |
0,8 |
0,7 |
|
8 |
26 |
16 |
11 |
0,7 |
0,9 |
0,4 |
|
9 |
25 |
12 |
18 |
0,5 |
0,5 |
0,9 |
|
10 |
31 |
26 |
14 |
0,7 |
0,3 |
0,5 |
|
11 |
18 |
15 |
12 |
0,6 |
0,6 |
0,8 |
|
12 |
23 |
25 |
12 |
0,8 |
0,4 |
0,7 |
|
13 |
16 |
8 |
12 |
0,4 |
0,7 |
0,9 |
|
14 |
18 |
10 |
14 |
0,6 |
0,5 |
0,8 |
|
15 |
22 |
12 |
14 |
0,5 |
0,6 |
0,7 |
|
16 |
20 |
9 |
12 |
0,7 |
0,4 |
0,8 |
|
17 |
24 |
16 |
12 |
0,9 |
0,3 |
0,6 |
|
18 |
18 |
10 |
14 |
0,8 |
0,2 |
0,7 |
|
19 |
25 |
18 |
14 |
0,7 |
0,6 |
0,9 |
|
20 |
19 |
11 |
10 |
0,8 |
0,5 |
0,6 |
|
21 |
30 |
13 |
10 |
0,4 |
0,8 |
0,5 |
|
22 |
27 |
15 |
12 |
0,6 |
0,9 |
0,4 |
|
23 |
22 |
11 |
10 |
0,7 |
0,7 |
0,6 |
|
24 |
20 |
9 |
10 |
0,5 |
0,9 |
0,7 |
|
25 |
24 |
12 |
14 |
0,7 |
0,4 |
0,9 |
|
26 |
19 |
10 |
11 |
0,8 |
0,3 |
0,6 |
|
27 |
25 |
13 |
13 |
0,4 |
0,7 |
0,8 |
|
28 |
21 |
16 |
12 |
0,5 |
0,5 |
0,7 |
|
29 |
22 |
20 |
10 |
0,8 |
0,6 |
0,8 |
|
30 |
23 |
15 |
11 |
0,7 |
0,3 |
0,9 |
Расчетные схемы
ПРИЛОЖЕНИЕ Б
ЗАДАЧА 2 РАСЧЕТ
ВАЛА НА КРУЧЕНИЕ
Сечение вала
круглое, сплошное и кольцевое. Допускаемое
напряжение кручения [τ]=25
МПа. Модуль сдвига G=8∙104
МПа
|
Вариант |
Т1, |
Т2, |
Т3, |
Т4, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
200 |
300 |
400 |
0,8 |
0,7 |
0,4 |
0,6 |
0,3 |
|
|
2 |
300 |
500 |
500 |
0,7 |
0,6 |
0,5 |
0,8 |
0,4 |
|
|
3 |
400 |
400 |
300 |
0,9 |
0,5 |
0,6 |
0,3 |
0,2 |
|
|
4 |
100 |
200 |
300 |
0,5 |
0,8 |
0,9 |
0,4 |
0,3 |
|
|
5 |
300 |
400 |
100 |
0,6 |
0,4 |
0,6 |
0,5 |
0,4 |
|
|
6 |
100 |
100 |
500 |
0,8 |
0,6 |
0,7 |
0,3 |
0,2 |
|
|
7 |
300 |
200 |
200 |
0,7 |
0,3 |
0,8 |
0,4 |
0,3 |
|
|
8 |
500 |
600 |
500 |
0,4 |
0,7 |
0,9 |
0,5 |
0,4 |
|
|
9 |
600 |
800 |
700 |
0,9 |
0,5 |
0,5 |
0,3 |
0,2 |
|
|
10 |
400 |
200 |
300 |
0,5 |
0,7 |
0,8 |
0,2 |
0,3 |
|
|
11 |
300 |
500 |
600 |
0,8 |
0,6 |
0,6 |
0,4 |
0,3 |
|
|
12 |
100 |
200 |
200 |
0,7 |
0,8 |
0,4 |
0,3 |
0,4 |
|
|
13 |
700 |
500 |
200 |
0,9 |
0,4 |
0,7 |
0,2 |
0,3 |
|
|
14 |
800 |
400 |
300 |
0,8 |
0,6 |
0,5 |
0,3 |
0,3 |
|
|
15 |
900 |
600 |
400 |
0,7 |
0,5 |
0,6 |
0,4 |
0,4 |
|
|
16 |
100 |
200 |
300 |
0,8 |
0,7 |
0,4 |
0,2 |
0,5 |
|
|
17 |
200 |
800 |
100 |
0,6 |
0,9 |
0,3 |
0,3 |
0,6 |
|
|
18 |
300 |
800 |
100 |
0,7 |
0,8 |
0,2 |
0,4 |
0,7 |
|
|
19 |
400 |
500 |
300 |
200 |
0,9 |
0,7 |
0,6 |
0,2 |
|
|
20 |
500 |
500 |
200 |
300 |
0,6 |
0,8 |
0,5 |
0,3 |
|
|
21 |
600 |
900 |
400 |
100 |
0,5 |
0,4 |
0,8 |
0,4 |
|
|
22 |
700 |
800 |
300 |
200 |
0,4 |
0,6 |
0,9 |
0,2 |
|
|
23 |
800 |
700 |
100 |
400 |
0,6 |
0,7 |
0,7 |
0,3 |
|
|
24 |
900 |
600 |
200 |
300 |
0,7 |
0,5 |
0,9 |
0,4 |
|
|
25 |
100 |
500 |
300 |
200 |
0,9 |
0,7 |
0,4 |
0,2 |
|
|
26 |
200 |
300 |
500 |
300 |
0,6 |
0,8 |
0,3 |
0,4 |
|
|
27 |
300 |
300 |
400 |
200 |
0,8 |
0,4 |
0,7 |
0,3 |
|
|
28 |
400 |
200 |
600 |
100 |
0,7 |
0,5 |
0,5 |
0,2 |
|
|
29 |
500 |
100 |
700 |
200 |
0,8 |
0,8 |
0,6 |
0,3 |
|
|
30 |
600 |
200 |
800 |
300 |
0,9 |
0,7 |
0,3 |
0,4 |
Расчетные схемы
ПРИЛОЖЕНИЕ В
ЗАДАЧА 3
РАСЧЕТ НА ПРОЧНОСТЬ ДВУХОПОРНОЙ БАЛКИ
ПРИ ИЗГИБЕ
Для данной балки подобрать сечения
двутавра и прямоугольника (h/b=2).
Допускаемое напряжения изгиба [σ]=160
МПа
|
Вариант |
М,K |
F, |
q, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
18 |
26 |
14 |
2 |
2 |
5 |
1 |
1 |
|
2 |
24 |
18 |
10 |
2 |
3 |
2 |
3 |
2 |
|
3 |
16 |
34 |
12 |
2 |
3 |
3 |
2 |
2 |
|
4 |
30 |
24 |
16 |
2 |
4 |
4 |
1 |
2 |
|
5 |
20 |
12 |
8 |
1,8 |
2,2 |
1 |
5 |
1 |
|
6 |
22 |
16 |
10 |
1,6 |
1 |
1,4 |
6 |
2 |
|
7 |
18 |
22 |
14 |
2,2 |
2 |
1,8 |
5 |
1 |
|
8 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
9 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
10 |
14 |
15 |
8 |
1,6 |
2 |
1,4 |
4 |
3 |
|
11 |
10 |
23 |
12 |
2 |
2 |
2 |
4 |
2 |
|
12 |
18 |
17 |
10 |
1,8 |
3 |
1,2 |
5 |
1 |
|
13 |
16 |
25 |
15 |
2 |
2 |
4 |
2 |
2 |
|
14 |
24 |
16 |
10 |
2 |
3 |
4 |
2 |
1 |
|
15 |
1 |
22 |
12 |
1,6 |
2,4 |
3,5 |
2,5 |
2 |
|
16 |
20 |
18 |
14 |
1,8 |
2,2 |
4,5 |
2,5 |
2 |
|
17 |
22 |
24 |
8 |
2 |
2 |
4 |
3 |
1 |
|
18 |
16 |
26 |
6 |
2 |
2 |
3,5 |
3,5 |
1 |
|
19 |
18 |
20 |
10 |
1,5 |
2,5 |
4,2 |
1,8 |
8 |
|
20 |
28 |
18 |
16 |
1,8 |
2,2 |
4,5 |
2,5 |
3 |
|
21 |
17 |
25 |
12 |
2 |
2 |
1 |
5 |
2 |
|
22 |
15 |
30 |
10 |
1,5 |
2,5 |
2 |
4 |
1 |
|
23 |
26 |
22 |
8 |
2 |
2 |
2 |
3 |
2 |
|
24 |
30 |
18 |
14 |
1,6 |
3,0 |
2 |
4 |
1 |
|
25 |
24 |
26 |
15 |
1,5 |
2,5 |
6 |
1 |
1 |
|
26 |
22 |
13 |
2,5 |
1,5 |
5 |
2 |
2 |
|
|
27 |
20 |
12 |
2,0 |
1,5 |
5,5 |
3 |
2 |
|
|
28 |
18 |
28 |
10 |
2,0 |
1,5 |
4,5 |
2 |
2 |
|
29 |
30 |
20 |
8 |
1,8 |
3,2 |
1 |
2 |
1 |
|
30 |
28 |
18 |
15 |
2 |
2,5 |
1,5 |
5 |
2 |
Расчетные схемы
задачи 3
ПРИЛОЖЕНИЕ Г
Сталь прокатная
– балки двутавровые (ГОСТ 8239-83)
h
– высота профиля;
b
– ширина;
d
– толщина;
t
– средняя толщина;
R
и r
– внутренний и наружный радиусы
скруглений;
J
– момент инерции;
W
– момент сопротивления;
i
– радиус инерции;
S
– статический момент полусечения
|
Номер профиля |
Масса |
Размеры, |
Площадь сечения, |
Jx, см4 |
Wx, см3 |
ix, см |
Sx, см3 |
Jy, см4 |
Wy, см3 |
iy, см |
|||||
|
h |
b |
d |
t |
R |
r |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
10 |
9,46 |
100 |
55 |
4,5 |
7,2 |
7 |
2,5 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
11,45 |
120 |
64 |
4,8 |
7,3 |
7,5 |
3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
13,7 |
140 |
73 |
4,9 |
7,5 |
8 |
3 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
15,9 |
160 |
81 |
5,0 |
7,8 |
8,5 |
3,5 |
20,2 |
873 |
109,0 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
18,4 |
180 |
90 |
5,1 |
8,1 |
9,0 |
3,5 |
23,4 |
1290 |
143,0 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
18а |
19,9 |
180 |
100 |
5,1 |
8,3 |
9,0 |
3,5 |
25,4 |
1430 |
159,0 |
7,51 |
89,8 |
114,0 |
22,8 |
2,12 |
|
20 |
21,0 |
200 |
100 |
5,2 |
8,4 |
9,5 |
4,0 |
26,8 |
1840 |
184,0 |
8,28 |
104,0 |
115,0 |
23,1 |
2,07 |
|
20а |
22,7 |
200 |
110 |
5,2 |
8,6 |
9,5 |
4,0 |
28,9 |
2030 |
203,0 |
8,37 |
114,0 |
155,0 |
28,2 |
2,32 |
|
22 |
24,0 |
220 |
110 |
5,4 |
8,7 |
10,0 |
4,0 |
30,6 |
2550 |
232,0 |
9,13 |
131,0 |
157,0 |
28,6 |
2,27 |
|
22а |
25,8 |
220 |
120 |
5,4 |
8,9 |
10,0 |
4,0 |
32,6 |
2790 |
254,0 |
9,22 |
143,0 |
106,0 |
34,3 |
2,5 |
|
24 |
27,3 |
240 |
115 |
5,6 |
9,5 |
10,5 |
4,0 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
24а |
29,4 |
240 |
125 |
5,6 |
9,8 |
20,5 |
4,0 |
37,5 |
3800 |
317 |
10,1 |
178 |
260 |
41,6 |
2,63 |
|
27 |
31,5 |
270 |
125 |
6,0 |
9,8 |
11,0 |
4,5 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
27а |
33,9 |
270 |
135 |
6,0 |
10,2 |
11,0 |
4,5 |
43,2 |
5500 |
407 |
11,3 |
229 |
337 |
50,0 |
2,8 |
|
30 |
36,5 |
300 |
135 |
6,5 |
10,2 |
12,0 |
5 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
30а |
39,2 |
300 |
145 |
6,5 |
10,7 |
12,0 |
5 |
49,9 |
7780 |
518 |
12,5 |
292 |
436 |
60,1 |
2,95 |
|
33 |
42,2 |
330 |
140 |
7,0 |
11,2 |
13,0 |
5 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,1 |
3,79 |
|
36 |
48,6 |
360 |
145 |
7,5 |
12,3 |
14,0 |
6 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
57,0 |
400 |
155 |
8,3 |
13,0 |
15,0 |
6 |
72,6 |
19062 |
953 |
16,2 |
545 |
667 |
86,1 |
3,08 |
|
45 |
66,5 |
450 |
160 |
9,0 |
14,2 |
16,0 |
7 |
84,7 |
27696 |
1231 |
18,1 |
708 |
808 |
101,0 |
3,09 |
|
50 |
78,5 |
500 |
170 |
10,0 |
15,2 |
17,0 |
7 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123,0 |
3,23 |
|
60 |
108,0 |
600 |
190 |
12,0 |
17,8 |
20,0 |
8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182,0 |
3,54 |
|
60б |
120,0 |
650 |
200 |
12,0 |
19,2 |
22,0 |
9 |
153 |
101400 |
3120 |
25,8 |
1800 |
2170 |
217,0 |
3,77 |
|
70 |
138,0 |
700 |
210 |
13,0 |
20,8 |
24,0 |
10 |
176 |
134600 |
3840 |
27,7 |
2230 |
2730 |
260,0 |
3,94 |
|
70а |
168,0 |
700 |
210 |
15,0 |
24,0 |
24,0 |
10 |
202 |
152700 |
4360 |
27,5 |
2550 |
3240 |
309,0 |
4,01 |
|
70б |
184,0 |
700 |
210 |
17,5 |
28,2 |
24,0 |
10 |
234 |
175770 |
5010 |
27,4 |
2940 |
3910 |
373,0 |
4,09 |
ПРИЛОЖЕНИЕ Д
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти ядро сечения в сопромате
При конструировании стержней из материалов, плохо сопротивляющихся растяжению (бетон), весьма желательно добиться того, чтобы все сечение работало лишь на сжатие. Этого можно достигнуть, не давая точке приложения силы Р слишком далеко отходить от центра тяжести сечения, ограничивая величину эксцентриситета.
Конструктору желательно заранее знать, какой эксцентриситет при выбранном типе сечения можно допустить, не рискуя вызвать в сечениях стержня напряжений разных знаков. Здесь вводится понятие о так называемом ядре сечения. Этим термином обозначается некоторая область вокруг центра тяжести сечения, внутри которой можно располагать точку приложения силы Р, не вызывая в сечении напряжений разного знака.
Пока точка А располагается внутри ядра, нейтральная ось не пересекает контура сечения, все оно лежит по одну сторону от нейтральной оси и, стало быть, работает лишь на сжатие. При удалении точки А от центра тяжести сечения нейтральная ось будет приближаться к контуру; граница ядра определится тем, что при расположении точки А на этой границе нейтральная ось подойдет вплотную к сечению, коснется его.
Рис.1. Комбинации положения сжимающей силы и нейтральной линии
Таким образом, если мы будем перемещать точку А так, чтобы нейтральная ось катилась по контуру сечения, не пересекая его, то точка А обойдет по границе ядра сечения. Если контур сечения имеет «впадины», то нейтральная ось будет катиться по огибающей контура.
Чтобы получить очертание ядра, необходимо дать нейтральной оси несколько положений, касательных к контуру сечения, определить для этих положений отрезки 



это и будут координаты точек контура ядра 

При многоугольной форме контура сечения (Рис.2), совмещая последовательно нейтральную ось с каждой из сторон многоугольника, мы по отрезкам 



При переходе от одной стороны контура сечения к другой нейтральная ось будет вращаться вокруг вершины, разделяющей эти стороны; точка приложения силы будет перемещаться по границе ядра между полученными уже точками. Установим, как должна перемещаться сила Р, чтобы нейтральная ось проходила все время через одну и ту же точку В (

Рис.2. Ядро сечения для многоугольной формы поперечного сечения
Таким образом координаты 


На Рис.3 изображены три положения точки приложения силы на этой прямой и соответственно три положения нейтральной оси. Таким образом, при многоугольной форме контура сечения очертание ядра между точками, соответствующими сторонам многоугольника, будет состоять из отрезков прямых линий.
Рис.3. Динамика построения ядра сечения
Если контур сечения целиком или частично ограничен кривыми линиями, то построение границы ядра можно вести по точкам. Рассмотрим несколько простых примеров построения ядра сечения.
При выполнении этого построения для прямоугольного поперечного сечения воспользуемся полученными формулами.
Для определения границ ядра сечения при движении точки А по оси Оу найдем то значение 
Таким образом, границы ядра по оси Оу будут отстоять от центра сечения на 1/6 величины b (Рис.4, точки 1 и 3); по оси Oz границы ядра определятся расстояниями 
Для получения очертания ядра целиком изобразим положения нейтральной оси 

При перемещении силы из точки 1 в точку 2 по границе ядра нейтральная ось должна перейти из положения 

Рис.4. построение ядра для прямоугольного сечения.
Для этого сила должна двигаться по прямой 1 2. Точно так же можно доказать, что остальными границами ядра будут линии 23, 34 и 41.
Таким образом, для прямоугольного сечения ядро будет ромбом с диагоналями, равными одной трети соответствующей стороны сечения. Поэтому прямоугольное сечение при расположении силы по главной оси работает на напряжения одного знака, если точка приложения силы не выходит за пределы средней трети стороны сечения.
Рис.5. Динамика изменения напряжений при изменении эксцентриситета.
Эпюры распределения нормальных напряжений по прямоугольному сечению при эксцентриситете, равном нулю, меньшем, равном и большем одной шестой ширины сечения, изображены на Рис.5.
Отметим, что при всех положениях силы Р напряжение в центре тяжести сечения (точка О) одинаково и равно 
Для круглого сечения радиуса r очертание ядра будет по симметрии кругом радиуса 

Рис.6. Ядро сечения для двутавра а) и швеллера б)
Таким образом, ядро представляет собой круг с радиусом, вчетверо меньшим, чем радиус сечения.
Для двутавра нейтральная ось при обходе контура не будет пересекать площади поперечного сечения, если будет касаться прямоугольного контура ABCD, описанного около двутавра (Рис.6а). Следовательно, очертание ядра для двутавра имеет форму ромба, как и для прямоугольника, но с другими размерами.
Для швеллера, как и для двутавра, точки 1, 2, 3, 4 контура ядра (Рис.6 б) соответствуют совпадению нейтральной оси со сторонами прямоугольника ABCD.
Источник
Голосование за лучший ответ
А.УМАРОВ
Оракул
(70014)
9 лет назад
Этого недостаточно для расчета. Нет схемы нагружения, из которой можно судить о моменте и характере нагрузки (изгиб, кручение, сжатие или растяжение)
ВК
Просветленный
(32923)
9 лет назад
F/A=сигма<10 -условие прочности, отсюда находите площадь А, потом диаметр. Только внимательно с размерностями, все перевести в СИ.