Как найти диаметр зная площадь сферы

Вы здесь

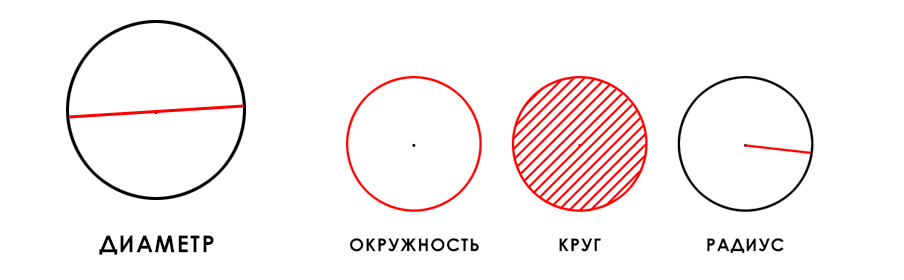
Диаметр

Диаметр круга или сферы – это хорда или линия, соединяющая две точки окружности, и проходящая через центр круга. Таким образом, диаметр – это два радиуса, расположенных по отношению друг к другу под углом 180°, так чтобы получить прямую линию.

Диаметр круга

Диаметр круга напрямую связан с радиусом и представляет собой его удвоенное значение. Но это не единственный способ вычислить диаметр. Зная площадь круга, можно конвертировать формулу, подставив вместо радиуса половину диаметра, и вывести значение последнего:

Точно также можно найти диаметр круга через длину окружности, разделив ее на 4π:

Диаметр сферы

Диаметр сферы – это точно такой же удвоенный радиус, как и диаметр круга. По сути, диаметр представляет собой ось вращения сферы, поэтому он напрямую связан с ее размерами. Помимо радиуса и диаметра, у сферы есть определенный объем, который она занимает в пространстве. Связь объема с диаметром выражается следующим образом:

Также вычислить диаметр сферы можно через ее площадь. Исходя из формулы площади сферы или шара следует, что его поверхность описывается произведением числа π на квадрат диаметра. Следовательно, диаметр сферы через ее площадь, трансформируя эту формулу, можно получить через извлечение квадратного корня из отношения площади сферы к числу π.

Смотрите также

Источник

Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.

Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.

Диаметр шара через плошадь поверхности шара
Диаметр шара через обьём шара

Способ вычисления диаметра шара при известном значении объёма фигуры

Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:

D = √(S ⁄ π)

где S — площадь поверхности шара

Цифр после
запятой:

Результат в:

Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.

Способ нахождения диаметра шара при заданном значении его объёма

Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда

D = ³√(6V / π)

где V — объём шара

Цифр после
запятой:

Результат в:

Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.

В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.

Источник

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

Что такое диаметр круга?

Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.

Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.

Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).

Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.

Формулы определения диаметра круга

Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.

По радиусу

Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.

d = r × 2

Где d – это диаметр, а r – радиус.

По длине окружности

Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.

d = L / π

Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.

Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).

Через площадь круга

Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр. Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:

d = 2 × (S/π)^1/2

Где d – диаметр, S – площадь круга, а π – константа, которая примерно равна 3,14.

То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.

Примеры вычисления диаметра

Давайте для закрепления рассмотрим несколько примеров.

Пример 1. Диаметр по длине окружности трубы 🚿

Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).

А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:

d = 31,4 / 3,14 = 10 см.

Это и есть правильный ответ – 10 сантиметров.

Пример 2. Диаметр по колеса радиусу 🚲

Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?

Диаметру будет равен двум радиусам, то есть 20 дюймов.

Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.

❓Вопросы и ответы

И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.

Как работает ваш онлайн-калькулятор?

Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.

Достаточно ли у меня данных для расчёта?

Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Если у автомобильного колеса параметр R16, то какой у него диаметр?

16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.

Диаметр сферы с учетом площади поверхности Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Площадь поверхности сферы: 1300 Квадратный метр –> 1300 Квадратный метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

20.3421447256411 метр –> Конверсия не требуется

5 Диаметр сферы Калькуляторы

Диаметр сферы с учетом площади поверхности формула

Диаметр сферы = sqrt(Площадь поверхности сферы/pi)

D = sqrt(SA/pi)

Что такое Сфера?

Сфера — это замкнутая и симметричная трехмерная форма, состоящая из всех точек, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром сферы, а фиксированное расстояние называется радиусом сферы. Сферы — это трехмерное расширение кругов в двух измерениях.

Источник

Чтобы найти диаметр шара при помощи этого калькулятора, достаточно заполнить любую одну ячейку, введя известное значение, и нажать на кнопку расчета. Программа автоматически вычислит все остальные значения, которые отобразятся в ответе вместе с удобными и понятными формулами.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Радиус (r)

Диаметр (d)

Площадь (S)

Объем (V)

Округление:

Знаков после запятой

* – обязательно заполнить

Источник

Вы здесь

Диаметр

Диаметр круга