Как рассчитать радиус и диаметр овала
Овал также называют эллипсом. Из-за своей продолговатой формы овал имеет два диаметра: диаметр, который проходит через самую короткую часть овала, или полу-малую ось, и диаметр, который проходит через

Содержание:
Овал также называют эллипсом. Из-за своей продолговатой формы овал имеет два диаметра: диаметр, который проходит через самую короткую часть овала, или полу-малую ось, и диаметр, который проходит через самую длинную часть овала, или полу-большую ось. , Каждая ось перпендикулярно делит пополам другую, разрезая друг друга на две равные части и создавая прямые углы там, где они встречаются. Есть также два радиуса, по одному на каждый диаметр. Чтобы рассчитать радиусы и диаметры или оси овала, используйте точки фокусировки овала – две точки, которые расположены на равном расстоянии друг от друга на большой полуоси – и любую одну точку по периметру овала.
Полу минорная ось
Измерьте расстояние между одной точкой фокусировки до точки по периметру овала, чтобы определить a. В этом примере a будет равно 5 см.
Измерьте расстояние между другой точкой фокусировки и той же точкой на периметре, чтобы определить b. В этом примере b будет равен 3 см.
Добавьте a и b вместе и возведите в квадрат сумму. Например, 5 см плюс 3 см равны 8 см, а 8 см в квадрате равны 64 см ^ 2.
Измерьте расстояние между двумя точками фокусировки, чтобы выяснить f; возвести в квадрат результат. В этом примере f равно 5 см, а квадрат 5 см равен 25 см ^ 2.
Вычтите сумму на шаге четыре из суммы на шаге три. Например, 64 см ^ 2 минус 25 см ^ 2 равняется 39 см ^ 2.
Рассчитайте квадратный корень суммы из шага пять. Например, квадратный корень из 39 равен 6,245, округленный до ближайшей тысячной. Следовательно, малая ось или самый короткий диаметр составляет 6,245 см.
Разделите измерение полу-малой оси пополам, чтобы вычислить ее радиус. Например, 6,245 см, разделенные на два, равны 3,122 см.
Полу-Большая Ось
Повторите процесс измерения из предыдущего раздела, чтобы выяснить a и b. В этом примере хорошо использовать те же цифры: 5 см и 3 см.
Добавьте a и b вместе. Результатом является большая полуось. Например, 5 см плюс 3 см равны 8 см, поэтому большая полуось составляет 8 см.
Уменьшить вдвое результат первого шага, чтобы вычислить радиус. Восемь, разделенная на два, равна четырем, поэтому другой радиус равен 4 см.
Калькулятор периметра эллипса
Введите длину большой и малой полуосей эллипса, укажите точность расчета и нажмите “Посчитать”. Калькулятор выполнит расчет периметра эллипса (расчет приблизительный).
Калькулятор
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости есть величина постоянная, больше расстояния между F1 и F2.
Точки F1 и F2 называют фокусами эллипса, а расстояние между ними – фокусным расстоянием.
Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a.
Отрезок, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Формулу периметра эллипса нельзя выразить при помощи простейших функций.
Как посчитать диаметр окружности
Онлайн калькулятор
Как посчитать диаметр зная длину окружности
Чему равен диаметр если длина окружности ?
Каков диаметр (d) если длина окружности C?
Формула
d = C /π , где π ≈ 3.14
Пример
Если длина круга равна 5 см, то его диаметр примерно равен 1.59 см.
Как посчитать диаметр зная радиус окружности
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её радиус r?
Формула
Пример
Если радиус круга равен 0.5 см, то его диаметр равен 1 см.
Как посчитать диаметр окружности зная её площадь
Чему равен диаметр окружности если
Каков диаметр окружности (d) если её площадь S?
Формула
d = √ 4S /π , где π ≈ 3.14
Пример
Если площадь круга равна 5 см 2 , то его диаметр примерно равен 2.52 см.
[spoiler title=”источники:”]
http://fin-calc.org.ua/ru/calculator/geometry/perimeter/ellipse/
http://poschitat.online/diametr-okruzhnosti
[/spoiler]
An oval is also referred to as an ellipse. Because of its oblong shape, the oval features two diameters: the diameter that runs through the shortest part of the oval, or the semi-minor axis, and the diameter that runs through the longest part of the oval, or the semi-major axis. Each axis perpendicularly bisects the other, cutting each other into two equal parts and creating right angles where they meet. There are also two radii, one for each diameter. To calculate the radii and diameters, or axes, of the oval, use the focus points of the oval — two points that lie equally spaced on the semi-major axis — and any one point on the perimeter of the oval.
The Semi-Minor Axis
Measure the distance between one focus point to the point on the oval’s perimeter to determine a. In this example, a will equal 5 cm.
Measure the distance between the other focus point to that same point on the perimeter to determine b. In this example, b will equal 3 cm.
Add a and b together and square the sum. For example, 5 cm plus 3 cm equals 8 cm, and 8 cm squared equals 64 cm^2.
Measure the distance between the two focus points to figure out f; square the result. In this example, f equals 5 cm, and 5 cm squared equals 25 cm^2.
Subtract the sum in step four from the sum in step three. For example, 64 cm^2 minus 25 cm^2 equals 39 cm^2.
Calculate the square root of the sum from step five. For example, the square root of 39 equals 6.245, rounded to the nearest thousandth. Therefore, the semi-minor axis, or shortest diameter, is 6.245 cm.
Divide the semi-minor axis measurement in half to figure its radius. For example, 6.245 cm divided by two equals 3.122 cm.
The Semi-Major Axis
- Ruler
- Calculator
Repeat the measuring process from the previous section to figure out a and b. In this example, we’ll use the same numbers: 5 cm and 3 cm.
Add a and b together. The result is the semi-major axis. For example, 5 cm plus 3 cm equals 8 cm, so the semi-major axis is 8 cm.
Halve the result from step one to figure the radius. Eight divided by two equals four, so the other radius is 4 cm.
Things You’ll Need
Макеты страниц
Все диаметры эллипса проходят через его центр. Диаметр, соответствующий хордам, параллельным малой оси, есть большая ось (рис. 76). Диаметр, соответствующий хордам, параллельным большой оси, есть малая ось.
Хордам с угловым коэффициентом  отвечает диаметр
отвечает диаметр  где
где  определяется из соотношения
определяется из соотношения

т. е.

Пример 1. Диаметр  эллипса
эллипса  (рис. 77), отвечающий хордам с угловым коэффициентом
(рис. 77), отвечающий хордам с угловым коэффициентом  представляется
представляется

Рис. 101

Рис. 72
уравнением  значение
значение  определяется из соотношения
определяется из соотношения  так что уравнение диаметра
так что уравнение диаметра 
Пример 2. Диаметр  (см. рис. 77) того же эллипса, соответствующий хордам с угловым коэффициентом
(см. рис. 77) того же эллипса, соответствующий хордам с угловым коэффициентом  представляется уравнением
представляется уравнением 
Если диаметр  эллипса делит пополам хорды, параллельные диаметру
эллипса делит пополам хорды, параллельные диаметру  , то диаметр
, то диаметр  всегда делит пополам хорды, параллельные диаметру
всегда делит пополам хорды, параллельные диаметру 
Пример 3. Диаметр  эллипса
эллипса  (ср. примеры 1 и 2) делит пополам хорды, параллельные диаметру
(ср. примеры 1 и 2) делит пополам хорды, параллельные диаметру  В свою очередь диаметр
В свою очередь диаметр  делит пополам хорды, параллельные диаметру
делит пополам хорды, параллельные диаметру 
Диаметры, каждый из которых делит пополам хорды, параллельные другому, называются взаимно сопряженными.
Два диаметра, сопряженных друг с другом и вместе с тем взаимно перпендикулярных, называются главными диаметрами. У окружности всякий диаметр — главный. У эллипса, отличного от окружности, есть лишь одна пара главных диаметров — большая и малая оси.
Угловые коэффициенты неглавных сопряженных направлений имеют согласно соотношению (1а) противоположные знаки, т. е. два сопряженных диаметра эллипса принадлежат различным парам вертикальных углов, образуемых осями (на рис. 77 диаметр  лежит во II и IV четверти, а
лежит во II и IV четверти, а  в I и III четверти). При вращении диаметра
в I и III четверти). При вращении диаметра  сопряженный диаметр
сопряженный диаметр  вращается в ту же сторону, что и
вращается в ту же сторону, что и 
Как рассчитать радиус и диаметр овала
Овал также называют эллипсом. Из-за своей продолговатой формы овал имеет два диаметра: диаметр, который проходит через самую короткую часть овал, или малая полуось, и диаметр, проходящий через самую длинную часть овала, или большую полуось. Каждая ось перпендикулярно делит другую пополам, разделяя друг друга на две равные части и создавая прямые углы в местах их пересечения. Также есть два радиуса, по одному на каждый диаметр. Чтобы вычислить радиусы и диаметры или оси овала, используйте точки фокусировки овала – две точки, которые лежат на равном расстоянии от большой полуоси – и любая точка по периметру овал.
Измерьте расстояние между одной точкой фокусировки и точкой по периметру овала, чтобы определить a. В этом примере a будет равно 5 см.
Измерьте расстояние между другой точкой фокусировки и той же точкой по периметру, чтобы определить b. В этом примере b будет равно 3 см.
Сложите a и b и возведите сумму в квадрат. Например, 5 см плюс 3 см равняется 8 см, а 8 см в квадрате равняется 64 см ^ 2.
Измерьте расстояние между двумя точками фокусировки, чтобы вычислить f; возведите результат в квадрат. В этом примере f равно 5 см, а квадрат 5 см равен 25 см ^ 2.
Вычтите сумму на четвертом шаге из суммы на третьем. Например, 64 см ^ 2 минус 25 см ^ 2 равно 39 см ^ 2.
Вычислите квадратный корень из суммы, полученной на пятом шаге. Например, квадратный корень из 39 равен 6,245 с округлением до ближайшей тысячной. Следовательно, малая полуось, или самый короткий диаметр, составляет 6,245 см.
Разделите размер малой полуоси пополам, чтобы определить ее радиус. Например, 6,245 см, разделенное на два, равно 3,122 см.
Teachs.ru
- Доля
Перейти к содержанию
Длина эллипса (овала)
На чтение 1 мин
Эллипс – это множество точек плоскости, для которых сумма расстояний до фокусов эллипса постоянна и больше расстояния между фокусами.
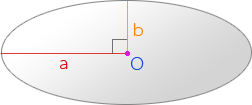 a, b – полуоси эллипса
a, b – полуоси эллипса
О – центр эллипса
Длина эллипса (L) равна произведению суммы его полуосей (a, b) на число π:

Вам также может понравиться
Дуга – это часть окружности, отсекаемая хордой.
0139
Окружность – геометрическое место точек, равноудаленных
0122

Окружность – геометрическое место точек, равноудаленных
0121
Многоугольник – это геометрическая фигура, которая
0137
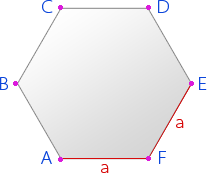
Шестиугольник – это многоугольник, который имеет шесть углов.
0422
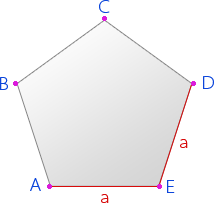
Пятиугольник – это многоугольник, который имеет пять углов.
0318
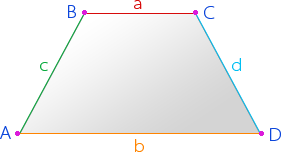
Трапеция – это четырехугольник, у которого параллельна
087
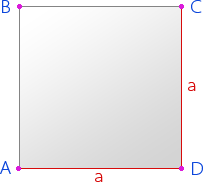
Квадрат – это параллелограмм, у которого все углы и
089
