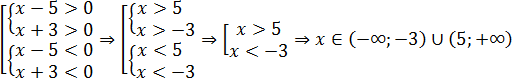Как найти диапазон математика

Описание изображения

Вид на пустую аудиторию колледжа с задней стороны.

Для любого человека, заинтересованного в карьере математика или человека, который использует математику, например, в бизнесе, важно уметь четко объяснять формулы и решения. В случае нахождения диапазона функции, вы можете найти это значение несколькими способами. Умение объяснить эти методы может оказаться полезным по мере развития ваших математических и коммуникативных навыков.

В этой статье мы дадим определение математического диапазона, области и функции, а затем расскажем, как найти диапазон функции с помощью формулы, графика и отношения.

Основные выводы:

• В математике функция представляет собой определенную связь между независимой переменной (x) и зависимой переменной (y).

• Диапазон функции относится ко всем возможным значениям y.

• Формула для нахождения диапазона функции: y = f(x). Отношение является функцией только в том случае, если каждому значению x соответствует только одно значение y.

Что такое функция?

Функция – это прикладной математический термин, используемый для описания взаимосвязи между двумя переменными. В формуле вы можете представить функцию в виде:

y = f(x)

В этой формуле y является функцией x, то есть при изменении значения x изменяется и значение y (или диапазон, или зависимая переменная). Например:

Если x равен 2 в уравнении y = x -1, то значение y равно 1: y = 2-1

Но если x имеет значение 10, то y также изменится – до 9, или y=10-1

Что такое диапазон функции?

Значения переменных меняются, что можно представить в виде набора значений, называемых областью и диапазоном функции:

• Домен: Область функции – это набор чисел, представляющих все значения, которые может иметь x.

• Диапазон: Диапазон – это набор чисел, которые представляют все потенциальные значения, которые y может иметь на основе функции.

3 способа найти диапазон функции

Для x в упорядоченной паре (x, y) может соответствовать только одно значение y. Для y, однако, существует больше возможностей. Нахождение диапазона функции означает нахождение всех возможных значений, которые может иметь y в зависимости от x. Вы можете найти диапазон функции тремя способами: формула, график или зависимость.

1. Нахождение диапазона функции с помощью формулы

Формула может представлять, как переменная x взаимодействует с переменной y. Эти формулы могут выглядеть по-разному в зависимости от того, какое взаимодействие имеют значения. Ниже приведены шаги, которые можно использовать для алгебраического нахождения диапазона функции:

1. Запишите формулу

Запись формулы – где y = f(x)- может помочь вам определить некоторые аспекты связи между двумя переменными.

Пример: Если вы продаете журналы по 10 долларов за штуку, то ваш общий объем продаж, f(x), равен количеству проданных журналов, x, умноженному на 10. Итак, формула f(x) = 10(x). Если вы продаете ноль, 2, 4 или 10 журналов, то ваши общие продажи составляют $0, $20, $40 и $100.

2. Найдите другие пары координат

Если применить формулу y = f(x), то она показывает положительную зависимость между x и y для всех журналов продаж. Чтобы перепроверить эту информацию, вы можете нарисовать переменные в виде упорядоченных пар на графике. Полученный график является линейным и имеет тенденцию к росту. Это подтверждает вывод о том, что функция положительна.

3. Напишите диапазон

Зная, что вы не можете продавать отрицательные журналы, вы можете определить, что диапазон функции никогда не бывает меньше нуля. Поскольку вы всегда можете продать больше журналов, вы знаете, что диапазон может постоянно увеличиваться на интервалы в 10 раз. Таким образом, вы можете записать диапазон функции в виде эквивалентности.

В данном примере диапазон f(x) = все кратные 10 ? 0.

2. Нахождение диапазона функции с помощью графика

График может обеспечить визуальное представление формы, которую принимает функция, позволяя увидеть, как координаты y взаимодействуют с координатами x. Вот шаги для нахождения диапазона функции с помощью графика:

1. Нарисуйте функцию на графике

Чтобы найти диапазон функции на графике, отметьте (или постройте) координаты области (x) и диапазона (y) на листе бумаги с помощью маленьких точек. Это поможет вам увидеть форму функции. Вы можете увидеть прямую линию, изогнутую линию в форме u или n или что-то похожее на волны.

При построении графика перемещайтесь влево или вправо по оси x, в зависимости от того, отрицательна или положительна координата x. Затем вы двигаетесь вверх или вниз по оси y, в зависимости от того, положительна или отрицательна координата y.

После завершения работы проследите за формой графика. Например, если вы нарисуете координаты {(2, 1), (3, 2), (4, 3)}, то они образуют прямую линию, которая идет вверх (1, 2, 3).

2. Найдите минимум функции

Как только вы получите функцию в виде графика, вы сможете увидеть важные особенности, например, минимум. Это самая низкая точка, которую функция достигает визуально. Минимум может быть бесконечным, то есть график неограниченно расширяется вниз. Если это так, то нижний конец диапазона может быть представлен символом бесконечности (?).

3. Найдите максимум функции

Максимум – это наивысшая точка, которую функция достигает визуально. Как и минимум, это число может быть бесконечным. Это также может быть конкретное место на графике, которое можно записать в виде упорядоченной пары. Например, если максимум находится при 3 на оси x и 10 на оси y, то его координаты будут (3, 10).

4. Запишите диапазон в виде эквивалентности

Иногда невозможно написать каждую y-координату функции. Здесь вы можете указать диапазон как эквивалентность, используя символ меньше, чем (<), символ больше чем (>), меньше или равно символу (?) или символ больше или равно (?).

Пример: Для диапазона {-1, 1, 2, 3} вы можете использовать утверждение как:

-1 ? f(x) ? 3

Если ваш диапазон функции имеет бесконечную составляющую, например {-?, 10}, вы можете записать эквивалентность как:

f(x) ? 10

3. Нахождение диапазона функции с помощью отношения

Третий способ найти диапазон функции – записать ее в виде отношения. Отношение – это набор упорядоченных пар, представляющих координаты на графике. Вы можете записать пары отношения в форме (x, y). Ниже описаны шаги, которые можно использовать для нахождения диапазона функции, записанной в виде отношения:

1. Напишите отношение

Когда вы видите набор упорядоченных пар (x, y), вам может быть проще работать с отношением после того, как вы запишете пары на бумаге. Запишите весь набор в фигурных скобках. Например:

{(2, 1), (4, 5), (9, 21) (7, 14), (5, 14)}

2. Составьте список y-координат отношения

Вы можете перечислить y-координаты отношения, взяв второе число из каждой пары координат и записав их в фигурных скобках. Это поможет вам легче представить диапазон значений y.

Это также поможет вам сократить объем информации, с которой вы работаете при нахождении диапазона, или y. Используя приведенный выше пример, вы бы записали y-координаты как:

{1, 5, 21, 14, 14}

3. Удалите все дублирующиеся числа

В этом наборе отношений число 14 встречается дважды. Для нахождения диапазона функции второе 14 не имеет значения, поэтому его можно убрать. Вы можете записать новый список y-координат в виде:

{1, 5, 21, 14}

4. Напишите диапазон от наименьшего до наибольшего

Поскольку числа расположены не по порядку, трудно определить диапазон. Вы можете изменить порядок чисел, чтобы облегчить определение диапазона. Упорядоченный от наименьшего к наибольшему, набор y-координат отношения является таковым:

{1, 5, 14, 21}

Как только вы измените порядок чисел, вы получите диапазон функции с помощью отношения. Итак, для набора отношений:

{(2, 1), (4, 5), (9, 21) (7, 14), (5, 14)}

Диапазон после вычитания:

{1, 5, 14, 21}

5. Убедитесь, что отношение является функцией

Проверив, что каждое значение x дает одно и то же число y, вы можете подтвердить, что отношение является функцией. Отношение является функцией, только если каждому значению x соответствует только одно значение y.

Пример: Если вы вводите x как 2 и получаете на выходе 4, но в следующий раз, когда вы вводите x как 2, вы получаете на выходе 7, то это отношение не является функцией. Если вы каждый раз получаете одно и то же число, то отношение является функцией.

Для примера набора отношений {(2, 1), (4, 5), (9, 21) (7, 14), (5, 14)}, значения x 2, 4, 9, 7 и 5 имеют только одно связанное выходное число каждое, и поэтому это функция, а найденный диапазон функции проверяется.

You have two different ways to define range in math. If you’re doing statistics, the “range” usually means the difference between the highest value and lowest value in a set of data. If you’re doing algebra or calculus, the “range of a set of data” is understood to be the upper and lower bound for a set of possible results, or output values, of a function.

Range in Statistics

If you’re asked to find the range in statistics, you’re simply being asked to find the largest number and smallest number in your data set, and then find the difference between them. Any time you hear “difference,” it’s a clue that you’re about to subtract. The range formula is as follows:

text{highest value} – text{ lowest value} = text{ range}

Range Example 1

Imagine that you snuck a peek at your teacher’s notebook, and you saw that so far, the students’ grade percentages in class are {95, 87, 62, 72, 98, 91, 66, 75}. Curly brackets are often used to enclose a set of numbers, so you know everything inside the curly brackets belongs together.

What’s the range of this data set or, to put it another way, the range of the students’ grades? First, identify the highest data point (98) and the lowest data point (62). Next, subtract the smallest value from the largest value:

98 – 62 = 36

So the range of this particular data set is 36 percentage points.

The Range of a Function

When you begin studying functions in mathematics, you’ll run into a second definition of range. To understand range, it helps to think of functions as little math machines. The set of values you can put into the math machine are called the domain (another very important concept). The set of possible results, once you crank those values through the math machine, is called the ‌codomain‌ And the set of actual results or outputs you get is called the ‌range‌.

There are a couple of important relationships between range and domain that you need to understand. First, within domain and ranges of real number, each value in the domain corresponds to only one value in the range of your function. If any value(s) in the domain correspond to more than one value in the range, you might have a relationship between the two sets of data, but it’s not technically classified as a classical function. However, it is possible for more than one domain value to correspond to the same value in that function’s range.

One of the best ways to make sense of this is to imagine your very own math class. The students in the class represent the domain (or the information that goes into the function), while the class itself is the function or “math machine.” Your final grades represent the range, or what you get after cranking the elements of the domain (students) through the function (math class).

When you look at that example, you can intuitively see that each student is going to receive only one final grade once class is over. Each value in the domain corresponds to only one value in the range. However, it is possible for more than one student to get the same grade. For example, there might be two or three students in your class that studied very hard and managed to get a 96 percent as their final grade. Multiple values in the domain can correspond to a single value in the range.

Range Example 2

Imagine that you’re dealing with the function x^2, with a domain restricted to { −3, −2, −1, 1, 2, 3, 4}. What’s the range of this function?

Although you’ll learn more advanced ways of finding the range later on, for now, the simplest way to find the range of this function is to apply the function to each element of the domain, and track your results. In other words, insert each element of the domain, one at a time, a x in the function x^2. This gives you a set of results:

{9, 4, 1, 1, 4, 9, 16}

But as you can see, some elements are repeated there. Recalling the example of math grades as a function, that’s okay; more than one student can end up with the same grade, or more than one element of the domain can “point” to the same element in the range. But you don’t want to write down the repeated elements when you give the range. So, your answer is simply:

{1, 4, 9, 16}

Notice how the positive numbers and negative numbers in the domain play different roles in the range (in terms of which domain values correspond to the highest numbers and lowest numbers). These relationships are often unique to a function.

What do we use range for?

Descriptive statistics can use many metrics to describe data, and range is very useful for putting these other measurements in context. Arithmetic means and medians are considered measures of central tendency (or what value a set of data can be ‘found around’). Standard deviation and interquartile range are also useful to indicate the distribution of the data around these means and medians, but range provides additional crucial information about the overall spread of data and possible influences from outlying data.

Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.

Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств.  В заключение будет рассмотрена таблица промежутков.

Виды числовых промежутков

Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.

Произведем описание числовых промежутков с выше указанными сторонами:

Этот промежуток имеет соответствующие неравенства x<a или x>a, где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a – (x<a) или больше a – (x>a).

Множество чисел, которые будут удовлетворять неравенству вида x<a обозначается  виде промежутка (−∞, a), а для x>a, как (a, +∞).

Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой  и ее числами имеется соответствие, благодаря которому прямую называем координатной.  Если необходимо сравнить числа, то на координатной прямой большее число находится правее.  Тогда неравенство вида x<a включает в себя точки, которые расположены левее, а для x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.

Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a. Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.

Рассмотрим несколько примеров.

При заданном строгом неравенстве x>−3 задается открытый луч. Эту запись можно представить в виде координат (−3, ∞) . То есть это все точки, лежащие правее, чем -3.

Его задание идет с помощью нестрогих неравенств вида x≤a или x≥a. Для такого вида приняты специальные обозначения вида (−∞, a] и [a, +∞), причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.

Для наглядного примера зададим числовой луч.

Рассмотрим рисунок, приведенный ниже.

Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2≤x≤3, которое изображаем  в виде 2, 3. На координатной прямой данный точки будут включены в решение и закрашены.

Если имеется полуинтервал (1, 3], тогда его обозначение можно в виде двойного неравенства 1<x≤3, при чем на координатной прямой изобразится с точками 1 и 3, где 1 будет исключена, то есть выколота на прямой.

Таблица числовых промежутков

Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.

У вас есть два разных способа определения диапазона в математике. Если вы ведете статистику, «диапазон» обычно означает разницу между самым высоким и самым низким значениями в наборе данных. Если вы выполняете алгебру или исчисление, под «диапазоном» понимается набор возможных результатов или выходных значений функции.

Диапазон в статистике

Если вас попросят найти диапазон в статистике, вас просто попросят найти самое высокое и самое низкое значения в вашем наборе данных, а затем найти разницу между ними. Каждый раз, когда вы слышите «разницу», это ключ, который вы собираетесь вычесть, поэтому формула, которую вы будете использовать:

самое высокое значение – самое низкое значение = диапазон

подсказки

• Не забудьте указать любые единицы измерения (футы, дюймы, фунты, галлоны и т. Д.), Которые могут быть добавлены в ваш набор данных.

Пример 1. Представьте, что вы заглянули в тетрадь своего учителя и увидели, что процентные доли учащихся в классе составляют {95, 87, 62, 72, 98, 91, 66, 75}. Фигурные скобки часто используются для включения набора данных, поэтому вы знаете, что все в фигурных скобках принадлежит друг другу.

Каков диапазон этого набора данных или, другими словами, диапазон оценок учеников? Сначала определите самую высокую точку данных (98) и самую низкую точку данных (62). Затем вычтите самое низкое значение из наибольшего значения:

98 – 62 = 36

Таким образом, диапазон этого конкретного набора данных составляет 36 процентных пунктов.

Диапазон функции

Когда вы начнете изучать функции в математике, вы столкнетесь со вторым определением диапазона. Чтобы понять диапазон, нужно думать о функциях как о маленьких математических машинах. Набор значений, которые вы можете поместить в математическую машину, называется доменом (еще одна очень важная концепция). Набор возможных результатов, как только вы проверяете эти значения с помощью математической машины, называется кодоменом. И набор фактических результатов или результатов, которые вы получаете, называется диапазоном.

Есть несколько важных отношений между диапазоном и областью, которые вам необходимо понять. Во-первых, каждое значение в домене соответствует только одному значению в диапазоне вашей функции. Если какие-либо значения в домене соответствуют более чем одному значению в диапазоне, у вас может быть связь между двумя наборами данных, но технически это не классифицируется как функция. Однако более одного значения домена могут соответствовать одному значению в диапазоне этой функции.

Один из лучших способов понять это – представить свой собственный математический класс. Учащиеся в классе представляют область (или информацию, которая входит в функцию), в то время как сам класс является функцией или «математической машиной». Ваши итоговые оценки представляют диапазон, или то, что вы получаете после запуска элементов домена (учащиеся) с помощью функции (урок математики).

Если вы посмотрите на этот пример, то сможете интуитивно увидеть, что каждый ученик получит только один итоговый балл после окончания урока. Каждое значение в домене соответствует только одному значению в диапазоне. Однако более одного студента могут получить одинаковые оценки. Например, в вашем классе может быть два или три ученика, которые очень усердно учились и сумели набрать 96 процентов в качестве итоговой оценки. Несколько значений в домене могут соответствовать одному значению в диапазоне.

Пример 2. Представьте, что вы имеете дело с функцией x ², с доменом, ограниченным {-3, -2, -1, 1, 2, 3, 4}. Каков диапазон этой функции?

Хотя вы узнаете более продвинутые способы нахождения диапазона позже, на данный момент самый простой способ найти диапазон этой функции – применить функцию к каждому элементу домена и отслеживать ваши результаты. Другими словами, вставьте каждый элемент домена, по одному, как x в функцию x ². Это дает вам набор результатов:

{9, 4, 1, 1, 4, 9, 16}

Но, как видите, некоторые элементы там повторяются. Вспоминая пример математических оценок как функции, ничего страшного; более одного ученика могут получить одинаковую оценку, или более одного элемента домена могут «указывать» на один и тот же элемент в диапазоне. Но вы не хотите записывать повторяющиеся элементы, когда задаете диапазон. Итак, ваш ответ просто:

{1, 4, 9, 16}

Метод интервалов: решение простейших строгих неравенств

12 ноября 2017

• Домашнее задание
• Ответы

Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:

(x − 5)(x + 3) > 0

Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:

Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:

x² − 2x − 15 > 0

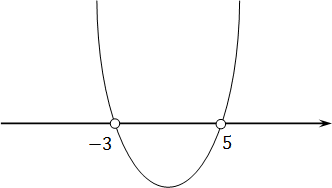
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:

Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.

Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.

Почему эти методы неэффективны?

Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.

Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:

(x − 7)(x − 1)(x + 4)(x + 9) < 0

Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.

Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.

Что такое метод интервалов

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:

1. Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
2. Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
3. Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
4. Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.

Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.

На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:

Задача. Решите неравенство:

(x − 2)(x + 7) < 0

Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:

(x − 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.

Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:

Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:

f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;

Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.

Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.

Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:

Вернемся к исходному неравенству, которое имело вид:

(x − 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

Задача. Решите неравенство:

(x + 9)(x − 3)(1 − x) < 0

Шаг 1: приравниваем левую часть к нулю:

(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.

Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.

Шаг 2: отмечаем все корни на координатной прямой:

Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:

f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.

Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:

Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:

(x + 9)(x − 3)(1 − x) < 0

Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:

x ∈ (−9; 1) ∪ (3; +∞)

Это и есть ответ.

Замечание по поводу знаков функции

Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.

Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:

1. Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
2. Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.

Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.

Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.

Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:

(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;

Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.

Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:

Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.

«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.

На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:

f (x) = (x − 1)(2 + x)(7 − x)

Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.

Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.

Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:

(+) · (+) · (−) = (−)

Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:

Исходное неравенство имело вид:

(x − 1)(2 + x)(7 − x) < 0

Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:

x ∈ (−2; 1) ∪ (7; +∞)

Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:

Задача. Решите неравенство:

x(2x + 8)(x − 3) > 0

Заменяем неравенство уравнением и решаем его:

x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.

Отмечаем все три корня на координатной прямой (сразу со знаками):

Справа на координатной оси стоит плюс, т.к. функция имеет вид:

f (x) = x(2x + 8)(x − 3)

А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:

x ∈ (−4; 0) ∪ (3; +∞)

Смотрите также:

1. Метод интервалов: случай нестрогих неравенств
2. Тест по методу интервалов для строгих неравенств
3. Сводный тест по задачам B12 (2 вариант)
4. Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
5. Формулы приведения: ускоряем вычисления в тригонометрии
6. Задачи B4: перевозка груза тремя фирмами