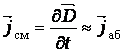Как найти диэлектрическую проницаемость через силу - Сайт, где вы сможете решить свои вопросы

Диэлектрическая проницаемость

Вернутся в раздел ⇒ Законы электротехники коротко

Диэлектрическая проницаемость — величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле:

D = εF
В большинстве диэлектриков при не очень сильных полях диэлектрическая проницаемость не зависит от поля Е. В сильных же электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках в обычных полях зависимость D от Е — нелинейная.

Так же диэлектрическая проницаемость показывает, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия F_o в вакууме:

Относительная диэлектрическая проницаемость вещества может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (C_x) и ёмкости того же конденсатора в вакууме (C_o):

Таблица значений диэлектрической проницаемости для твердых тел:

Таблица значений диэлектрической проницаемости для жидкостей:

Таблица значений диэлектрической проницаемости для газов:

Обозначение в формуле:

D — электрическая индукция в среде;

ε — диэлектрическая проницаемость среды;

E — напряжённость электрического поля;

F₀ — сила взаимодействия между зарядами в среде;

F — сила взаимодействия между зарядами в вакууме;

C_x — ёмкость конденсатора в среде;

C₀ — ёмкость конденсатора в вакууме.

Ещё картинки на тему диэлектрическая проницаемость:

Источник

Содержание

Диэлектрическая проницаемость и электрическая постоянная
Электрическая постоянная
Диэлектрическая проницаемость вещества
Диэлектрическая проницаемость некоторых веществ
Относительная диэлектрическая проницаемость
Содержание
Измерение
Зависимость от частоты
Примечания
См. также
Значения диэлектрической проницаемости для некоторых веществ
Смотреть что такое «Относительная диэлектрическая проницаемость» в других словарях:
Диэлектрическая проницаемость
Диэлектрическая проницаемость

Диэлектрическая проницаемость и электрическая постоянная

Электрическая постоянная — характеристика вакуума, она описывает его электрические свойства. А диэлектрическая проницаемость описывает свойства веществ – диэлектриков, ослабляющих взаимодействие зарядов.

Электрическая постоянная

Обозначают ее (large varepsilon_<0>), она описывает электрические свойства вакуума и является одной из фундаментальных физических постоянных.

Значение электрической постоянной равно:

Совместно с магнитной постоянной (ссылка) (large mu_<0>) определяет скорость, с которой в вакууме распространяются электромагнитные волны (например, видимый свет).

В формуле закона Кулона присутствует константа «k». Число «k» вычисляют по формуле, которая связывает его с постоянной (large varepsilon_<0>) так:

Так же, эта константа встречается в формуле, описывающей напряженность электрического поля.

Диэлектрическая проницаемость вещества

Некоторые вещества могут ослаблять взаимодействие зарядов.

Вещества, ослабляющие взаимодействие заряженных частиц, называют изолирующими веществами, или диэлектриками.

Для пояснения рассмотрим электрические свойства дистиллированной воды.

Расположим в вакууме два положительных заряда на некотором расстоянии один от другого, они будут отталкиваться Кулоновскими силами.

Затем, не меняя заряды и расстояние между ними, переместим их в дистиллированную воду. Мы обнаружим, что в воде они будут отталкиваться слабее в 81 раз (рис. 1).

В нижней части рисунка силы отталкивания зарядов в воде обозначены короткими синими векторами. Длина этих векторов должна быть в 81 раз меньше, чем длина векторов сил в вакууме в верхней части рисунка. Однако, векторы имеют большую длину на рисунке, чем в реальности, так как, если их уменьшить в нужное число раз, то их невозможно будет рассмотреть.

Диэлектрическая проницаемость (large varepsilon) описывает изолирующие свойства диэлектриков. Она показывает, во сколько раз внутри вещества — диэлектрика ослабляется взаимодействие зарядов.

Ослабление взаимодействия происходит за счет ослабления напряженности электростатического поля в диэлектрике.

Диэлектрическая проницаемость некоторых веществ

Вы можете использовать данные таблички для решения большинства школьных задач физики.

Для некоторых веществ значения проницаемости округлены. К примеру, существуют стекла, имеющие значение проницаемости 6,0, и в то же время, проницаемость некоторых стекол может достигать значения 10,0. А в таблице для стекла указано среднее значение 8,0.

Чтобы осуществить более серьезные расчеты, не относящиеся к учебным, пожалуйста, воспользуйтесь специализированными справочниками.

Источник

Относительная диэлектрическая проницаемость

Относи́тельная диэлектри́ческая проница́емость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Относительная диэлектрическая проницаемость воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постоянная воды в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим диполем. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч.

Содержание

Измерение

Относительная диэлектрическая проницаемость вещества ε_r может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (C_x) и ёмкости того же конденсатора в вакууме (C_o):

$varepsilon_<r></noscript>= frac<C_<x>> <C_<0>>.» width=»» height=»»/></p><h2>Практическое применение</h2><p>Диэлектрическая проницаемость диэлектриков является одним из основных параметров при разработке электрических конденсаторов. Использование материалов с высокой диэлектрической проницаемостью позволяют существенно снизить физические размеры конденсаторов.</p><p>Ёмкость конденсаторов определяется:</p><p> <img decoding=$

где ε_r — диэлектрическая проницаемость вещества между обкладками, ε_о — электрическая постоянная, S — площадь обкладок конденсатора, d — расстояние между обкладками.

Параметр диэлектрической проницаемости учитывается при разработке печатных плат. Значение диэлектрической проницаемости вещества между слоями в сочетании с его толщиной влияет на величину естественной статической ёмкости слоев питания, а также существенно влияет на волновое сопротивление проводников на плате.

Зависимость от частоты

Следует отметить, что диэлектрическая проницаемость в значительной степени зависит от частоты электромагнитного поля. Это следует всегда учитывать, поскольку таблицы справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц без указания данного факта. В то же время существуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров. Полученное оптическим методом (частота 10 14 Гц) значение будет значительно отличаться от данных в таблицах.

Рассмотрим, например, случай воды. В случае статического поля (частота равна нулю), относительная диэлектрическая проницаемость при нормальных условиях приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц ε_r начинает падать. В оптическом диапазоне ε_r составляет приблизительно 1,8. Это вполне соответствует факту, что в оптическом диапазоне показатель преломления воды равен 1,33. [1] В узком диапазоне частот, называемом оптическим, диэлектрическое поглощение падает до нуля, что собственно и обеспечивает человеку механизм зрения [источник не указан 665 дней] в земной атмосфере, насыщенной водяным паром. С дальнейшим ростом частоты свойства среды вновь меняются. О поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 10 12 (инфракрасная область) можно прочитать на [1] (англ.)

Примечания

↑ Справочник по элементарной физике. Кошкин Н. И., Ширкевич М. Г. М.: Наука, 1972. — 256с.

См. также

Абсолютная диэлектрическая проницаемость
Диэлектрическая проницаемость вакуума (электрическая константа)
Диэлектрическая восприимчивость
Поляризация диэлектриков

Значения диэлектрической проницаемости для некоторых веществ

Вещество	Химическая формула	Условия измерения	Характерное значение ε_r
Алюминий	Al	1 кГц	-1300 + 1,3·10 14 i
Серебро	Ag	1 кГц	-85 + 8·10 12 i
Вакуум	—	—	1
Воздух	—	Нормальные условия, 0,9 МГц	1,00058986 ± 0,00000050
Углекислый газ	CO₂	Нормальные условия	1,0009
Тефлон	—	—	2,1
Нейлон	—	—	3,2
Полиэтилен	[-СН₂-СН₂-]_n	—	2,25
Полистирол	[-СН₂-С(С₆Н₅)Н-]_n	—	2,4-2,7
Каучук	—	—	2,4
Битум	—	—	2,5-3,0
Сероуглерод	CS₂	—	2,6
Парафин	С₁₈Н₃₈ − С₃₅Н₇₂	—	2,0-3,0
Бумага	—	—	2,0-3,5
Электроактивные полимеры	−	−	2-12
Эбонит	(C₆H₉S)₂	−	2,5-3,0
Плексиглас (оргстекло)	—	—	3,5
Кварц	SiO₂	—	3,5-4,5
Диоксид кремния	SiO₂	−	3,9
Бакелит	—	—	4,5
Бетон	−	−	4,5
Фарфор	−	−	4,5-4,7
Стекло	−	−	4,7 (3,7-10)
Стеклотекстолит FR-4	—	—	4,5-5,2
Гетинакс	—	—	5-6
Слюда	—	—	7,5
Резина	−	−	7
Поликор	98 % Al₂O₃	—	9,7
Алмаз	−	−	5,5-10
Поваренная соль	NaCl	−	3-15
Графит	C	−	10-15
Керамика	−	−	10-20
Кремний	Si	−	11.68
Бор	B	−	2.01
Аммиак	NH₃	20 °C	17
0 °C	20
−40 °C	22
−80 °C	26
Спирт этиловый	C₂H₅OH или CH₃-CH₂-OH	−	27
Метанол	CH₃OH	−	30
Этиленгликоль	HO—CH₂—CH₂—OH	−	37
Фурфурол	C₅H₄O₂	−	42
Глицерин	HOCH₂CH(OH)-CH₂OH или C₃H₅(OH)₃	0 °C	41,2
20 °C	47
25 °C	42,5
Вода	H₂O	200 °C	34,5
100 °C	55,3
20 °C	81
0 °C	88
Плавиковая кислота	HF	0 °C	83,6
Формамид	HCONH₂	20 °C	84
Серная кислота	H₂SO₄	20-25 °C	84-100
Перекись водорода	H₂O₂	−30 °C — +25 °C	128
Синильная кислота	HCN	(0-21 °C)	158
Двуокись титана	TiO₂	—	86-173
Титанат кальция	CaTiO₃	—	170
Титанат стронция	SrTiO₃	—	310
Барий-стронций титанат	—	—	500
Титанат бария	BaTiO₃	(20-120 °C)	1250-10000
Цирконат-титанат свинца	(Pb[Zr_xTi_1-x]O₃, 0 Ссылки

Диэлектрическая проницаемость для различных материалов. В частности, для воздуха — 1,00025
Характеристики FR-4 на 3—4 ГГц и проблема расчёта импеданса проводников с учётом процесса изготовления печатной платы

Wikimedia Foundation . 2010 .

Смотреть что такое «Относительная диэлектрическая проницаемость» в других словарях:

относительная диэлектрическая проницаемость — диэлектрическая проницаемость; относительная диэлектрическая проницаемость; отрасл. диэлектрическая постоянная; диэлектрический коэффициент Отношение абсолютной диэлектрической проницаемости в рассматриваемой точке диэлектрика к электрической… … Политехнический терминологический толковый словарь

относительная диэлектрическая проницаемость — Величина, равная отношению диэлектрической проницаемости вещества к электрической постоянной. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия … Справочник технического переводчика

Относительная диэлектрическая проницаемость — 34. Относительная диэлектрическая проницаемость По ГОСТ 19880 74 Источник: ГОСТ 21515 76: Материалы диэлектрические. Термины и определения оригинал … Словарь-справочник терминов нормативно-технической документации

относительная диэлектрическая проницаемость — santykinė dielektrinė skvarba statusas T sritis chemija apibrėžtis Dydis, rodantis kiek kartų plokščiojo kondensatoriaus su tiriamąja medžiaga talpa yra didesnė už jo talpą, kai tarp kondensatoriaus plokštelių yra vakuumas. atitikmenys: angl.… … Chemijos terminų aiškinamasis žodynas

относительная диэлектрическая проницаемость — santykinė dielektrinė skvarba statusas T sritis automatika atitikmenys: angl. relative dielectric constant; relative permittivity vok. relative Dielektrizitätskonstante, f rus. относительная диэлектрическая проницаемость, f pranc. permittivité… … Automatikos terminų žodynas

относительная диэлектрическая проницаемость — santykinė dielektrinė skvarba statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. relative dielectric constant; relative permittivity vok. relative Permittivität, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

относительная диэлектрическая проницаемость — santykinė dielektrinė skvarba statusas T sritis fizika atitikmenys: angl. relative dielectric constant; relative permittivity vok. Dielektrizitätszahl, f; Elektrisierungszahl, f; relative Dielektrizitätskonstante, f rus. относительная… … Fizikos terminų žodynas

Относительная диэлектрическая проницаемость — 1. Величина, равная отношению диэлектрической проницаемости вещества к электрической постоянной Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий … Телекоммуникационный словарь

Относительная диэлектрическая проницаемость систем вода — органическое вещество — Вода 1,4 диоксан (25 °С) Вода метанол (20 °С) Вода этилендиамин (25 °С) Вода анилин (25 °С) Х2 ε ε∞ … Химический справочник

начальная относительная диэлектрическая проницаемость — Относительная диэлектрическая проницаемость при амплитуде напряженности электрического поля, стремящейся к нулю. [ГОСТ 21515 76] Тематики материалы диэлектрические … Справочник технического переводчика

Источник

Диэлектрическая проницаемость

Лекция №19

Диэлектрическая проницаемость
Природа электропроводности газообразных, жидких и твердых диэлектриков

Диэлектрическая проницаемость

Относительная диэлектрическая проницаемость, или диэлектрическая проницаемость ε— один из важнейших макроскопических электрических параметров диэлектрика. Диэлектрическая проницаемостьε количественно характеризует способность диэлектрика поляризоваться в электрическом поле, а также оценивает степень его полярности; ε является константой диэлектрического материала при данной температуре и частоте электрического напряжения и показывает, во сколько раз заряд конденсатора с диэлектриком больше заряда конденсатора тех же размеров с вакуумом.

Диэлектрическая проницаемость определяет величину электрической емкости изделия (конденсатора, изоляции кабеля и т.п.). Для плоского конденсатора электрическая емкость С, Ф, выражается формулой (1)

где S— площадь измерительного электрода, м 2 ; h — толщина диэлектрика, м. Из формулы (1) видно, что чем больше величина ε используемого диэлектрика, тем больше электрическая емкость конденсатора при тех же габаритах. В свою очередь, электрическая емкость С является коэффициентом пропорциональности между поверхностным зарядом QК, накопленным конденсатором, и приложенным к нему электрическим на-

пряжением U (2):

Из формулы (2) следует, что электрический заряд QК, накопленный конденсатором, пропорционален величине ε диэлектрика. Зная QК игеометрические размеры конденсатора, можно определить ε диэлектрического материала для данного напряжения.

Рассмотрим механизм образования заряда QК на электродах конденсатора с диэлектриком и из каких составляющих складывается этот заряд. Для этого возьмем два плоских конденсатора одинаковых геометрических размеров: один — с вакуумом, другой — с межэлектродным пространством, заполненным диэлектриком, и подадим на них одинаковое электрическое напряжение U (рис. 1). На электродах первого конденсатора образуется заряд Q0, на электродах второго — QК. В свою очередь, заряд QК является суммой зарядов Q0 и Q (3):

Заряд Q0 образован внешним полем Е0 путем накопления на электродах конденсатора сторонних зарядов с поверхностной плотностью σ. Q — это дополнительный заряд на электродах конденсатора, создаваемый источником электрического напряжения для компенсации связанных зарядов, образовавшихся на поверхности диэлектрика.

В равномерно поляризованном диэлектрике заряд Q соответствует величине поверхностной плотности связанных зарядов σ. Заряд σ образует поле Е_сз, направленное противоположно полю Е_{О .}

Диэлектрическую проницаемость рассматриваемого диэлектрика можно представить как отношение заряда QК конденсатора, заполненного диэлектриком, к заряду Q0 такого же конденсатора с вакуумом (3):

Из формулы (3) следует, что диэлектрическая проницаемость ε — величина безразмерная, и у любого диэлектрика она больше единицы; в случае вакуума ε = 1. Из рассмотренного примера также

видно, что плотность заряда на электродах конденсатора с диэлектриком в ε раз больше плотности заряда на электродах конденсатора с вакуумом, а напряженности при одинаковых напряжениях для обо

их конденсаторов одинаковы и зависят только от величины напряжения U и расстояния между электродами (Е = U /h).

Кроме относительной диэлектрической проницаемости ε различают абсолютную диэлектрическую проницаемость ε_а, Ф/м, (4)

которая не имеет физического смысла и используется в электротехнике.

Относительное изменение диэлектрической проницаемости εr при повышении температуры на 1 К называется температурным коэффициентом диэлектрической проницаемости.

ТКε = 1/ εr d εr/dT К-1 Для воздуха при 20°С ТК εr = -2.10-6К-

Электрическое старение в сегнетоэлектриках выражается в уменьшении εr со временем. Причиной является перегруппировка доменов.

Особенно резкое изменение диэлектрической проницаемости со временем наблюдается при температурах, близких к точке Кюри. Нагревание сегнетоэлектриков до температуры более точки Кюри и последующее охлаждение возвращает εr к прежнему значению. Такое же восстановление диэлектрической проницаемости можно осуществить, воздействуя на сегнетоэлектрик электрическим полем повышенной напряженности.

Для сложных диэлектриков – механической смеси двух компонентов с разным εr в первом приближении : εrх = θ1 · εr1х ·θ· εr2х ,где θ – обьемная концентрация компонентов смеси, εr — относительная диэлектрическая проницаемость компонента смеси.

Поляризация диэлектрика может быть вызвана: механическими нагрузками (пьезополяризация в пьезоэлектриках); нагревом (пирополяризация в пироэлектриках); светом (фотополяризация).

Поляризованное состояние диэлектрика в электрическом поле Е характеризуется электрическим моментом единицы объема, поляризованностью Р, Кл/м2, которая связана с его относительной диэлектрической проницаемостью eг : Р = e0 (eг — 1)Е, где e0 = 8,85∙10-12 Ф/м. Произведение e0∙eг =e, Ф/м, называют абсолютной диэлектрической проницаемостью. В газообразных диэлектриках eг мало отличается от 1,0, в неполярных жидких и твердых достигает 1,5 — 3,0, в полярных имеет большие значения; в ионных кристаллах eг — 5-МО, а в имеющих перовскитовую кристаллическую решетку достигает 200; в сегнетоэлектриках eг — 103 и больше.

В неполярных диэлектриках с ростом температуры eг незначительно уменьшается, в полярных изменения связаны с преобладанием того или иного вида поляризации, в ионных кристаллах увеличивается, в некоторых сегнетоэлектриках при температуре Кюри достигает 104 и больше. Температурные изменения eг характеризуют температурным коэффициентом. Для полярных диэлектриков характерным является уменьшение eг в области частот, где время т на поляризацию соизмеримо с Т/2.

Источник

Диэлектрическая проницаемость

Таблица значений диэлектрической проницаемости для твердых тел:

Таблица значений диэлектрической проницаемости для жидкостей:

Таблица значений диэлектрической проницаемости для газов:

Обозначение в формуле:

D — электрическая индукция в среде;

ε — диэлектрическая проницаемость среды;

E — напряжённость электрического поля;

F — сила взаимодействия между зарядами в среде;

F — сила взаимодействия между зарядами в вакууме;

C_x — ёмкость конденсатора в среде;

C — ёмкость конденсатора в вакууме.

Ещё картинки на тему диэлектрическая проницаемость:

Источник

Диэлектрическая проницаемость вещества. Из опытов следует, что взаимодействие электрически заряженных тел в воздухе практически не отличается от их взаимодействия в вакууме. Если заряженные тела находятся в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил их взаимодействия оказывается меньше, чем в вакууме. Чтобы учесть влияние среды, ввели её специальную характеристику, называемую диэлектрической проницаемостью.

Диэлектрическая проницаемость вещества — физическая величина, показывающая, во сколько раз модуль сил электростатического взаимодействия зарядов в данной однородной среде меньше модуля сил взаимодействия этих же зарядов в вакууме:

(17.2)

где F₀ и F — модули сил электростатического взаимодействия зарядов в вакууме и в однородной среде соответственно.

С учётом соотношения (17.2) закон Кулона можно записать следующим образом:

$F equals k fraction numerator open vertical bar q subscript 1 close vertical bar times open vertical bar q subscript 2 close vertical bar over denominator straight epsilon r squared end fraction.$

Диэлектрическая проницаемость вакуума равна 1. За 1 принимают и диэлектрическую проницаемость воздуха, поскольку её значение (при нормальном атмосферном давлении) 1,0006. Диэлектрические проницаемости других однородных сред всегда больше единицы. Например, у воды диэлектрическая проницаемость 81, у глицерина — 56, а у керосина — 2.

От теории к практике

Как и во сколько раз отличаются модули сил электростатического взаимодействия двух точечных зарядов, находящихся на одинаковом расстоянии друг от друга в воде, керосине и глицерине?

Интересно знать

Диэлектрическая проницаемость дистиллированной воды при температуре 25 °C равна 78,54, а при температуре 0 °C — 88. Обычно без указания температуры диэлектрическую проницаемость воды полагают равной 81.

1. К какому виду взаимодействий относят взаимодействие неподвижных электрических зарядов (заряженных тел)?

2. Заряды каких заряженных тел можно считать точечными?

3. Опишите эксперименты Кулона по исследованию взаимодействия электрических зарядов.

4. Сформулируйте закон Кулона. Каковы условия применимости закона Кулона?

5. Чему равен в СИ коэффициент k? Выразите наименование коэффициента пропорциональности k в законе Кулона в основных единицах СИ.

6. В чём суть принципа суперпозиции для электрического взаимодействия точечных зарядов?

7. Что называют диэлектрической проницаемостью среды?

Источник

Диэлектри́ческая проница́емость ( $varepsilon _{r}$ и ${displaystyle varepsilon _{a}}$ ) — коэффициент, входящий в математическую запись закона Кулона для силы взаимодействия точечных зарядов $q_{1}$ и $q_{2}$ , находящихся в однородной изолирующей (диэлектрической) среде на расстоянии $r_{12}$ друг от друга:

${displaystyle F={frac {1}{4pi varepsilon _{a}}}cdot {frac {|q_{1}q_{2}|}{r_{12}^{2}}},}$

а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля:

${displaystyle mathbf {D} =varepsilon _{a}mathbf {E} }$

в рассматриваемой среде^[1].

Вводятся абсолютная ( ${displaystyle varepsilon _{a}}$ ) и относительная ( $varepsilon _{r}$ r, от лат. relativus [-a, -um] — относительный) проницаемости:

${displaystyle varepsilon _{a}=varepsilon _{0}varepsilon _{r},}$

где $varepsilon _{0}$ — электрическая постоянная^[2].

Cам термин «диэлектрическая проницаемость» применяется и для $varepsilon _{r}$ , и для ${displaystyle varepsilon _{a}}$ ; ради краткости, одну из этих величин (в российской литературе чаще $varepsilon _{r}$ , в англоязычной ${displaystyle varepsilon _{a}}$ ) переобозначают как (из контекста обычно ясно, о какой проницаемости идёт речь).

Величина $varepsilon _{r}$ безразмерна, а ${displaystyle varepsilon _{a}}$ по размерности совпадает с $varepsilon _{0}$ (в Международной системе единиц (СИ): фарад на метр, Ф/м).

Проницаемость $varepsilon _{r}$ показывает, во сколько раз сила взаимодействия двух электрических зарядов в конкретной среде меньше, чем в вакууме, для которого ${displaystyle varepsilon _{r}=1}$ .

Отличие проницаемости от единицы обусловлено эффектом поляризации диэлектрика под действием внешнего электрического поля, в результате которой создаётся внутреннее противоположно направленное поле. В области низких частот omega значение проницаемости реальных сред ${displaystyle varepsilon _{r}>1}$ , обычно оно лежит в диапазоне 1—100, но для сегнетоэлектриков составляет десятки и сотни тысяч. Как функция частоты электрического поля величина ${displaystyle varepsilon _{r}(omega )}$ слегка возрастает на участках вне полос или линий поглощения электромагнитного излучения данным материалом, однако вблизи линий или полос резко спадает, из-за чего высокочастотная диэлектрическая проницаемость ниже статической. Имеет место связь проницаемости и показателя преломления вещества: для немагнитной непоглощающей среды ${displaystyle n^{2}(omega )=varepsilon _{r}(omega ).}$

Относительная диэлектрическая проницаемость $varepsilon _{r}$ является одним из «электромагнитных параметров» среды, влияющих на распределение компонент вектора напряжённости электромагнитного поля в пространстве и описывающих среду в материальных уравнениях электродинамики (уравнениях Максвелла).

Абсолютная диэлектрическая проницаемость вакуума[править | править код]

Электрическая постоянная, она же «абсолютная диэлектрическая проницаемость вакуума», в системе единиц СИ равна:

${displaystyle varepsilon _{0}approx 8{,}85cdot 10^{-12}}$

Ф/м

(имеет размерность L⁻³ M⁻¹ T⁴ I²).

В системе СГС эта же постоянная составляет ${displaystyle varepsilon _{0}=1/4pi ,}$ однако часто в СГС вообще не используют $varepsilon _{0}$ , надлежащим образом видоизменяя формулы. Например, закон Кулона:

${displaystyle F=varepsilon _{r}^{-1}cdot |q_{1}q_{2}|/r_{12}^{2}.}$

Электрическая постоянная связана с магнитной постоянной и скоростью света в вакууме:

${displaystyle varepsilon _{0}mu _{0}=c^{-2}.}$

Ниже все формулы приводятся для СИ, а символ используется как замена $varepsilon _{r}$ ( ${displaystyle varepsilon _{a}=varepsilon _{0}varepsilon }$ ).

Эффект поляризации диэлектрика и проницаемость[править | править код]

Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля

Под воздействием электрического поля в диэлектрике происходит поляризация — явление, связанное с ограниченным смещением зарядов относительно положения равновесия без наложенного электрического поля или поворотом электрических диполей.

Это явление характеризует вектор электрической поляризации равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. на рисунке сверху), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (на рисунке снизу), в зависимости от восприимчивости конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость .

Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей материала. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге то, что ${displaystyle varepsilon _{a}neq varepsilon _{0}}$ является следствием электрической поляризации материалов.

Роль диэлектрической проницаемости среды в физике[править | править код]

Относительная диэлектрическая проницаемость среды, наряду с её относительной магнитной проницаемостью и удельной электропроводностью влияет на распределение напряжённости электромагнитного поля в пространстве и используется при описании среды в системе уравнений Максвелла.

Среду со значениями mu =1 и называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды.

Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых ) также влияет на значение тангенса угла диэлектрических потерь и коэффициент поглощения электромагнитной волны в среде.

Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников: увеличение приводит к увеличению ёмкости. При изменении в пространстве (то есть, если зависит от координат) говорят о неоднородной среде, зависимость от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость от напряженности электрического поля — одна из возможных причин нелинейности среды. Если среда является анизотропной, то в материальном уравнении будет не скаляром, а тензором. При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде () оперируют комплексной диэлектрической проницаемостью.

Таким образом, является одним из важнейших «электромагнитных параметров» соответствующей среды.

Диэлектрическая проницаемость непоглощающей среды[править | править код]

Проницаемость и связанные с ней величины[править | править код]

Применительно к диэлектрической среде без потерь справедливы соотношения:

${displaystyle mathbf {D} =varepsilon _{0}mathbf {E} +mathbf {P} =varepsilon _{0}(1+chi )mathbf {E} =varepsilon _{0}varepsilon mathbf {E} .}$

В большинстве случаев chi и, соответственно, — это просто безразмерные константы конкретного материала. В вакууме chi равно нулю.

Особая ситуация возникает для нелинейных сред, когда зависит от величины поля ; такое возможно в сравнительно сильных полях. В сегнетоэлектриках возможно появление спонтанной поляризации, а именно сохранение поляризации после снятия ранее наложенного внешнего поля.

Распределение электрического поля в пространстве с различными диэлектриками находится из численного решения уравнения Максвелла:

{displaystyle {boldsymbol {nabla }}cdot mathbf {D(r)} =rho (mathbf {r} ),}

или уравнения Пуассона для электрического потенциала

${displaystyle {boldsymbol {nabla }}left(varepsilon (mathbf {r} ){boldsymbol {nabla }}varphi (mathbf {r} )right)=-varepsilon _{0}^{-1}rho (mathbf {r} ),}$

где

обозначает плотность свободных зарядов.

На незаряженной границе двух диэлектрических сред отношение нормальных компонент напряжённости поля $E_{n}$ с обеих сторон равно обратному отношению значений проницаемости сред.

В случае однородного диэлектрика его наличие приводит к снижению электрического поля в раз, по сравнению со случаем вакуума при том же распределении свободных зарядов. Помимо закона Кулона, практически важным примером является конденсатор любой геометрии, заряд (но не разность потенциалов) обкладок которого фиксирован.

Проницаемость в оптическом диапазоне частот[править | править код]

Диэлектрическая проницаемость, совместно с магнитной, определяют фазовую скорость распространения электромагнитной волны в рассматриваемой среде, а именно:

${displaystyle varepsilon _{0}varepsilon (omega )mu _{0}mu (omega )=v_{ph}^{-2}.}$

Показатель преломления диэлектрика без потерь можно выразить как квадратный корень из произведения его магнитной и диэлектрической проницаемостей:

{displaystyle n(omega )={sqrt {mu (omega )cdot varepsilon (omega )}}.}

Для немагнитных сред Значения для существенного в конкретном контексте оптического диапазона могут очень сильно отличаться от статических значений: как правило, намного ниже, чем для статического поля.

Однако, если рассматривать оптический диапазон частот сам по себе, то в нём с ростом omega величина (а значит, и ) чаще всего возрастает. Такое поведение показателя преломления («синий свет преломляется сильнее красного») является случаем так называемой нормальной дисперсии. Противоположную ситуацию аномальную дисперсию можно наблюдать вблизи полос поглощения, но такой случай не может рассматриваться как случай без диссипативных потерь.

Тензор проницаемости анизотропных сред[править | править код]

Диэлектрическая проницаемость связывает электрическую индукцию и напряжённость электрического поля

В электрически анизотропных средах компонента вектора напряжённости $E_{i}$ может не только влиять на ту же самую компоненту вектора электрической индукции ${displaystyle D_{i},}$ но и порождать другие его компоненты ${displaystyle D_{j}(jneq i).}$

В общем случае проницаемость является тензором, определяемым из следующего соотношения (в записи использовано соглашение Эйнштейна):

${displaystyle D_{i}=varepsilon _{0}varepsilon _{ij}E_{j},}$

или, иначе:

${displaystyle mathbf {D} ={boldsymbol {varepsilon }}_{a}mathbf {E} ,}$

где жирный шрифт использован для векторных и тензорных величин, а

${displaystyle mathbf {E} =E_{1}mathbf {e} _{1}+E_{2}mathbf {e} _{2}+E_{3}mathbf {e} _{3}}$ — вектор напряжённости электрического поля,

${displaystyle mathbf {D} =D_{1}mathbf {e} _{1}+D_{2}mathbf {e} _{2}+D_{3}mathbf {e} _{3}}$

— вектор электрической индукции,

${displaystyle {boldsymbol {varepsilon }}_{a}=varepsilon _{0}varepsilon _{ij}}$

— тензор абсолютной диэлектрической проницаемости.

В изотропном случае любая компонента вектора напряженности $E_{i}$ влияет только на ${displaystyle D_{i},}$ при этом ${displaystyle varepsilon _{ij}=~delta _{ij}varepsilon ,}$ где ${displaystyle delta _{ij}-}$ символ Кронекера, поэтому уравнения Максвелла могут быть записаны с использованием скалярной диэлектрической проницаемости ( просто коэффициент в уравнении).

Статическая проницаемость некоторых диэлектриков[править | править код]

Значение вакуума равно единице, для реальных сред в статическом поле Для воздуха и большинства других газов в нормальных условиях значение близко к единице в силу их низкой плотности. В статическом электрическом поле для большинства твёрдых или жидких диэлектриков значение лежит в интервале от 2 до 8, для жидкой воды значение достаточно высокое, 88 при ${displaystyle 0^{circ }.}$ А у твердого льда больше и составляет 97 при ${displaystyle 0^{circ }.}$ Это объясняется тем, что переход атома Н от одного атома кислорода к другому атому вызывает перестройку ковалентных и водородных связей у обоих этих атомов кислорода и в их в окрестности. В результате вся структура ковалентных и водородных связей во льду сильно флуктуирует, и это приводит к аномально высокой поляризуемости льда, превосходя диэлектрическую проницаемость жидкой воды^[3].

Значение велико для веществ с молекулами, обладающими большим электрическим дипольным моментом. Значение сегнетоэлектриков составляет десятки и сотни тысяч.

Статическая диэлектрическая проницаемость материалов (таблица)
Вещество	Химическая формула	Условия измерения	Характерное значение ε_r
Вакуум	–	–	1
Воздух	–	Нормальные условия, 0,9 МГц	1,00058986 ± 0,00000050
Углекислый газ		Нормальные условия	1,0009
Тефлон (политетрафторэтилен, фторопласт)	${displaystyle {ce {[{-CF2-CF2-}]_n}}}$	–	2,1
Нейлон	–	–	3,2
Полиэтилен	${displaystyle {ce {[{-CH2-CH2-}]_n}}}$	–	2,25
Полистирол	${displaystyle {ce {[{-CH2-{(C6H5)}H-}]_{n}}}}$	–	2,4-2,7
Каучук	–	–	2,4
Битум	–	–	2,5-3,0
Сероуглерод		–	2,6
Парафин		–	2,0-3,0
Бумага	–	–	2,0-3,5
Электроактивные полимеры	−	−	2-12
Эбонит	${displaystyle {ce {(C6H9S)_2}}}$	−	2,5-3,0
Плексиглас (оргстекло)	–	–	3,5
Кварц		–	3,5-4,5
Диоксид кремния		−	3,9
Бакелит	–	–	4,5
Бетон	−	−	4,5
Фарфор	−	−	4,5-4,7
Стекло	−	−	4,7 (3,7-10)
Стеклотекстолит FR-4	–	–	4,5-5,2
Гетинакс	–	–	5-6
Слюда	–	–	7,5
Резина	−	−	7
Поликор	98 %	–	9,7
Алмаз		Нормальные условия	5,5-10
Поваренная соль		−	3-15
Графит		−	10-15
Керамика	−	−	10-20
Кремний		−	11.68
Бор		−	2.01
Аммиак		20 °C	17
		0 °C	20
		−40 °C	22
		−80 °C	26
Спирт этиловый	или	−	27
Метанол		−	30
Этиленгликоль		−	37
Фурфурол		−	42
Глицерин	или ${displaystyle {ce {C3H5(OH)_3}}}$	0 °C	41,2
		20 °C	47
		25 °C	42,5
Вода		200 °C	34,5
		100 °C	55,3
		20 °C	81
		0 °C	88
Плавиковая кислота		0 °C	83,6
Формамид		20 °C	84
Серная кислота		20-25 °C	84-100
Пероксид водорода		−30 °C — +25 °C	128
Синильная кислота		(0-21 °C)	158
Диоксид титана		–	86-173
Титанат кальция		–	170
Титанат стронция		–	310
Титанат бария-стронция	${displaystyle {ce {(Ba_{1-x}Sr_x)TiO3}}}$ ,	–	500
Титанат бария		(20-120 °C)	1250-10000
Цирконат-титанат свинца	${displaystyle {ce {(Pb[Zr_xTi_{1-x}]O3)}}}$ , )		500-6000
Сополимеры	–	–	до 100000
Сульфид кадмия			9,3

Большой диэлектрической проницаемостью обладают некоторые сложные вещества: CCTO-керамика и LSNO-керамика ( около 10² и 10⁶ соответственно)^[4].

Кроме того, исследуются и метаматериалы. Например диэлектрическая проницаемость порядка 10⁷—10⁸ была обнаружена у металлических наноостровковых структур на диэлектрических подложках^[5]^[6].

В электронике диэлектрическая проницаемость изоляционных материалов является одним из основных параметров для электрических конденсаторов. Применение материала с высокой диэлектрической проницаемостью позволяет существенно сократить габаритные размеры конденсатора. Например, ёмкость плоского конденсатора:

${displaystyle C=varepsilon _{0}varepsilon {frac {S}{d}},}$

где

— относительная диэлектрическая проницаемость материала между обкладками,

— площадь обкладок конденсатора,

— расстояние между обкладками.

Таким образом, требуемая площадь обкладок обратно пропорциональна Значение диэлектрической проницаемости материала основания учитывается при разработке печатных плат, поскольку оно влияет на значение статической ёмкости проводящего рисунка слоёв питания и волновое сопротивление проводников (линий передачи сигналов) на плате.

Помимо обозначения ранее для относительной диэлектрической проницаемости иногда применялось обозначение которое при отсутствии греческих шрифтов заменяли на . Это обозначение ныне почти не используется и сохранилось лишь применительно к диэлектрикам в полевых транзисторах с изолированным затвором.

Традиционно в таких приборах используется диоксид кремния (SiO₂). Однако в целях миниатюризации транзисторов на определённом этапе потребовался переход к материалам с более высокой, чем у SiO₂ (3,9), проницаемостью. Это позволяет получить нужную ёмкость при более толстом^[7] слое материала, что полезно, так как для тонких слоёв актуальны проблемы надёжности и туннельных утечек. Примерами применяемых подзатворных «high-k» диэлектриков являются ZrO₂, HfO₂ (у двух названных материалов ), TiO₂ () и ряд других. Микросхемы на базе транзисторов с такими материалами начали серийно выпускаться в 2000-е годы^[8]. Поиск новых подзатворных материалов продолжается.

Проницаемость диэлектрической среды с потерями[править | править код]

Комплексная диэлектрическая проницаемость[править | править код]

При описании колебаний электрического поля методом комплексных амплитуд в случае диэлектрической среды с конечной проводимостью sigma уравнения Максвелла можно записывать по аналогии со случаем идеального диэлектрика, если ввести мнимую компоненту проницаемости.

Пусть напряженность электрического поля изменяется во времени по гармоническому закону (далее — мнимая единица):

${displaystyle mathbf {E} =mathbf {E} _{0}e^{-iomega t}.}$

Тогда , а уравнение Максвелла для магнитного поля применительно к проводящей среде выглядит:

${displaystyle {boldsymbol {nabla }}times mathbf {H} =mathbf {j} +{frac {partial mathbf {D} }{partial t}}=sigma mathbf {E} +varepsilon _{0}varepsilon {frac {partial mathbf {E} }{partial t}}=varepsilon _{0}left(varepsilon +{frac {isigma }{varepsilon _{0}omega }}right){frac {partial mathbf {E} }{partial t}}.}$

Чтобы привести это уравнение к виду, формально совпадающему с видом уравнения для непроводящей среды, величина, стоящая в скобках, интерпретируется как комплексная диэлектрическая проницаемость Значок сверху (опускаемый, если это не влечёт двусмысленности) подчеркивает, что речь идёт о комплексной величине. При наличии анизотропии становится тензорной величиной. Иногда в методе комплексных амплитуд используют зависимость вида ${displaystyle mathbf {E} =mathbf {E} _{0}e^{iomega t}}$ — тогда знак перед должен быть заменён везде.

Даже в случаях, когда в постоянном электрическом поле среда обладает очень малой проводимостью, на высоких частотах могут проявиться существенные потери, которые при таком подходе приписываются некоторой «эффективной» диэлектрической проницаемости:

{displaystyle {hat {varepsilon }}=varepsilon '+mathrm {i} varepsilon ''.}

Наличие мнимой части связано с конечной проводимостью которая и обусловливает поглощение. Если частота изменения поля составляет omega , то ${displaystyle varepsilon ''=sigma /varepsilon _{0}omega }$ .

Без метода комплексных амплитуд подставлять комплексную в уравнения Максвелла нельзя (следует оперировать непосредственно и sigma ). Однако если известны и то можно воспользоваться ими для анализа свойств среды, вычисления ряда других параметров включая показатель поглощения, а также получить готовыми и ${displaystyle sigma =varepsilon _{0}|varepsilon ''|cdot omega }$ для соответствующей частоты.

Характеристика диэлектрических потерь[править | править код]

Плотность мощности (Ватт/м³) тепловыделения за счёт диэлектрических потерь составляет:

${displaystyle w_{mathrm {loss} }={frac {W_{mathrm {loss} }}{V}}=omega cdot varepsilon _{0}cdot |varepsilon ''|cdot E^{2}.}$

Подобный механизм разогрева широко используется в микроволновых печах. Для характеристики диэлектрика с поглощением также используется величина «тангенса угла потерь» — отношение мнимой и вещественной частей комплексной диэлектрической проницаемости:

${displaystyle {rm {{tg},delta ={frac {|varepsilon ''|}{varepsilon '}}={frac {sigma }{omega varepsilon _{0}varepsilon '}}.}}}$

При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол , где δ — угол диэлектрических потерь.

При отсутствии потерь δ = 0. Тангенс угла потерь определяется отношением активной мощности к реактивной при синусоидальном напряжении заданной частоты. Величина, обратная tg δ, называется добротностью конденсатора.

При наличии поглощения взаимосвязь между компонентами комплексной проницаемости и оптическими величинами (показателями преломления и поглощения) устанавливается с использованием соотношений Крамерса — Кронига и имеет вид:

${displaystyle (n+mathrm {i} k)^{2}=(varepsilon '+mathrm {i} varepsilon '')mu ,}$

откуда для немагнитных сред следует:

${displaystyle n^{2}={frac {1}{2}}cdot left({sqrt {varepsilon '^{2}+varepsilon ^{prime prime 2}}}+varepsilon 'right),}$

${displaystyle k^{2}={frac {1}{2}}cdot left({sqrt {varepsilon '^{2}+varepsilon ^{prime prime 2}}}-varepsilon 'right).}$

Типичная частотная зависимость проницаемости[править | править код]

Типичное поведение вещественной и мнимой составляющих диэлектрической проницаемости в широком диапазоне частот. Области резкого изменения этих составляющих соответствуют линиям поглощения, которые могут иметь различную природу: дипольная или ионная релаксация, атомные и электронные резонансы на высоких частотах^[9]. СВЧ — сверхвысокие частоты, ИК — инфракрасный диапазон, ВД — видимый диапазон, УФ — ультрафиолетовый диапазон.

Зависимость действительной и мнимой составляющих диэлектрической проницаемости воды при 20 °C

Параметры и sigma обычно сильно зависят от частоты колебаний напряженности электрического поля. Например, ясно, что в дипольной модели поляризации процесс ориентации диполей может не успевать следовать за изменениями приложенного поля, что может проявиться как возрастанием, так и снижением проницаемости по сравнению с её статическим значением.

Наиболее типичное поведение и как функций частоты omega представлено на рисунке. Далеко от линий и полос поглощения («собственных частот») материала значения малы, а не изменяется или слабо растёт с частотой. В областях вблизи линий компонента имеет максимумы, а резко спадает. При этом не исключена ситуация, при которой в каком-то диапазоне окажется отрицательным или положительным, но меньше единицы. Практически является редким случаем, а ситуация на предельно высоких (рентгеновских) частотах характерна для всех материалов: в этой области с ростом omega подходит к единице снизу.

Таблицы неспециализированных справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц (иногда даже без указания данного факта). В то же время значения в оптическом диапазоне (частота 10¹⁴ Гц) намного отличаются в меньшую сторону от данных, представленных в подобных таблицах. Например для воды в случае статического поля относительная диэлектрическая проницаемость приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц (здесь ) начинает падать. В оптическом диапазоне составляет около 1,77, соответственно показатель преломления воды равен 1,33, а не квадратному корню из восьмидесяти.

Сведения о поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 10¹² (инфракрасная область) можно найти на сайте (англ.).

Измерение диэлектрической проницаемости[править | править код]

Относительная диэлектрическая проницаемость вещества может быть определена путём сравнения ёмкости тестового конденсатора с данным диэлектриком ( $C_{x}$ ) и ёмкости того же конденсатора в вакууме ( $C_{0}$ ):

${displaystyle varepsilon ={frac {C_{x}}{C_{0}}}.}$

Cуществуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров.

Примечания[править | править код]

↑ Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.
↑ Никольский В. В. , Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989. С. 35.
↑ Финкельштейн А. В. Физика белка / Птицын О. Б.. — 3-е изд. — М.: КДУ, 2012. — С. 45. — 456 с. — ISBN 5-98227-065-2.
↑ Элементы – новости науки: Найдено вещество с гигантским значением диэлектрической проницаемости. elementy.ru. Дата обращения: 11 февраля 2017. Архивировано 11 февраля 2017 года.
↑ Наноструктуры, превосходящие сегнетоэлектрики (рус.). Архивировано 11 февраля 2017 года. Дата обращения: 11 февраля 2017.
↑ Архивированная копия. Дата обращения: 15 февраля 2017. Архивировано 16 февраля 2017 года.
↑ Ёмкость плоского конденсатора ${displaystyle C={frac {varepsilon S}{d}}}$ , где d — расстояние между обкладками. Чем больше d, тем меньше ёмкость. Увеличенная проницаемость может это компенсировать.
↑ High-k Gate Dielectrics / Michel Houssa. — CRC Press, 2004. — 601 p. — (Series in Material Science and Engineering). — ISBN 0750309067.
↑ Dielectric Spectroscopy Архивировано 7 марта 2001 года.

Ссылки[править | править код]

Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1965.
Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
Малышкина И. А. Основы метода диэлектрической спектроскопии (учебное пособие) // Изд-во физического ф-та МГУ, М.: 2012 — 81 стр.
Курс физики для ФМШ при НГУ, раздел «Электромагнитное поле», гл. 2: «Диэлектрики».

Источник

Диэлектри́ческая
проница́емость среды — физическая
величина,
характеризующая свойства изолирующей (диэлектрической)
среды и показывающая зависимостьэлектрической
индукции от напряжённости
электрического поля.

Определяется
эффектом поляризации диэлектриков под
действием электрического поля (и с
характеризующей этот эффект
величиной диэлектрической
восприимчивости среды).

Различают
относительную и абсолютную диэлектрические
проницаемости.

Относительная
диэлектрическая проницаемость ε
является
безразмерной и показывает, во сколько
раз сила взаимодействия двух электрических
зарядов в среде меньше, чем в вакууме.
Эта величина для воздуха и
большинства других газов в нормальных
условиях близка к единице (в силу их
низкой плотности). Для большинства
твёрдых или жидких диэлектриков
относительная диэлектрическая
проницаемость лежит в диапазоне от 2 до
8 (для статического поля). Диэлектрическая
постояннаяводы в
статическом поле достаточно высока —
около 80. Велики её значения для веществ
с молекулами, обладающими большим электрическим
дипольным моментом.
Относительная диэлектрическая
проницаемость сегнетоэлектриков составляет
десятки и сотни тысяч.

Абсолютная
диэлектрическая проницаемость в
зарубежной литературе обозначается
буквой ε,
в отечественной преимущественно
используется сочетание ,
где — электрическая
постоянная.
Абсолютная диэлектрическая проницаемость
используется только в Международной
системе единиц (СИ),
в которой индукция и напряжённость
электрического поля измеряются в
различных единицах. В системе
СГС необходимость
в введении абсолютной диэлектрической
проницаемости отсутствует. Абсолютная
диэлектрическая постоянная (как и
электрическая постоянная) имеет
размерность L⁻³M⁻¹T⁴I².
В единицах Международной
системы единиц (СИ):
[]=Ф/м.

Следует
отметить, что диэлектрическая проницаемость
в значительной степени зависит от
частоты электромагнитного поля. Это
следует всегда учитывать, поскольку
таблицы справочников обычно содержат
данные для статического поля или малых
частот вплоть до нескольких единиц кГц
без указания данного факта. В то же время
существуют и оптические методы получения
относительной диэлектрической
проницаемости по коэффициенту преломления
при помощи эллипсометров и рефрактометров.
Полученное оптическим методом (частота
10¹⁴ Гц)
значение будет значительно отличаться
от данных в таблицах.

Рассмотрим,
например, случай воды. В случае статического
поля (частота равна нулю), относительная
диэлектрическая проницаемость
при нормальных
условияхприблизительно
равна 80. Это имеет место вплоть до
инфракрасных частот. Начиная примерно
с 2 ГГц ε_r начинает
падать. В оптическом диапазоне ε_r составляет
приблизительно 1,8. Это вполне соответствует
факту, что в оптическом диапазоне
показатель преломления воды равен
1,33.^[1] В
узком диапазоне частот, называемом
оптическим, диэлектрическое поглощение
падает до нуля, что собственно и
обеспечивает человеку механизм
зрения^[^{источник не указан 1252 дня}^] в
земной атмосфере, насыщенной водяным
паром. С дальнейшим ростом частоты
свойства среды вновь меняются. О поведении
относительной диэлектрической
проницаемости воды в диапазоне частот
от 0 до 10¹² (инфракрасная
область) можно прочитать на [1] (англ.)

Диэлектрическая
проницаемость диэлектриков является
одним из основных параметров при
разработке электрических
конденсаторов.
Использование материалов с высокой
диэлектрической проницаемостью позволяют
существенно снизить физические размеры
конденсаторов.

Ёмкость
конденсаторов определяется:

где ε_r —
диэлектрическая проницаемость вещества
между обкладками, ε_о — электрическая
постоянная, S —
площадь обкладок конденсатора, d —
расстояние между обкладками.

Параметр
диэлектрической проницаемости учитывается
при разработке печатных
плат.
Значение диэлектрической проницаемости
вещества между слоями в сочетании с его
толщиной влияет на величину естественной
статической ёмкости слоев питания, а
также существенно влияет на волновое
сопротивлениепроводников
на плате.

УДЕЛЬНОЕ
СОПРОТИВЛЕНИЕ электрическое, физическая
величина , равная электрическому
сопротивлению (см.СОПРОТИВЛЕНИЕ
ЭЛЕКТРИЧЕСКОЕ) R
цилиндрического проводника единичной
длины (l = 1м) и единичной площади поперечного
сечения (S =1 м²)..
r
= R S/l.
В
Си единицей удельного сопротивления
является Ом^.м.
Удельное
сопротивление могут выражать также в
Ом^.см.
Удельное
сопротивление является характеристикой
материала, по которому протекает ток,
и зависит от материала, из которого он
изготовлен. Удельное сопротивление,
равное r = 1 Ом^.м
означает, что цилиндрический проводник,
изготовленный из данного материала,
длиной l = 1м и с площадью поперечного
сечения S = 1 м² имеет
сопротивление R = 1 Ом^.м.
Величина
удельного сопротивления металлов (см. МЕТАЛЛЫ),
являющихся хорошими проводниками (см. ПРОВОДНИКИ),
может иметь значения порядка 10^–⁸ –
10^–⁶Ом^.м
(например, медь, серебро, железо и т. д.).
Удельное сопротивление некоторых
твердых диэлектриков (см. ДИЭЛЕКТРИКИ) может
достигать значения 10¹⁶-10¹⁸Ом.м
(например, кварцевое стекло, полиэтилен,
электрофарфор и др.). Величина удельного
сопротивления многих материалов
(особенного полупроводниковых
материалов (см.ПОЛУПРОВОДНИКОВЫЕ
МАТЕРИАЛЫ))
существенно зависит от степени их
очистки, наличия легирующих добавок,
термических и механических обработок
и т. д.

Величина
s, обратная удельному сопротивлению ,
называется удельной проводимостью:
s
= 1/r
Удельная
проводимость измеряется в сименсах (см. СИМЕНС
(единица проводимости)) на
метр См/м.
Удельное
электрическое сопротивление (проводимость)
является скалярной величиной для
изотропного вещества; и тензорной —
для анизотропного вещества.
В
анизотропным монокристаллах анизотропия
электропроводности является следствием
анизотропии обратной эффективной
массы (см. ЭФФЕКТИВНАЯ
МАССА) электронов
и дырок.

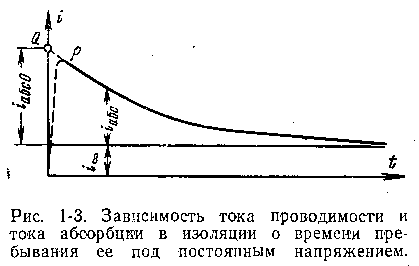
1-6.
ЭЛЕКТРОПРОВОДНОСТЬ ИЗОЛЯЦИИ

При
включении изоляции кабеля или провода
на постоянное напряжение U через нее
проходит ток i, изменяющийся во времени
(рис. 1-3). Этот ток имеет постоянные
составляющие – ток проводимости (i_∞ )
и ток абсорбции,
где γ
– проводимость,
соответствующая току абсорбции; Т –
время, в течение которого ток i_абс спадает
до 1/e своего первоначального значения.
При бесконечно большом времени i_абс →0
и i = i_∞ .
Электропроводность диэлектриков
объясняется наличием в них некоторого
количества свободных заряженных частиц:
ионов и электронов.

Наиболее
характерна для большей части
электроизоляционных материалов ионная
электропроводность, которая возможна
за счет неизбежно присутствующих в
изоляции загрязнений (примеси влаги,
солей, щелочей и т. п.). У диэлектрика с
ионным характером электропроводности
строго соблюдается закон Фарадея –
пропорциональность между количеством
прошедшего через изоляцию электричества
и количеством выделившегося при
электролизе вещества.

При
повышении температуры удельное
сопротивление электроизоляционных
материалов уменьшается и характеризуется
формулой

где_ρ_о ,
А и В – постоянные для данного материала;
Т- температура, °К.

Большая
зависимость сопротивления изоляции от
влаги имеет место у гигроскопичных
изоляционных материалов, главным образом
волокнистых (бумага, хлопчатобумажная
пряжа и др.). Поэтому волокнистые материалы
подвергаются сушке и пропитке, а также
защите влагостойкими оболочками.

Сопротивление
изоляции может уменьшаться с повышением
напряжения за счет образования в
изоляционных материалах объемных
зарядов. Создающаяся при этом добавочная
электронная проводимость приводит к
увеличению электропроводности. Существует
зависимость проводимости от напряжения
в очень сильных полях (закон Я. И.
Френкеля):

где
γ_о –
проводимость в слабых полях; а – постоянная.
Все электроизоляционные материалы
характеризуются определенными значениями
проводимости изоляции G. В идеале
проводимость изоляционных материалов
равна нулю. У реальных изоляционных
материалов проводимость на единицу
длины кабеля определяют по формуле

В
кабелях, имеющих сопротивление изоляции
более , 3-10¹¹ ом-м
и кабелях связи, где потери на
диэлектрическую поляризацию значительно
больше тепловых потерь, проводимость
определяют по формуле

Проводимость
изоляции в технике связи является
электрическим параметром линии,
характеризующим потери энергии в
изоляции жил кабелей. Зависимость
величины проводимости от частоты
приведена на рис. 1-1. Величина, обратная
проводимости – сопротивление изоляции,
представляет собой отношение приложенного
к изоляции
напряжения постоянного тока (в вольтах)
к току
утечки (в амперах), т. е.

где R_V –
объемное сопротивление изоляции,
численно определяющее препятствие,
создаваемое прохождению тока в
толще изоляции; R_S –
поверхностное сопротивление, определяющее
препятствие прохождению тока по
поверхности изоляции.

Практической
оценкой качества применяемых изоляционных
материалов является удельное объемное
сопротивление ρ_V выражаемое
в омо-сантиметрах (ом*см). Численно
ρ_V равно
сопротивлению (в омах) куба с ребром 1
см из данного материала, если ток проходит
через две противоположные грани куба.
Удельное поверхностное сопротивление
ρ_S численно
равно сопротивлению поверхности квадрата
(в омах), если ток подводится к электродам,
ограничивающим две противоположные
стороны этого квадрата.

Сопротивление
изоляции одножильного кабеля или провода
определяют по формуле

Абсорбционными
токами называются токи смещения различных
видов замедленной поляризации.
Абсорбционные токи при постоянном
напряжении протекают в диэлектрике до
момента установления равновесного
состояния, изменяя свое направление
при включении и выключении напряжения.
При переменном напряжении абсорбционные
токи протекают в течение всего времени
нахождения диэлектрика в электрическом
поле.

Влажностные
свойства диэлектриков

Влагостойкость
– это
надежность эксплуатации изоляции при
нахождении ее в атмосфере водяного пара
близкого к насыщению. Влагостойкость
оценивают по изменению электрических,
механических и других физических свойств
после нахождения материала в атмосфере
с повышенной и высокой влажностью;
по влаго- и водопроницаемости;
по влаго- и водопоглощаемости.

Влагопроницаемость
– способность
материала пропускать пары влаги при
наличии разности относительных влажностей
воздуха с двух сторон материала.

Влагопоглощаемость – способность
материала сорбировать воду при
длительном нахождении во влажной
атмосфере близкой к состоянию насыщения.

Водопоглощаемость – способность
материала сорбировать воду при
длительном погружении его в воду.

Тропикостойкость и тропикализация оборудования – защита
электрооборудования от влаги, плесени,
грызунов.

Тепловые
свойства диэлектриков

Для
характеристики тепловых свойств
диэлектриков используются следующие
величины.

Нагревостойкость –
способность электроизоляционных
материалов и изделий без вреда для них
выдерживать воздействие высокой
температуры и резких смен температуры.
Определяют по температуре, при которой
наблюдается существенное изменение
механических и электрических свойств,
например, в органических диэлектриках
начинается деформация растяжения или
изгиба под нагрузкой.

Теплопроводность –
процесс передачи тепла в материале.
Характеризуется экспериментально
определяемым коэффициентом
теплопроводности λ_т. λ_т –
количество теплоты, переданной за одну
секунду через слой материала толщиной
в 1 м и площадью поверхности – 1 м² при
разности температур поверхностей слоя
в 1 °К. Коэффициент теплопроводности
диэлектриков изменяется в широких
пределах. Самые низкие значения λ_т имеют
газы, пористые диэлектрики и жидкости
(для воздуха λ_т =
0,025 Вт/(м·К), для водыλ_т =
0,58 Вт/(м·К)), высокие значения имеют
кристаллические диэлектрики (для
кристаллического кварца λ_т = 12,5 Вт/(м·К)).
Коэффициент теплопроводности диэлектриков
зависит от их строения (для плавленого
кварца λ_т = 1,25 Вт/(м·К))
и температуры.

Тепловое
расширение диэлектриков
оценивают температурным коэффициентом
линейного расширения: .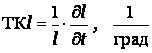
Материалы с малым тепловым расширением,
имеют, как правило, более
высокую нагревостойкость и
наоборот. Тепловое расширение органических
диэлектриков значительно (в десятки и
сотни раз) превышает расширение
неорганических диэлектриков. Поэтому
стабильность размеров деталей из
неорганических диэлектриков при
колебаниях температуры значительно
выше по сравнению с органическими.

1. Абсорбционные
токи

В
общем случае электрический ток j в
диэлектрике представляет собой сумму
сквозного тока j_ск и
тока абсорбции j_аб

j = j_ск + j_аб.

Ток
абсорбции можно определить через ток
смещения j_см –
скорость изменения вектора электрической
индукции D

Сквозной
ток определяется переносом (движением)
в электрическом поле различных носителей
заряда.

2. Электронная электропроводность
характеризуется перемещением электронов
под действием поля. Кроме металлов она
присутствует у углерода, оксидов
металлов, сульфидов и др. веществ, а
также у многих полупроводников.

3. Ионная
– обусловлена
движением ионов. Наблюдается в растворах
и расплавах электролитов – солей,
кислот, щелочей, а также во многих
диэлектриках. Она подразделяется на
собственную и примесную проводимости.
Собственная проводимость обусловлена
движением ионов, получаемых при
диссоциации^[1] молекул.
Движение ионов в электрическом поле
сопровождается электролизом^[2] –
переносом вещества между электродами
и выделением его на электродах. Полярные
жидкости диссоциированы в большей
степени и имеют большую электропроводность,
чем неполярные.

В
неполярных и слабополярных жидких
диэлектриках (минеральные масла,
кремнийорганические жидкости)
электропроводность определяется
примесями.

4. Молионная электропроводность
– обусловлена
движением заряженных частиц,
называемых молионами.
Наблюдают ее в коллоидных системах,
эмульсиях^[3],
суспензиях^[4].
Движение молионов под действием
электрического поля называют электрофорезом.
При электрофорезе, в отличие от
электролиза, новых веществ не образуется,
меняется относительная концентрация
дисперсной фазы в различных слоях
жидкости. Электрофоретическая
электропроводность наблюдается,
например, в маслах, содержащихэмульгированную воду.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Диэлектрическая проницаемость

Диэлектрическая проницаемость и электрическая постоянная

Электрическая постоянная

Диэлектрическая проницаемость вещества

Диэлектрическая проницаемость некоторых веществ

Относительная диэлектрическая проницаемость

Содержание

Измерение

Зависимость от частоты

Примечания

См. также

Значения диэлектрической проницаемости для некоторых веществ

Смотреть что такое «Относительная диэлектрическая проницаемость» в других словарях:

Диэлектрическая проницаемость

Диэлектрическая проницаемость

Абсолютная диэлектрическая проницаемость вакуума[править | править код]

Эффект поляризации диэлектрика и проницаемость[править | править код]

Роль диэлектрической проницаемости среды в физике[править | править код]

Диэлектрическая проницаемость непоглощающей среды[править | править код]

Проницаемость и связанные с ней величины[править | править код]

Проницаемость в оптическом диапазоне частот[править | править код]

Тензор проницаемости анизотропных сред[править | править код]

Статическая проницаемость некоторых диэлектриков[править | править код]

Проницаемость диэлектрической среды с потерями[править | править код]

Комплексная диэлектрическая проницаемость[править | править код]

Характеристика диэлектрических потерь[править | править код]

Типичная частотная зависимость проницаемости[править | править код]

Измерение диэлектрической проницаемости[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как составить акт нужен образец

Как найти приложения для apple watch

Как найти общую жесткость раствора

Добавить комментарий Отменить ответ