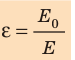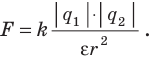По электрическим свойствам все вещества разделяют на два больших класса – вещества, которые проводят электрический ток (проводники) и вещества, которые не проводят электрический ток (диэлектрики, или изоляторы).
Мы знаем, что все вещества состоят из атомов, которые, в свою очередь, состоят из заряженных частиц. Если внешнее поле вокруг вещества отсутствует, то его частицы распределяются так, что суммарное электрическое поле внутри вещества равно нулю. Если вещество поместить во внешнее электрическое поле, то поле начет действовать на заряженные частицы и они перераспределяться так, что в веществе возникнет собственное электрическое поле. Полное электрическое поле складывается из внешнего поля
и внутреннего поля
создаваемого заряженными частицами вещества.
Проводник – это тело или материал, в котором электрические заряды начинают перемещаться под действием сколь угодно малой силы. Поэтому эти заряды называют свободными.
В металлах свободными зарядами являются электроны, в растворах и расплавах солей (кислот и щелочей) – ионы.
Диэлектрик – это тело или материал, в котором под действием сколь угодно больших сил заряды смещаются лишь на малое, не превышающее размеров атома расстояние относительно своего положения равновесия. Такие заряды называются связанными.
Рассмотрим подробнее эти классы веществ.
Проводники в электрическом поле.
Проводниками называют вещества, проводящие электрический ток.
Типичными проводниками являются металлы.
Основная особенность проводников – наличие свободных зарядов ( в металлах это электроны), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами.
Явление перераспределения зарядов внутри проводника под действием внешнего электрического поля называется электростатической индукцией.
Заряды, появляющиеся на поверхности проводника, называются индукционными зарядами.
Индукционные заряды создают свое собственное поле , которое компенсирует внешнее поле
во всем объеме проводника:
(внутри проводника).
Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие электрического тока.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
При внесении диэлектрика во внешнее электрическое поле в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.
Связанные заряды создают электрическое поле , которое внутри диэлектрика направлено противоположно вектору напряженности внешнего поля
. Этот процесс называется поляризацией диэлектрика.
Электрической поляризацией называют особое состояние вещества, при котором электрический момент некоторого объёма этого вещества не равен нулю.
В результате полное электрическое поле внутри диэлектрика оказывается по модулю меньше внешнего поля
.
Физическая величина, равная отношению модуля напряженности внешнего электрического поля в вакууме к модулю напряженности полного поля в однородном диэлектрике
, называется диэлектрической проницаемостью вещества.
Диэлектрическая проницаемость среды показывает, во сколько раз напряженность поля в вакууме больше, чем в диэлектрике. Это величина безразмерная (нет единиц измерения).
При поляризации неоднородного диэлектрика связанные заряды могут возникать не только на поверхностях, но и в объеме диэлектрика. В этом случае электрическое поле связанных зарядов и полное поле
могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле
в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем
строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:
Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд q, то напряженность поля , создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
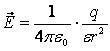
Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная, электронная и ионная поляризации. Ориентационная и электронная механизмы проявляются главным образом при поляризации газообразных и жидких диэлектриков, ионная – при поляризации твердых диэлектриков.
Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников.
Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U.
Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.
Электроемкостью (электрической емкостью) проводников называется физическая величина, характеризующая способность проводника или системы проводников накапливать электрический заряд.
Электроемкость находится как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
В системе СИ единица электроемкости называется фарад [Ф]:
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Простейший конденсатор – плоский конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния.
В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними.
Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.
Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R1 и R2.
Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L.
Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:
– сферический конденсатор
– цилиндрический конденсатор
Для получения заданного значения емкости конденсаторы соединяются между собой, образуя батареи конденсаторов.
1) При параллельном соединении конденсаторов соединяются их одноименно заряженные обкладки.
Напряжения на конденсаторах одинаковы U1 = U2 = U, заряды равны q1 = С1U и q2 = С2U.
Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует или С = С1 + С2
Таким образом, при параллельном соединении электроемкости складываются.
2) При последовательном соединении конденсаторов соединяют разноименно заряженные обкладки
Заряды обоих конденсаторов одинаковы q1 = q2 = q, напряжения на них равны и
Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2.
Следовательно, или
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.
Т.е. в случае n конденсаторов одинаковой емкости С емкость батареи
при параллельном соединении Собщ = nС
при последовательном соединении Собщ = С/n
Если обкладки заряженного конденсатора замкнуть металлическим проводником, то по цепи пойдет электрический ток, лампочка загорится и будет гореть до тех пор, пока конденсатор не разрядится. Значит, заряженный конденсатор содержит запас энергии.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую.При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов
при переносе каждой порции Δq внешние силы должны совершить работу
Энергия We конденсатора емкости C, заряженного зарядом q, может быть найдена путем интегрирования этого выражения в пределах от 0 до q:
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением q = CU.
Электрическую энергию We следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе.
По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.
Для школьников (для лучшего понимания физики).
Вещества, встречающиеся в природе, способны проводить электрический ток в разной степени. По этой способности вещества делятся на проводники, диэлектрики и полупроводники.
Сначала просмотрите предыдущую статью “Зарядка и разрядка конденсатора. Зарядный и разрядный ток проводимости”.
Рассмотрим прежде свойства диэлектрика, влияние внешнего электрического поля (электрического поля конденсатора) на поведение диэлектрика, находящегося между обкладками конденсатора.
Диэлектрик в электрическом поле
Диэлектрики – это вещества, почти не имеющие свободных электронов (в отличие от проводников), поэтому в диэлектрике невозможно появление тока проводимости.
Однако электрическое поле оказывает определённое влияние на диэлектрик, так как в нём есть положительные и отрицательные заряды. Это влияние определяется структурой молекулы диэлектрика.
Чтобы понять поведение диэлектрика в электрическом поле, надо представить себе молекулу диэлектрика.
Все диэлектрики можно разделить на три класса: полярные, неполярные и кристаллические.
Молекула диэлектрика, как и любого вещества, состоит из атомов. Электроны в атомах диэлектрика связаны с ядром атома так, что не могут оторваться от атома (находятся в связанном состоянии).
Но внешнее электрическое поле (пусть это будет поле конденсатора) оказывает действие на заряды, находящиеся внутри молекулы, смещая их в пределах молекулы (положительные заряды смещаются по полю, а отрицательные – против направления поля).
Молекулу диэлектрика можно представить в виде диполя – системы, состоящей из положительного и отрицательного зарядов (равных по модулю), расположенных на расстоянии l друг от друга.
Положительный заряд диполя равен суммарному заряду ядер молекулы диэлектрика, а отрицательный заряд равен суммарному заряду всех электронов молекулы диэлектрика, помещённых в центр масс этих зарядов.
Диполь характеризуется дипольным (электрическим) моментом, равным произведению заряда на расстояние между ними, направленным от отрицательного заряда к положительному:
В молекулах неполярных диэлектриков, к которым относятся молекулы, имеющие симметричное строение (кислород, азот и др.) в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов совпадают и их дипольный момент равен нулю.
Если же включить электрическое поле, то в молекулах неполярного диэлектрика происходит смещение зарядов и молекула приобретает дипольный момент.
Молекулы полярных диэлектриков, к которым относится, например, вода имеют несимметричное строение – их дипольный момент даже в отсутствие поля не равен нулю, но дипольные моменты молекул при этом располагаются хаотично.
Внешнее электрическое поле заставляет из выстраиваться упорядоченно – их дипольные моменты направляются вдоль поля (подробно о диполях и влиянии электрического поля на диэлектрик см. в Занятии 51).
Каким бы ни был диэлектрик, при помещении его в электрическое поле на заряды диполя действует электрическая сила, заставляющая диполи выстраиваться по направлению поля (их дипольный момент окажется направленным по полю).
В результате этого вблизи положительно заряженной обкладки конденсатора окажутся связанные отрицательные заряды, с некоторой плотностью, а вблизи отрицательно заряженной обкладки конденсатора – связанные положительные заряды (см. рисунок ниже).
Внутри диэлектрика связанные положительные и отрицательные заряды компенсируют друг друга, а на гранях диэлектрика они оказываются нескомпенсированными, характеризующимися некоторой плотностью.
Связанные заряды разделить нельзя, так как их смещение происходит в пределах молекулы.
Если просуммировать дипольные моменты всех молекул, находящихся в единице объёма однородного изотропного диэлектрика, то получим вектор поляризации Р диэлектрика (если дипольный момент характеризует молекулу диэлектрика, то вектор поляризации Р показывает поведение единичного объёма диэлектрика в электрическом поле, а через поведение единичного объёма судим о поведении диэлектрика в целом).
Поляризация диэлектрика
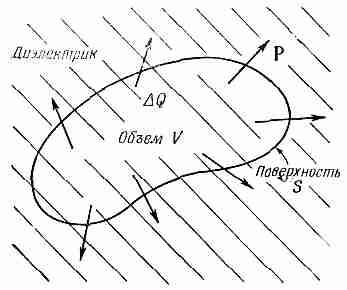
На рисунке показан некоторый объём диэлектрика, его поляризованное состояние.
Направление вектора поляризации Р диэлектрика совпадает с направлением вектора напряжённости электрического поля конденсатора.
На рисунке Ео – есть вектор напряжённости поля конденсатора, которое создаётся зарядами на его обкладках.
Есв – это напряжённость электрического поля, созданного связанными зарядами. Видим, что поле связанных зарядов направлено навстречу внешнему полю Ео, то есть диэлектрик ослабляет внешнее электрическое поле.
Тогда результирующее поле в диэлектрике Е= Ео – Есв, направлено оно вдоль поля Ео, так как поле Есв всегда меньше внешнего поля.
Основной характеристикой диэлектрика является величина
называемая его диэлектрической проницаемостью (находится из таблицы).
Диэлектрическая проницаемость показывает во сколько раз напряжённость электрического поля Е в диэлектрике меньше напряжённости Ео внешнего электрического поля:
(На рисунке показан диэлектрик, занимающий часть объёма между пластинами конденсатора, чтобы лучше понять происходящее).
В виде диэлектрика в конденсаторе можно представить воздух, но ёмкость такого (воздушного) конденсатора очень мала. Чаще всего используют конденсаторы с твёрдыми диэлектриками – такой диэлектрик мы и представляем рассматривая рисунок.
Следующий рисунок аналогичен предыдущему – на нём показаны направления и длины векторов: поля Ео конденсатора, поля Есв связанных зарядов и результирующего поля Е в диэлектрике:
Теперь посмотрим и поясним рисунком, что происходит в кристаллическом диэлектрике, имеющем ионное строение, при его помещении в электрическое поле.
В узлах кристаллической решётки такого диэлектрика находятся положительные и отрицательные ионы. Например, в узлах решётки кристалла каменной соли находятся положительные ионы натрия и отрицательные ионы хлора.
Под действием электрического поля конденсатора отрицательные ионы кристаллической решётки диэлектрика несколько (в пределах размера ячейки кристалла) смещаются в сторону положительной обкладки конденсатора, а положительные ионы – в сторону отрицательной обкладки конденсатора. В результате кристаллическая решётка диэлектрика упруго деформируется.
Такое состояние диэлектрика называется поляризованностью, а само явление смещения связанных зарядов в диэлектрике под действием внешнего электрического поля называется поляризацией диэлектрика.
Если электрическое поле конденсатора убрать, то ионы диэлектрика вернутся в исходное положение и упругая деформация решётки исчезнет.
Диэлектрическая проницаемость диэлектрика “эпсилон” характеризует степень его поляризации – чем она больше, тем сильнее диэлектрик поляризуется (тем больше смещаются связанные заряды от своих положений равновесия).
Смещаясь, связанные заряды создают своё электрическое поле Есв, направленное навстречу внешнему электрическому полю.
Таким образом, в конденсаторе, заполненном диэлектриком, напряжённость электрического поля уменьшается:
Е= Ео – Есв,
значит уменьшается и напряжение между обкладками конденсатора, согласно формуле, связывающей между собой напряжённость и напряжение:
U=E d,
где d – расстояние между обкладками.
Тогда при тех же зарядах q на обкладках конденсатора ёмкость конденсатора в присутствие диэлектрика увеличивается в “эпсилон” раз (числитель остался прежним, знаменатель дроби уменьшился):
С = q / U.
Так объясняется увеличение ёмкости конденсатора, содержащего диэлектрик, по сравнению с ёмкостью того же конденсатора, когда между его обкладками содержится воздух или создан вакуум.
Увеличение ёмкости конденсатора говорит о том, что он способен накопить на обкладках больший заряд при меньшем напряжении, что хорошо, так как при большом напряжении может произойти пробой диэлектрика и конденсатор выйдет из строя.
Понятие тока поляризации
Вернёмся к рассмотрению кристаллической решётки
Рассмотренное смещение положительных ионов решётки в одном направлении, а отрицательных в противоположном при включении электрического поля происходит во всём объёме диэлектрика.
Когда это смещение положительных и отрицательных ионов диэлектрика происходит, через диэлектрик проходит ток. Ведь под током понимается заряд, проходящий через некоторое сечение (сейчас это будет сечение диэлектрика параллельное обкладкам конденсатора) за единицу времени.
Этот ток, созданный упорядоченным смещением связанных зарядов диэлектрика под действием изменяющегося электрического поля, называется током поляризации.
Отметим отличие тока поляризации в диэлектрике от тока проводимости в проводниках?
Ток проводимости создаётся свободными электронами, способными перемещаться по проводнику на значительные расстояния. Ток проводимости существует всё время, пока есть разность потенциалов на концах проводника.
Ток же поляризации создаётся связанными зарядами, которые лишь незначительно (в пределах размера ячейки решётки) смещаются из своих положений равновесия.
Ток поляризации в диэлектрике существует лишь при изменении электрического поля (когда в диэлектрике возникает, усиливается или исчезает электрическое поле).
Если электрическое поле имеет постоянное значение, то и поляризация диэлектрика будет иметь постоянное значение, то есть заряды сместятся на некоторое расстояние, зависящее от величины приложенного напряжения между обкладками конденсатора (или величины напряжённости Ео поля конденсатора), но тока в диэлектрике не будет.
В предыдущей статье нами рассмотрен процесс зарядки конденсатора при его подключении к источнику постоянного тока (или постоянного напряжения) и рассмотрена кривая зависимости зарядного тока проводимости от времени
В процессе зарядки конденсатора зарядный ток проводимости (в проводе цепи) уменьшается, а напряжение между обкладками конденсатора (значит, и напряжённость поля между обкладками) увеличиваются. В это время в диэлектрике имеет место зарядный ток поляризации.
Таким образом, когда в проводе цепи при зарядке конденсатора существует зарядный ток проводимости, в диэлектрике существует зарядный ток поляризации.
Электрическая цепь с конденсатором, содержащая источник постоянного тока, оказывается замкнутой только во время зарядки конденсатора.
Когда конденсатор полностью зарядится (когда его напряжение станет равным напряжению на клеммах источника постоянного тока) конденсатор разрывает цепь (тока в цепи не будет).
К току поляризации мы ещё вернёмся.
Тема следующей статьи “Каким общим свойством обладают ток проводимости и изменяющееся во времени электрическое поле? Ток поляризации”.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Зарядка конденсатора. Зарядный и разрядный ток проводимости.
Следующая запись:Какое одинаковое свойство имеют изменяющееся во времени электрическое поле и ток проводимости? Ток поляризации.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Глава 10
ДИЭЛЕКТРИКИ
§1. Диэлектрическая проницаемость
§2. Вектор поляризации Р
§З. Поляризационные заряды
§4. Уравнения электростатики для диэлектриков
§5. Поля и силы в присутствии диэлектриков
§ 1. Диэлектрическая проницаемость
Сейчас мы разберем еще одно характерное свойство материи, возникающее под влиянием электрического поля. В одной из предыдущих глав мы рассмотрели поведение проводников, в которых заряды под влиянием электрического поля свободно текут в такие участки, что поле внутри проводника обращается в нуль. Теперь мы будем говорить об изоляторах, т. е. таких материалах, которые не проводят электричество. Сначала можно было бы подумать, что в них вообще ничего не происходит. Но Фарадей с помощью простого электроскопа и конденсатора, состоящего из двух параллельных пластин, обнаружил, что это не так. Его опыт показал, что если между пластинами поместить изолятор, то емкость такого конденсатора увеличится. Когда изолятор целиком заполняет пространство между пластинами, емкость возрастает в x раз, причем x зависит только от свойств изолирующего материала. Изолирующие материалы называют также диэлектриками; тогда множитель x характеризует свойства диэлектрика и называется диэлектрической проницаемостью. Диэлектрическая проницаемость вакуума, конечно, равна единице.
Наша задача теперь состоит в том, чтобы объяснить, почему вообще возникает электрический эффект, раз изоляторы фактически являются изоляторами и не проводят электричества. Начнем с экспериментального факта, что емкость увеличивается, и попытаемся разобраться, что же там может происходить. Рассмотрим плоский конденсатор, на проводящих пластинах которого имеются заряды, скажем, на верхней пластине отрицательные, а на нижней — положительные.
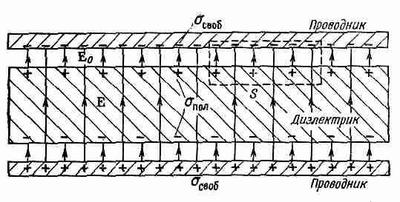
Фиг. 10.1. Плоский конденсатор с диэлектриком. Показаны линии паяя E.
Пусть расстояние между пластинами равно d, а площадь каждой пластины А. Как мы показали раньше, емкость равна
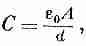
(10.1)
а заряд и потенциал конденсатора связаны соотношением
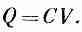
(10.2)
Далее, экспериментальный факт состоит в том, что если мы положим между пластинами кусок изолирующего материала, например стекла или плексигласа, то емкость возрастет. Это, разумеется, означает, что при том же заряде потенциал стал меньше. Но разность потенциалов есть интеграл от электрического поля, взятый поперек конденсатора; отсюда мы должны заключить, что электрическое поле внутри конденсатора стало меньше, хотя заряды пластин и не изменились.
Но как может это быть? Нам известна теорема Гаусса, которая утверждает, что полный поток электрического поля прямо связан с находящимся внутри объема электрическим зарядом. Рассмотрим входящую в теорему Гаусса поверхность S, изображенную пунктиром на фиг. 10.1. Поскольку электрическое поле в присутствии диэлектрика уменьшается, мы заключаем, что полный заряд внутри поверхности должен теперь быть меньше, чем до внесения изолятора. Остается сделать единственный вывод, что на поверхности диэлектрика должны находиться положительные заряды. Раз поле уменьшилось, но все же не обратилось в нуль, значит, этот положительный заряд меньше отрицательного заряда в проводнике. Итак, явление это можно объяснить, если мы поймем, почему на одной поверхности диэлектрика, помещенного в электрическое поле, индуцируется положительный заряд, а на другой — отрицательный.
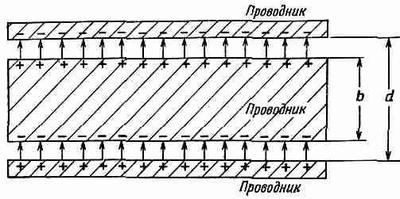
Фиг. 10.2. Если поместить пластинку проводника внутрь плоского конденсатора, наведенные заряды обратят поле в проводнике в нуль.
Все было бы понятно, если бы речь шла о проводнике. Пусть у нас был бы, например, конденсатор, расстояние между пластинами которого равно d, и мы вставили бы между этими пластинами незаряженный проводник толщиной b (фиг. 10.2). Электрическое поле индуцирует положительный заряд на верхней поверхности и отрицательный заряд на нижней поверхности, так что в результате поле внутри проводника погашается. Во всех остальных местах поле такое же, какое было без проводника, поэтому оно равно поверхностной плотности зарядов, деленной на eо; но расстояние, по которому мы должны интегрировать, чтобы получить напряжение (разность потенциалов), стало меньше.
Напряжение равно
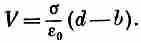

Окончательное выражение для емкости похоже на (10.1), где d нужно заменить разностью (d-b):
(10.3)
Емкость увеличилась в некоторое число раз, зависящее от b/d, доли объема, занятого проводником.
Отсюда мы получаем модель того, что происходит в диэлектриках: внутри материала имеется множество мелких проводящих слоев. Беда такой модели состоит в том, что в ней должна иметься выделенная ось — перпендикуляр ко всем слоям, а у большинства диэлектриков такой оси нет.
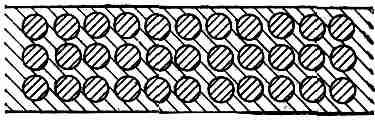
Фиг. 10.3. Модель диэлектрика; маленькие проводящие шарики, вставленные внутрь идеального изолятора.
Эту трудность, однако, можно устранить, предположив, что все изолирующие материалы содержат маленькие проводящие шарики, отделенные один от другой изолятором (фиг. 10.3). Появление диэлектрической проницаемости тогда объясняется действием зарядов, индуцируемых в каждом шарике. В этом и состоит одна из самых первых физических моделей диэлектриков, предложенная для объяснения явления, которое наблюдал Фарадей. Точнее, предполагалось, что каждый атом материала есть идеальный проводник, изолированный от остальных атомов. Диэлектрическая проницаемость x тогда должна была определяться долей того объема, который занимают проводящие шарики. Теперь, однако, пользуются другой моделью.
§ 2. Вектор поляризации Р
Продолжив наш анализ, мы обнаружим, что идея о проводящих и непроводящих участках не так уж существенна. Любой из маленьких шариков действует как диполь, момент которого создается внешним полем. Для понимания диэлектриков существенной является идея о том, что в материале возбуждается множество маленьких диполей. Почему они возбуждаются — то ли потому, что в материале есть проводящие шарики, то ли по каким-либо другим причинам — абсолютно несущественно.
Почему поле должно индуцировать дипольный момент у атома, хотя атом не является проводящим шариком? Мы обсудим этот вопрос гораздо подробнее в следующей главе, которая будет посвящена внутреннему механизму диэлектрических материалов. А сейчас мы дадим лишь один пример, только чтобы проиллюстрировать возможный механизм. Атом имеет ядро с положительным зарядом, окруженное отрицательными электронами. В электрическом поле ядро притягивается в одну сторону, а электроны в другую. Орбиты или плотности вероятности электронов (или какая-либо другая картина, используемая в квантовой механике) несколько искажаются (фиг. 10.4); центр тяжести отрицательных зарядов сместится и больше не будет совпадать с положительным зарядом ядра. Мы уже обсуждали такое распределение заряда. Если взглянуть на него издалека, то подобная нейтральная конфигурация в первом приближении эквивалентна маленькому диполю.
Если поле не чересчур велико, естественно считать величину индуцированного дипольного момента пропорциональной полю. Иначе говоря, небольшое поле сместит заряды чуть-чуть, а более сильное поле раздвинет их дальше — пропорционально величине поля, пока смещение не станет чересчур большим.
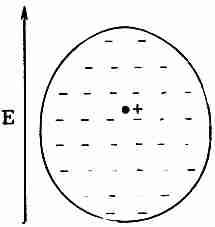
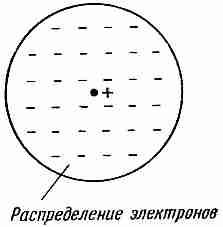
Фиг. 10.4. Распределение электронов атома в электрическом поле сдвигается относительно ядра.
До конца этой главы мы будем считать, что дипольный момент в точности пропорционален полю.
Предположим теперь, что в каждом атоме заряды q разделены промежутком d, так что qd есть дипольный момент одного атома. (Мы пишем d, потому что d уже использовано для обозначения расстояния между пластинами.) Если в единице объема имеется N атомов, то дипольный момент в единице объема равен Nqd. Этот дипольный момент в единице объема мы запишем в виде вектора Р. Нет необходимости подчеркивать, что он лежит в направлении всех отдельных дипольных моментов, т. е. в направлении смещения зарядов d:
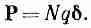
(10.4)
Вообще говоря, Р будет меняться в диэлектрике от точки к точке. Но в каждой точке Р пропорционален электрическому полю Е. Константа пропорциональности, которая определяется тем, насколько легко можно сместить электрон, зависит от сорта атомов в материале.
О том, что действительно определяет поведение этой константы и степень ее постоянства для больших полей, а также о том, что происходит внутри разных материалов, мы поговорим позже. А пока мы просто предположим, что существует какой-то механизм, благодаря которому индуцируется дипольный момент, пропорциональный электрическому полю.
§ 3. Поляризационные заряды
Посмотрим теперь, что дает эта модель для конденсатора с диэлектриком. Рассмотрим сначала лист материала, в котором на единицу объема приходится дипольный момент Р. Получится ли в результате в среднем какая-нибудь плотность зарядов? Нет, если Р постоянен.
Если положительные и отрицательные заряды, смещенные относительно друг друга, имеют одну и ту же среднюю плотность, то сам факт их смещения не приводит к появлению суммарного заряда внутри объема. С другой стороны, если бы Р в одном месте был больше, а в другом меньше, то это означало бы, что в некоторые области попало больше зарядов, чем оттуда вышло; тогда мы бы могли получить объемную плотность заряда. В случае плоского конденсатора предположим, что Р — величина постоянная, поэтому достаточно будет только посмотреть, что происходит на поверхностях. На одной поверхности отрицательные заряды (электроны) эффективно выдвинулись на расстояние d, а на другой поверхности они сдвинулись внутрь, оставив положительные заряды снаружи на эффективном расстоянии d. Возникает, как показано на фиг. 10.5, поверхностная плотность зарядов, которую мы будем называть поляризационным зарядом.
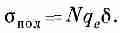
Этот заряд можно подсчитать следующим образом. Если площадь пластинки равна А, то число электронов, которое окажется на поверхности, есть произведение А и N (числа электронов на единицу объема), а также смещения S, которое, как мы предполагаем, направлено перпендикулярно к поверхности. Полный заряд получится умножением на заряд электрона qe. Чтобы найти поверхностную плотность поляризационных зарядов, индуцируемую на поверхности, разделим на А. Величина поверхностной плотности зарядов равна
Но она равна как раз длине Р вектора поляризации Р [формула (10.4)]:
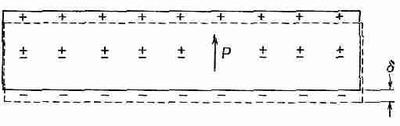
Фиг. 10.5. Диэлектрик в однородном поле. Положительные заряды сместились на расстояние d относительно отрицательных.

(10.5)
Поверхностная плотность зарядов равна поляризации внутри материала. Поверхностный заряд, конечно, на одной поверхности положителен, а на другой отрицателен.
Предположим теперь, что наша пластинка служит диэлектриком в плоском конденсаторе. Пластины конденсатора также имеют поверхностный заряд (который мы обозначим sсвоб, потому что заряды в проводнике могут двигаться «свободно» куда угодно). Конечно, это тот самый заряд, который мы сообщили конденсатору при его зарядке. Следует подчеркнуть, что sпол существует только благодаря sсвоб. Если, разрядив конденсатор, удалить sсвоб, то sпол также исчезнет, но он не стечет по проволоке, которой разряжают конденсатор, а уйдет назад внутрь материала, за счет релаксации поляризации в диэлектрике.
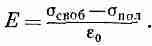
Теперь мы можем применить теорему Гаусса к поверхности S, изображенной на фиг. 10.1. Электрическое поле Е в диэлектрике равно полной поверхностной плотности зарядов, деленной на e0. Очевидно, что sпол и sсвоб имеют разные знаки, так что
(10.6)
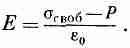
Заметьте, что поле Е0между металлической пластиной и поверхностью диэлектрика больше поля Е; оно соответствует только sсвоб. Но нас здесь интересует поле внутри диэлектрика, которое занимает почти весь объем, если диэлектрик заполняет почти весь промежуток между пластинами. Используя формулу (10.5), можно написать
(10.7)
Из этого уравнения мы не можем определить электрическое поле, пока не узнаем, чему равно Р. Здесь мы, однако, предполагаем, что Р зависит от Е и, более того, пропорционально Е. Эта пропорциональность обычно записывается в виде
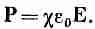
(10.8)
Постоянная c (греческое «хи») называется диэлектрической восприимчивостью диэлектрика.
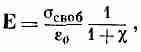
Тогда выражение (10.7) приобретает вид
(10.9)
откуда мы получаем множитель 1/(1+c), показывающий, во сколько раз уменьшилось поле.
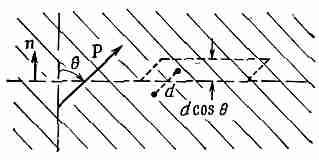
Фиг.10.6. Количество ааряда, прошедшее через элемент воображаемой поверхности в диэлектрике, пропорционально компоненте Р, нормальной к поверхности.
Напряжение между пластинами есть интеграл от электрического поля. Раз поле однородно, интеграл сводится просто к произведению Е и расстояния между пластинами d. Мы получаем
Полный заряд конденсатора есть sсвоб А, так что емкость, определяемая формулой (10.2), оказывается равной
(10.10)
Мы объяснили явление, наблюдавшееся на опыте. Если заполнить плоский конденсатор диэлектриком, емкость возрастает на множитель
(10.11)
который характеризует свойства данного материала. Наше объяснение останется, конечно, неполным, пока мы не объясним (а это мы сделаем позже), как возникает атомная поляризация.
Обратимся теперь к чуть более сложному случаю — когда поляризация Р не всюду одинакова. Мы уже говорили, что если поляризация непостоянна, то вообще может возникнуть объемная плотность заряда, потому что с одной стороны в маленький элемент объема может войти больше зарядов, чем выйдет с другой. Как определить, сколько зарядов теряется или приобретается в маленьком объеме?
Подсчитаем сначала, сколько зарядов проходит через воображаемую плоскость, когда материал поляризуется. Количество заряда, проходящее через поверхность, есть просто Р, умноженное на площадь поверхности, если поляризация направлена по нормали к поверхности. Разумеется, если поляризация касательна, к поверхности, то через нее не пройдет ни одного заряда.
Продолжая прежние рассуждения, легко понять, что количество заряда, прошедшее через любой элемент поверхности, пропорционально компоненте Р, перпендикулярной к поверхности. Сравним фиг. 10.6 и 10.5. Мы видим, что уравнение (10.5) в общем случае должно быть записано так:
(10.12)
Фиг. 10.7. Неоднородная поляризация Р может приводить к появлению результирующего заряда внутри диэлектрика.
Если мы имеем в виду воображаемый элемент поверхности внутри диэлектрика, то формула (10.12) дает заряд, который прошел через поверхность, но не приводит к результирующему поверхностному заряду, потому что возникают равные и противоположно направленные вклады от диэлектрика по обе стороны поверхности.
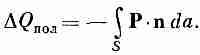
Однако смещение зарядов может привести к появлению объемной плотности зарядов. Полный заряд, выдвинутый из объема V за счет поляризации, есть интеграл от внешней нормальной составляющей Р по поверхности S, охватывающей объем (фиг. 10.7). Такой же излишек зарядов противоположного знака остается внутри. Обозначая суммарный заряд внутри F через DQпол, запишем
(10.13)
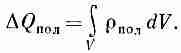
Мы можем отнести DQпол за счет объемного распределения заряда с плотностью rпол, так что
(10.14)
Комбинируя оба уравнения, получаем
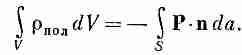
(10.15)
Мы получили разновидность теоремы Гаусса, связывающую плотность заряда поляризованного материала с вектором поляризации Р. Мы видим, что она согласуется с результатом, полученным для поверхностного поляризационного заряда или же для диэлектрика в плоском конденсаторе. Уравнение (10.15) с гауссовой поверхностью S, изображенной на фиг. 10.1, дает в правой части интеграл по поверхности, равный РDA, а в левой части заряд внутри объема оказывается sпол DA, так что мы снова получаем s=Р.
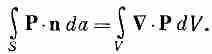
Точно так же, как мы делали в случае закона Гаусса для электростатики, мы можем перейти в уравнении (10.15) к дифференциальной форме, пользуясь математической теоремой Гаусса:
Мы получаем
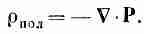
(10.16)
Если поляризация неоднородна, ее дивергенция определяет появляющуюся в материале результирующую плотность зарядов. Подчеркнем, что это совсем настоящая плотность зарядов; мы называем ее «поляризационным зарядом», только чтобы помнить, откуда она взялась.
§ 4. Уравнения электростатики для диэлектриков
Давайте теперь свяжем полученные нами результаты с тем, что мы уже узнали в электростатике. Основное уравнение имеет вид
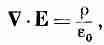
(10.17)
где r — плотность всех электрических зарядов. Поскольку уследить за поляризационными зарядами непросто, удобно разбить r на две части. Обозначим снова через rпол заряды, появляющиеся за счет неоднородной поляризации, а остальную часть назовем rсвоб. Обычно rсвоб означает заряд, сообщаемый проводникам или распределенный известным образом в пространстве. В этом случае уравнение (10.17) приобретает вид
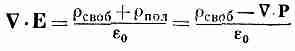
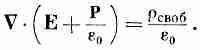
или
(10.18)
Уравнение для ротора от Е, конечно, не меняется:
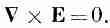
(10.19)

Подставляя Р из уравнения (10.8), получаем более простое уравнение:
(10.20)
Это и есть уравнения электростатики в присутствии диэлектриков. Они, конечно, не дают ничего нового, но имеют вид, более удобный для расчетов в тех случаях, когда rсвоб известно, а поляризация Р пропорциональна Е.
Заметьте, что мы не вытащили «константу» диэлектрической проницаемости x за знак дивергенции. Это потому, что она может не быть всюду одинаковой. Если она повсюду одинакова, то ее можно выделить в качестве множителя и уравнения станут в точности обычными уравнениями электростатики, где только rсвоб нужно поделить на x. В написанной нами форме уравнения годятся в общем случае, когда в разных местах поля расположены разные диэлектрики. В таких случаях решить уравнения иногда бывает очень трудно.
Здесь следует отметить один момент, имеющий историческое значение. На заре рождения электричества атомный механизм поляризации не был еще известен и о существовании rпол не знали. Заряд rсвоб считался равным всей плотности зарядов. Чтобы придать уравнениям Максвелла простой вид, вводили новый вектор D как линейную комбинацию Е и Р:
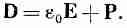
(10.21)
В результате уравнения (10.18) и (10.19) записывались в очень простом виде:
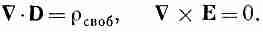
(10.22)
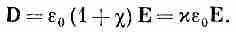
Можно ли их решить? Только когда задано третье уравнение, связывающее D и Е. Если справедливо уравнение (10.8), то эта связь есть
(10.23)
Последнее уравнение обычно записывается так:
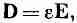
(10.24)
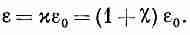
где e — еще одна постоянная, описывающая диэлектрические свойства материалов. Она также называется «проницаемостью». (Теперь вы понимаете, почему в наших уравнениях появилось e0, это «проницаемость пустого пространства».) Очевидно.
(10.25)
Сейчас мы рассматриваем эти вещи уже с другой точки зрения, а именно что в вакууме всегда имеются самые простые уравнения, и если в каждом случае учесть все заряды, какова бы ни была причина их возникновения, то они всегда справедливы. Выделяя часть зарядов либо из соображений удобства, либо потому, что мы не хотим вникать в детали процесса, мы всегда можем при желании написать уравнения в любой удобной для нас форме.
Сделаем еще одно замечание. Уравнение D = eЕ представляет собой попытку описать свойства вещества. Но вещество исключительно сложно по своей природе, и подобное уравнение на самом деле неправильно. Так, если Е становится очень большим, D перестает быть пропорциональным Е. В некоторых веществах пропорциональность нарушается уже при достаточно слабых полях. Кроме того, «константа» пропорциональности может зависеть от того, насколько быстро Е меняется со временем. Следовательно, уравнение такого типа есть нечто вроде приближенного уравнения типа закона Гука. Оно не может быть глубоким, фундаментальным уравнением. С другой стороны, наши основные уравнения для Е (10.17) и (10.19) выражают наиболее полное и глубокое понимание электростатики.
§ 5. Поля и силы в присутствии диэлектриков
Мы докажем сейчас ряд довольно общих теорем электростатики для тех случаев, когда имеются диэлектрики. Мы уже видели, что емкость плоского конденсатора при заполнении его диэлектриком увеличивается в определенное число раз. Сейчас можно показать, что это верно для емкости любой формы, если вся область вокруг двух проводников заполнена однородным линейным диэлектриком. В отсутствие диэлектрика уравнения, которые требуется решить,

такие:
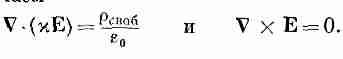
Когда имеется диэлектрик, первое из этих уравнений изменяется, и мы получаем
(10.26)
Далее, поскольку мы считаем и всюду одинаковой, последние два уравнения можно записать в виде

(10.27)
Следовательно, для хЕ получаются такие же уравнения, как для Е0, и тогда они имеют решение хЕ = Е0. Другими словами, поле всюду в х раз меньше, чем в отсутствие диэлектрика. Поскольку разность потенциалов есть линейный интеграл от поля, она уменьшится во столько же раз. А так как заряд на электродах конденсатора в обоих случаях тот же самый, то уравнение (10.2) говорит, что емкость в присутствии всюду однородного диэлектрика увеличивается в х раз.
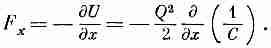
Зададимся теперь вопросом, как взаимодействуют два заряженных проводника в диэлектрике. Рассмотрим жидкий диэлектрик, повсюду однородный. Мы уже видели раньше, что один из способов найти силу — это продифференцировать энергию по соответствующему расстоянию. Если заряды на проводниках равны и противоположны по знаку, то энергия U — QZ/2C, где С — их емкость. С помощью принципа виртуальной работы любая компонента силы получается некоторым дифференцированием; например,
(10.28)
Поскольку диэлектрик увеличивает емкость в х раз, все силы уменьшатся в такое же число раз.
Однако все это не так просто. Сказанное справедливо, только если диэлектрик жидкий. Любое перемещение проводников, окруженных твердым диэлектриком, изменяет условия механических напряжений в диэлектрике и его электрические свойства, а также несколько меняет механическую энергию диэлектрика. Движение проводников в жидкости не меняет свойств жидкости. Жидкость перетекает в другое место, но ее электрические свойства остаются неизменными.
Во многих старых книгах по электричеству изложение начинается с «основного» закона, по которому сила, действующая между двумя зарядами, есть
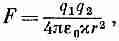
(10.29)
а эта точка зрения абсолютно неприемлема. Во-первых, это не всегда верно; это справедливо только в мире, заполненном жидкостью; во-вторых, так получается лишь для постоянного значения х, что для большинства реальных материалов выполняется приближенно.
Гораздо легче начинать со всегда справедливого (для неподвижных зарядов) закона Кулона для зарядов в вакууме.
Что же происходит с зарядами в твердом теле? На это трудно ответить, потому что даже не вполне ясно, о чем идет речь. Если вы вносите заряды внутрь твердого диэлектрика, то возникают всякого рода давления и напряжения. Вы не можете считать работу виртуальной, не включив сюда также механическую энергию, необходимую для сжатия тела, а отличить однозначным образом электрические силы от механических, возникающих за счет самого материала, вообще говоря, очень трудно. К счастью, никому на самом деле не бывает нужно знать ответ на предложенный вопрос. Иногда нужно знать величину натяжений, которые могут возникнуть в твердом теле, а это можно вычислить. Но результаты здесь оказываются гораздо сложнее, чем простой ответ, полученный нами для жидкостей.
Неожиданно сложной оказывается следующая проблема в теории диэлектриков: почему заряженное тело подбирает маленькие кусочки диэлектрика? Если вы в сухой день причесываетесь, то ваша расческа потом легко будет подбирать маленькие кусочки бумаги. Если вы не вдумались в этот вопрос, то, вероятно, сочтете, что на расческе заряды одного знака, а на бумаге противоположного. Но бумага ведь была сначала электрически нейтральной. У нее нет суммарного заряда, а она все же притягивается. Правда, иногда бумажки подскакивают к расческе, а затем отлетают, сразу же отталкиваясь от нее. Причина, конечно, заключается в том, что, коснувшись расчески, бумага сняла с нее немного отрицательных зарядов, а одноименные заряды отталкиваются. Но это все еще не дает ответа на первоначальный вопрос. Прежде всего, почему бумажки вообще притягиваются к расческе?
Ответ заключается в поляризации диэлектрика, помещенного в электрическое поле. Возникают поляризационные заряды обоих знаков, притягиваемые и отталкиваемые расческой. Однако в результате получается притяжение, потому что поле поблизости от расчески сильнее, чем вдали от нее, ведь расческа не бесконечна. Ее заряд локализован. Нейтральный кусочек бумаги не притянется ни к одной из параллельных пластин конденсатора. Изменение поля составляет существенную часть механизма притяжения.
Как показано на фиг. 10.8, диэлектрик всегда стремится из области слабого поля в область, где поле сильнее. В действительности можно показать, что сила, действующая на малые объекты, пропорциональна градиенту квадрата электрического поля. Почему она зависит от квадрата поля? Потому что индуцированные поляризационные заряды пропорциональны полям, а для данных зарядов силы пропорциональны полю. Однако, как мы уже указывали, результирующая сила возникает, только если квадрат поля меняется от точки к точке. Следовательно, сила пропорциональна градиенту квадрата поля. Константа пропорциональности включает помимо всего прочего еще диэлектрическую проницаемость данного тела и зависит также от размеров и формы тела.
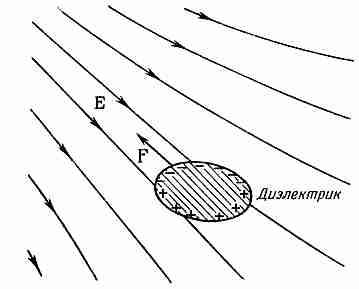
Фиг. 10.8, На диэлектрик в неоднородном поле действует сила, направленная в сторону областей с большей напряженностью поля.
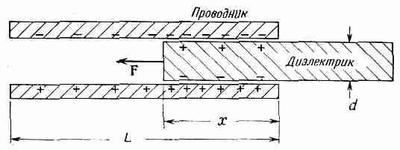
Фиг. 10.9. Сила, действующая на диэлектрик в плоском конденсаторе, может быть вычислена с помощью закона сохранения энергии.
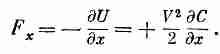
Есть еще одна близкая задача, в которой сила, действующая на диэлектрик, может быть найдена точно. Если мы возьмем плоский конденсатор, в котором плитка диэлектрика задвинута лишь частично (фиг. 10.9), то возникнет сила, вдвигающая диэлектрик внутрь. Провести детальное исследование силы очень трудно; оно связано с неоднородностями поля вблизи концов диэлектрика и пластин. Однако если мы не интересуемся деталями, а просто используем закон сохранения энергии, то силу легко вычислить. Мы можем определить силу с помощью ранее выведенной формулы. Уравнение (10.28) эквивалентно
(10.30)
Нам осталось только найти, как меняется емкость в зависимости от положения плитки диэлектрика.
Пусть полная длина пластин есть L, ширина их равна W, расстояние между пластинами и толщина диэлектрика равна d, а расстояние, на которое вдвинут диэлектрик, есть х. Емкость есть отношение полного свободного заряда на пластинах к разности потенциалов между пластинами. Выше мы видели, что при данном потенциале V поверхностная плотность свободных зарядов равна
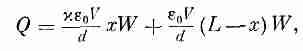
xe0V/d. Следовательно, полный заряд пластин равен
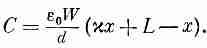
откуда мы находим емкость
(10.31)
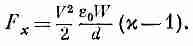
С помощью (10.30) получаем
(10.32)
Но пользы от этого выражения не очень много, разве только вам понадобится определить силу именно в таких условиях. Мы хотели лишь показать, что можно подчас избежать страшных осложнений при определении сил, действующих на диэлектрики, если пользоваться энергией, как это было в настоящем случае.
В нашем изложении теории диэлектриков мы имели дело только с электрическими явлениями, принимая как факт, что поляризация вещества пропорциональна электрическому полю. Почему возникает такая пропорциональность — вопрос, представляющий, пожалуй, еще больший интерес для физики. Стоит нам понять механизм возникновения диэлектрической проницаемости с атомной точки зрения, как мы сможем использовать измерения диэлектрической проницаемости в изменяющихся условиях для получения подробных сведений о строении атомов и молекул. Эти вопросы будут частично изложены в следующей главе.
Внесение некоторого вещества в электрическое поле может привести к существенному его изменению; это обусловлено тем, что вещество составляют заряженные частицы. Если внешнее поле отсутствует, распределение частиц вещества происходит таким образом, что электрическое поле, которое они создают, в среднем по объемам, включающим большое число атомов или молекул, равно нулю. Если внешнее поле присутствует, заряженные частицы перераспределяются, и в веществе возникает собственное электрическое поле. Полное электрическое поле E→ включает в себя (согласно принципу суперпозиции) внешнее поле E0→ и внутреннее поле E’→ которое создается заряженными частицами вещества.
Электрические свойства веществ обуславливают их многообразие. Самые широкие классы веществ – это проводники и диэлектрики.
Проводники
Отличительная черта проводников заключается в наличии свободных зарядов (электронов), принимающих участие в тепловом движении и способных осуществлять перемещение по всему объему проводника. Типичным примером проводников служат металлы.
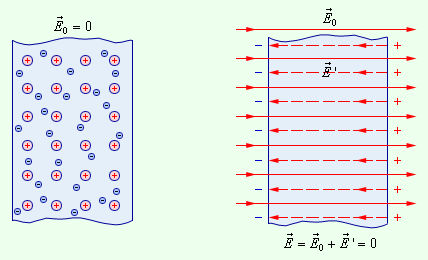
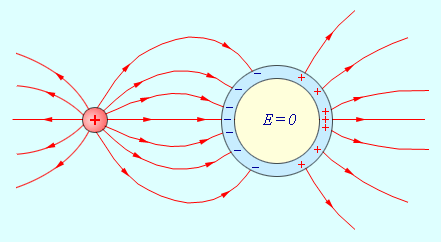
Если внешнее поле отсутствует, то в любом элементе объема проводника отрицательный свободный заряд будет компенсироваться положительным зарядом ионной решетки. В проводнике, который внесен в электрическое поле, произойдет перераспределение свободных зарядов, следствием чего будет возникновение на поверхности проводника нескомпенсированных положительных и отрицательных зарядов (рис. 1.5.1). Описанный процесс носит название электростатической индукции, а возникающие на поверхности проводника заряды называют индукционными зарядами.
Индукционными зарядами создается свое собственное поле E’→ и оно компенсирует внешнее поле E0→ во всем объеме проводника: E→=E0→+E’→=0 (внутри проводника).
Полное электростатическое поле внутри проводника есть нуль, а потенциалы во всех точках являются одинаковыми и равными потенциалу на поверхности проводника.
Рисунок 1.5.1. Электростатическая индукция.
Все внутренние области проводника, который внесен в электрическое поле, остаются электронейтральными. Удаление некоторого объема, выделенного внутри проводника, а соответственно образование пустой полости, приведет к тому, что электрическое поле внутри полости станет равным нулю. На этом основана электростатическая защита – приборы, имеющие чувствительность к электрическому полю в целях исключения влияния поля помещают в металлические ящики (рис. 1.5.2).
Рисунок 1.5.2. Схема электростатической защиты. Поле в металлической полости равно нулю.
Поскольку поверхность проводника эквипотенциальна, необходимо, чтобы силовые линии у поверхности являлись перпендикуляром к ней.
Диэлектрики
Диэлектрики (изоляторы) отличаются от проводников тем, что не имеют свободных электрических зарядов. Диэлектрики включают в себя нейтральные атомы или молекулы. Заряженные частицы в нейтральном атоме являются связанными друг с другом и не имеют способности к перемещению под действием электрического поля по всему объему диэлектрика.
Внесение диэлектрика во внешнее электрическое поле E0→ вызовет возникновение в нем некоторого перераспределения зарядов, которые входят в состав атомов или молекул. Следствием этого перераспределения является появление на поверхности диэлектрического образца избыточных нескомпенсированных связанных зарядов. Все заряженные частицы, которые образуют макроскопические связанные заряды, все так же входят в состав своих атомов.
Связанные заряды образуют электрическое поле E’→ направленное внутри диэлектрика противоположно вектору напряженности E0→ внешнего поля: данный процесс носит название поляризации диэлектрика.
Вследствие поляризации полное электрическое поле E→=E0→+E’→=0 внутри диэлектрика становится по модулю меньше внешнего поля E0→.
Диэлектрическая проницаемость вещества – это физическая величина, которая есть отношение модуля напряженности E0→ внешнего электрического поля, создаваемого в вакууме, к модулю напряженности E→ полного поля в однородном диэлектрике.
ε=E0E.
Известно несколько механизмов поляризации диэлектриков: основные – это ориентационная и электронная поляризации. Проявление этих механизмов происходит в основном при поляризации газообразных и жидких диэлектриков.
Ориентационная или дипольная поляризация появляется, когда полярные диэлектрики состоят из молекул, у которых имеет место несовпадение центов распределения положительных и отрицательных зарядов. Такие молекулы представляют собой микроскопические электрические диполи.
Микроскопические электрические диполи – это нейтральная совокупность двух зарядов, являющихся равными по модулю и противоположными по знаку, расположенных на расстоянии друг от друга.
К примеру, дипольный момент имеет молекула воды, а также молекулы некоторых прочих диэлектриков (H2S, NO2 и т. д.).
Когда внешнее электрическое поле отсутствует, оси молекулярных диполей по причине теплового движения имеют хаотичную ориентацию, в связи с чем на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем является равным нулю.
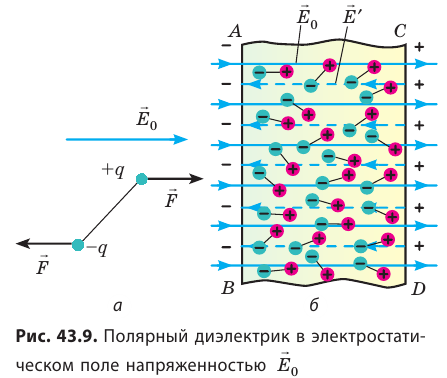
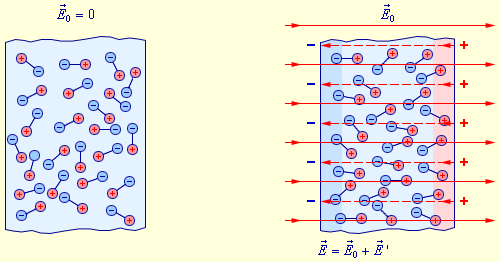
Если внести диэлектрик во внешнее поле E0→, возникнет частичная ориентация молекулярных диполей. Вследствие этого поверхность диэлектрика получит нескомпенсированные макроскопические связанные заряды, создающие поле E’→ направленное навстречу внешнему полю E0→ (рис. 1.5.3).
Рисунок 1.5.3. Ориентационный механизм поляризации полярного диэлектрика.
Поляризация полярных диэлектриков обладает сильной зависимостью от температуры, поскольку тепловое движение молекул выступает в качестве дезориентирующего фактора.
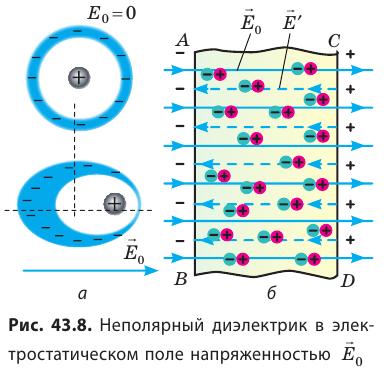
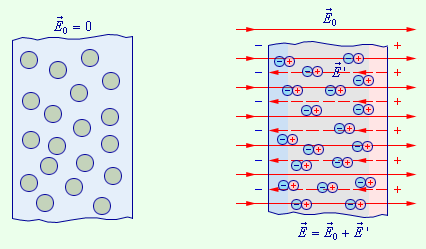
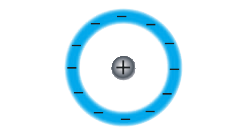
Электронный или упругий механизм возникает при поляризации неполярных диэлектриков, молекулы которых не имеют при отсутствии внешнего поля дипольного момента. Электрическое поле, воздействуя на молекулы неполярных диэлектриков, вызывает их деформацию – положительные заряды смещаются в направлении вектора E0→ а отрицательные – в противоположном направлении. В итоге каждая молекула становится электрическим диполем, ось которого имеет направление вдоль внешнего поля. Поверхность диэлектрика получает нескомпенсированные связанные заряды, которые создают свое поле E’→ имеющее направление навстречу внешнему полю E0→ Таким образом происходит поляризация неполярного диэлектрика (рис. 1.5.4).
Деформация неполярных молекул, испытывающих влияние внешнего электрического поля, не имеет зависимости от теплового движения, т.е. поляризация неполярного диэлектрика не зависит от температуры.
В качестве примера неполярной молекулы можно рассмотреть молекулу метана CH4, в которой четырехкратно ионизированный ион углерода C4– расположен в центре правильной пирамиды; в вершинах этой пирамиды – ионы водорода H+. Наложение внешнего электрического поля вызовет смещение иона углерода из центра пирамиды: в этом случае у молекулы возникнет дипольный момент, пропорциональный внешнему полю.
Рисунок 1.5.4. Поляризация неполярного диэлектрика.
В электрическом поле E’→ связанных зарядов, которое возникает при поляризации полярных и неполярных диэлектриков, происходит его изменение по модулю прямо пропорционально модулю внешнего поля E0→. В электрических полях значительной силы указанная закономерность может нарушаться: в таком случае получают проявление различные нелинейные эффекты. Для полярных диэлектриков в сильных полях возможно наблюдать эффект насыщения.
Эффект насыщения – это выстраивание всех молекулярных диполей вдоль силовых линий.
Когда диэлектрики неполярны, сильное внешнее поле, которое можно сравнить по модулю с внутриатомным полем, имеет возможность значимо деформировать атомы или молекулы вещества с изменением их электрических свойств. Но подобные явления почти никогда не наблюдаются, поскольку для этого необходимы поля, имеющие напряженность порядка 1010–1012 В/м. При этом гораздо раньше наступает электрический пробой диэлектрика.
Электронная поляризация – это процесс поляризации, при котором непарные молекулы получают деформацию электронных оболочек.
Этот механизм универсален, так как деформация электронных оболочек под влиянием внешнего поля происходит в атомах, молекулах и ионах любого диэлектрика.
Ионная поляризация – это поляризация твердых кристаллических диэлектриков, следствием которой является смещение ионов различных знаков, составляющих кристаллическую решетку, в противоположных направлениях при воздействии внешнего поля. В результате смещения на гранях кристалла образуются связанные (нескомпенсированные) заряды.
В качестве примера описанного механизма, можно рассмотреть поляризацию кристалла NaCl, в котором ионы Na+ и Cl– составляют две подрешетки, вложенные друг в друга. При отсутствии внешнего поля каждая элементарная ячейка кристалла NaCl является электронейтральной и не обладающей дипольным моментом. Во внешнем электрическом поле обе подрешетки сместятся в противоположных направлениях, т. е. кристалл подвергнется процессу поляризации.
Когда происходит процесс поляризации неоднородного диэлектрика, связанные заряды могут появиться не только на поверхности, но и в объеме диэлектрика. В таком случае электрическое поле E’→ связанных зарядов и полное поле E→ будут обладать сложной структурой, зависящей от геометрии диэлектрика. Утверждение о том, что электрическое поле _formula_ в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем E→ точно верно лишь, когда речь идет об однородном диэлектрике, который заполняет все пространство, где создано внешнее поле. В частности:
В случае, когда в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, напряженность электрического поля E→ этого точечного заряда и потенциал φ в ε раз меньше, чем в вакууме. Запишем данное утверждение в виде формул:
E→=14πε0·Qεr3r→, φ=14πε0Qεr.
Содержание:
Проводники в электрическом поле:
Действие электрического поля распространяется на все без исключения природные объекты — от макроскопических тел до микроскопических частиц, входящих в состав вещества: электроны, протоны, позитроны и т. д. Именно эти частицы определяют электрические свойства различных тел.
Рассмотрим взаимодействие электрического поля с наиболее распространенным классом проводников металлами.
Электрические свойства вещества определяются наличием в них электронов, протонов, ионов.
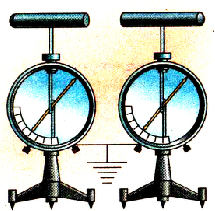
Возьмем два металлических цилиндра и соединим каждый со стержнем заземленного электрометра. Расположим цилиндры между двумя параллельными металлическими пластинами так, чтобы они, касаясь друг друга, составляли единое целое (рис. 1.10). Если зарядим пластины разноименными зарядами, то увидим, что стрелки электрометров отклонятся от положения равновесия и засвидетельствуют наличие заряда на цилиндре (рис. 1.11).
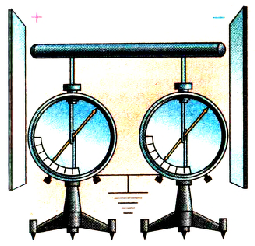 |
Рис. 1.11. Металлические цилиндры в |
Явление возникновения зарядов на проводниках в электрическом поле называется электростатической индукцией.
Если с пластин убрать заряды, то заряды исчезнут и на цилиндрах. Это подтверждает, что на проводнике заряды возникли под действием электрического поля пластин.
Явление возникновения зарядов на проводниках в электрическом поле называется электростатической индукцией.
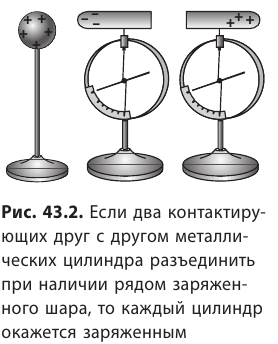
Проведем предыдущий опыт повторно. Но после того как электрометры отметят наличие зарядов на концах проводника, разведем цилиндры и разрядим пластины. Электрометры и после этого будут отмечать наличие зарядов на цилиндрах (рис. 1.11).
Исследовав с помощью эбонитовой палочки знак заряда цилиндра, увидим, что цилиндры имеют разноименные заряды.
Подобное явление наблюдается при электризации всех металлических тел в электрическом поле. Если к металлическому шарику, не заряженному изначально, поднести наэлектризованную эбонитовую или стеклянную палочку, то шарик будет притягиваться к ним. Это можно объяснить тем, что под действием электрического поля заряженной палочки в шарике происходит перераспределение заряженных частиц (рис. 1.12). Поэтому внутри металлических проводников отсутствует электрическое поле. Это явление применяют для изготовления металлических экранов, защищающих различные приборы от действия электрического поля (рис. 1.13).
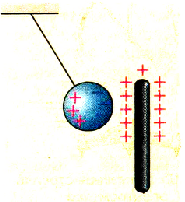 Рис. 1.12. Взаимодействие металлического шарика и заряженной палочки |
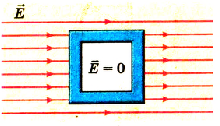
Рис. 1.13. В пространстве, ограниченном |
Металлические экраны устраняют также нежелательное электрическое взаимодействие в различных электронных устройствах.
Проводники и диэлектрики в электрическом поле
Проводя аналогии между гравитационным и электростатическим взаимодействиями, мы находили общие для них свойства. Однако между ними есть и существенные отличия. Одно из них — всепроникаемость гравитационного поля. Действительно, убежище от силы притяжения построить невозможно. А вот от действия сил электростатического поля можно спрятаться достаточно надежно, построив защиту из проводника. Выясним, почему это возможно.
Каковы особенности внутреннего строения проводников
Любое вещество состоит из молекул, атомов или ионов, которые, в свою очередь, содержат заряженные частицы. Поэтому, если вещество поместить в электрическое поле, это вызовет в веществе определенные изменения, зависящие от свойств самого вещества. В зависимости от электрических свойств вещества делят на проводники, диэлектрики, полупроводники.
Проводники — это вещества, способные проводить электрический ток. Любой проводник содержит заряженные частицы, которые могут свободно перемещаться внутри проводника. Типичные представители проводников — металлы. Внутренняя структура металлов представляет собой кристаллическую решетку, образованную положительно заряженными ионами и находящуюся в «газе» свободных электронов. Проводниками также являются электролиты, а при некоторых условиях — и газы. В электролитах свободные заряженные частицы — это положительные и отрицательные ионы, а в газах еще и электроны.
Электростатические свойства проводников
Свойство 1. Напряженность электростатического поля внутри проводника равна нулю.
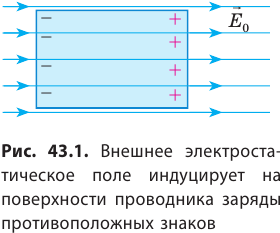
Поместим металлический проводник в электростатическое поле (рис. 43.1). Под действием поля движение свободных электронов станет направленным. Если поле не слишком велико, то электроны не могут оставить провод ник и накапливаются в определенной области его поверхности — эта область приобретает отрицательный заряд, а противоположная область — положительный (его создают оставшиеся там положительные ионы).
Таким образом, на поверхности проводника появляются наведенные (индуцированные) электрические заряды, при этом суммарный заряд проводника остается неизменным (рис. 43.2).
Явление перераспределения электрических зарядов в проводнике, помещенном в электростатическое поле, называют явлением электростатической индукции.
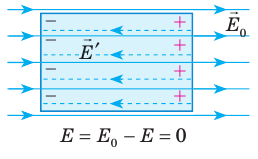
Заряды, индуцированные на поверхности проводника, создают собственное электрическое поле, направленное противоположно внешнему полю (рис. 43.3). Процесс перераспределения зарядов будет продолжаться до момента, когда поле внутри проводника, создаваемое индуцированными зарядами, полностью компенсирует внешнее поле. За очень малый интервал времени напряженность 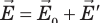
Рис. 43.3. Перераспределение зарядов в проводнике происходит до тех пор, пока модуль напряженности 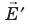
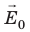
Свойство 2. Поверхность проводника эквипотенциальна. Это утверждение является прямым следствием связи между напряженностью поля и разностью потенциалов: 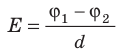
Свойство 3. Весь статический заряд проводника сосредоточен на его поверхности. Данное свойство является следствием закона Кулона и свойства одноименных зарядов отталкиваться.
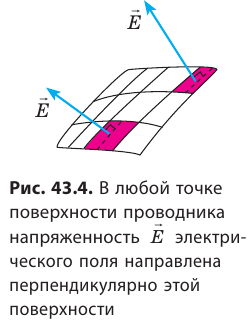
Свойство 4. Вектор напряженности электростатического поля перпендикулярен поверхности проводника (рис. 43.4). Докажем свойство 4 методом от противного.
Предположим, что в определенной точке поверхности проводника вектор 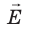
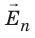
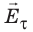
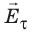
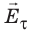
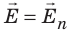
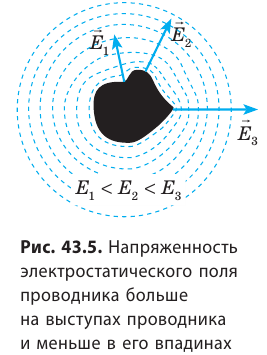
Свойство 5. Электрические заряды распределяются по поверхности проводника так, что напряженность электростатического поля проводника оказывается больше на выступах проводника и меньше в его впадинах (рис. 43.5).
Как применяют электростатические свойства проводников
Приведем примеры использования рассмотренных электростатических свойств проводников.
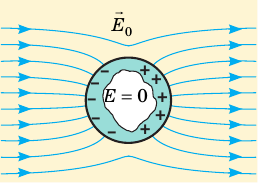
Электростатическая защита. Иногда возникает необходимость изолировать приборы от влияния внешних электрических полей. Очевидно, что для этого их необходимо поместить внутрь металлического корпуса, поскольку внешнее электрическое поле вызывает появление индуцированных зарядов только на поверхности проводника, а поле внутри проводника отсутствует (рис. 43.6). Аналогичный эффект достигается, если сплошную проводящую оболочку заменить металлической сеткой с мелкими ячейками.
Рис. 43.6. Электростатическая защита. Под действием внешнего поля на поверхности металлического корпуса возникают индуцированные заряды, поле которых экранирует внешнее электрическое поле: напряженность поля внутри корпуса становится равной нулю
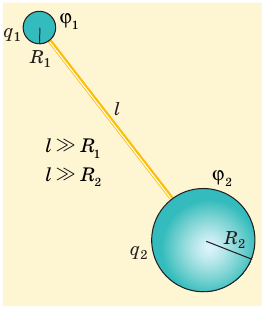
Заземление. Чтобы разрядить небольшое заряженное тело, его необходимо соединить проводником с телом больших размеров: на теле больших размеров накапливается больший электрический заряд. Чтобы обосновать это утверждение, рассмотрим два соединенных проводником проводящих шара радиусами 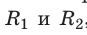
Рис. 43.7. Заряд Q, переданный системе из двух шаров, соединенных проводником, распределится между шарами так, что их потенциалы 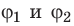
Электрический заряд Q, переданный системе, распределится между шарами таким образом, что их потенциалы будут равными (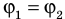
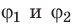
Поскольку 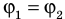
Обратите внимание! Если один из заряженных шаров значительно больше другого, после их соединения практически весь заряд окажется на большем шаре. Этот вывод справедлив и для проводящих тел произвольной формы. Так, если коснуться рукой кондуктора заряженного электроскопа, заряд перераспределится между кондуктором и телом человека, а поскольку человек значительно больше кондуктора, почти весь заряд перейдет на человека.
Часто в качестве тела больших размеров используют весь земной шар: приборы, на которых не должен скапливаться электрический заряд, «заземляют» — присоединяют к массивному проводнику, закопанному в землю.
Каковы особенности внутреннего строения диэлектриков
Диэлектрики — это вещества, плохо проводящие электрический ток: при обычных условиях в них практически нет зарядов, которые могут свободно передвигаться. Обычно выделяют следующие три группы диэлектриков.
| Неполярные диэлектрики | Полярные диэлектрики | Ионные диэлектрики |
|---|---|---|
|
Вещества, молекулы (атомы) которых неполярные: при отсутствии внешнего электростатического поля центры распределения положительных и отрицательных зарядов, из которых состоит молекула (атом), совпадают. Типичными примерами таких веществ являются одноатомные газы; газы, состоящие из симметричных двухатомных молекул; некоторые органические жидкости; пластмассы. |
Вещества, молекулы которых полярные: при отсутствии внешнего электростатического поля центры распределения положительных и отрицательных зарядов в молекуле не совпадают, то есть электронные облака смещены к одному из атомов. Примером полярного диэлектрика является вода ( |
Вещества, имеющие ионную структуру. Среди них — соли и щелочи, например хлорид натрия (NaCl). Кристаллические решетки многих ионных диэлектриков можно рассматривать как состо ящие из двух вставленных друг в друга подрешеток, каждая из которых образована ионами одного знака. При отсутствии внешнего поля каждая ячейка кристалла в целом электронейтральна. |
Как электростатическое поле влияет на диэлектрик
Внесение диэлектрика во внешнее электростатическое поле вызывает поляризацию диэлектрика. В процессе поляризации неполярных диэлектриков проявляется электронный (деформационный) механизм. Под действием внешнего электрического поля молекулы неполярных диэлектриков поляризуются: положительные заряды смещаются в направлении вектора напряженности 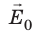
В результате молекулы превращаются в электрические диполи, расположенные вдоль силовых линий внешнего поля. В итоге на поверхностях AB и CD появляются нескомпенсированные связанные заряды противоположных знаков, образующие свое поле, напряженность 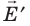
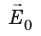
Упорядоченность в расположении молекул вызывает появление на поверхностях AB и CD нескомпенсированных связанных зарядов противоположных знаков. Эти заряды образуют свое поле напряженностью 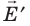
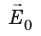
Заметим, что в полярных диэлектриках имеется и электронный механизм поляризации, то есть в результате действия электрического поля происходит смещение зарядов в молекулах. Однако эффект ориентации на несколько порядков превосходит электронный эффект, поэтому последним часто пренебрегают.
При поляризации ионных диэлектриков наблюдается ионная поляризация. Под действием внешнего поля ионы разных знаков, составляющие две подрешетки, смещаются в противоположных направлениях, и в результате на гранях кристалла появляются нескомпенсированные связанные заряды, то есть кристалл поляризуется.
Следует подчеркнуть, что ионная поляризация в чистом виде не наблюдается, — ее всегда сопровождает электронная поляризация.
Как диэлектрик влияет на электростатическое поле
Рассматривая механизмы поляризации диэлектриков, вы узнали, что внесение диэлектрика во внешнее электростатическое поле вызывает появление на его поверхности связанных зарядов. Связанные заряды создают электрическое поле напряженностью 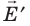
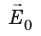
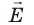
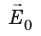
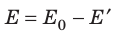
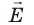
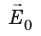
Диэлектрические проницаемости различных веществ могут отличаться в десятки раз. Так, диэлектрическая проницаемость газов близка к единице, жидких и твердых неполярных диэлектриков — к нескольким единицам, полярных диэлектриков — к нескольким десяткам единиц (для воды ε = 81 ). Есть вещества (их называют сегнетоэлектриками), диэлектрическая проницаемость которых составляет значение порядка десятков и сотен тысяч.
Уменьшение напряженности электрического поля в диэлектрике в ε раз по сравнению с напряженностью поля в вакууме приводит к уменьшению силы электростатического взаимодействия. Поэтому закон Кулона для случая взаимодействия двух зарядов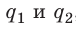
Так же изменяются формулы для определения потенциала ϕ и модуля напряженности E поля, созданного точечным зарядом Q, расположенным в диэлектрике: 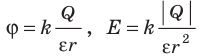
- Диэлектрики в электрическом поле
- Закон Кулона
- Электроемкость
- Полупроводники
- Энергия электрического поля
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
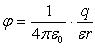
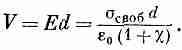
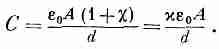
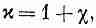
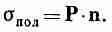
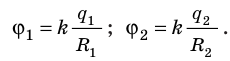
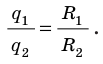
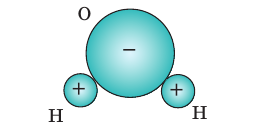
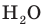 ). Молекулы воды, как и молекулы других полярных диэлектриков, представляют собой микроскопические электрические диполи.
). Молекулы воды, как и молекулы других полярных диэлектриков, представляют собой микроскопические электрические диполи.