Как найти дифференциал матрицы

Любая задача машинного обучения — это задача оптимизации, а задачи оптимизации удобнее всего решать градиентными методами (если это возможно, конечно). Поэтому важно уметь находить производные всего, что попадается под руку. Казалось бы, в чём проблема: ведь дифференцирование — простая и понятная штука (чего не скажешь, например, об интегрировании). Зачем же как-то специально учиться дифференцировать матрицы?

Да в принципе-то никаких проблем: в этой главе вы не узнаете никаких секретных приёмов или впечатляющих теорем. Но, согласитесь, если исходная функция от вектора $x$ имела вид $f(x) = vertvert Ax – bvertvert^2$ (где $A$ — константная матрица, а $b$ — постоянный вектор), то хотелось бы уметь и производную выражать красиво и цельно через буквы $A$, $x$ и $b$, не привлекая отдельные координаты $A_{ij}$, $x_k$ и $b_s$. Это не только эстетически приятно, но и благотворно сказывается на производительности наших вычислений: ведь матричные операции обычно очень эффективно оптимизированы в библиотеках, чего не скажешь о самописных циклах по $i, j, k, s$. И всё, что будет происходить дальше, преследует очень простую цель: научиться вычислять производные в удобном, векторно-матричном виде. А чтобы сделать это и не сойти с ума, мы должны ввести ясную систему обозначений, составляющую ядро техники матричного дифференцирования.

Основные обозначения

Вспомним определение производной для функции $f:mathbb{R}^mrightarrowmathbb{R}^n$. Функция $f(x)$ дифференцируема в точке $x_0$, если

$$f(x_0 + h) = f(x_0) + color{#348FEA}{left[D_{x_0} f right]} (h) + bar{bar{o}} left(left| left| hright|right|right),$$

где $color{#348FEA}{big[D_{x_0} fbig]}$ — дифференциал функции $f$: линейное отображение из мира $x$-ов в мир значений $f$. Грубо говоря, он превращает «малое приращение $h=Delta x$» в «малое приращение $Delta f$» («малые» в том смысле, что на о-малое можно плюнуть):

$$f(x_0 + h) – f(x_0)approxcolor{#348FEA}{left[D_{x_0} f right]} (h)$$

Отметим, что дифференциал зависит от точки $x_0$, в которой он берётся: $color{#348FEA}{left[D_{color{red}{x_0}} f right]} (h)$. Под $vertvert hvertvert$ подразумевается норма вектора $h$, например корень из суммы квадратов координат (обычная евклидова длина).

Давайте рассмотрим несколько примеров и заодно разберёмся, какой вид может принимать выражение $color{#348FEA}{big[D_{x_0} fbig]} (h)$ в зависимости от формы $x$. Начнём со случаев, когда $f$ — скалярная функция.

Примеры конкретных форм $big[D_{x_0} fbig] (h)$, когда $f$ — скалярная функция

1. $f(x)$ — скалярная функция, $x$ — скаляр. Тогда

   $$f(x_0 + h) – f (x_0) approx f'(x_0) (h)$$

   $$color{#348FEA}{left[D_{x_0} fright] (h)} = f'(x_0) h = h cdot f'(x_0)$$

   Здесь $h$ и $f'(x_0)$ — просто числа. В данном случае $color{#348FEA}{left[D_{x_0} fright]}$ — это обычная линейная функция.

2. $f(x)$ — скалярная функция, $x$ — вектор. Тогда

   $$f(x_0 + h) – f(x_0) approx sumlimits_i left.frac{partial f}{partial x_i} right|_{x=x_0} h_i,$$

   то есть

   $$
   color{#348FEA}{left[D_{x_0} fright]}(h) = left(color{#FFC100}{nabla_{x_0} f}right)^T h = langlecolor{#FFC100}{nabla_{x_0} f}, h rangle,
   $$

   где $langlebullet, bulletrangle$ — операция скалярного произведения, а $color{#FFC100}{nabla_{x_0} f} = left(frac{partial f}{partial x_1}, ldots, frac{partial f}{partial x_n}right)$ — градиент функции $f$.

3. $f(x)$ — скалярная функция, $X$ — матрица. Дифференциал скалярной функции по матричному аргументу определяется следующим образом:

   $$
   f(X_0 + H) – f(X_0) approx sumlimits_{i,j} left.frac{partial f}{partial X_{ij}} right|_{X=X_0} H_{ij}
   $$

   Можно заметить, что это стандартное определение дифференциала функции многих переменных для случая, когда переменные — элементы матрицы $X$. Заметим также один интересный факт:

   $$
   sum_{ij} A_{ij} B_{ij} = text{tr}, A^T B,
   $$

   где $A$ и $B$ — произвольные матрицы одинакового размера. Объединяя оба приведённых выше факта, получаем:

   $$
   color{#348FEA}{left[D_{X_0} f right]} (H)
   = sum limits_{ij}
   left.
   frac{partial f}{partial X_{ij}}
   right|_{X = X_0}
   left(
   X – X_0
   right)_{ij}
   = text{tr},
   left( left[left. frac{partial f}{partial X_{ij}}right|_{X=X_0}right]^T Hright).
   $$

   Можно заметить, что здесь, по аналогии с примерами, где $x$ — скаляр и где $x$ — вектор (и $f(x)$ — скалярная функция), получилось на самом деле скалярное произведение градиента функции $f$ по переменным $X_{ij}$ и приращения. Этот градиент мы записали для удобства в виде матрицы с теми же размерами, что матрица $X$.

В примерах выше нам дважды пришлось столкнуться с давним знакомцем из матанализа: градиентом скалярной функции (у нескалярных функций градиента не бывает). Напомним, что градиент $color{#FFC100}{nabla_{x_0} f}$ функции в точке $x_0$ состоит из частных производных этой функции по всем координатам аргумента. При этом его обычно упаковывают в ту же форму, что и сам аргумент: если $x$ — вектор-строка, то и градиент записывается вектор-строкой, а если $x$ — матрица, то и градиент тоже будет матрицей того же размера. Это важно, потому что для осуществления градиентного спуска мы должны уметь прибавлять градиент к точке, в которой он посчитан.

Как мы уже имели возможность убедиться, для градиента скалярной функции $f$ выполнено равенство

$$
left[D_{x_0} f right] (x-x_0) = langlecolor{#FFC100}{nabla_{x_0} f}, x-x_0rangle,
$$

где скалярное произведение — это сумма попарных произведений соответствующих координат (да-да, самое обыкновенное).

Посмотрим теперь, как выглядит дифференцирование для функций, которые на выходе выдают не скаляр, а что-то более сложное.

Примеры конкретных форм $big[D_{x_0} fbig] (h)$, где $f$ — это вектор или матрица

1. $f(x) = begin{pmatrix} f(x_1) vdots f(x_m) end{pmatrix}$, $x$ — вектор. Тогда

   $$
   f(x_0 + h) – f(x_0) =
   begin{pmatrix}
   f(x_{01} + h_1) – f(x_{01})
   vdots
   f(x_{0m} + h_m) – f(x_{0m})
   end{pmatrix}
   approx
   begin{pmatrix}
   f'(x_{01}) h_1
   vdots
   f'(x_{0m}) h_m
   end{pmatrix}
   =
   begin{pmatrix}
   f'(x_{01})
   vdots
   f'(x_{0m})
   end{pmatrix}
   odot
   h.
   $$

   В последнем выражении происходит покомпонентное умножение:

   $$color{#348FEA}{big[D_{x_0} fbig]} (h) = f'(x_0) odot h = h odot f'(x_0)$$

2. $f(X) = XW$, где $X$ и $W$ — матрицы. Тогда

   $$f(X_0 + H) – f(X_0) = (X_0 + H) W – X_0 W = H W,$$

   то есть

   $$color{#348FEA}{big[D_{X_0} fbig]} (H) = H W$$

3. $f(W) = XW$, где $X$ и $W$ — матрицы. Тогда

   $$f(W_0 + H) – f(W_0) = X(W_0 + H) – XW_0 = X H,$$

   то есть

   $$color{#348FEA}{big[D_{W_0} fbig]} (H) = X H$$

4. $f(x) = (f_1(x),ldots,f_K(x))$ — вектор-строка, $x = (x_1,ldots,x_D)$ — вектор-строка. Тогда

   $$
   color{#348FEA}{big[D_{x_0} fbig]}(h)
   = left(sum_j
   left.
   frac{partial f_1}{partial y_j}
   right|_{y=x_0}h_j, ldots, sum_j left. frac{partial f_K}{partial y_j} right|_{y=x_0}h_j right) = \
   = h cdot
   begin{pmatrix}
   left.
   frac{partial f_1}{partial y_1}
   right|_{y=x_0} & ldots &
   left.
   frac{partial f_k}{partial y_1}
   right|_{y=x_0} \
   vdots & & vdots \
   left.
   frac{partial f_1}{partial y_D}
   right|_{y=x_0} & ldots &
   left.
   frac{partial f_k}{partial y_D}
   right|_{y=x_0}\
   end{pmatrix}
   = h cdot
   left.
   frac{partial f}{partial y}right|_{y = x_0}
   $$

   Матрица, выписанная в предпоследней выкладке, — это знакомая вам из курса матанализа матрица Якоби.

Простые примеры и свойства матричного дифференцирования

1. Производная константы. Пусть $f(x) = a$. Тогда

   $$f(x_0 + h) – f(x_0) = 0,$$

   то есть $color{#348FEA}{big[D_{x_0} fbig]}$ — это нулевое отображение. А если $f$ — скалярная функция, то и $color{#FFC100}{nabla_{x_0} f} = 0.$

2. Производная линейного отображения. Пусть $f(x)$ — линейное отображение. Тогда

   $$f(x_0 + h) – f(x_0) = f(x_0) + f(h) – f(x_0) = f(h)$$

   Поскольку справа линейное отображение, то по определению оно и является дифференциалом $color{#348FEA}{big[D_{x_0} fbig]}$. Мы уже видели примеры таких ситуаций выше, когда рассматривали отображения умножения на матрицу слева или справа. Если $f$ — (скалярная) линейная функция, то она представляется в виде $langle a, vrangle$ для некоторого вектора $a$ — он и будет градиентом $f$.

3. Линейность производной. Пусть $f(x) = lambda u(x) + mu v(x)$, где $lambda, mu$ — скаляры, а $u, v$ — некоторые отображения, тогда

   $$color{#348FEA}{big[D_{x_0} fbig]} = lambda color{#348FEA}{big[D_{x_0} ubig]} + mu color{#348FEA}{big[D_{x_0} vbig]}$$

   Попробуйте доказать сами, прежде чем смотреть доказательство.

   $$f(x_0 + h) – f(x_0) = (lambda u(x_0 + h) + mu v(x_0 + h)) – (lambda u(x_0) + mu v(x_0)) =$$

   $$ = lambda(u(x_0 + h) – u(x_0)) + mu(v(x_0 + h) – v(x_0)) approx $$

   $$approx lambda color{#348FEA}{big[D_{x_0} ubig]}(h) + mu color{#348FEA}{big[D_{x_0} vbig]}(h)$$

4. Производная произведения. Пусть $f(x) = u(x) v(x)$, где $u, v$ — некоторые отображения, тогда

   $$color{#348FEA}{big[D_{x_0} fbig]} = color{#348FEA}{big[D_{x_0} ubig]} cdot v(x_0) + u(x_0) cdot color{#348FEA}{big[D_{x_0} vbig]}$$

   Попробуйте доказать сами, прежде чем смотреть доказательство.

   Обозначим для краткости $x = x_0 + h$. Тогда

   $$u(x)v(x) – u(x_0)v(x_0) = u(x)v(x) – u(x_0)v(x) + u(x_0)v(x) – u(x_0)v(x_0) =$$

   $$ (u(x) – u(x_0))v(x) + u(x_0)(v(x) – v(x_0))approx $$

   $$approx color{#348FEA}{big[D_{x_0} ubig]}(h) cdot v(x) + u(x_0)cdot color{#348FEA}{big[D_{x_0} vbig]}(h)$$

   И всё бы хорошо, да в первом слагаемом $v(x)$ вместо $v(x_0)$. Придётся разложить ещё разок:

   $$color{#348FEA}{big[D_{x_0} ubig]}(h) cdot v(x) approx $$

   $$color{#348FEA}{big[D_{x_0} ubig]}(h) cdot left(v(x_0) + color{#348FEA}{big[D_{x_0} vbig]}(h) + o(vertvert hvertvert)right) =$$

   $$color{#348FEA}{big[D_{x_0} ubig]}(h) cdot v(x_0) + bar{bar{o}}left(vertvert hvertvertright)$$

   Это же правило сработает и для скалярного произведения:

   $$color{#348FEA}{big[D_{x_0} langle u, vranglebig]} = langlecolor{#348FEA}{big[D_{x_0} ubig]}, vrangle + langle u, color{#348FEA}{big[D_{x_0} vbig]}rangle$$

   В этом нетрудно убедиться, повторив доказательство или заметив, что в доказательстве мы пользовались лишь дистрибутивностью (= билинейностью) умножения.

5. Производная сложной функции. Пусть $f(x) = u(v(x))$. Тогда

   $$f(x_0 + h) – f(x_0) = u(v(x_0 + h)) – u(v(x_0)) approx $$

   $$approxleft[D_{v(x_0)} u right] (v(x_0 + h) – v(x_0)) approx left[D_{v(x_0)} u right] left( left[D_{x_0} vright] (h)right)$$

   Здесь $D_{v(x_0)} u$ — дифференциал $u$ в точке $v(x_0)$, а $left[D_{v(x_0)} u right]left(ldotsright)$ — это применение отображения $left[D_{v(x_0)} u right]$ к тому, что в скобках. Итого получаем:

   $$left[D_{x_0} color{#5002A7}{u} circ color{#4CB9C0}{v} right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$

6. Важный частный случай: дифференцирование перестановочно с линейным отображением. Пусть $f(x) = L(v(x))$, где $L$ — линейное отображение. Тогда $left[D_{v(x_0)} L right]$ совпадает с самим $L$ и формула упрощается:

   $$left[D_{x_0} color{#5002A7}{L} circ color{#4CB9C0}{v} right](h) = color{#5002A7}{L} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$

Простые примеры вычисления производной

1. Вычислим дифференциал и градиент функции $f(x) = langle a, xrangle$, где $x$ — вектор-столбец, $a$ — постоянный вектор.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Вычислить производную можно непосредственно:

   $$f(x_0 + h) – f(x_0) = langle a, x_0 + hrangle – langle a, x_0rangle = langle a, hrangle$$

   Но можно и воспользоваться формулой дифференциала произведения:

   $$color{#348FEA}{big[D_{x_0} langle a, xranglebig]} (h) = $$

   $$ =langlecolor{#348FEA}{big[D_{x_0} abig]}(h), xrangle + langle a, color{#348FEA}{big[D_{x_0} xbig]}(h)rangle$$

   $$= langle 0, xrangle + langle a, hrangle = langle a, hrangle$$

   Сразу видно, что градиент функции равен $a$.

2. Вычислим производную и градиент $f(x) = langle Ax, xrangle$, где $x$ — вектор-столбец, $A$ — постоянная матрица.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Снова воспользуемся формулой дифференциала произведения:

   $$color{#348FEA}{big[D_{x_0} langle Ax, xranglebig]}(h) = $$

   $$ = langlecolor{#348FEA}{big[D_{x_0} Axbig]}(h), x_0rangle + langle Ax_0, color{#348FEA}{big[D_{x_0} xbig]}(h)rangle$$

   $$= langle Ah, x_0rangle + langle Ax_0, hrangle$$

   Чтобы найти градиент, нам надо это выражение представить в виде $langle ?, hrangle$. Для этого поменяем местами множители первого произведения и перенесём $A$ в другую сторону ($A$ перенесётся с транспонированием):

   $$langle A^Tx_0, hrangle + langle Ax_0, hrangle = $$

   $$= langle (A^T + A)x_0, hrangle$$

   Получается, что градиент в точке $x_0$ равен $(A^T + A)x_0$.

3. Вычислим производную обратной матрицы: $f(X) = X^{-1}$, где $X$ — квадратная матрица.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Рассмотрим равенство $I = Xcdot X^{-1} = I$ и продифференцируем его:

   $$0 = color{#348FEA}{big[D_{X_0} left( Xcdot X^{-1}right)big]}(H) = $$

   $$ = color{#348FEA}{big[D_{X_0} Xbig]}(H)cdot X_0^{-1} + X_0cdot color{#348FEA}{big[D_{X_0} X^{-1}big]}(H)$$

   Отсюда уже легко выражается

   $$color{#348FEA}{big[D_{X_0} X^{-1}big]}(H) = -X_0^{-1}cdotcolor{#348FEA}{big[D_{X_0} Xbig]}(H)cdot X_0^{-1}$$

   Осталось подставить $color{#348FEA}{big[D_{X_0} Xbig]}(H) = H$, но запомните и предыдущую формулу, она нам пригодится.

4. Вычислим градиент определителя: $f(X) = text{det}(X)$, где $X$ — квадратная матрица.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   В предыдущих примерах мы изо всех сил старались не писать матричных элементов, но сейчас, увы, придётся. Градиент функции состоит из её частных производных: $color{#FFC100}{nabla_{x_0} f} = left(frac{partial f}{partial{x_{ij}}}right)_{i,j}$. Попробуем вычислить $frac{partial f}{partial{x_{ij}}}$. Для этого разложим определитель по $i$-й строке:

   $$text{det}(X) = sum_{k}x_{ik}cdot(-1)^{i + k}M_{ik},$$

   где $M_{ik}$ — это определитель подматрицы, полученной из исходной выбрасыванием $i$-й строки и $k$-го столбца. Теперь мы видим, что определитель линеен по переменной $x_{ij}$, причём коэффициент при ней равен $cdot(-1)^{i + k}M_{ik}$. Таким образом,

   $$frac{partial f}{partial{x_{ij}}} = (-1)^{i + k}M_{ik}$$

   Чтобы записать матрицу, составленную из таких определителей, покороче, вспомним, что

   $$X^{-1} = frac1{text{det}(X)}left((-1)^{i+j}M_{color{red}{ji}}right)_{i,j}$$

   Обратите внимание на переставленные индексы $i$ и $j$ (отмечены красным). Но всё равно похоже! Получается, что

   $$color{#FFC100}{nabla_{x_0} f} = text{det}(X)cdot X^{-T},$$

   где $X^{-T}$ — это более короткая запись для $(X^{-1})^T$.

5. Вычислим градиент функции $f(x) = vertvert Ax – bvertvert^2$. С этой функцией мы ещё встретимся, когда будем обсуждать задачу линейной регрессии.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Распишем квадрат модуля в виде скалярного произведения:

   $$vertvert Ax – bvertvert^2 = langle Ax – b, Ax – brangle$$

   Применим формулу дифференциала произведения и воспользуемся симметричностью скалярного произведения:

   $$color{#348FEA}{big[D_{x_0} langle Ax – b, Ax – branglebig]}(h) = $$

   $$ langle color{#348FEA}{big[D_{x_0} (Ax – b)big]}(h), Ax_0 – brangle + langle Ax_0 – b, color{#348FEA}{big[D_{x_0} (Ax – b)big]}(h)rangle$$

   $$ = 2langle Ax_0 – b, color{#348FEA}{big[D_{x_0} (Ax – b)big]}(h)rangle =$$

   $$ = 2langle Ax_0 – b, Ahrangle = langle 2A^T(Ax_0 – b), hrangle$$

   Получаем, что

   $$color{#FFC100}{nabla_{x_0} f} = 2A^T(Ax_0 – b)$$

Примеры вычисления производных сложных функций

1. Вычислим градиент функции $f(X) = text{log}(text{det}(X))$.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Вспомним формулу производной сложной функции:

   $$left[D_{X_0} u circ v right](H) = left[D_{v(X_0)} u right] left( left[D_{X_0} vright] (H)right)$$

   и посмотрим, как её тут можно применить. В роли функции $u$ у нас логарифм:

   $$u(y) = text{log}(u),quad left[D_{y_0} uright](s) = frac1y_0cdot s,$$

   а в роли $v$ — определитель:

   $$v(X) = text{det}(X),quad left[D_{y_0} vright](H) = langle text{det}(X_0)cdot X_0^{-T}, Hrangle,$$

   где под скалярным произведением двух матриц понимается, как обычно,

   $$langle A, Brangle = sum_{i,j}a_{ij}b_{ij} = text{tr}(A^TB)$$

   Подставим это всё в формулу произведения сложной функции:

   $$left[D_{X_0} u circ v right](H) = frac1{text{det}(X)}cdotlangle text{det}(X)cdot X^{-T}, Hrangle =$$

   $$= langle frac1{text{det}(X)}cdottext{det}(X)cdot X^{-T}, Hrangle =
   langle X_0^{-T}, Hrangle$$

   Отсюда сразу видим, что

   $$color{#FFC100}{nabla_{X_0} f} = X_0^{-T}$$

2. Вычислим градиент функции $f(X) = text{tr}(AX^TX)$.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Воспользуемся тем, что след — это линейное отображение (и значит, перестановочно с дифференцированием), а также правилом дифференцирования сложной функции:

   $$left[D_{X_0} f right](H) = text{tr}left(left[D_{X_0} AX^TX right](H)right) =$$

   $$=text{tr}left(Acdotleft[D_{X_0} X^T right](H)cdot X_0 + AX_0^Tleft[D_{X_0} X right](H)right) =$$

   $$=text{tr}left(AH^TX_0 + AX_0^THright)$$

   Чтобы найти градиент, мы должны представить это выражение в виде $langle ?, Hrangle$, что в случае матриц переписывается, как мы уже хорошо знаем, в виде $text{tr}(?^Tcdot H) = text{tr}(?cdot H^T)$. Воспользуемся тем, что под знаком следа можно транспонировать и переставлять множители по циклу:

   $$ldots=text{tr}left(AH^TX_0right) + text{tr}left(AX_0^THright) =$$

   $$=text{tr}left(X_0AH^Tright) + text{tr}left(H^TX_0A^Tright) =$$

   $$=text{tr}left(X_0AH^Tright) + text{tr}left(X_0A^TH^Tright) =$$

   $$=text{tr}left((X_0A + X_0A^T)H^Tright)$$

   Стало быть,

   $$color{#FFC100}{nabla_{X_0} f} = X_0A + X_0A^T$$

3. Вычислим градиент функции $f(X) = text{det}left(AX^{-1}Bright)$.

   Подумайте, кстати, почему мы не можем расписать определитель в виде произведения определителей и тем самым сильно упростить себе жизнь

   Расписать у нас может не получиться из-за того, что $A$ и $B$ могут быть не квадратными, и тогда у них нет определителей и представить исходный определитель в виде произведения невозможно.

   Воспользуемся правилом дифференцирования сложной функции для $u(Y) = text{det}(Y)$, $v(X) = AX^{-1}B$. А для этого сначала вспомним, какие дифференциалы у них самих. С функцией $u$ всё просто:

   $$left[D_{Y_0} uright](S) = langle text{det}(Y_0)Y_0^{-T}, Srangle =$$

   $$= text{tr}left(text{det}(Y_0)Y_0^{-1}Sright)$$

   Функция $v$ сама является сложной, но, к счастью, множители $A$ и $B$ выносятся из-под знака дифференциала, а дифференцировать обратную матрицу мы уже умеем:

   $$left[D_{X_0} vright](H) = – AX_0^{-1}HX_0^{-1} B$$

   С учётом этого получаем:

   $$left[D_{X_0} f right](H) = left[D_{v(X_0)} u right] left( left[D_{X_0} vright] (H)right) =$$

   $$=text{tr}left(text{det}(AX_0^{-1}B)(AX_0^{-1}B)^{-1}left(- AX_0^{-1}HX_0^{-1} Bright)right)$$

   $$=text{tr}left(-text{det}(AX_0^{-1}B)(AX_0^{-1}B)^{-1}AX_0^{-1}HX_0^{-1} Bright)$$

   Чтобы найти градиент, мы должны, как обычно, представить это выражение в виде $text{tr}(?^Tcdot H)$.

   $$ldots=text{tr}left(-text{det}(AX_0^{-1}B)X_0^{-1} B(AX_0^{-1}B)^{-1}AX_0^{-1}Hright)$$

   Стало быть,

   $${nabla_{X_0} f} = left(-text{det}(AX_0^{-1}B)X_0^{-1} B(AX_0^{-1}B)^{-1}AX_0^{-1}right)^T =$$

   $$=-text{det}(AX_0^{-1}B)X_0^{-T} A^T(AX_0^{-1}B)^{-T}B^TX_0^{-T}$$

Вторая производная

Рассмотрим теперь не первые два, а первые три члена ряда Тейлора:

$$f(x_0 + h) = f(x_0) + color{#348FEA}{left[D_{x_0} f right]} (h) + frac12color{#4CB9C0}{left[D_{x_0}^2 f right]} (h, h) + bar{bar{o}} left(left|left| hright|right|^2right),$$

где $color{#4CB9C0}{left[D_{x_0}^2 f right]} (h, h)$ — второй дифференциал, квадратичная форма, в которую мы объединили все члены второй степени.

Вопрос на подумать. Докажите, что второй дифференциал является дифференциалом первого, то есть

$$left[D_{x_0} color{#348FEA}{left[D_{x_0} f right]} (h_1) right] (h_2) = left[D_{x_0}^2 f right] (h_1, h_2)$$

Зависит ли выражение справа от порядка $h_1$ и $h_2$?

Этот факт позволяет вычислять второй дифференциал не с помощью приращений, а повторным дифференцированием производной.

Вторая производная может оказаться полезной при реализации методов второго порядка или же для проверки того, является ли критическая точка (то есть точка, в которой градиент обращается в ноль) точкой минимума или точкой максимума. Напомним, что квадратичная форма $q(h)$ называется положительно определённой (соответственно, отрицательно определённой), если $q(h) geqslant 0$ (соответственно, $q(h) leqslant 0$) для всех $h$, причём $q(h) = 0$ только при $h = 0$.

Теорема. Пусть функция $f:mathbb{R}^mrightarrowmathbb{R}$ имеет непрерывные частные производные второго порядка $frac{partial^2 f}{partial x_ipartial x_j}$ в окрестности точки $x_0$, причём $color{#FFC100}{nabla_{x_0} f} = 0$. Тогда точка $x_0$ является точкой минимума функции, если квадратичная форма $color{#348FEA}{D_{x_0}^2 f} $ положительно определена, и точкой максимума, если она отрицательно определена.

Если мы смогли записать матрицу квадратичной формы второго дифференциала, то мы можем проверить её на положительную или отрицательную определённость с помощью критерия Сильвестра.

Примеры вычисления и использования второй производной

1. Рассмотрим задачу минимизации $f(x) = vertvert Ax – bvertvert^2$ по переменной $x$, где $A$ — матрица с линейно независимыми столбцами. Выше мы уже нашли градиент этой функции; он был равен $color{#FFC100}{nabla_{x_0} f} = 2A^T(Ax – b)$. Мы можем заподозрить, что минимум достигается в точке, где градиент обращается в ноль: $x_* = (A^TA)^{-1}A^Tb$. Отметим, что обратная матрица существует, так как $text{rk}(A^TA) = text{rk}{A}$, а столбцы $A$ по условию линейно независимы и, следовательно, $text{rk}(A^TA)$ равен размеру этой матрицы. Но действительно ли эта точка является точкой минимума? Давайте оставим в стороне другие соображения (например, геометрические, о которых мы упомянем в главе про линейные модели) и проверим аналитически. Для этого мы должны вычислить второй дифференциал функции $f(x) = vertvert Ax – bvertvert^2$.

   Попробуйте вычислить сами, прежде чем смотреть решение.

   Вспомним, что

   $$color{#348FEA}{big[D_{x_0} vertvert Ax – bvertvert^2big]}(h_1) = langle 2A^T(Ax_0 – b), h_1rangle$$

   Продифференцируем снова. Скалярное произведение — это линейная функция, поэтому можно занести дифференцирование внутрь:

   $$color{#348FEA}{big[D_{x_0} langle 2A^T(Ax – b), h_1ranglebig]}(h_2) =
   langle color{#348FEA}{big[D_{x_0} (2A^TAx – 2A^Tb)big]}(h_2), h_1rangle =$$

   $$=langle 2A^TAh_2, h_1rangle = 2h_2^T A^TA h_1$$

   Мы нашли квадратичную форму второго дифференциала; она, оказывается, не зависит от точки (впрочем, логично: исходная функция была второй степени по $x$, так что вторая производная должна быть константой). Чтобы показать, что $x_*$ действительно является точкой минимума, достаточно проверить, что эта квадратичная форма положительно определена.

   Попробуйте сделать это сами, прежде чем смотреть решение.

   Хорошо знакомый с линейной алгеброй читатель сразу скажет, что матрица $A^TA$ положительно определена для матрицы $A$ с линейно независимыми столбцами. Но всё же давайте докажем это явно. Имеем $h^TA^TAh = (Ah)^TAh = vertvert Ahvertvert^2 geqslant 0$. Это выражение равно нулю тогда и только тогда, когда $Ah = 0$. Последнее является однородной системой уравнений на $h$, ранг которой равен числу переменных, так что она имеет лишь нулевое решение $h = 0$.

2. Докажем, что функция $f(X) = log{text{det}(X)}$ является выпуклой вверх на множестве симметричных, положительно определённых матриц. Для этого мы должны проверить, что в любой точке квадратичная форма её дифференциала отрицательно определена. Для начала вычислим эту квадратичную форму.

   Попробуйте сделать это сами, прежде чем смотреть решение.

   Выше мы уже нашли дифференциал этой функции:

   $$color{#348FEA}{big[D_{X_0} log{text{det}(X)}big]}(H_1) = langle X_0^{-T}, H_1rangle$$

   Продифференцируем снова:

   $$color{#348FEA}{big[D_{X_0} langle X^{-T}, H_1ranglebig]}(H_2) =
   langle color{#348FEA}{big[D_{x_0} X^{-T}big]}(H_2), h_1rangle =$$

   $$=langle -X_0^{-1}H_2X_0^{-1}, H_1rangle$$

   Чтобы доказать требуемое в условии, мы должны проверить следующее: что для любой симметричной матрицы $X_0$ и для любого симметричного (чтобы не выйти из пространства симметричных матриц) приращения $Hne 0$ имеем

   $$color{#348FEA}{big[D^2_{X_0} log{text{det}(X)}big]}(H, H) < 0$$

   Покажем это явно. Так как $X_0$ — симметричная, положительно определённая матрица, у неё есть симметричный и положительно определённый квадратный корень: $X_0 = X_0^{1/2}cdot X_0^{1/2} = X_0^{1/2}cdot left(X_0^{1/2}right)^T.$ Тогда

   $$langle -X_0^{-1}HX_0^{-1}, Hrangle = -text{tr}left(X_0^{1/2} left(X_0^{1/2}right)^THX_0^{1/2} left(X_0^{1/2}right)^TH^Tright) =$$

   $$-text{tr}left(left(X_0^{1/2}right)^THX_0^{1/2} left(X_0^{1/2}right)^TH^TX_0^{1/2}right) = $$

   $$=-text{tr}left( left(X_0^{1/2}right)^THX_0^{1/2} left[left(X_0^{1/2}right)^THX_0^{1/2}right]^Tright) =$$

   $$=-vertvertleft(X_0^{1/2}right)^THX_0^{1/2}vertvert^2,$$

   что, конечно, меньше нуля для любой ненулевой $H$.

Обновление: 8 января 2020
Обновление: 16 февраля 2020

Вместо введения

С момента прошлой заметки по данной теме прошло много времени, но интерес к изложенному в ней не утихал. Разобравшись с основной проблемой (как, собственно, реализовать дифференцирование) читатели стали задавать вопросы о двух приведённых в тексте формулах. На этих формулах построен весь вывод, но сами они не выводятся, а сопровождены комментарием о простоте их получения при должной внимательности. Настало время.

Замечание о качестве

Мне никогда не попадался вывод этих формул. Обычно, если у вас проблемы с матрицей, то надо обращаться либо к Нео, либо к Гантмахеру    [?]

Ф.Р. Гантмахер “ТЕОРИЯ МАТРИЦ”

. Но в этот раз – мне никто не помог. Так что, не обессудьте: вывел как умею.

Технология

Подобные формулы (“Нагромождение из матриц” – “знак равенства” – “некоторая функция от матриц”) выводятся стандартно: вы опускаетесь на уровень ниже – до компонент объектов (разбирая что там “под капотом” происходит), аккуратно (я бы даже сказал “осторожно”) проделываете все преобразования с позиции компонент, получаете некий, более-менее конечный, результат и поднимаетесь на уровень выше (пытаясь интерпретировать формулы из компонент с позиции исходных объектов).

Первая формула

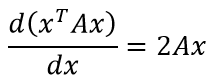
Отмечу, что это частный случай для симметричной матрицы A. В более же общем случае, формула имеет вид:

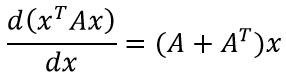
Для того, чтобы выражение в скобках можно было вычислить, необходимо, чтобы объекты имели следующие размеры:

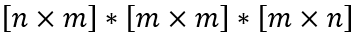
Так как x – вектор, то min(m,n) = 1.

Зададимся конкретикой: пусть x – вектор-столбец, тогда n=1.

Объекты, таким образом, будут иметь вид:

Теперь, наконец-то, можно приступить к выводу. Здесь главное ничего не потерять, поэтому сперва аккуратно проделаем умножение x^TA, а затем домножим результат на x.

Ожидаемо, мы получаем скаляр, зависящий от вектора. Возьмём производную скалярной функции от векторного аргумента:

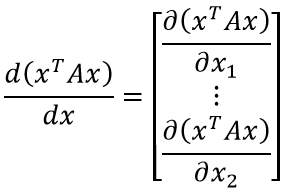
Чтобы получить данное выражение, необходимо найти общий вид производной по k-ой компоненте вектора. Попробуем сгруппировать слагаемые дифференцируемого выражения по компонентам вектора, опираясь на выражение для x^TAx, полученное ранее:

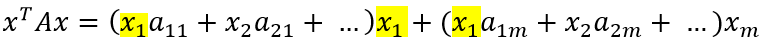
Очевидно, что раскрытие первых скобок даст нам x₁ в квадрате с множителем a₁₁ плюс сумму произведений x₁ со всеми остальными слагаемыми внутри первых скобок. Также, x₁ входит в остальные скобки по одному разу, что образует ещё слагаемые вида x₁*a_…*x_….

Таким образом:

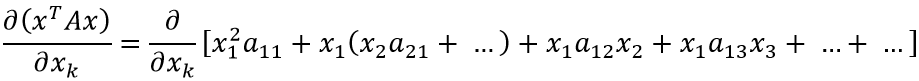
Если присмотреться, можно заметить закономерность (приведены множители x_k: оставшаяся часть выражения скрыта за многоточием):

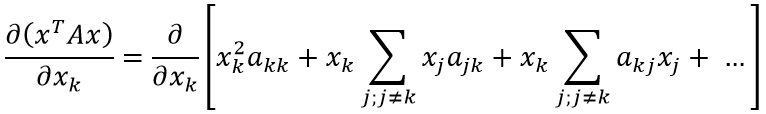
Теперь найти производную не составит труда:

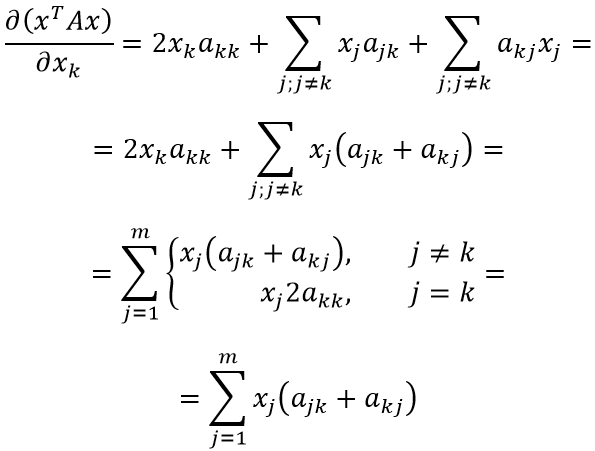
В преобразованиях выше мы сначала объединили две сумму в одну (т.к. индексы, по которым идёт суммирование совпадают), затем первое слагаемое внесли как частный случай суммы под знак суммирования (в соответствии с индексом при x). Последняя операция изменяет условия суммирования: теперь сумма определена для всех возможных значений индекса j.

Наконец, можно заметить, что (a_jk+a_kj) при выполнении j=k соответствует (a_kk+a_kk) = 2a_kk. Таким образом, выражение для первого условия покрывает и выражение для второго условия – сумму можно переписать без ветвления. Для всех компонент вектора x формула коэффициента оказалась одинакова.

Теперь несложно продолжить дифференцирование:

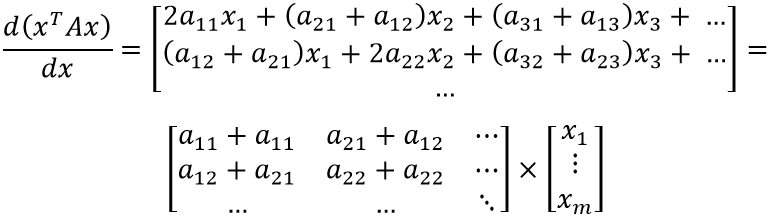
Осталось заметить, что левый множитель представляет собой специфическое суммирование элементов матрицы. Несложно догадаться, что компонент jk складывается с kj при сложении матрицы с её транспонированным вариантом:

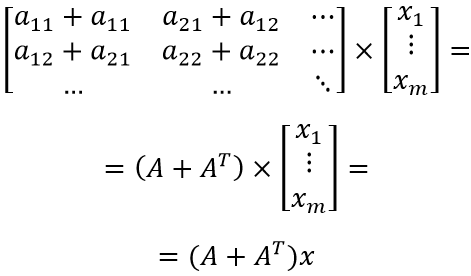
Оставляя начальное и конечное выражения, получаем:

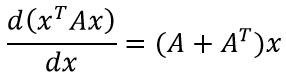
ЧТД

Вторая формула

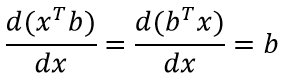
Формула (особенно, по сравнению с предыдущей) достаточна проста для восприятия и объясняется “на пальцах”. x^Tb и b^Tx – это просто сумма попарного произведения компонент двух векторов (первый вектор приходится транспонировать для существования соответствующего матричного произведения). Ну и, не менее очевидное – скорость изменения от x каждой компоненты результирующего вектора определяется соответствующей компонентой вектора b.

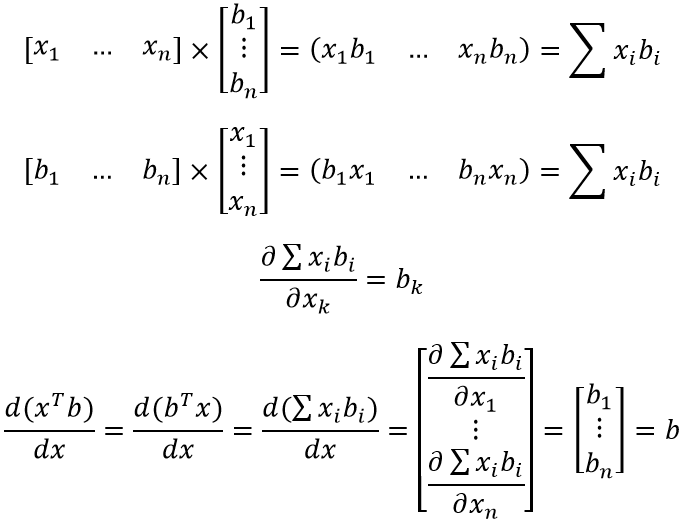
ЧТД

Вместо выводов

Производные скалярной, векторной и матричной функций по векторному аргументу

Рассмотрим скалярную (числовую) функцию нескольких переменных . Упорядоченный набор переменных будем называть векторным аргументом этой функции и обозначать . Первый дифференциал функции имеет вид:

Сумму в правой части можно представить как произведение строки на столбец , либо как произведение строки на столбец .

Матрица-строка или матрица-столбец определяют производную скалярной функции по векторному аргументу (градиент скалярной функции). Двойственность определения относится только к форме записи, поскольку векторный аргумент функции можно считать столбцом (в этом случае дифференциал — столбец) или понимать как строку. В любом случае для первого дифференциала получаем одно и то же выражение (6.1).

Второй дифференциал функции имеет вид

Обозначим через матрицу частных производных второго порядка (матрицу Гессе). Тогда правую часть (6.2) можно записать в виде произведения

---

Замечания 6.1

1. Для записи производных можно использовать символические векторы (столбцы или строки):

При этом дифференцирование функции формально записывается как умножение функции на символический вектор производных. Например, градиент функции есть произведение вектора на функцию , а матрица Гессе есть произведение символической матрицы

на функцию .

2. Определитель матрицы Гессе называется гессианом.

3. Свойства градиента функции и матрицы Гессе используются в методах поиска экстремума функции.

---

Пример 6.2. Найти первую и вторую производные сложной функции , применяя матричные обозначения.

Решение. Находим производные функции , заменяя суммирование операциями умножения соответствующих матриц:

Сравним матричную форму записи этих производных с производными в случае скалярной функции

Выражения для первой производной совпадают, а для второй производной -отличаются незначительно, причем полное совпадение будет, если учесть, что для скалярной величины .

---

Производные векторной функции по векторному аргументу

Пусть задан столбец функций нескольких переменных (говорят, что задана вектор-функция векторного аргумента). Первый дифференциал вектор-функции имеет вид:

Обозначим через матрицу частных производных первого порядка заданных функций (матрицу Якоби). Тогда выражение для первого дифференциала можно записать в виде , т.е. — производная вектор-функции векторного аргумента.

Как и в случае с аргументом , упорядоченный набор функций можно считать не матрицей-столбцом, а матрицей-строкой . Этот случай сводится к предыдущему, учитывая, что операции дифференцирования и транспонирования можно выполнять в любом порядке, так как (здесь и далее аргумент для упрощения записи опущен). Поэтому из равенства получаем

, где

— транспонированная матрица Якоби вектор-функции .

Заметим, что из равенства следует правило транспонирования производных вектор-функции: .

---

Правила дифференцирования по векторному аргументу

Векторный аргумент , его приращение считаем матрицами-столбцами размеров .

1. Первый дифференциал скалярной функции имеет вид:

где — градиент функции, а .

2. Второй дифференциал скалярной функции имеет вид

где — матрица Гессе.

3. Первый дифференциал вектор-функции {матрицы-столбца) имеет вид:

, где — матрица Якоби.

Первый дифференциал матрицы-строки: .

4. В частном случае, когда , получаем

, где — единичная матрица n-го порядка.

5. Числовую матрицу (соответствующих размеров) можно выносить за знак производной:

Последняя формула следует из правила транспонирования производных:

6. Производные суммы, разности и произведения вектор-функций и одинаковых размеров

Докажем, например, последнее равенство. Найдем частную производную скалярной функции по переменной

Тогда первый дифференциал функции имеет вид

Запишем это выражение, используя матричные обозначения

Сравнивая полученное выражение с , приходим к равенству , что и требовалось доказать.

7. Производная сложной функции , где и вычисляется по формуле:

или, опуская аргументы, .

Действительно, запишем первый дифференциал вектор-функции: . Заметим, что матрицы Якоби в правой части формулы согласованы: матрица имеет размеры , матрица . Найдем, используя обычные правила дифференцирования, частную производную . В правой части стоит произведение i-й строки матрицы на j-й столбец матрицы , что и требовалось показать.

Использование матричных обозначений позволяет записывать и применять правила дифференцирования по векторному аргументу аналогично правилам дифференцирования в скалярном случае. Например, правило 7 дифференцирования сложной вектор-функции формально совпадает с обычным “цепным” правилом дифференцирования скалярной сложной функции одной переменной. Разумеется, что формальное совпадение правил становится фактическим в скалярном случае, когда все матрицы имеют размеры .

---

Пример 6.3. Применяя правила дифференцирования по векторному аргументу, найти производные следующих функций:

а) ; б) ; в) ; г) ; д) ,

где — квадратная числовая матрица n-го порядка; — столбцы размеров , причем столбец числовой.

Решение. а) Вынося постоянный множитель (матрицу-строку) по правилу 5 и учитывая правило 4, получаем:

б) Учитывая, что величина скалярная, т.е. , получаем . Заметим, что .

в) По правилам 4 и 5 находим: .

г) По правилам 4 и 5 находим: .

д) Представляя скалярное выражение как произведение строки на столбец , по правилу 6 (где ) получаем

с учетом правила транспонирования производных

Учитывая результат п. “б”, имеем .

---

Замечания 6.2

1. В некоторых областях прикладной математики, например, в методах оптимизации и теории управления, часто используются другие соглашения, совпадающие с изложенными с точностью до операции транспонирования. Производная (градиент функции ) считается матрицей-столбцом, а производная — матрицей-строкой:

Тогда соответствующие формулы дифференцирования, аналогичные полученным в примере 6.3, имеют вид:

2. Если матрица Якоби квадратная , то ее определитель называется якобианом.

3. След матрицы Якоби (при ) определяет

дивергенцию вектор-функции векторного аргумента .

---

Производные матричной функции по векторному аргументу

Рассмотрим функциональную матрицу , элементами которой служат функции векторного аргумента . Дифференциал этой функции имеет вид

где — частная производная матрицы по одной переменной. Совокупность частных производных (градиент функциональной матрицы) представляет объект, элементы которого нумеруются тремя индексами: номер строки, номер столбца и номер переменной дифференцирования. Поэтому заменить операцию суммирования в правой части формулы операцией умножения матриц в данном случае не представляется возможным. Необходимо вводить другие объекты — тензоры и операции над ними. Поясним формальную сторону получения удобных формул дифференцирования на примере функциональных матриц. Примем следующие правила индексирования:

1) элементы матрицы обозначаются , где — номер строки, а — номер столбца. В частности, — матрица-столбец (или просто столбец), а — матрица-строка (или просто строка);

2) частную производную функции (скалярной, векторной или матричной) по переменной будем обозначать, приписывая нижний индекс в скобках: ;

3) если в произведении одинаковые индексы встречаются сверху и снизу, то по ним производится суммирование (хотя знак суммы не указывается). Например, если — матрица размеров , — столбец размеров , — строка размеров , то

т.е. — i-й элемент столбца , — j-й элемент строки , — число .

Применяя эти соглашения, запишем дифференциалы:

— скалярной функции: ;

— вектор-функции (функции-столбца): ;

— функциональной матрицы , где — частная производная первого порядка элемента функциональной матрицы по переменной .

Одним из преимуществ принятых соглашений является получение простого вида формул. Другие преимущества раскрываются и используются в тензорном анализе.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

From Wikipedia, the free encyclopedia

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders. A matrix differential equation contains more than one function stacked into vector form with a matrix relating the functions to their derivatives.

For example, a first-order matrix ordinary differential equation is

where is an vector of functions of an underlying variable , is the vector of first derivatives of these functions, and is an matrix of coefficients.

In the case where is constant and has n linearly independent eigenvectors, this differential equation has the following general solution,

where λ₁, λ₂, …, λ_n are the eigenvalues of A; u₁, u₂, …, u_n are the respective eigenvectors of A; and c₁, c₂, …, c_n are constants.

More generally, if commutes with its integral then the Magnus expansion reduces to leading order, and the general solution to the differential equation is

where is an constant vector.

By use of the Cayley–Hamilton theorem and Vandermonde-type matrices, this formal matrix exponential solution may be reduced to a simple form.^[1] Below, this solution is displayed in terms of Putzer’s algorithm.^[2]

Stability and steady state of the matrix system[edit]

The matrix equation

with n×1 parameter constant vector b is stable if and only if all eigenvalues of the constant matrix A have a negative real part.

The steady state x* to which it converges if stable is found by setting

thus yielding

assuming A is invertible.

Thus, the original equation can be written in the homogeneous form in terms of deviations from the steady state,

An equivalent way of expressing this is that x* is a particular solution to the inhomogeneous equation, while all solutions are in the form

with a solution to the homogeneous equation (b=0).

Stability of the two-state-variable case[edit]

In the n = 2 case (with two state variables), the stability conditions that the two eigenvalues of the transition matrix A each have a negative real part are equivalent to the conditions that the trace of A be negative and its determinant be positive.

Solution in matrix form[edit]

The formal solution of has the matrix exponential form

evaluated using any of a multitude of techniques.

Putzer Algorithm for computing e^At[edit]

Given a matrix A with eigenvalues ,

where

The equations for are simple first order inhomogeneous ODEs.

Note the algorithm does not require that the matrix A be diagonalizable and bypasses complexities of the Jordan canonical forms normally utilized.

Deconstructed example of a matrix ordinary differential equation[edit]

A first-order homogeneous matrix ordinary differential equation in two functions x(t) and y(t), when taken out of matrix form, has the following form:

where , , , and may be any arbitrary scalars.

Higher order matrix ODE’s may possess a much more complicated form.

Solving deconstructed matrix ordinary differential equations[edit]

The process of solving the above equations and finding the required functions of this particular order and form consists of 3 main steps. Brief descriptions of each of these steps are listed below:

• Finding the eigenvalues
• Finding the eigenvectors
• Finding the needed functions

The final, third, step in solving these sorts of ordinary differential equations is usually done by means of plugging in the values calculated in the two previous steps into a specialized general form equation, mentioned later in this article.

Solved example of a matrix ODE[edit]

To solve a matrix ODE according to the three steps detailed above, using simple matrices in the process, let us find, say, a function x and a function y both in terms of the single independent variable t, in the following homogeneous linear differential equation of the first order,

To solve this particular ordinary differential equation system, at some point in the solution process, we shall need a set of two initial values (corresponding to the two state variables at the starting point). In this case, let us pick x(0) = y(0) = 1.

First step[edit]

The first step, already mentioned above, is finding the eigenvalues of A in

The derivative notation x′ etc. seen in one of the vectors above is known as Lagrange’s notation (first introduced by Joseph Louis Lagrange. It is equivalent to the derivative notation dx/dt used in the previous equation, known as Leibniz’s notation, honoring the name of Gottfried Leibniz.)

Once the coefficients of the two variables have been written in the matrix form A displayed above, one may evaluate the eigenvalues. To that end, one finds the determinant of the matrix that is formed when an identity matrix, , multiplied by some constant λ, is subtracted from the above coefficient matrix to yield the characteristic polynomial of it,

and solve for its zeroes.

Applying further simplification and basic rules of matrix addition yields

Applying the rules of finding the determinant of a single 2×2 matrix, yields the following elementary quadratic equation,

which may be reduced further to get a simpler version of the above,

Now finding the two roots, and of the given quadratic equation by applying the factorization method yields

The values and , calculated above are the required eigenvalues of A.
In some cases, say other matrix ODE’s, the eigenvalues may be complex, in which case the following step of the solving process, as well as the final form and the solution, may dramatically change.

Second step[edit]

As mentioned above, this step involves finding the eigenvectors of A from the information originally provided.

For each of the eigenvalues calculated, we have an individual eigenvector. For the first eigenvalue, which is , we have

Simplifying the above expression by applying basic matrix multiplication rules yields

All of these calculations have been done only to obtain the last expression, which in our case is α = 2β. Now taking some arbitrary value, presumably, a small insignificant value, which is much easier to work with, for either α or β (in most cases, it does not really matter), we substitute it into α = 2β. Doing so produces a simple vector, which is the required eigenvector for this particular eigenvalue. In our case, we pick α = 2, which, in turn determines that β = 1 and, using the standard vector notation, our vector looks like

Performing the same operation using the second eigenvalue we calculated, which is , we obtain our second eigenvector. The process of working out this vector is not shown, but the final result is

Third step[edit]

This final step finds the required functions that are ‘hidden’ behind the derivatives given to us originally. There are two functions, because our differential equations deal with two variables.

The equation which involves all the pieces of information that we have previously found, has the following form:

Substituting the values of eigenvalues and eigenvectors yields

Applying further simplification,

Simplifying further and writing the equations for functions x and y separately,

The above equations are, in fact, the general functions sought, but they are in their general form (with unspecified values of A and B), whilst we want to actually find their exact forms and solutions. So now we consider the problem’s given initial conditions (the problem including given initial conditions is the so-called initial value problem). Suppose we are given , which plays the role of starting point for our ordinary differential equation; application of these conditions specifies the constants, A and B. As we see from the conditions, when t = 0, the left sides of the above equations equal 1. Thus we may construct the following system of linear equations,

Solving these equations, we find that both constants A and B equal 1/3. Therefore substituting these values into the general form of these two functions
specifies their exact forms,

the two functions sought.

Using matrix exponentiation[edit]

The above problem could have been solved with a direct application of the matrix exponential. That is, we can say that

Given that (which can be computed using any suitable tool, such as MATLAB’s expm tool, or by performing matrix diagonalisation and leveraging the property that the matrix exponential of a diagonal matrix is the same as element-wise exponentiation of its elements)

the final result is

This is the same as the eigenvector approach shown before.

See also[edit]

• Nonhomogeneous equations
• Matrix difference equation
• Newton’s law of cooling
• Fibonacci sequence
• Difference equation
• Wave equation
• Autonomous system (mathematics)

References[edit]