Как найти дифференциал параметрически заданной функции

Рассмотрим вопрос о дифференцировании функций, заданных параметрическим путем. До этого мы имели дело с функциями вида y=f(x)y=f(x) (то есть с явной зависимостью) и неявными функциями F(x,y)=0F(x, y)=0. Однако это не единственные способы представления функциональной зависимости между двумя величинами yy и xx.

Речь идет о функциях, которые задаются неким параметром tt. Идея состоит в том, что мы рассматриваем две «обычные» функции x=φ(t)x=varphi (t) и y=ψ(t)y=psi (t). Здесь видно, что каждому значению аргумента (параметра) tt будут отвечать какие-то частные значения функций φ(t)varphi (t) и ψ(t)psi (t). То есть для каждого значения tt мы получим два значения: xx и yy. А теперь смотрите: мы можем забыть, что у нас есть параметр tt, а довольствоваться только парой величин xx и yy.

Можно увидеть здесь функциональную зависимость между xx и yy и даже попытаться представить эту зависимость в привычном нам виде y=f(x)y=f(x). Следующие примеры помогут уяснить эту идею.

Примеры параметрически заданных функций

Пример 1

x=φ(t)=tx=varphi (t)=t,

y=ψ(t)=t2y=psi (t)=t^2

Это элементарный пример. Функция φ(t)varphi (t) имеет обратную, и мы легко можем выразить tt через xx. Здесь эти функции попросту совпадают и t=xt=x. Подставим теперь это выражение в функцию y=ψ(t)y=psi (t):

y=ψ(t)=t2=x2y=psi (t)=t^2=x^2

Вот мы и получили обычную функцию y=f(x)=x2y=f(x)=x^2. Дифференцировать такие функции мы, конечно, умеем. Здесь это просто f′(x)=2xf'(x)=2x.

Пример 2

x=φ(t)=t4x=varphi (t)=t^4,

y=ψ(t)=sin⁡ty=psi (t)=sin t

Чтобы представить данную функцию в обычном виде, нам нужно избавится от tt. То есть выразить его из одной функции и подставить в другую. В нашем случае tt проще выразить из первой функции. Получаем t=x14t=x^{frac{1}{4}}. Теперь подставим это в функцию для yy:

y=sin⁡t=sin⁡(x14)y=sin t=sin big({x^{frac{1}{4}}}big)

Пример 3

x=φ(t)=a(t−sin⁡t)x=varphi (t)=a(t-sin t),

y=ψ(t)=a(1−cos⁡t)y=psi (t)=a(1-cos t),

−∞<t<∞-infty<t<infty

Если мы начертим кривую, задаваемую этими уравнениями (функциями), то получим удивительное изображение циклоиды. Ранее мы имели дело с такими параметрически заданными функциями, где без труда можно было избавиться от tt. Но бывают случаи, когда это сделать довольно непросто, а порой даже невозможно. В таком случае мы не сможем записать нашу функцию в виде y=f(x)y=f(x) и взять производную по тем правилам, которые мы уже знаем. Этот пример, впрочем, позволяет исключить tt. Можно пытаться выразить tt через yy из второго уравнения. Получается что-то вроде арккосинуса. Подставив tt в первое уравнение, мы получим функцию зависимости xx от yy. Но, возможно, нам захочется получить функцию yy от аргумента xx, а с этим могут возникнуть проблемы. А потом нужно будет это еще продифференцировать.

Так что все выглядит не очень просто. К счастью, математики на этот счет придумали способ, как можно вычислить производную от yy по xx, не получая предварительно функциональной зависимости вида y=f(x)y=f(x). Этим мы сейчас и займемся.

Дифференцирование параметрически заданной функции

Итак, представим себе, что xx и yy заданы как функции некого параметра tt:

x=φ(t)x=varphi (t),

y=ψ(t)y=psi (t).

Предположим также, что функции φ(t)varphi (t) и ψ(t)psi (t) нужное число раз дифференцируемые, то есть имеют нужное число производных по аргументу (параметру) tt. Наложим еще одно условие: чтобы у функции x=φ(t)x=varphi (t) существовала обратная функция t=φ−1(x)t=varphi^{-1}(x). Это значит, что первая производная φ′(t)varphi ‘(t) отлична от нуля.

Найдем теперь первую производную от yy по xx. Как вы помните, из определения производной следует, что:

yx′=dydx.y’_x=frac{dy}{dx}.

Запишем теперь аналогично первые производные от функций φ(t)varphi (t) и ψ(t)psi (t) по tt:

x′(t)=φ′(t)=dxdt,x'(t)=varphi ‘(t)=frac{dx}{dt},

y′(t)=ψ′(t)=dydt.y'(t)=psi ‘(t)=frac{dy}{dt}.

Теперь выразим дифференциалы dxdx и dydy: dx=φ′(t)dtdx=varphi ‘(t)dt и dy=ψ′(t)dtdy=psi ‘(t)dt. Наконец, подставим их в определение первой производной функции y(x)y(x):

yx′=dydx=ψ′(t)dtφ′(t)dt=ψ′(t)φ′(t).y’_x=frac{dy}{dx}=frac{psi ‘(t)dt}{varphi ‘(t)dt}=frac{psi ‘(t)}{varphi ‘(t)}.

Вот это и есть главное правило дифференцирования параметрически заданных функций. Сформулируем его так:

Если нам даны функции x=φ(t)x=varphi (t) и y=ψ(t)y=psi (t) параметра tt, то производная от функции yy по аргументу xx представляется выше приведенной формулой. Нужно просто производную ψ′(t)psi ‘(t) разделить на производную φ′(t)varphi ‘(t).

Теперь, кстати, понятно, почему мы потребовали, чтобы первая производная φ′(t)varphi ‘(t) была отлична от нуля. В противном случае у нас в знаменателе оказался бы нуль, а на нуль, как известно, делить очень трудно. Аналогичным образом можно подойти и к определению формул для производных функции y=f(x)y=f(x) высших порядков.

Теперь, вооружившись этой главной формулой, мы можем приступить к тем примерам, которые мы приводили раньше. Для двух первых случаев мы вычислим производные yx′y’_x двумя способами и сравним их. То есть сначала мы используем правило дифференцирования параметрически заданных функций, а потом воспользуемся явным видом функции y=f(x)y=f(x) там, где это возможно сделать.

Пример 1

x=φ(t)=tx=varphi (t)=t,

y=ψ(t)=t2y=psi (t)=t^2

x′(t)=φ′(t)=1x'(t)=varphi ‘(t)=1

y′(t)=ψ′(t)=2ty'(t)=psi’ (t)=2t

yx′=ψ′(t)φ′(t)=2ty’_x=frac{psi’ (t)}{varphi ‘(t)}=2t

Для того чтобы получить эту производную как функцию xx, а не tt, нам нужно выразить tt через xx и подставить в формулу для производной. Вы можете сказать, зачем нам нужен этот новый способ дифференцирования параметрически заданных функций, если нам все равно приходится выражать tt через xx. Но здесь это нужно сделать только для того, чтобы получить результат дифференцирования, то есть производную, как функцию xx. Саму же производную (пусть даже параметра tt) мы получили без какого бы то ни было выражения tt через xx. И уж точно мы не пытались записать функцию вида y=f(x)y=f(x). Так что разница все-таки есть.

Хорошо, tt легко выражается через xx: t=xt=x. Значит: yx′=2t=2xy’_x=2t=2x.

Вычислим теперь эту производную, воспользовавшись явной функцией f(x)f(x). Раннее мы установили, что y=x2y=x^2 и f′(x)=2xf'(x)=2x. Это совпадение и доказывает, что мы все делаем правильно.

Пример 2

x=φ(t)=t4x=varphi (t)=t^4,

y=ψ(t)=sin⁡ty=psi (t)=sin t

t=x14t=x^{frac{1}{4}}

y=sin⁡t=sin⁡(x14)y=sin t=sin big({x^{frac{1}{4}}}big)

x′(t)=φ′(t)=4t3x'(t)=varphi ‘(t)=4t^3

y′(t)=ψ′(t)=cos⁡ty'(t)=psi’ (t)=cos t

yx′=ψ′(t)φ′(t)=14cos⁡tt3y’_x=frac{psi’ (t)}{varphi ‘(t)}=frac{1}{4}frac{cos t}{t^3}

Подставим теперь сюда tt как функцию xx:

yx′=14cos⁡(x14)x34y’_x=frac{1}{4}frac{cos big(x^{frac{1}{4}}big)}{x^frac{3}{4}}

Теперь вычислим производную y′(x)y'(x) прямо:

y′(x)=ddxsin⁡(x14)=cos⁡(x14)ddxx14=14cos⁡(x14)x34y'(x)=frac{d}{dx}sin big({x^{frac{1}{4}}}big)=cos (x^frac{1}{4})frac{d}{dx}x^{frac{1}{4}}=frac{1}{4}frac{cos big(x^frac{1}{4}big)}{x^frac{3}{4}}

Отлично, опять совпадение.

Пример 3

x=φ(t)=a(t−sin⁡t)x=varphi (t)=a(t-sin t),

y=ψ(t)=a(1−cos⁡t)y=psi (t)=a(1-cos t),

−∞<t<∞-infty<t<infty

Здесь мы вычислим производную только первым способом.

x′(t)=φ′(t)=a(1−cos⁡t)x'(t)=varphi ‘(t)=a(1-cos t)

y′(t)=ψ′(t)=asin⁡ty'(t)=psi’ (t)=asin t

yx′=asin⁡ta(1−cos⁡t)=ctg⁡t2,     t≠2πk,  k∈Zy’_x=frac{asin t}{a(1-cos t)}=ctg frac{t}{2}, tneq 2pi k, k in Z

Если

,
то производная имеет вид

.

Доказательство.

.

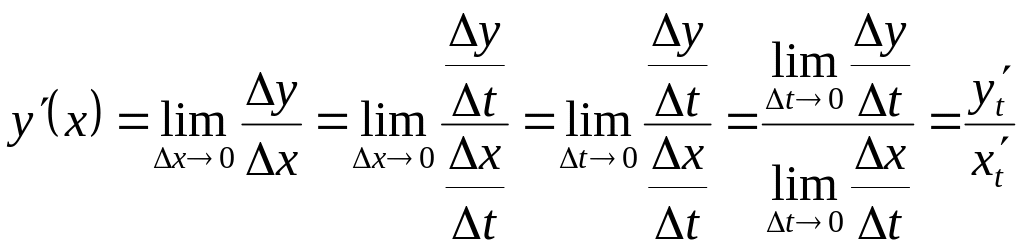
Пример.

,

,

,

.

Примеры для
самостоятельного решения

Определить

7.21.

,
7.22.

7.23.

.

§ 7.6. Первый дифференциал функции, инвариантность его формы

Как уже говорилось
выше,

.

Теорема.
Форма записи дифференциала (первого
дифференциала) функции не отличается
для случаев независимой и зависимой
переменной, то есть инвариантна.

Доказательство.
Пусть

– сложная функция, причем

независимая
переменная,

зависящая
от

переменная. В соответствии с только что
введенной формулой для дифференциала
имеем

,
но

является сложной функцией и при вычислении
производной это следует учесть. Поскольку

,

,
а подчеркнутые члены представляют собой
дифференциал функции

,
естественно, можно записать

.
Итак, дифференциал функции можно
представить двумя формулами

и

,
причем

независимая,
а

зависимая
переменные. Нетрудно заметить, что форма
записи дифференциала одинакова, то есть
инвариантна.

Это свойство
первого дифференциала функции лежит в
основе интегрирования.

Пример.

,  

.

§ 7.7. Производные и дифференциалы высших порядков

В математике широко
используются производные функции высших
порядков. Это оправдывается хотя бы
тем, что физический смысл второй
производной представляет собой ускорение
тела. В самом деле, если вторую производную
функции ввести как производную от
производной, то есть

,

и учесть, что
физический смысл первой производной
есть скорость, то вторая производная,
очевидно, показывает скорость изменения
этой скорости, то есть ускорение.

Аналогично можно
ввести понятия третьей, четвертой и так
далее производных:

,

…..

За редким исключением
производные высших порядков вычисляются
последовательно, то есть для получения
пятой производной необходимо вначале
найти первую, затем вторую, третью и
четвертую производные, и после этого
пятую производную.

Пример 1.

,

,

,

…

На примере 1 было
показано, как находить старшие производные
для явно
заданной
функции.

Пример 2. Вычислим
вторую производную неявной
функции

Определим вначале
первую производную, дифференцируя обе
части равенства по

,

или

.

Дифференцируем
полученное уравнение еще раз

,

тогда

.

После приведения
подобных членов

определяем

.

Из полученного
выражения можно исключить первую
производную, которую определим из ранее
полученного уравнения

,
после приведения подобных членов

тогда

.

Примеры для
самостоятельного решения

Вычислить

7.24.

,
7.25.

.

Определим вторую
производную для параметрически
заданной
функции, для чего выведем необходимую
для этого формулу. Ранее была получена
формула для первой производной функции

,
которая имела вид

.
Дифференцируем обе части равенства по

,
тогда

.

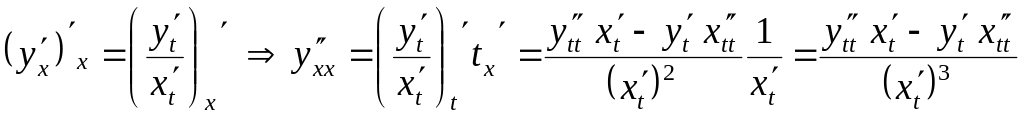
Итак,

.

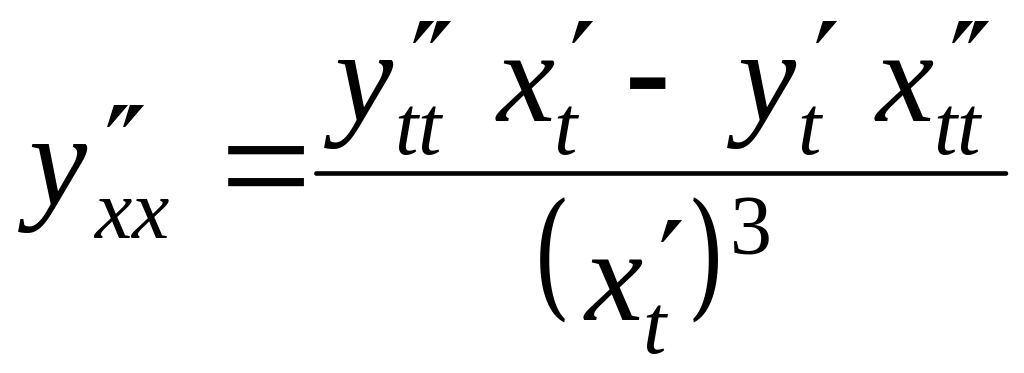
Пример. Дана
функция

.
Определить

.

В соответствии с
полученной формулой находим

,

,

,

,

Очевидно,

.

Примеры для
самостоятельного решения

Вычислить

7.26.

, 7.27.

,
7.28.

.

Дифференциалы
высших порядков

По аналогии с
производными введем понятие дифференциала
второго порядка, обозначив его

:

.

Этот дифференциал
не обладает инвариантностью формы
записи. Покажем это. Очевидно,

.

Если функция

простая, то есть,

независимая
переменная, то аргумент

и его приращение

никак не связаны между собой, другими
словами

может быть любым числом из области
существования функции

тоже, следовательно,

при дифференцировании по

ведет себя как постоянная тогда

.

Когда функция
сложная

,
имеется связь между ее промежуточным
аргументом

и его приращением

поскольку и

,
и

зависят от

.
В выражении для производной, а
следовательно, и дифференциала появляется
второе слагаемое

.

Еще больше
дополнительных членов появляется в
третьем дифференциале сложной функции
и так далее.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Макеты страниц

Простое объяснение принципов решения дифференцирования параметрической функции и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.