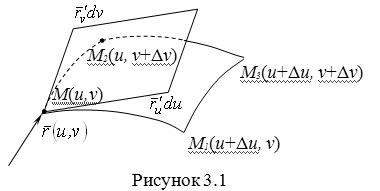
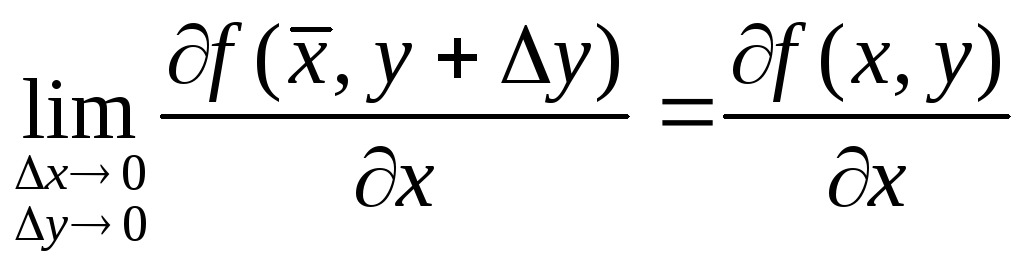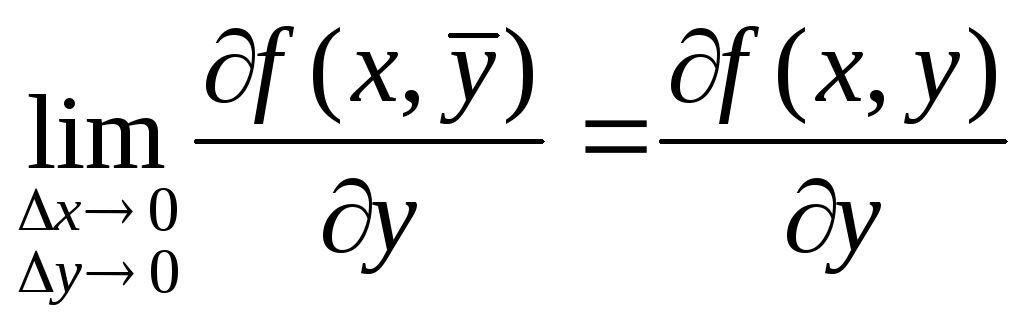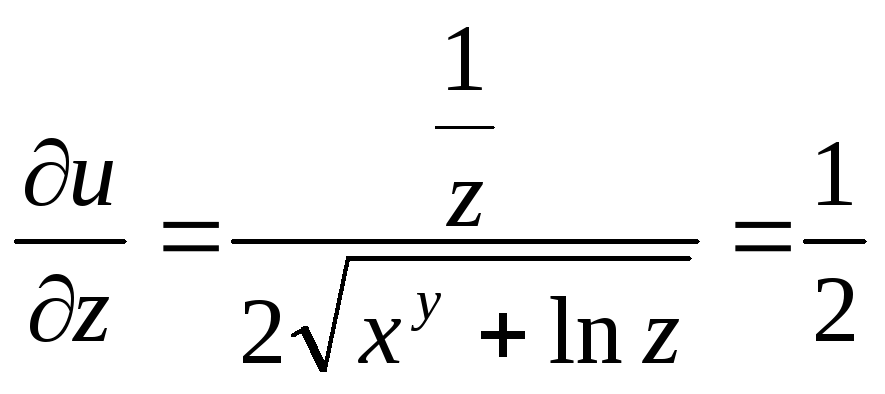Рассмотрим координатную сеть линий на поверхности и криволинейный четырёхугольник, образованный линиями с постоянными значениями координат U И U+DU, V И V+DV, пересекающимися в точках (рис. 3.1). Выделяя главные части приращений
И приближенно (при малых ) заменяя криволинейный четырёхугольник параллелограммом, построенным на векторах
и
, как показано на рис. 2.1, запишем площадь параллелограмма в виде
.
С учётом формулы (3.7) находим
. (3.11)
Поскольку криволинейный четырёхугольник мало отличается от параллелограмма при , величину
называют Дифференциалом площади поверхности
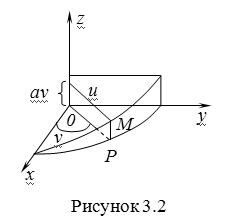
Пример 1. Геликоид. Эта поверхность получается при винтовом движении отрезка прямой, параллельного плоскости и пересекающего ось
(ось винтового движения). Проекция отрезка прямой на плоскость
равномерно вращается около начала координат, а точка пересечения с осью
равномерно перемещается по этой оси (рис. 3.2).
Запишем вектора
,
,
,
Тогда ,
,
, линейный элемент
.
Координатные линии здесь записываются таким образом:
– линия – винтовая линия; при полном обороте (на угол 2P) проекции
точка М поднимается на 2PА, где А – шаг винта;
– линия во всех точках имеет одну и ту же аппликату
; проекция линии на плоскость
Определяется уравнением
.
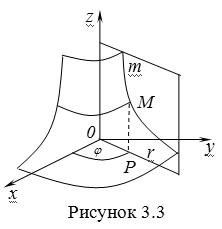
,
Где Z И R – прямоугольные декартовы координаты в этой плоскости, причем ось Or лежит на пересечении этой плоскости с плоскостью XOY. Пусть теперь M вращается вокруг оси Oz. Вводя на плоскости XOY полярные координаты R,J , получаем для точки P (проекции точки M, лежащей на линии M) следующие координаты, которые при вращении линии будут изменяться вместе с углом вращения j
.
Точка М имеет эти две координаты и ещё третью координату
.
Таким образом, радиус-вектор произвольной точки, лежащей на поверхности вращения, имеет вид
,
,
,
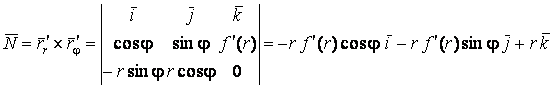
Тогда
,
,
,
Линейный элемент
.
Так как , то координатные линии образуют ортогональную сеть. Линии j=Const Называются меридианами (они получаются в сечении поверхности плоскостями, проходящими через ось вращения). Линии R=const называются параллелями (они получаются в сечении поверхности плоскостями, перпендикулярными оси Oz), это окружности с центрами на оси Oz.
| < Предыдущая | Следующая > |
|---|
Формула Стокса дает возможность перейти от интеграла по поверхности к интегралу по границе поверхности, и наоборот. Важно, чтобы обход контура согласовался с выбранной стороной поверхности (внутрь или наружу).
Наведем формулу Стокса
Дальше в примерах будем использовать компактную запись формулы через определитель.
В целом, поверхностные и криволинейные интегралы достаточно трудно вычислять, на это идет много времени как на практических так и при самостоятельных расчетах.
Пример 1 Используя формулу Стокса, вычислить интеграл
где С- круг x2+y2+z2=a2, x+y+z=0, что пробегается против хода часовой стрелки, если смотреть с положительной стороны оси Ox.
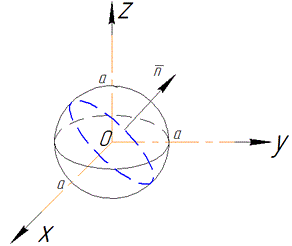
Решение: Криволинейный интеграл второго рода возведем к поверхностному интегралу первого рода, используя формулу Стокса :
здесь нужно подставить свои функции, которые берем из подынтегральной
P=P(x, y, z) =y, P=P(x, y, z) =z, P=P(x, y, z) =x.
Пройдемся по алгоритму вычисления интеграла, чтобы Вы видели, что за чем нужно делать.
Сначала нужно найти дифференциал ds и направляющие косинусы поверхности, которую ограничивает фигура:
из уравнения сферы x2+y2+z2=a2 выражаем z(x, y)
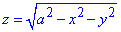
Вычисляем частичные производные
и подставляем в формулу дифференциала поверхности
Найдем направляющие косинусы заданной поверхности:
Поскольку сфера x2+y2+z2=a2 пересекается плоскостью x+y+z=0, то нормальный вектор плоскости равен:
тогда норма вектора
Можем записать направляющие косинусы
Вычислим заданный криволинейный интеграл 2-го рода по формуле Стокса :
При интегрировании перешли к полярной СК. Поскольку имеем кратный интеграл, то умножили на якобиан перехода, дальше расставили пределы и проинтегрировали.
Формула интегрирования, возможно, неудобная для пересмотра на мобильных, но при желании многие из Вас смогут разобраться с интегралом.
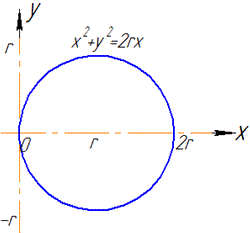
Пример 2 Используя формулу Стокса, вычислить интеграл
где C – кривая x2+y2+z2=2rx, x2+y2=2rx (0<r<R, z>0), какая пробегается так, что ограниченная ей наименьшая область на внешней стороне сферы остается слева.
Решение: Повторно наведем формулу возведения криволинейный интеграла второго рода к поверхностному интегралу первого рода с помощью формулы Стокса:
Выпишем подынтегральные функции
P=P(x, y, z)=y2+z2, Q=Q(x, y, z)=x2+z2, R=R(x, y, z)=x2+y2.
Выполняем расчеты для нахождения дифференциала dS но направляющих косинусам поверхности:
из уравнения x2+y2+z2=2rx получим
Берем частичные производные первого порядка по “икс, игрек”
Вычисляем дифференциал
Найдем направляющие косинусы поверхности за формулами:
Перед радикалами берем знак “-“, поскольку нормаль поверхности образует острый угол с осью Oz.
Заранее вычислим определитель, который стоит под знаком поверхностного интеграла:
Криволинейный интеграл второго рода вычисляем по формуле Стокса:
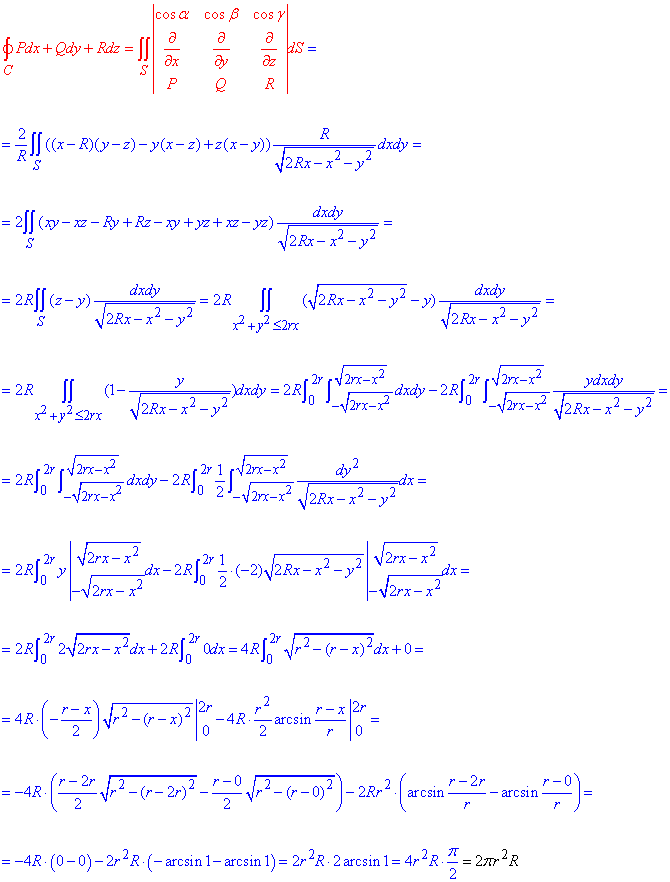
Конечное значение компактное, однако, чтобы его получить пришлось использовать не один листок А4.
Если есть желание можете распечатать формулу и детальнее проанализировать двойной интеграл.
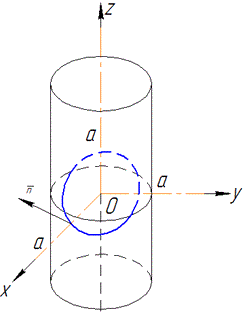
Пример 3 Используя формулу Стокса, вычислить интеграл
где C – эллипс x2+y2=a2, x/a+z/h=1 (a>0, h>0), что пробегается против хода часовой стрелки, если смотреть с положительной стороны оси Ox.
Решение: Интеграл 2-го рода сведём к поверхностному интегралу первого рода за формулой Стокса:
Выписываем функции P=P(x, y, z)=y-z, P=P(x, y, z)=z-x, P=P(x, y, z) =x-y.
Превращаем второе уравнение x/a+z/h=1, чтобы выразить “зет”
Тогда производная равна
Видим, что получили функцию независимую от координаты “игрек”, поэтому производная по ней равна нулю.
Помните об этом когда придет время искать дифференциал поверхности
Поразмышляем как найти направляющие косинусы к поверхности:
Поскольку цилиндр x2+y2=a2 пересечен плоскостью x/a+z/h=1, то нормальный вектор плоскости равен:
Подумайте, почему именно так!
Вычисляем модуль нормали
и необходимые для интегрирования косинусы
За формулой Стокса находим криволинейный интеграл второго рода:
В конце расчетов использовали формулу площади круга с радиусом R=a
Если сможете повторить самостоятельно вычисления на подобных примерах, и правильно найдете интегралы, то Вы на хорошем уровне выучили интегрирование!
ПОВЕРХНОСТИ
Поверхность может быть задана одним уравнением
|
|
(l) |
или
|
|
(ll) |
а также в параметрическом виде тремя уравнениями
|
|
(lll) |
где α, β – параметры. Эти уравнения можно заменить одним векторным уравнением
|
|
(lV) |
где – радиус-вектор точки поверхности.
Линия на поверхности, заданной параметрически, дается этими же уравнениями, если α и β – функции одного параметра. Линии α=const, β=const образуют на поверхности сеть криволинейных координат. Квадрат дифференциала ds длины дуги линии на поверхности можно представить в виде
где
– коэффициенты Гаусса.
Выражение Edα2+2Fdαdβ+Gdβ2 называется первой квадратичной формой поверхности.
Если поверхность задана уравнением (I) или (II), то уравнение касательной плоскости соответственно будет
или
Если же поверхность задана уравнениями (III) или уравнением (IV), то уравнение касательной плоскости
где М (х, у, z) – точка касания; X, Y, Z – текущие координаты касательной плоскости.
Уравнение нормали к поверхности, заданной уравнением (I), имеет вид
Дифференциал площади поверхности dσ определяется по формуле
Пусть поверхность задана уравнением (IV), а ,
– единичные векторы (орты), касательные к линиям α(β=const), β(α=const) и направленные в стороны возрастания параметров α, β, (
,
совпадают по направлению с векторами
,
). Обозначим через
единичный вектор нормали к поверхности, направленный в каждой ее точке так, что орты
,
,
образуют правую систему.
Рассмотрим какую-либо линию L1, проведенную на поверхности через ее точку M1. Пусть К – кривизна линии в точке M1, а – единичный вектор главной нормали к этой линии в точке М1 направленный в сторону вогнутости линии. Проекция вектора кривизны Kv на направление вектора
в точке М1 называется нормальной кривизной линии L1 в точке М1. Линия на поверхности, у которой в каждой точке нормальная кривизна равна нулю, называется асимптотической линией.
Если через точку М1 поверхности провести нормальное сечение (плоскостью, проходящей через нормаль к поверхности в точке M1), то получится плоская линия, у которой в точке M1 вектор главной нормали совпадает с вектором
или противоположен ему. Поэтому кривизна нормального сечения совпадает или отличается только знаком от нормальной кривизны Kn этого сечения. Величина Kn определяется по формуле
где
Выражение Ldα2 + 2Mdαdβ+Ndβ2 называется второй квадратичной формой поверхности. Знак величины Кn определяется знаком второй квадратичной формы (поскольку первая квадратичная форма равна ds2 и, следовательно, положительна).
Центр кривизны наклонного сечения поверхности совпадает с проекцией на его плоскость центра кривизны нормального сечения, имеющего общую касательную с наклонным сечением. Если R – радиус кривизны нормального сечения, то радиус кривизны ρ наклонного сечения можно определить из равенства ρ=RcosX( ,
), где
– единичный вектор главной нормали линии, образованной наклонным сечением, a
– единичный вектор нормали к поверхности (
и
берутся в той точке поверхности, через которую проведены оба сечения).
Среди всевозможных нормальных сечений поверхности, проходящих через ее точку М, имеются два сечения, образованных взаимно перпендикулярными плоскостями, для которых Кn принимает наибольшее и наименьшее значения. Эти два сечения называются главными нормальными сечениями, а соответствующие им значения Кn называются главными кривизнами поверхности и обозначаются K1, К2. Величины R1=1/K1, R2=1/К2 называются главными радиусами кривизны поверхности. Величины К1, К2 находятся как корни квадратного уравнения
Направления касательных к главным нормальным сечениям поверхности называются главными направлениями на поверхности. Линия на поверхности, в каждой точке которой касательная имеет главное направление, называется линией кривизны. Через каждую точку поверхности проходят две взаимно ортогональные линии кривизны. Поэтому удобно выбирать криволинейные координаты α, β так, чтобы линии α, β были бы линиями кривизны. Величины
называется средней и гауссовой (полной) кривизнами поверхности.
Точка поверхности, в которой K1 и К2 имеют одинаковые знаки (К>0) называется эллиптической; в этой точке LN-М2>0. В более частном случае, когда в точке поверхности К1=К2, эта точка называется омбилической, а когда K1=K2=0 – точкой уплощения. Точка поверхности, в которой K1 и К2 имеют разные знаки (К<0), называется гиперболической; в этой точке LN-М2<0. Точка, в которой одна из величин К1, К2 равна нулю (К=0), называется параболической: в ней LN-M2=0.
Через каждую точку поверхности в любом направлении проходит геодезическая линия, которая определяется тем, что в каждой ее точке главная нормаль этой линии совпадает с нормалью к поверхности. Геодезическая линия на поверхности обладает свойством прямой линии на плоскости: из всевозможных линий на поверхности, проходящих через две произвольные точки, кратчайшую дугу, соединяющую эти точки, имеет геодезическая линия.
Многие строительные конструкции имеют очертания поверхностей вращения или поверхностей переноса.
Поверхность вращения образуется вращением плоской линии (образующей или меридиана) вокруг оси. Линия пересечения поверхности вращения с плоскостью, перпендикулярной оси вращения, есть окружность, называемая параллелью. Пусть ось вращения принята за координатную ось Z. Если меридиан, расположенный в плоскости XOZ, задан уравнениями х=х(α), z=z(α), где α – длина дуги меридиана, отсчитываемая от выбранной начальной точки, то сама поверхность вращения определяется уравнениями x=R(α) cos β, у=R(α) sin β, z=z(α). В этих уравнениях: R(α)=x(α) – радиус параллели, проходящей через точку М (х, у, z) данной поверхности, а β – угол между плоскостью XOZ и плоскостью, проходящей через ось Z и точку М. Когда поверхность вращения задана указанными уравнениями, имеем
Поверхностью переноса называется поверхность, описываемая линией (производящей), которая перемещается в пространстве, оставаясь параллельной самой себе (два положения линии называются параллельными, если одно из них получается из другого в результате смещения каждой точки линии на один и тот же вектор – вектор переноса). При перемещении производящей любая ее фиксированная точка М0 вычерчивает линию. Поэтому можно считать, что производящая, перемещаясь в пространстве, опирается своей точкой М0 на некоторую линию, называемую направляющей.
Пусть
– векторные уравнения соответственно производящей и направляющей поверхности переноса. Тогда уравнение самой поверхности переноса с точностью до постоянного вектора будет
или в другом виде
где х(α, β)=аx(α)+bх(β), у(α, β)=ау(α)+bу(β); z(α, β)=аz(α)+bz(β).
Поделитесь ссылкой в социальных сетях
У этого термина существуют и другие значения, см. Дифференциал.
Дифференциа́л (от лат. differentia — разность, различие) в математике — линейная часть приращения дифференцируемой функции или отображения.
Это понятие тесно связано с понятием производной по направлению.
Обозначения[править | править код]
Обычно дифференциал 

Некоторые авторы предпочитают обозначать 
Дифференциал в точке 


![{displaystyle df[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/339506a1d3af2b8c0875a7074fc00c4a3831278f)
(

Если 






}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2b1937707f54e8225b90ea280fc6cc6d86e2148)
Используется так же обозначение 
последнее связано с тем, что дифференциал
является естественным поднятием 


Определения[править | править код]
Для вещественнозначных функций[править | править код]
Пусть 
гладкая функция.
Дифференциал 


где 



Для отображений гладких многообразий[править | править код]
Дифференциал гладкого отображения из гладкого многообразия в многообразие 


где 








Это понятие естественным образом обобщает понятия дифференциала функции.
Связанные определения[править | править код]
Свойства[править | править код]
Примеры[править | править код]
- где
есть матрица Якоби отображения
в точке
.
См. также[править | править код]
- Кодифференциал
Производные и дифференциалы функций нескольких переменных
Определение.
Пусть в некоторой области задана функция
z
= f(x,
y).
Возьмем произвольную точку М(х, у) и
зададим приращение Dх
к переменной х. Тогда величина Dxz
= f(
x
+ Dx,
y)
– f(x,
y)
называется частным
приращением функции по х.
Можно
записать
.
Тогда
называетсячастной
производной функции
z
= f(x,
y)
по х.
Обозначение:
Аналогично
определяется частная производная
функции по у.
Геометрическим
смыслом частной
производной (допустим
)
является тангенс угла наклона касательной,
проведенной в точкеN0(x0,
y0,
z0)
к сечению поверхности плоскостью у =
у0.
Полное приращение и полный дифференциал
Определение.
Для функции f(x,
y)
выражение Dz
= f(
x
+ Dx,
y
+ Dy)
– f(x,
y)
называется полным
приращением.
Если
функция f(x,
y)
имеет непрерывные частные производные,
то
Применим
теорему Лагранжа к выражениям, стоящим
в квадратных скобках.
здесь
Тогда
получаем
Т.к.
частные производные непрерывны, то
можно записать равенства:
Определение.
Выражение
называетсяполным
приращением функции
f(x,
y)
в некоторой точке (х, у), где a1
и a2
– бесконечно малые функции при Dх
®
0 и Dу
®
0 соответственно.
Определение:
Полным
дифференциалом функции
z
= f(x,
y)
называется главная линейная относительно
Dх
и Dу
приращения функции Dz
в точке (х, у).
Для
функции произвольного числа переменных:
Пример.
Найти полный дифференциал функции
.
Пример.
Найти полный дифференциал функции
Геометрический смысл полного дифференциала Касательная плоскость и нормаль к поверхности

N
j
N0
касательная
плоскость
Пусть N
и N0
– точки данной поверхности. Проведем
прямую NN0.
Плоскость, которая проходит через точку
N0,
называется касательной
плоскостью
к поверхности, если угол между секущей
NN0
и этой плоскостью стремится к нулю,
когда стремится к нулю расстояние NN0.
Определение.
Нормалью к
поверхности в точке N0
называется прямая, проходящая через
точку N0
перпендикулярно касательной плоскости
к этой поверхности.
В
какой – либо точке поверхность имеет,
либо только одну касательную плоскость,
либо не имеет ее вовсе.
Если
поверхность задана уравнением z
= f(x,
y),
где f(x,
y)
– функция, дифференцируемая в точке
М0(х0,
у0),
касательная плоскость в точке
N0(x0,y0,(x0,y0))
существует и имеет уравнение:
.
Уравнение
нормали к поверхности в этой точке:
Геометрическим
смыслом
полного дифференциала функции двух
переменных f(x,
y)
в точке (х0,
у0)
является приращение аппликаты (координаты
z)
касательной плоскости к поверхности
при переходе от точки (х0,
у0)
к точке (х0+Dх,
у0+Dу).
Как
видно, геометрический смысл полного
дифференциала функции двух переменных
является пространственным аналогом
геометрического смысла дифференциала
функции одной переменной.
Пример.
Найти уравнения касательной плоскости
и нормали к поверхности
в
точке М(1, 1, 1).
Уравнение
касательной плоскости:
Уравнение
нормали:
Приближенные вычисления с помощью полного дифференциала
Пусть
функция f(x,
y)
дифференцируема в точке (х, у). Найдем
полное приращение этой функции:
Если
подставить в эту формулу выражение
то
получим приближенную формулу:
Пример.
Вычислить приближенно значение
,
исходя из значения функцииприx
= 1, y
= 2, z
= 1.
Из
заданного выражения определим Dx
= 1,04 – 1 = 0,04, Dy
= 1,99 – 2 = -0,01,
Dz
= 1,02 – 1 = 0,02.
Найдем
значение функции u(x,
y,
z)
=
Находим
частные производные:
Полный
дифференциал функции u
равен:
Точное
значение этого выражения: 1,049275225687319176.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
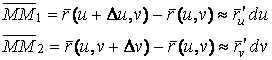

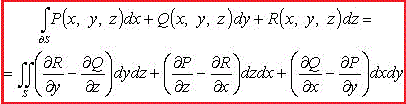
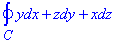
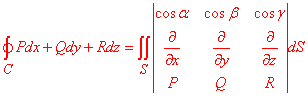
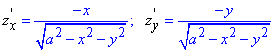
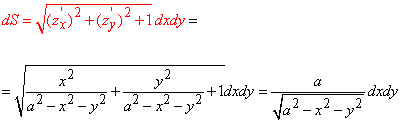
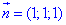
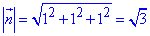
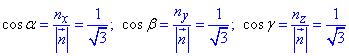
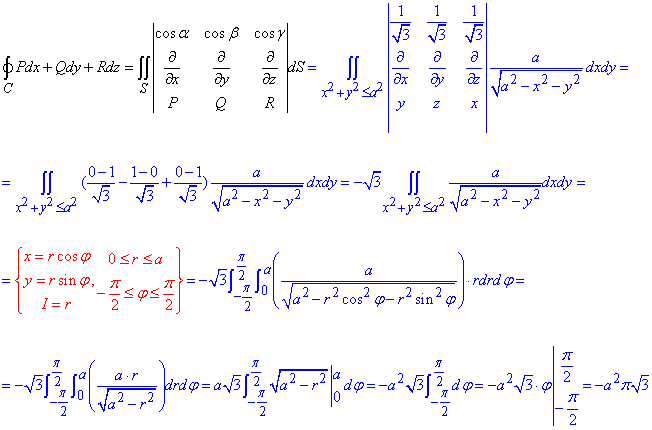
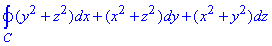
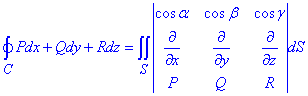
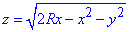
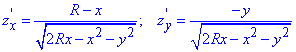
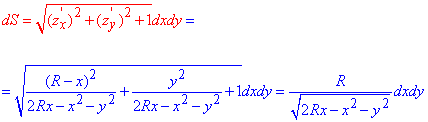
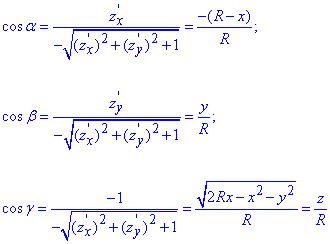
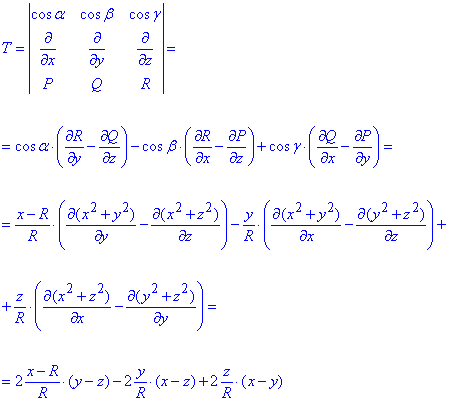
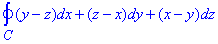
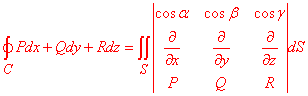
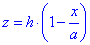
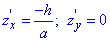
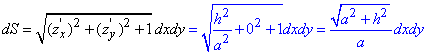
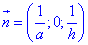
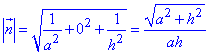
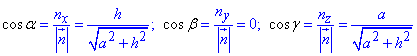
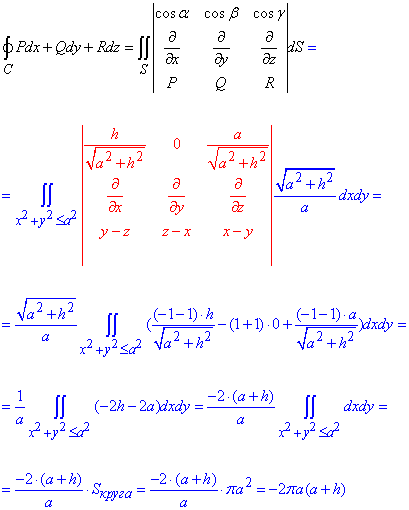



![{displaystyle [dF(X)]g=X(gcirc F),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c45ba685ed05609da38126b814c5c651c6e9032)