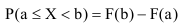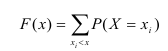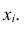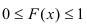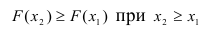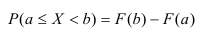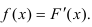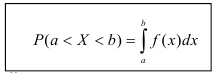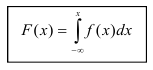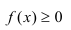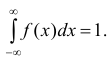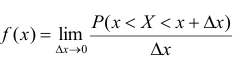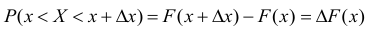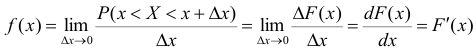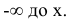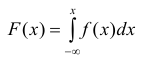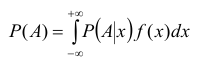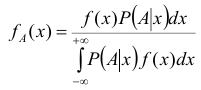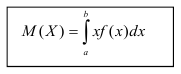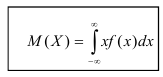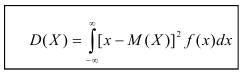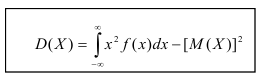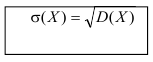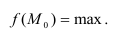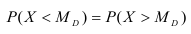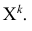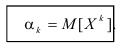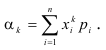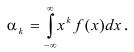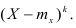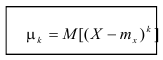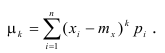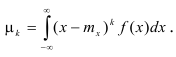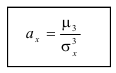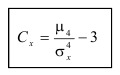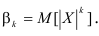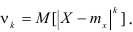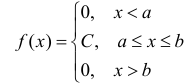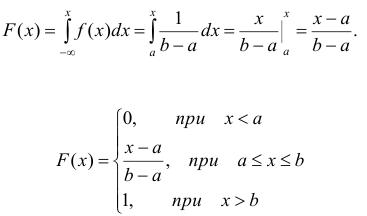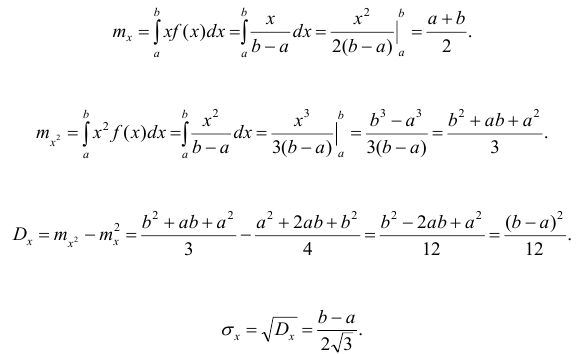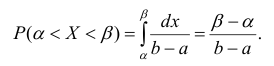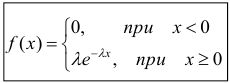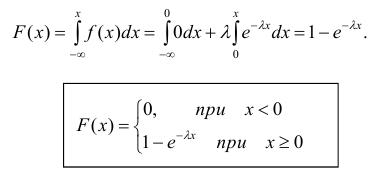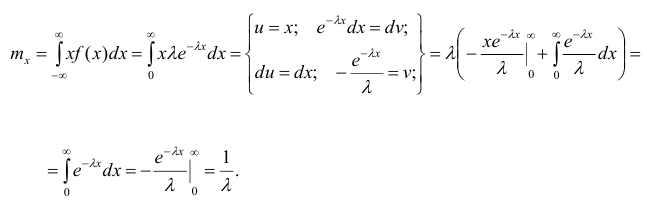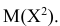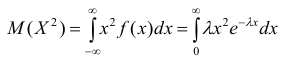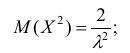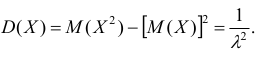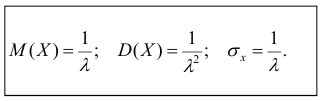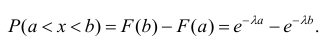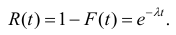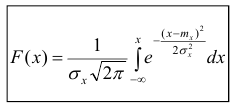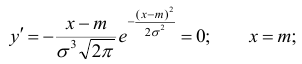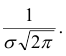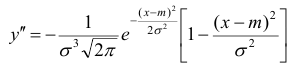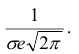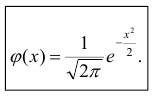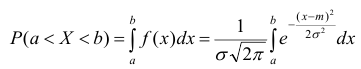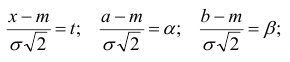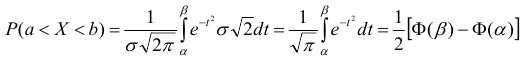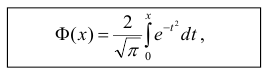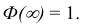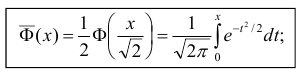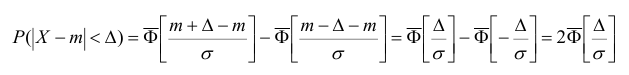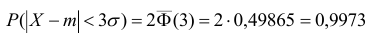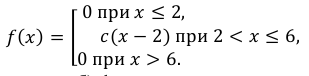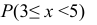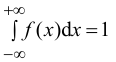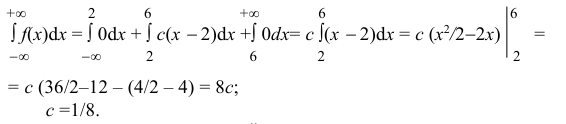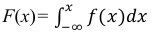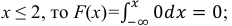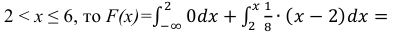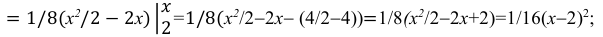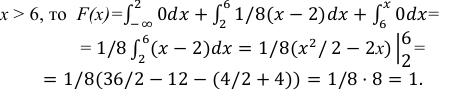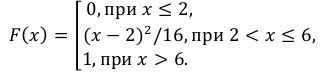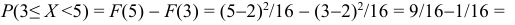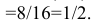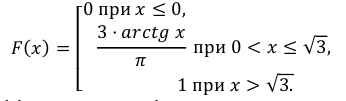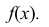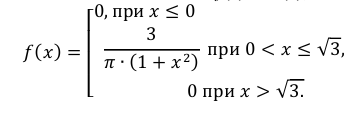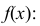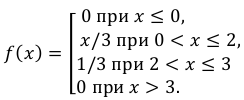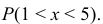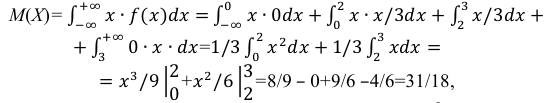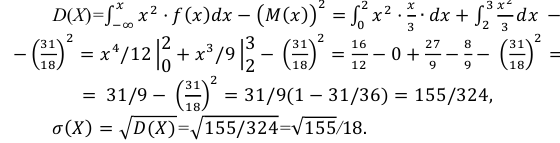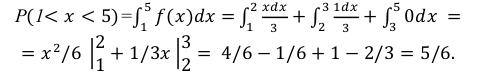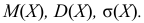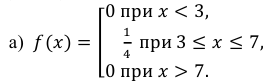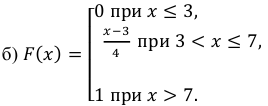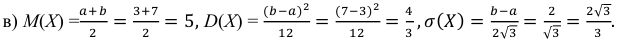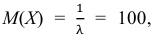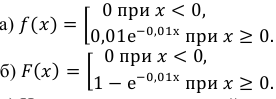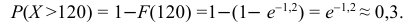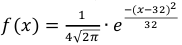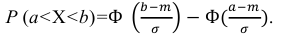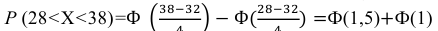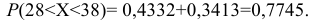Как найти дифференциальную функцию случайной величины

Рассмотрим
непрерывную случайную величину.
Интегральная функция распределения
вероятностей
такой случайной величины непрерывно
дифференцируема.

Определение.
Производная
от интегральной функции распределения


непрерывной случайной величины называется
дифференциальной
функцией распределения
этой случайной величины или дифференциальным
законом распределения

.

Дифференциальная
функция распределения иначе называется
плотностью
распределения вероятности.

Поясним
это название. Из определения вероятности
следует

.

По
аналогии с массой стержня, отношение
вероятности того, что случайная величина
примет значение из интервала,
к длине этого интервала– это средняя плотность вероятности
случайной величины на этом интервале.

Предел
при
средней плотности вероятности случайной
величины – это плотность распределения
вероятностей.

Дифференциальную
функцию распределения поэтому обозначают
иногда через
.

Свойства дифференциальной функции распределения

Свойство
1.
Дифференциальная функция распределения
определена при всех действительных
значениях аргумента, т.е.

.

Доказательство.

Свойство
2.
Дифференциальная
функция распределения неотрицательна

.

Доказательство.

Свойство
3. Вероятность
того, что непрерывная случайная величина
примет значение на промежутке,
равна определенному интегралу от ее
плотности распределения, взятому в
пределах отдо.

. (1)

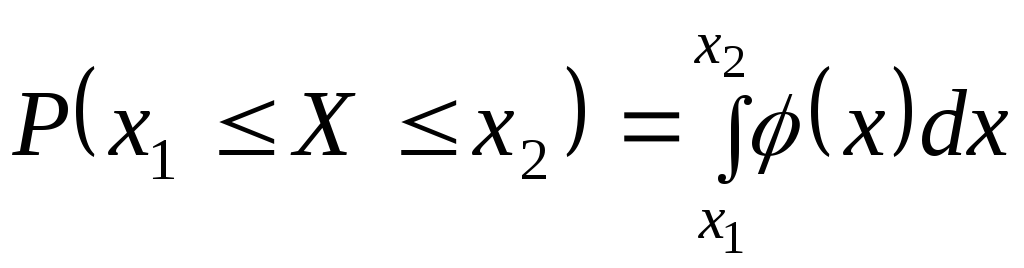
Доказательство.

Рассмотрим
геометрическую интерпретацию свойства
3.

Определение. График дифференциальной функции распределения называетсякривой распределения вероятностей случайной величины . Исходя из геометрического смысла определенного интеграла. Делаем заключение: вероятность того, что случайная величина примет значение на промежутке , равна

площади
криволинейной трапеции, ограниченной
сверху кривой распределения вероятностей
,
слева прямой

Свойство
4.
Если
известна дифференциальная функция
непрерывной случайной величины, то ее
интегральная функция определяется по
формуле

.

Доказательство.

Свойство
5.
Несобственный
интеграл первого рода от дифференциальной
функции в бесконечных пределах равен
единице

.

Доказательство.

Замечание
1. Если
все возможные значения случайной
величины
содержатся в промежутке,
то они тем более содержатся в интервале,
а поэтому событие

,

следовательно

и

.

Замечание
2.
Свойства 1 и 2 являются характеристическими
свойствами дифференциальной функции
распределения случайной величины, т.е.,
по доказанному, любая дифференциальная
функция распределения случайной величины
обладает свойствами 1, 2, и, наоборот,
любая функция, обладающая свойствами
1 и 2, является дифференциальной функции
распределения некоторой случайной
величины.

Пример.
Дифференциальная функция распределения
случайной величины задана формулой

.

Найти:
а)
коэффициент
и плотность распределения случайной
величины;

б)
интегральную функцию распределения
заданной случайной величины;

в)
вероятность того, что случайная величина
примет значение на промежутке.

Решение.
а)

Пример.
Случайная
величина
задана интегральной функций распределения

.

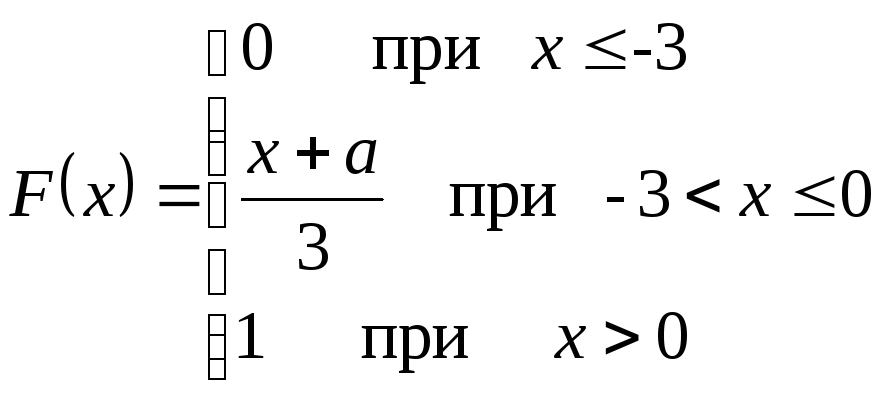
Найти:
а)
значение параметра
;

б)дифференциальную
функцию распределения; построить графики
интегральной и

дифференциальной
функций распределения;

в)
вероятность того, что случайная величина
примет значение на промежутке.

Решение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Плотность распределения вероятностей непрерывной случайной величины

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Краткая теория

---

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

 называют функцию

 – первую производную от функции распределения

:

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

 примет
значение, принадлежащее интервалу

 равна
определенному интегралу от плотности распределения, взятому в пределах от

 до

:

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

 и прямыми

 и

.

В частности, если

 – четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

 можно найти
функцию распределения

 по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

 до

 равен единице:

Смежные темы решебника:

• Дискретная случайная величина
• Непрерывная случайная величина
• Интегральная функция распределения вероятностей

Примеры решения задач

---

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1;  β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

 найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

 найдем из
формулы:

Учитывая
свойства

,  сразу можем
отметить, что:

Остается
найти выражение для

, когда

 принадлежит
интервалу

.

Получаем:

3) Построим графики

 и

:

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

:

---

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

 найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле: 

---

Пример 3

Непрерывная
случайная величина

 имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

 найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

---

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5;  11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

---

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

---

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

---

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

---

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

 задана плотностью распределения вероятностей.

Требуется
найти:

– функцию
распределения вероятностей;

–
математическое ожидание;

–
дисперсию;

– среднее
квадратическое отклонение;

– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

–
построить графики функции распределения и плотности распределения вероятностей.

---

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

---

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

–
составить функцию плотности распределения и построить ее график;

– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

---

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

---

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

---

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

---

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

 

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Содержание:

Непрерывные случайные величины: функция распределения случайной величины:

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Функция распределения непрерывной случайной величины

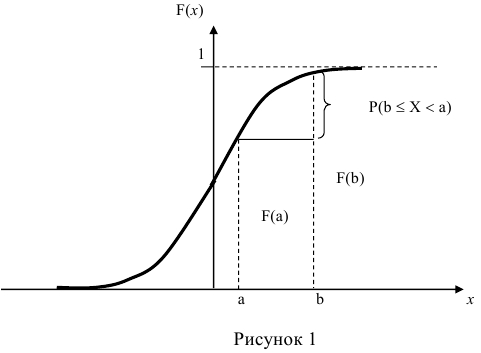
Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.

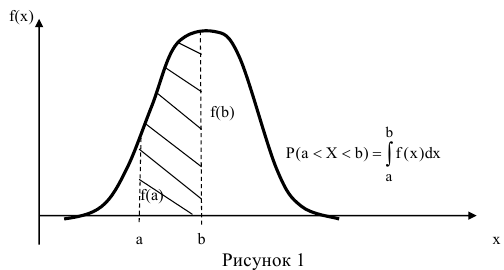
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).

Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Пусть х – действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т.е. X

Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х.

F(x) = Р(Х < х)

Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Для дискретной случайной величины функция распределения имеет

Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

Функция распределения дискретной случайной величины X разрывна и возрастает скачками при переходе через каждое значение

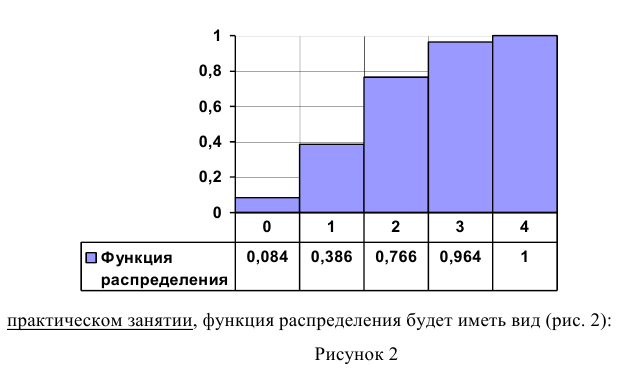
Так для примера, который мы будем рассматривать на следующем

Свойства функции распределения

1)    значения функции распределения принадлежат отрезку [0, 1].

2)    F(x) – неубывающая функция.

3)    Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.

4)    На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5)    Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Плотность вероятности. Числовые характеристики. Моменты случайных величин

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности
распределения.

Плотность распределения

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Определение. Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x) – первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина X в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина X называется непрерывной, если её функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек).

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина X примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b.

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения (см. лекцию тема № 10).

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми х=а и х=b.

Геометрически вероятность Р(а < X < b) представляется в виде заштрихованной области, ограниченной кривой распределения и осью Ох на интервале(а; b) (рис 1).

Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:

Свойства плотности распределения

1) Плотность распределения – неотрицательная функция.

2) Несобственный интеграл от плотности распределения в пределах от –
равен единице.

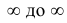
Плотность распределения
можно представить как:

тогда
Поэтому иногда функцию плотности распределения f(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X, а функцию распределения F(x) -интегральной функцией распределения или интегральным законом распределения.

Следует заметить, что интеграл 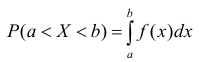возможно трактовать как сумму бесконечно большого числа несовместных элементарных событий, каждое из которых заключается в попадании случайной величины в бесконечно малый участок (х, х + dx) и имеет вероятность:

Р(х < X < х + dx) = dF(x) = f(x)dx

Величину f(x)dx называют элементом вероятности.

По своему содержанию элемент вероятности есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке X.

Функция распределения случайной величины X по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от

В схеме непрерывных случайных величин можно вывести аналогии формулы полной вероятности и формулы Бейеса, рассмотренные при изучении темы 4.

Обозначим Р(А /х) условную вероятность события А при условии Х= х. Заменяя в формуле полной вероятности вероятность гипотезы элементом вероятности f(x)dx, а сумму – интегралом, получим полную вероятность события А.

Данная формула называется интегральной формулой полной вероятности.

Соответствующий аналог в схеме непрерывных случайных величин имеет и формула Бейеса. Обозначив условную плотность распределения случайной величины X при условии, что в результате опыта появилось событие A через 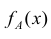, получим:

Данная формула называется интегральной формулой Бейеса.

Числовые характеристики непрерывных случайных величин

Пусть непрерывная случайная величина X задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [а,b].

Математическое ожидание

Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называется определенный интеграл

Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

При этом, конечно, предполагается, что несобственный интеграл сходится.

Дисперсия

Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата её отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

 

Среднеквадратичное отклонение

Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.

Мода

Определение. Модой 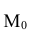дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно
называется антимодальным.

Медиана

Определение. Медианой 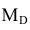случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Начальный момент

Определение. Начальным моментом порядка k случайной величины X называется математическое ожидание величины

Для дискретной случайной величины:
Для непрерывной случайной величины:

Начальный момент первого порядка равен математическому ожиданию.

Центральный момент

Определение. Центральным моментом порядка k случайной величины X называется математическое ожидание величины

Для дискретной случайной величины:

Для непрерывной случайной величины:
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
 

Коэффициент асимметрии

Определение. Отношение центрального момента третьего порядка к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.

 

Эксцесс

Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: 

Абсолютный центральный момент:

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.

Законы распределения непрерывных величин: нормальное, равномерное, показательное

В материалах сегодняшней лекции мы рассмотрим законы распределения непрерывных величин.

Равномерное распределение

Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность

распределения случайной величины постоянна, а вне его равна нулю.

Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения, представленной на рис. 1
        

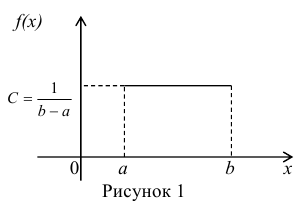
Получаем        .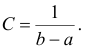

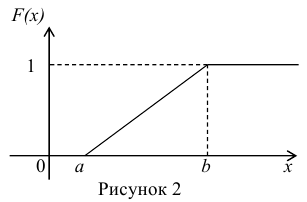
Найдём функцию распределения F(x) на отрезке [а,b] (рис. 2).

Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы её значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.

Вероятность попадания случайной величины в заданный интервал:

 

Показательное распределение

Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью    

где 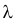– положительное число.

Найдём закон распределения.

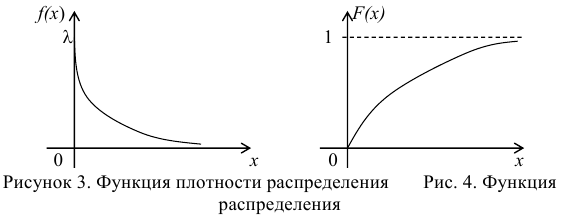
Графики функции распределения и плотности распределения представлены на рис. 3, 4.

Найдём математическое ожидание случайной величины, подчинённой показательному распределению.

Результат получен с использованием того факта, что

Для нахождения дисперсии найдём величину

Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:

Тогда
Итого:

Видно, что в случае показательного распределения математическое ожидание и среднеквадратическое отклонение равны.

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.

Показательное распределение широко используется в теории надёжности.

Допустим, некоторое устройство начинает работать в момент времени to=0, а через какое- то время t происходит отказ устройства.

Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.

Таким образом, функция распределения F(t) = P(T

Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) – l – F(t).

Функция надежности

Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надёжности для какого- либо устройства при показательном законе распределения равна:

Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов 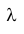и не зависит от безотказной работы устройства в
прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 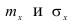входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.

Найдём функцию распределения F(x).

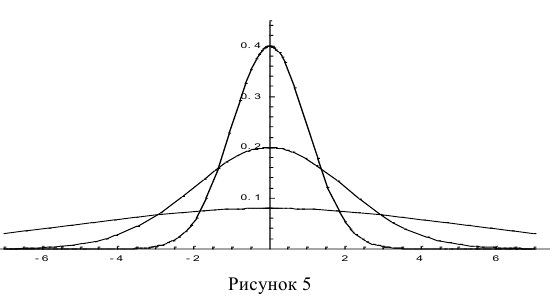
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1)    Функция определена на всей числовой оси.

2)    При всех х функция распределения принимает только положительные значения.

3)    Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л значение функции стремится к нулю.

4)    Найдём экстремум функции.

Т.к. при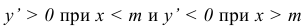 , то в точке х = m функция имеет максимум, равный

5)    Функция является симметричной относительно прямой x = а, т.к. разность

(х – а) входит в функцию плотности распределения в квадрате.

6)    Для нахождения точек перегиба графика найдем вторую производную функции плотности.

При 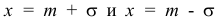вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно     
Построим график функции плотности распределения (рис. 5).

Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения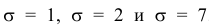. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и 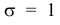кривая называется нормированной. Уравнение нормированной кривой:

Функция Лапласа

Найдём вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

Обозначим

Тогда
Т.к. интеграл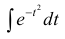 не выражается через элементарные функции, то вводится в рассмотрение функция

которая называется функцией Лапласа или интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

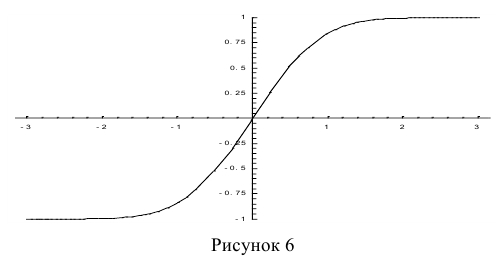
На рис. 6 показан график функции Лапласа.

Функция Лапласа обладает следующими свойствами:

• 1)    Ф(0) = 0;
• 2)    Ф(-х) = – Ф(х);
• 3)  

Функцию Лапласа также называют функцией ошибок и обозначают
erf х.

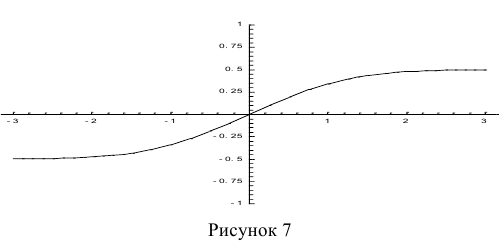
Ещё используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

На рис. 7 показан график нормированной функции Лапласа.

Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины

Если принять 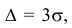, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой-либо случайной величины выполняется правило трёх сигм, то эта случайная величина имеет нормальное распределение.

Пример:

Случайная величина Х задана плотностью распределения вероятностей:

Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в)
 

Решение:

а) Значение с найдем из условия нормировки:
Следовательно,

б) Известно, что 

Поэтому, если 

если 

если 

Таким образом,

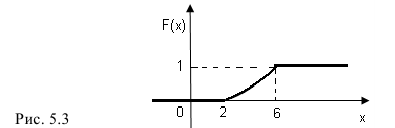
График функции F(х) изображен на рис. 5. 3.

в) 

Пример:

Случайная величина Х задана функцией распределения:

Найти дифференциальную функцию распределения  
 

Решение:  

Так как 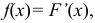 то

Пример:

Случайная величина Х задана дифференциальной функцией

Найти 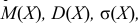 а также 

Решение:

Некоторые законы распределения непрерывной случайной величины 

Пример:

Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:

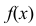
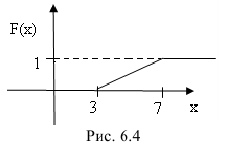
а) плотность распределения вероятностей  и построить ее график;

б) функцию распределения 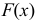 и построить ее график;

в)
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:

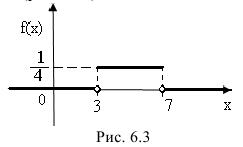
Построим ее график (рис. 6.3):

Построим ее график (рис. 6.4):

Пример:

Среднее время безотказной работы прибора равно 100 ч.
Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:

а) плотность распределения вероятностей;

б) функцию распределения;

в) вероятность того, что время безотказной работы прибора превысит 120 ч.
 

Решение.

По условию математическое ожидание
откуда 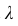 = 1/100 = 0,01.
Следовательно,

в) Искомую вероятность найдем, используя функцию распределения: 

Пример:

Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а) плотность распределения вероятностей 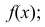 б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
 

Решение:

По условию m = 32, σ2 = 16, следовательно, σ = 4, тогда

а) 

б) Воспользуемся формулой:

Подставив a = 28, b = 38, m = 32, σ = 4, получим

По   таблице   значений   функции   Ф(х)   находим   Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Итак, искомая вероятность:

Заключение по лекции:

В лекции мы рассмотрели законы распределения непрерывных величин.

ЛЕКЦИЯ 9

ТЕМА: ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ

1.     
Равномерный закон распределения.

2.     
Нормальный закон распределения.

2.1.
Интегральная и дифференциальная функции
распределения. Вероятность попадания в
заданный интервал.

2.2.
Вычисление вероятности заданного
отклонения.

2.3.
Правило трех сигм.

3.     
Показательный закон распределения.

3.1.
Интегральная и дифференциальная функции
распределения.

3.2.
Числовые характеристики.

3.3.
Функция надежности.

   
 

1.     
Равномерный
закон распределения.

На
практике встречаются случайные величины, о
которых заранее известно, что они могут
принять какое-либо значение в строго
определенных границах, причем в этих
границах все значения случайной величины
имеют одинаковую вероятность (обладают
одной и той же плотностью вероятностей).

Например,
при поломке часов остановившаяся минутная
стрелка будет с одинаковой вероятностью (плотностью
вероятности) показывать время, прошедшее от
начала данного часа до поломки часов. Это
время является случайной величиной,
принимающей с одинаковой плотностью вероят­ности
значения, которые не выходят за границы,
определенные продолжительностью одного
часа. К подобным случайным величинам
относится также и погрешность округления.
Про такие величины говорят, что они
распределены равномерно, т. е. имеют
равномерное распределение.

Определение.
Непрерывная случайная величина Х имеет
равномерное распределение на отрезке [а,
в], если на этом
отрезке плотность распределения
вероятности случайной величины постоянна,
т. е. если дифференциальная функция
распределения f(х)
имеет следующий вид:

Иногда
это распределение называют законом
равномерной плотности. Про величину,
которая имеет равномерное распределение на
некотором отрезке, будем говорить, что она
распределена равномерно на этом отрезке.

Найдем
значение постоянной с. Так как площадь,
ограниченная кривой распределения и осью Ох,
равна 1, то

откуда
с=1/(b–a).

Теперь
функцию f(x)
можно представить в виде

 

Построим
функцию распределения F(x), для чего найдем выражение F(x)
на интервале [a, b]:

Графики
функций f(x)
и F(x)
имеют вид:

Найдем
числовые характеристики.

Используя
формулу для вычисления математического
ожидания НСВ, имеем:

Таким
образом, математическое ожидание случайной
вели­чины, равномерно распределенной на
отрезке [a, b]
совпадает с серединой этого отрезка.

Найдем
дисперсию равномерно распределенной
случайной величины:

откуда
сразу же следует, что среднее
квадратическое отклонение:

Найдем
теперь вероятность попадания значения
случайной величины, имеющей равномерное
распределение, на интервал (a,b),
принадлежащий целиком
отрезку [a,
b]:

Геометрически
эта вероятность представляет 
собой  площадь
заштрихованного прямоугольника. Числа а
и b называются параметрами
распределения и однозначно
определяют равномерное распределение.

Пример1.
Автобусы некоторого маршрута идут строго
по расписанию. Интервал движения 5 минут.
Найти вероятность того, что пассажир,
подошедший к остановке. Будет ожидать
очередной автобус менее 3 минут.

Решение:

СВ-
время ожидания автобуса имеет равномерное
распределение. Тогда искомая вероятность
будет равна:

Пример2.
Ребро куба х измерено приближенно. Причем

 

Рассматривая
ребро куба как случайную величину,
распределенную равномерно в интервале (a,
b),
найти математическое ожидание и дисперсию
объема куба.

Решение:

Объем
куба- случайная величина, определяемая
выражением У= Х³. Тогда математическое
ожидание равно:

Дисперсия:

 

2.
Нормальный закон  распределения.

2.1.Интегральная
и дифференциальная функции распределения.
Вероятность попадания в заданный интервал.

Одним
из наиболее часто встречающихся
распределений является нормальное
распределение. Оно играет большую роль в
теории вероятностей и занимает среди
других распределений особое положение.
Нормальный закон распределения является
предельным законом, к которому
приближаются другие законы распределения
при часто встречающихся аналогичных
условиях.

Если
предоставляется возможность рассматривать
некоторую случайную величину как сумму
достаточно большого числа других случайных
величин, то данная случайная величина
обычно подчиняется нормальному закону
распределения. Суммируемые случайные
величины могут подчиняться каким угодно
распределениям, но при этом должно
выполняться условие их независимости (или
слабой зависимости). При соблюдении
некоторых не очень жестких условий
указанная сумма случайных величин
подчиняется приближенно нормальному
закону распределения и тем точнее, чем
большее количество величин суммируется.

Ни
одна из суммируемых случайных величин не
должна резко отличаться от других, т. е.
каждая из них должна играть в общей сумме
примерно одинаковую роль и не иметь
исключительно большую по сравнению с
другими величинами дисперсию.

Для
примера рассмотрим изготовление некоторой
детали на станке-автомате. Размеры
изготовленных деталей несколько
отличаются от требуемых. Это отклонение
размеров от стандарта вызывается
различными причинами, которые более или
менее независимы друг от друга. К ним могут
относиться:

неравномерный
режим обработки детали; неоднородность
обрабатываемого материала; неточность
установки заготовки в станке; износ
режущего инструмента и деталей станков;

упругие
деформаций узлов станка; состояние
микроклимата в цехе; колебание напряжения в
электросети и т. д. Каждая из перечисленных
и подобных им причин влияет на отклонение
размера изготовляемой детали от стандарта.
Таким образом, общее отклонение размера,
фиксируемое измерительным прибором,
является суммой большего числа отклонений,
обусловленных различными причинами. Если
ни одна из этих причин не является
доминирующей, то суммарное отклонение
является случайной величиной, имеющей
нормальный закон распределения.

Так
как нормальному закону подчиняются только
непрерывные случайные величины, то это
распределение можно задать в виде
плотности распределения вероятности.

Определение:
Непрерывная случайная величина Х имеет
нормальное распределение (распределена по
нормальному закону), если плотность
распределения вероятности f(x) имеет вид

где
а
и s—некоторые
постоянные, называемые параметрами
нормального распределения.

Функция
распределения F(x) в
рассматриваемом случае принимает вид

Параметр
а– есть
математическое ожидание НСВХ, имеющей
нормальное распределение, s –
среднее квадратическое
отклонение, тогда дисперсия равна

 Выясним геометрический смысл
параметров распределения а
и s.
Для этого исследуем
поведение функции f(x).
График функции f(x)
называется нормальной кривой.

Рассмотрим
свойства функции f(x):

1°.
Областью определения функции f(x)
является вся числовая ось.

2°.
Функция f{x)
может принимать только положительные
значения, т. е. f(x}>0.

3°.
Предел функции f(x) при
неограниченном возрастании |х| равен нулю,
т. е. ось ОХ является горизонтальной
асимптотой графика функции.

     
4°. Функция f{x)
имеет в точке х =
a  максимум,
равный

5°.
График функции f(x)
симметричен относительно прямой х =
а.

6°.
Нормальная кривая в точках х = а
+s 
имеет перегиб,

 

На
основании доказанных свойств построим
график плотности нормального
распределения f(x).

Использование
формул  f(x)
и F(x)
для практических расчетов затруднительно.
Но решение задач по этим 
формулам  можно
упростить, если от нормального
распределения с произвольными параметрами а и s
перейти 
к нормальному распределению с
параметрами а=0, s

= 1.

Функция
плотности нормального распределения f(x)
с параметрами а=0, s 
=1 называется плотностью
стандартной нормальной
случайной величины и ее график имеет вид:

Функция
плотности и интегральная функция
стандартной нормальной СВ будут иметь вид:

Для
вычисления вероятности попадания СВ в
интервал (a,
b) воспользуемся
функцией    Лапласа:

Перейдем
к стандартной нормальной случайной
величине

 

 

Тогда

Значения
функции Ф(u) необходимо взять из таблицы
приложений “Таблица значений функции Ф(х)”
.

Пример.
Случайная величина Х распределена по нормальному
закону. Математическое
ожидание и среднее квадратическое
отклонение этой величины соответственно
равны 30 и 10. Найти вероятность того, что Х
примет значение, принадлежащее интервалу
(10, 50).

Решение:

 По
условию:a  =10,
b=50, а=30,
s =10,
следовательно,

По
таблице  находим Ф
(2) = 0,4772. Отсюда, искомая вероятность:

Р(10
< Х < 50) =2×0,4772=0,9544.

2.2.
Вычисление вероятности заданного
отклонения

Часто
требуется вычислить вероятность того, что
отклонение нормально распределенной
случайной вели­чины Х
по абсолютной величине меньше заданного
положительного числа d,
т. е. требуется найти
вероятность осуществления неравенства  |x
—а|<d.

Заменим
это неравенство равносильным ему двойным
неравенством

Тогда
получим:

Приняв
во внимание равенство:

(функция
Лапласа—нечетная), окончательно
имеем

Вероятность
заданного отклонения равна

На
рисунке наглядно показано, что если две
случайные величины нормально распределены
и а
= 0, то вероятность
принять значение, принадлежащее интервалу (-d,d),больше у
той величины, которая имеет меньшее
значение d.
Этот факт полностью
соответствует вероятностному смыслу
параметра s
.

Пример.
Случайная величина Х
распределена нормально. Математическое
ожидание и среднее квадратическое
отклонение Х соответственно равны 20 и 10. Найти
вероятность того, что отклонение по
абсолютной величине будет меньше трех.

Решение:
Воспользуемся
формулой

 

 По
условию ,

тогда

2.3.
Правило трех сигм

                               

Преобразуем
формулу   

 

 

Введем
обозначение

Тогда
получим:

 

Если
t=3,
то

т.
е. вероятность того, что отклонение по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973.

Другими
словами, вероятность того, что абсолютная
величина отклонения превысит утроенное
среднее квадратическое отклонение, очень
мала, а именно равна  0,0027=1-0,9973.
Это означает, что лишь в 0,27% случаев так
может произойти. Такие события, исходя из
принципа невозможности маловероятных
событий можно считать практически
невозможными. В этом и состоит сущность
правила трех сигм:

Если случайная величина
распределена нормально, то абсолютная
величина ее отклонения от математиче­ского
ожидания не превосходит утроенного
среднего квадратического отклонения.

На
практике правило трех сигм применяют так:
если распределение изучаемой случайной
величины неизвестно, но условие, указанное
в приведенном правиле, выполняется, то есть
основание предполагать, что изучаемая
величина распределена нормально; в
противном случае она не распределена
нормально.

3.     
Показательное
распределение.

3.1. 
Интегральная и дифференциальная
функции распределения.

Определение:
Непрерывная случайная величина X, функция
плотности которой задается выражением

называется случайной
величиной, имеющей показательное, или
экспоненциальное, распределение.

Величина
срока службы различных устройств и времени
безотказной работы отдельных элементов
этих устройств при выполнении определенных
условий обычно подчиняется показательному
распределению. Другими словами, величина
промежутка времени между появлениями двух
последовательных редких событий
подчиняется зачастую показательному
распределению.

Как
видно из формулы , показательное
распределение определяется только одним
параметром m.

Найдем
функцию распределения показательного
закона, используя свойства
дифференциальной функции распределения:

Графики
дифференциальной и интегральной функций
показательного распределения имеют вид:

3.2.
Числовые характеристики.

Используя
формулы для вычисления математического
ожидания, дисперсии и среднего
квадратического отклонения нетрудно
убедится, что для показательного
распределения

 

 .

Таким
образом, для показательного распределения
характерно, что среднее квадратическое
отклонение численно равно математическому
ожиданию.

Найдем
вероятность попадания СВ в интервал (a,b):

3.3.
Функция надежности.

Пусть
некоторое устройство начинает работать в
момент времени t₀
= 0, а по истечении времени длительностью t происходит отказ. Обозначим
через Т НСВ – длительность времени
безотказной работы устройства. Если
устройство проработало безотказно время
меньшее t,
то, следовательно, за время длительностью t наступит отказ. Тогда
функция распределения F(t)=P(T<t)=1- e^–mt определяет
вероятность отказа устройства за время t.

Найдем
вероятность противоположного события-
безотказной работы за время t:

.

Функция
R(t)
называется функцией надежности.

Выясним
смысл числовых характеристик и параметра
распределения.

Математическое
ожидание – это среднее время между двумя
ближайшими отказами устройства, а величина
обратная математическому ожиданию
(параметр распределения)- интенсивность
отказов, т.е. количество отказов в единицу
времени.

Пример.
Время безотказной работы устройства
распределено по закону

 

Найти
среднее время безотказной работы
устройства, вероятность того, что
устройство не откажет за среднее время
безотказной работы. Найти вероятность
отказа за время t= 100
часов.

Решение:

По
условию интенсивность отказов m
=0,02. Тогда
среднее время между двумя отказами, т.е.
математическое ожидание М(Х)=1/0,02=50часов.
Вероятность безотказной работы за этот
промежуток времени вычислим по функции
надежности:

По
функции F(t)
вычислим вероятность отказа за время t
=100
часов:

Контрольные
вопросы.

1.     
Сформулировать равномерный закон
распределения. Записать дифференциальную и
интегральную функции.

2.     
Записать формулы для вычисления
числовых характеристик равномерно
распределенной случайной величины.

3.     
Сформулировать нормальный закон
распределения. Записать дифференциальную и
интегральную функции.

4.     
Описать свойства дифференциальной
функции нормально распределенной
случайной величины. Пояснить
геометрический смысл параметров
нормального распределения.

5.     
При каких значениях параметров функция
плотности нормального распределения
называется плотностью стандартной
нормальной случайной величины?

6.     
Записать формулу для вычисления
вероятности отклонения нормально
распределенной СВ от математического
ожидания.

7.     
Сформулировать правило трех сигм и
пояснить его суть.

8.     
Сформулировать показательный закон
распределения. Записать дифференциальную и
интегральную функции.

9.     
Каков смысл параметра показательного
распределения, если в качестве СВ
рассматривать время безотказной работы
устройства? Какими выражениями параметр
распределения связан с числовыми
характеристиками?

10. 
Вероятность какого события определяет
функция надежности?

1