Содержание:
- Случай независимой переменной
- Случай зависимой переменной
Пусть функция $y=f(x)$ зависит от переменной
$x$ и дифференцируема в точке
$x$. Может оказаться, что в точке
$x$ дифференциал
$d y=f^{prime}(x) d x$, рассматриваемый как функция от
$x$, есть также дифференцируемая функция. Тогда существует
дифференциал от дифференциала $d(dy)$ данной функции,
который называется дифференциалом второго порядка функции $y=f(x)$.
Дифференциал второго порядка обозначается следующим образом:
$d^2y=d(dy)$
Аналогично определяются дифференциалы более высоких порядков.
Определение
Дифференциалом
$n$-го порядка
$d_ny$ функции
$y=f(x)$ называется дифференциал от дифференциала
$(n-1)$-го порядка этой функции, то есть
$$d^{n} y=dleft(d^{n-1} yright)$$
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Пусть $y=f(x)$ – функция независимой переменной
$x$, имеющая дифференциалы любого порядка.
Первый дифференциал функции
$$d y=f^{prime}(x) d x$$
где $dx=Delta x$ – некоторое приращение независимой
переменной $x$, которое мы задаем сами и которое не
зависит от $x$. По определению
$$d^{2} y=d(d y)=dleft(f^{prime}(x) d xright)$$
Переменной является аргумент $x$. Значит, для
дифференциала величина $dx$ является постоянной и
поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
$$d^{2} y=dleft(f^{prime}(x) d xright)=d x cdot dleft(f^{prime}(x)right)$$
Для вычисления дифференциала $dleft(f^{prime}(x)right)$ применим формулу
дифференциала первого порядка к функции $f^{prime}(x)$. Тогда получим:
$$dleft(f^{prime}(x)right)=left(f^{prime}(x)right)^{prime} cdot d x=d x cdot f^{prime prime}(x) d x=f^{prime prime}(x)(d x)^{2}=f^{prime prime}(x) d x^{2}$$
Итак,
$$d^{2} y=f^{prime prime}(x) d x^{2}$$
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
$n$-го порядка:
$$d^{n} y=f^{n}(x) d x^{n}$$
Пример
Задание. Найти дифференциал третьего порядка функции $y(x)=4x^3-12x+5$
Решение. По формуле
$$d^{3} y=y^{prime prime prime}(x) d x^{3}$$
Найдем третью производную заданной функции:
$$begin{array}{c}
y^{prime}(x)=left(4 x^{3}-12 x+5right)^{prime}=left(4 x^{3}right)^{prime}-(12 x)^{prime}+(5)^{prime}= \
4left(x^{3}right)^{prime}-12(x)^{prime}+0=4 cdot 3 x^{2}-12 cdot 1=12 x^{2}-12 \
y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(12 x^{2}-12right)^{prime}=left(12 x^{2}right)^{prime}-(12)^{prime}= \
=12left(x^{2}right)^{prime}-0=12 cdot 2 x=24 x \
y^{prime prime prime}(x)=left(y^{prime prime}(x)right)^{prime}=(24 x)^{prime}=24(x)^{prime}=24
end{array}$$
Тогда
$$d^{3}y=24dx^3$$
Ответ. $d^{3}y=24dx^3$
Случай зависимой переменной
Пусть задана дифференцируемая функция $y=f(u(x))$. Тогда
$$d y=f^{prime}(u) d u$$
где $d u=u^{prime}(x) d x$ в общем случае не является постоянной величиной.
Поэтому дифференциал от функции $f^{prime}(u) d u$ берем как дифференциал от произведения
$$d^{2} y=dleft(f^{prime}(u) d uright)=dleft(f^{prime}(u)right) cdot d u+f^{prime}(u) cdot d(d u)=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти дифференциал второго порядка
$d^{2}u$ функции $f(u)=sqrt{u}$, где
$u(x)=3x+7$ и $x$ – независимая переменная.
Решение. Решим пример разными способами и сравним ответы.
1-ый способ. Согласно формуле, имеем, что искомый дифференциал
$$d^{2} y=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$
Найдем все необходимые компоненты формулы. Из условия имеем:
$$begin{array}{c}
f^{prime}(u)=(sqrt{u})^{prime}=frac{1}{2 sqrt{u}} \
f^{prime prime}(u)=left(f^{prime}(u)right)^{prime}=left(frac{1}{2 sqrt{u}}right)^{prime}=frac{1}{2} cdotleft(u^{-frac{1}{2}}right)^{prime}= \
=frac{1}{2} cdotleft(-frac{1}{2}right) cdot u^{-frac{3}{2}}=-frac{1}{4 sqrt{u^{3}}} \
d u=d(3 x+7)=(3 x+7)^{prime} d x=left[(3 x)^{prime}+(7)^{prime}right] d x= \
=left[3(x)^{prime}+0right] d x=3 cdot 1 cdot d x=3 d x \
d^{2} u=d(3 d x)=d x cdot d(3)=d x cdot 0=0
end{array}$$
А тогда:
$$begin{aligned}
d^{2} y=&-frac{1}{4 sqrt{u^{3}}} d u^{2}+frac{1}{2 sqrt{u}} cdot 0=-frac{1}{4 sqrt{u^{3}}} cdot(3 d x)^{2}=\
&=-frac{9}{4 sqrt{u^{3}}} d x^{2}=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}
end{aligned}$$
2-ой способ. Из того, что $f(u)=sqrt{u}$ и
$u(x)=3 x+7$, получаем:
$$f(x)=sqrt{3 x+7}$$
А тогда
$$d^{2} y=f^{prime prime}(x) d x^{2}$$
Найдем вторую производную функции $f(x)=sqrt{3 x+7}$:
$$f^{prime}(x)=(sqrt{3 x+7})^{prime}=frac{1}{2 sqrt{3 x+7}} cdot(3 x+7)^{prime}=$$
$$=frac{1}{2 sqrt{3 x+7}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=frac{1}{2 sqrt{3 x+7}} cdotleft[3(x)^{prime}+0right]=$$
$$=frac{3 cdot 1}{2 sqrt{3 x+7}}=frac{3}{2 sqrt{3 x+7}}$$
$$f^{prime prime}(x)=left(f^{prime}(x)right)^{prime}=left(frac{3}{2 sqrt{3 x+7}}right)^{prime}=frac{3}{2}left((3 x+7)^{-frac{1}{2}}right)^{prime}=$$
$$=frac{3}{2} cdotleft(-frac{1}{2}right) cdot(3 x+7)^{-frac{3}{2}} cdot(3 x+7)^{prime}=$$
$$=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdot 3(x)^{prime}=$$
$$=-frac{3 cdot 3 cdot 1}{4 sqrt{(3 x+7)^{3}}}=-frac{9}{4 sqrt{(3 x+7)^{3}}}$$
Окончательно имеем:
$$d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$$
Ответ. $d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$
Читать дальше: производная функции, заданной неявно.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 сентября 2019 года; проверки требуют 7 правок.
Дифференциалом порядка n, где n > 1, от функции 
.
Дифференциал высшего порядка функции одной переменной[править | править код]
Для функции, зависящей от одной независимой переменной 
,
.
Отсюда можно вывести общий вид дифференциала n-го порядка от функции 

.
При вычислении дифференциалов высших порядков очень важно, что 



Дифференциал высшего порядка функции нескольких переменных[править | править код]
Если функция 

Символически общий вид дифференциала n-го порядка от функции

где 


Приращения 
Сложность выражения дифференциала возрастает с увеличением числа переменных.
Неинвариантность дифференциалов высшего порядка[править | править код]
При 




Так, для независимой переменной 
Если же переменная 

.
Аналогично, третий дифференциал примет вид:
.
Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
При 

С учётом зависимости 
Дополнения[править | править код]
-
- для функции с одной переменной:
,
;
- для функции с несколькими переменными:
,
Примечания[править | править код]
- ↑ 1 2 Баранова Елена Семеновна, Васильева Наталья Викторовна, Федотов Валерий Павлович. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие. 2-е изд.. — “Издательский дом “”Питер”””, 2012. — С. 196-197. — 400 с. — ISBN 9785496000123.
Литература[править | править код]
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
Дифференциалы высших порядков
Пусть у = f (х) дифференцируемая функция, а её аргумент х- независимая переменная. Тогда её первый дифференциал dy = f′ (x) dx есть также функция от х; можно найти дифференциал этой функции.
Дифференциал от дифференциала функции у = f (х) называется её вторым дифференциалом (или дифференциалом второго порядка) и обозначается d 2y или d 2 f (x):
d 2 y = f ′′ (x) dx 2
Здесь dx 2 обозначает (dx)2.
Аналогично определяется и находится дифференциал третьего порядка: d 3 y = d (d 2 y) = d (f ′′ (x) dx 2) = f ′′′ (x) dx 3.
Вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)–го порядка: d n y = d (d n – 1y) = f (n) (x) (dx) n.
Отсюда находим, что f (n)(x)= d n y . В частности, при n = 1, 2, 3 соответственно получаем: dxn
|
f ′(x)= |
dy |
, |
f ′′(x)= |
d 2 y |
, |
f ′′′(x)= |
d 3 y |
, т.е. производную функции можно рассматривать как |
|
dx |
dx2 |
dx3 |
отношение её дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Отметим, что все приведённые выше формулы справедливы только, если х – независимая переменная.
Пример. Найти d 2 y, если y = e 3x и х – независимая переменная. Решение: так как y′ = 3e 3x, y′′ = 9e 3x, то имеем d 2y = 9e 3x dx 2.
Правила Лопиталя
Правила Лопиталя применяются для раскрытия неопределённостей вида 00 и ∞∞ , которые называются основными.
Теорема 3. (Правило Лопиталя раскрытия неопределённостей вида 00 ).
Пусть функции f (x) и g (x) непрерывны и дифференцируемы в окрестности точки х0 и
|
обращаются в нуль в этой точке: f (x0) = g (x0) = 0. Пусть g′ (x) ≠ 0 в окрестности точки x0. Если |
|||||||||||||||||||||
|
существует предел |
lim |
f ′(x) |
= l , то |
lim |
f (x) |
= lim |
f ′(x) |
= l . |
|||||||||||||
|
g(x) |
g′(x) |
||||||||||||||||||||
|
x→x0 |
g |
′ |
x→ x0 |
x→ x0 |
|||||||||||||||||
|
(x) |
|||||||||||||||||||||
|
Пример. Найти lim1− cos6x . |
|||||||||||||||||||||
|
x→0 |
2x2 |
||||||||||||||||||||
|
Решение: lim |
1− cos 6x |
= |
0 |
п.Л. |
6sin 6x |
0 |
п.Л. |
36 cos 6x |
36 |
||||||||||||
|
= lim |
= |
= lim |
= |
= 9. |
|||||||||||||||||
|
x→0 |
2x |
2 |
x→0 |
4x |
x→0 |
4 |
4 |
||||||||||||||
|
0 |
0 |
Теорема 4. (Правило Лопиталя раскрытия неопределённостей вида ∞∞ ).
13

|
Пусть функции f (x) и g (x) непрерывны и дифференцируемы в окрестности точки х0 (кроме, |
|||||||
|
может быть, точки х0), в этой окрестности lim f (x)= lim g(x)= ∞ , g′ (x) ≠ 0. Если существует |
|||||||
|
f ′(x) |
f (x) |
f ′(x) |
x→ x0 |
x→ x0 |
|||
|
предел lim |
, то lim |
= lim |
. |
||||
|
g′(x) |
g(x) |
||||||
|
x→ x0 |
x→ x0 |
x→ x0 |
g′(x) |
tg 3x
Пример. Найти lim tg 5x
x→π2
Решение:
|
lim tg 3x = |
∞ = |
3 |
= lim 3cos |
2 |
5x |
= |
0 = |
|||||||||||||||||||
|
lim |
cos |
3x |
||||||||||||||||||||||||
|
п.Л. |
2 |
п.Л. |
||||||||||||||||||||||||
|
x→ |
π |
tg 5x |
x→ |
π |
5 |
x→ |
π |
5cos |
2 |
3x |
0 |
|||||||||||||||
|
2 |
∞ |
2 |
2 |
|||||||||||||||||||||||
|
cos2 5x |
||||||||||||||||||||||||||
|
= |
3 |
lim − 10 cos 5x sin 5x |
= lim sin10x |
= |
0 |
= |
lim10cos10x |
= 5 . |
||||||||||||||||||
|
5 x→ |
π |
− 6 cos 3x sin 3x |
x→ |
π |
sin6x |
x→ |
π |
6cos6x |
3 |
|||||||||||||||||
|
2 |
2 |
0 |
2 |
|||||||||||||||||||||||
Неопределённости вида [0∞], [∞ − ∞], [1∞], [∞ 0], [0 0] сводятся к двум основным путём тождественных преобразований.
Пусть f (x) → 0, и g (x) → 0 при х → х0. Тогда очевидны следующие преобразования:
|
lim(f (x)g(x))= [0 ∞]= lim |
f (x) |
= |
0 |
(или lim |
f (x) |
= |
∞ ). |
|||||||||||||||||||||||
|
1 |
0 |
1 |
||||||||||||||||||||||||||||
|
x→ x |
0 |
0 |
0 |
∞ |
||||||||||||||||||||||||||
|
x→ x |
x→ x |
|||||||||||||||||||||||||||||
|
g(x) |
g(x) |
|||||||||||||||||||||||||||||
|
Пример. |
Найти limtg |
π x |
(2 − x). |
|||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||
|
x→2 |
||||||||||||||||||||||||||||||
|
Решение: |
2 − x |
= 0 = lim |
−1 |
= 4 . |
||||||||||||||||||||||||||
|
limtg π x (2 − x)= [∞ 0]= lim |
||||||||||||||||||||||||||||||
|
п.Л. |
||||||||||||||||||||||||||||||
|
4 |
0 |
|||||||||||||||||||||||||||||
|
x→2 |
x→2 |
π x |
1 |
π |
||||||||||||||||||||||||||
|
ctg 4 |
x→2 |
− |
||||||||||||||||||||||||||||
|
sin |
2 π x |
π |
||||||||||||||||||||||||||||
|
4 |
4 |
|||||||||||||||||||||||||||||
Пусть f (x) → ∞, и g (x) → ∞ при х → х0. Тогда можно поступить так:
|
1 |
1 |
||||||||||||||||||
|
1 |
1 |
− |
0 |
||||||||||||||||
|
lim(f (x)− g(x))= [∞ − ∞]= lim |
g(x) |
f (x) |
|||||||||||||||||
|
− |
= lim |
= |
. |
||||||||||||||||
|
1 |
1 |
1 |
1 |
0 |
|||||||||||||||
|
x→ x0 |
x→ x0 |
x→ x0 |
|||||||||||||||||
|
f (x) |
g(x) |
g(x) |
f (x) |
Пусть f (x) → 1, и g (x) → ∞, или f (x) → ∞, и g (x) → 0, или f (x) → 0, и g (x) → 0 при х → х0.
Для нахождения предела вида lim f (x)g (x ) вспомним свойство логарифма
x→ x0
eln f (x ) g (x ) = f (x)g (x ) .
1
Пример. Найти limx→0(cos2x) x2 .
14
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дифференциалом порядка n, где n > 1 от функции 
.
Дифференциал высшего порядка функции одной переменной
Для функции, зависящей от одной переменной 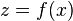
Отсюда можно вывести общий вид дифференциала n-го порядка от функции 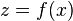
При вычислении дифференциалов высших порядков очень важно, что 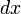


Дифференциал высшего порядка функции нескольких переменных
Если функция 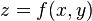
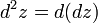
Символически общий вид дифференциала n-го порядка от функции 
где 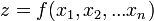
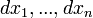
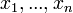
Приращения 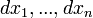
Неинвариантность дифференциалов высшего порядка
При 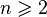

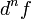


Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
При n = 2 и 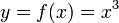
С учётом зависимости 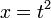
Дополнения
- С помощью дифференциалов, функция
при условии существования её (n + 1) первых производных может быть представлена по формуле Тейлора:
-
- для функции с одной переменной:
,
;
- для функции с несколькими переменными:
,
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Дифференциалы высших порядков
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Пусть дана функция y = f(x), где х – независимая переменная. Дифференциал этой функции есть некоторая функция от х, но от х зависит только первый сомножитель f ‘(x) второй же сомножитель dx является приращением независимой переменной x и от значения этой переменной не зависит.
$dy = f ‘(x)dx$
Функция dy есть функция от x и называется дифференциалом.
Что такое дифференциал второго, третьего и n-го порядка функции
Определение
Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается $d^2y$.
$d^2y = d(dy)$
Определение
Третьим дифференциалом или дифференциалом третьего порядка функции называется~дифференциал~от ее второго дифференциала:
$d^3y = d(d^2y) = f ”'(x)dx^3$
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение
Дифференциалом n-го порядка является дифференциал от дифференциала (n-1)-го порядка:
$d^ny = d(d^{n-1}y)$
Пример 1
Найти дифференциал третьего порядка функции.
[y(x)=x^{4} +2arccos x]
Решение.
- По определению дифференциала, дифференциал 3 порядка равен:
[d^{3} y=y”'(x)dx^{3} ]
- Продифференцируем данную функцию по х:
- Вычислим вторую производную
- Вычислим третью производную
- Подставим полученную производную в формулу дифференциала второго порядка:
[y'(x)=(x^{4} +2arccos x)’=(x^{4} )’+2(arccos x)’=4x^{3} -frac{2}{sqrt{1-x^{2} } } ]
[y”(x)=left(4x^{3} -frac{2}{sqrt{1-x^{2} } } right)^{{‘} } =12x^{2} -2left((1-x^{2} )^{-frac{1}{2} } right)^{{‘} } =12x^{2} -2frac{1}{2} (1-x^{2} )^{-frac{3}{2} } (1-x^{2} )’]
[y”(x)=12x^{2} -2x(1-x^{2} )^{-frac{3}{2} } ]
[y”'(x)=left(12x^{2} -2x(1-x^{2} )^{-frac{3}{2} } right)^{{‘} } =24x-left(2(1-x^{2} )^{-frac{3}{2} } +2xleft((1-x^{2} )^{-frac{1}{2} } right)^{{‘} } right)]
[y”'(x)=left(12x^{2} -2x(1-x^{2} )^{-frac{3}{2} } right)^{{‘} } =24x-2(1-x^{2} )^{-frac{3}{2} } -4frac{3}{2} x^{2} (1-x^{2} )^{-frac{5}{2} } ]
[y”'(x)=24x-frac{2}{sqrt{(1-x^{2} )^{3} } } -frac{6x^{2} }{sqrt{(1-x^{2} )^{5} } } ]
[d^{3} y=y”'(x)dx^{3} =left(24x-frac{2}{sqrt{(1-x^{2} )^{3} } } -frac{6x^{2} }{sqrt{(1-x^{2} )^{5} } } right)dx^{3} ]
«Дифференциалы высших порядков» 👇
Пример 2
Найти дифференциал 4 порядка функции.
[y(x)=e^{4x} sin 3x]
Решение.
- Запишем производную по формуле Лейбница
- Посчитаем коэффициенты при слагаемых
- Найдем производные первого сомножителя
- Найдем производные второго сомножителя
- Подставим найденные значения в формулу Лейбница
- Упростим
- Формула дифференциала 4 порядка имеет вид:
[y^{(4)} (x)=left(e^{4x} right)^{(4)} sin 3x+C_{4}^{1} left(e^{4x} right)^{(3)} sin 3x’+C_{4}^{2} left(e^{4x} right)^{(2)} sin 3x”+C_{4}^{3} left(e^{4x} right){{‘} } sin 3x”’+e^{4x} sin 3x^{(4)} ]
[C_{4}^{1} =frac{4!}{1!(4-1)!} =frac{4!}{3!} =frac{3!4}{3!} =4]
[C_{4}^{2} =frac{4!}{2!(4-2)!} =frac{4!}{2!2!} =frac{1cdot 2cdot 3cdot 4}{1cdot 2cdot 1cdot 2} =6]
[C_{4}^{3} =frac{4!}{3!(4-3)!} =frac{4!}{3!1!} =frac{3!4}{3!} =4]
[left(e^{4x} right){{‘} } =e^{4x} cdot 4x’=4e^{4x} ]
[left(e^{4x} right){{‘} } {{‘} } =left(4e^{4x} right){{‘} } =16e^{4x} ]
[left(e^{4x} right){{‘} } {{‘} } {{‘} } =left(16e^{4x} right){{‘} } =64e^{4x} ]
[left(e^{4x} right)^{(4)} =left(64e^{4x} right){{‘} } {{‘} } {{‘} } =256e^{4x} ]
[sin 3x’=cos 3xcdot 3x’=3cos 3x]
[sin 3x”=left(3cos 3xright){{‘} } =3left(-sin 3xright)cdot left(3xright){{‘} } =-9sin 3x]
[sin 3x”’=left(-9sin 3xright){{‘} } ^{} =-27cos 3x]
[sin 3x^{(4)} =left(-27cos 3xright){{‘} } =81sin 3x]
[y^{(4)} (x)=256e^{4x} sin 3x+4cdot 64e^{4x} cdot 3cos 3x+6cdot 16e^{4x} cdot left(-9sin 3xright)+4cdot 4e^{4x} cdot left(-27cos 3xright)+e^{4x} cdot 81sin 3x]
[y^{(4)} (x)=e^{4x} (336cos 3x-527sin 3x)]
[d^{left(4right)} y=y^{(4)} (x)dx^{4} ]
[d^{left(4right)} y=e^{4x} (336cos 3x-527sin 3x)dx^{4} ]
Пример 3
Найти дифференциал 3 порядка функции
[y=5^{2x-5} ]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(a^{kx+b} right)^{(n)} =k^{n} a^{kx+b} ln ^{n} a]
Где $k = 2, b = -5, a = 5, n = 3$
[y^{(3)} =left(5^{2x-5} right)^{(3)} =2^{3} cdot 5^{2x-5} cdot ln ^{3} 5]
[y^{(3)} =2^{3} cdot 5^{2x-5} cdot ln ^{3} 5=frac{8cdot 25^{x} }{3125} ln ^{3} 5]
Формула дифференциала 3 порядка имеет вид:
[d^{left(3right)} y=y^{(3)} (x)dx^{3} ]
[d^{left(3right)} y=frac{8cdot 25^{x} }{3125} ln ^{3} 5dx^{3} ]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.12.2022















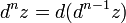 .
.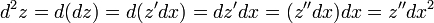
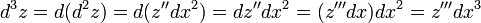
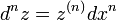
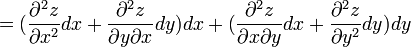
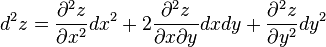
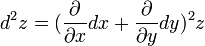
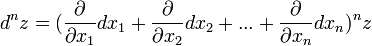
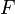 при условии существования её
при условии существования её ,
,  ;
;
 ,
, 
