
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
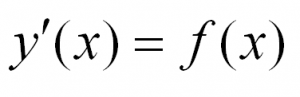
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
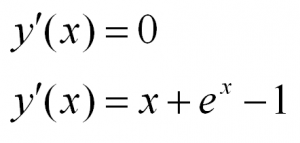
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
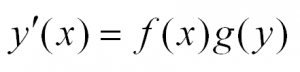
Приведем пример:
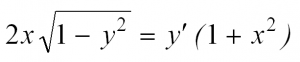
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
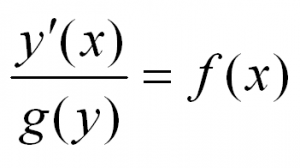
После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
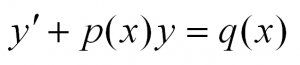
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
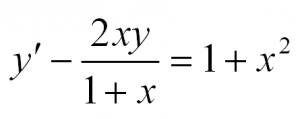
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
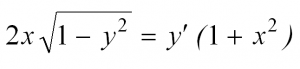
Сначала перепишем производную в более привычном виде:
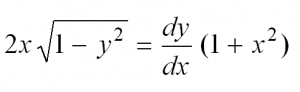
Затем разделим переменные, то есть в одной части уравнения соберем все “игреки”, а в другой – “иксы”:
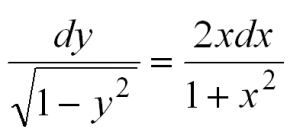
Теперь осталось проинтегрировать обе части:
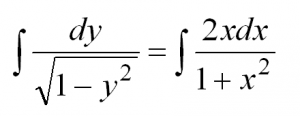
Интегрируем и получаем общее решение данного уравнения:
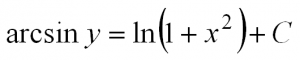
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему “Как решать дифференциальные уравнения”:
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.
Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} – 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} – 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t – 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = – int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$ |
| Ответ |
| $$y = x^4 – x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x – cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y”)=0$
- Без переменной $x$: $F(y,y’,y”)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Помощь в написании работы
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
То есть,
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
y=Cx, где С=Const.
Задание
Найти частное решение дифференциального уравнения
.
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
где С=const.
Ответ
где С=const.
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Общий интеграл:
где С=const.
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
где С=const
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Частное решение:
.
Задание
Решить дифференциальное уравнение
.
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Общий интеграл:
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Интегрируем:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
Используя
можно выразить функцию в явном виде.
Общее решение:
где С=const.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Частное решение:
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
0=0
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Общий интеграл:
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Интегрируем:
Общий интеграл:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Частный интеграл:
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
Таким образом:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Обратная замена:
Ответ
Общий интеграл:
где С=const.
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Ответ
Общее решение:
где С=const.
Загрузить PDF
Загрузить PDF
Дифференциальное уравнение — это уравнение, в которое входят функция и одна или несколько ее производных. В большинстве практических задач функции представляют собой физические величины, производные соответствуют скоростям изменения этих величин, а уравнение определяет связь между ними.
В данной статье рассмотрены методы решения некоторых типов обыкновенных дифференциальных уравнений, решения которых могут быть записаны в виде элементарных функций, то есть полиномиальных, экспоненциальных, логарифмических и тригонометрических, а также обратных им функций. Многие из этих уравнений встречаются в реальной жизни, хотя большинство других дифференциальных уравнений нельзя решить данными методами, и для них ответ записывается в виде специальных функций или степенных рядов, либо находится численными методами.
Для понимания данной статьи необходимо владеть дифференциальным и интегральным исчислением, а также иметь некоторое представление о частных производных. Рекомендуется также знать основы линейной алгебры в применении к дифференциальным уравнениям, особенно к дифференциальным уравнениям второго порядка, хотя для их решения достаточно знания дифференциального и интегрального исчисления.
Предварительные сведения
- Дифференциальные уравнения имеют обширную классификацию. В настоящей статье рассказывается об обыкновенных дифференциальных уравнениях, то есть об уравнениях, в которые входит функция одной переменной и ее производные. Обыкновенные дифференциальные уравнения намного легче понять и решить, чем дифференциальные уравнения в частных производных, в которые входят функции нескольких переменных. В данной статье не рассматриваются дифференциальные уравнения в частных производных, поскольку методы решения этих уравнений обычно определяются их конкретным видом.
-
Порядок дифференциального уравнения определяется по порядку старшей производной, входящей в данное уравнение. Первое из приведенных выше обыкновенных дифференциальных уравнений имеет первый порядок, в то время как второе относится к уравнениям второго порядка. Степенью дифференциального уравнения называется наивысшая степень, в которую возводится один из членов этого уравнения.
- Например, приведенное ниже уравнение имеет третий порядок и вторую степень.
- Например, приведенное ниже уравнение имеет третий порядок и вторую степень.
- Дифференциальное уравнение является линейным дифференциальным уравнением в том случае, если функция и все ее производные стоят в первой степени. В противном случае уравнение является нелинейным дифференциальным уравнением. Линейные дифференциальные уравнения примечательны тем, что из их решений можно составить линейные комбинации, которые также будут решениями данного уравнения.
-
Общее решение обыкновенного дифференциального уравнения не является единственным, оно включает в себя произвольные постоянные интегрирования. В большинстве случаев число произвольных постоянных равно порядку уравнения. На практике значения этих констант определяются по заданным начальным условиям, то есть по значениям функции и ее производных при
Число начальных условий, которые необходимы для нахождения частного решения дифференциального уравнения, в большинстве случаев также равно порядку данного уравнения.
-
1
Линейные уравнения первого порядка. В данном разделе рассмотрены методы решения линейных дифференциальных уравнений первого порядка в общих и специальных случаях, когда некоторые члены равны нулю. Предположим, что
и
являются функциями
Согласно одной из основных теорем математического анализа, интеграл от производной функции также является функцией. Таким образом, достаточно просто проинтегрировать уравнение, чтобы найти его решение. При этом следует учесть, что при вычислении неопределенного интеграла появляется произвольная постоянная.
Используем метод разделения переменных. При этом различные переменные переносятся в разные стороны уравнения. Например, можно перенести все члены с
в одну, а все члены с
в другую сторону уравнения. Можно переносить также члены
и
, которые входят в выражения производных, однако следует помнить, что это всего лишь условное обозначение, которое удобно при дифференцировании сложной функции. Обсуждение этих членов, которые называются дифференциалами, выходит за рамки данной статьи.
Для нахождения общего решения мы ввели интегрирующий множитель
в виде функции от
, чтобы свести левую часть к общей производной и таким образом решить уравнение.
Решение линейных уравнений первого порядка (запись Интуита – национального открытого университета).
-
2
Нелинейные уравнения первого порядка. В данном разделе рассмотрены методы решения некоторых нелинейных дифференциальных уравнений первого порядка. Хотя и не существует общего метода решения таких уравнений, некоторые из них можно решить с помощью приведенных ниже методов.
Если функцию
можно разделить на функции одной переменной, такое уравнение называется дифференциальным уравнением с разделяющимися переменными. В этом случае можно воспользоваться приведенным выше методом:
Предположим, что
и
являются функциями
и
Тогда однородным дифференциальным уравнением называется такое уравнение, в котором
и
являются однородными функциями одинаковой степени. То есть функции должны удовлетворять условию
где
называется степенью однородности. Любое однородное дифференциальное уравнение можно путем подходящей замены переменных (
или
) преобразовать в уравнение с разделяющимися переменными.
- Пример 1.4. Приведенное выше описание однородности может показаться неясным. Рассмотрим это понятие на примере.
Это дифференциальное уравнение Бернулли — особый вид нелинейного уравнения первой степени, решение которого может быть записано с помощью элементарных функций.
Это уравнение в полных дифференциалах. Необходимо найти так называемую потенциальную функцию
, которая удовлетворяет условию
- Для выполнения данного условия необходимо наличие полной производной. Полная производная учитывает зависимость от других переменных. Чтобы вычислить полную производную
по
мы предполагаем, что
может также зависеть от
- Сравнение слагаемых дает нам
и
Это типичный результат для уравнений с несколькими переменными, при котором смешанные производные гладких функций равны друг другу. Иногда такой случай называют теоремой Клеро. В этом случае дифференциальное уравнение является уравнением в полных дифференциалах, если выполняется следующее условие:
- Метод решения уравнений в полных дифференциалах аналогичен нахождению потенциальных функций при наличии нескольких производных, на чем мы кратко остановимся. Сначала проинтегрируем
по
Поскольку
является функцией и
, и
при интегрировании мы получим неполную функцию
обозначенную как
. В результат входит также зависящая от
постоянная интегрирования.
- После этого для получения
можно взять частную производную полученной функции по
приравнять результат
и проинтегрировать. Можно также сначала проинтегрировать
, а затем взять частную производную по
, что позволит найти произвольную функцию
Подходят оба метода, и обычно для интегрирования выбирается более простая функция.
-
Пример 1.5. Можно взять частные производные и убедиться в том, что приведенное ниже уравнение является уравнением в полных дифференциалах.
- Если дифференциальное уравнение не является уравнением в полных дифференциалах, в некоторых случаях можно найти интегрирующий множитель, который позволит преобразовать его в уравнение в полных дифференциалах. Однако подобные уравнения редко применяются на практике, и хотя интегрирующий множитель существует, найти его бывает непросто, поэтому эти уравнения не рассматриваются в данной статье.
Реклама
-
1
Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Эти уравнения широко используются на практике, поэтому их решение имеет первоочередное значение. В данном случае речь идет не об однородных функциях, а о том, что в правой части уравнения стоит 0. В следующем разделе будет показано, как решаются соответствующие неоднородные дифференциальные уравнения. Ниже
и
являются константами.
Характеристическое уравнение. Данное дифференциальное уравнение примечательно тем, что его можно очень легко решить, если обратить внимание на то, какими свойствами должны обладать его решения. Из уравнения видно, что
и его производные пропорциональны друг другу. Из предыдущих примеров, которые были рассмотрены в разделе об уравнениях первого порядка, мы знаем, что таким свойством обладает лишь экспоненциальная функция. Следовательно, можно выдвинуть анзац (обоснованное предположение) о том, каким будет решение данного уравнения.
- Решение будет иметь вид экспоненциальной функции
где
— постоянная, значение которой следует найти. Подставим эту функцию в уравнение и получим следующее выражение
- Это уравнение свидетельствует о том, что произведение экспоненциальной функции и полинома должно равняться нулю. Известно, что экспонента не может равняться нулю ни при каких значениях степени. Отсюда заключаем, что нулю равен полином. Таким образом, мы свели задачу решения дифференциального уравнения к намного более простой задаче решения алгебраического уравнения, которое называется характеристическим уравнением для данного дифференциального уравнения.
- Мы получили два корня. Поскольку данное дифференциальное уравнение является линейным, его общее решение представляет собой линейную комбинацию частных решений. Так как это уравнение второго порядка, мы знаем, что это действительно общее решение, и других не существует. Более строгое обоснование этого заключается в теоремах о существовании и единственности решения, которые можно найти в учебниках.
- Полезный способ проверить, являются ли два решения линейно независимыми, заключается в вычислении вронскиана. Вронскиан
— это определитель матрицы, в колонках которой стоят функции и их последовательные производные. Теорема линейной алгебры гласит, что входящие в вронскиан функции линейно зависимы, если вронскиан равен нулю. В данном разделе мы можем проверить, являются ли два решения линейно независимыми — для этого необходимо убедиться, что вронскиан не равен нулю. Вронскиан важен при решении неоднородных дифференциальных уравнений с постоянными коэффициентами методом вариации параметров.
- В терминах линейной алгебры множество всех решений данного дифференциального уравнения образует векторное пространство, размерность которого равна порядку дифференциального уравнения. В этом пространстве можно выбрать базис из линейно независимых друг от друга решений. Это возможно благодаря тому, что на функцию
действует линейный оператор. Производная является линейным оператором, поскольку она преобразует пространство дифференцируемых функций в пространство всех функций. Уравнения называются однородными в тех случаях, когда для какого-либо линейного оператора
требуется найти решение уравнения
Перейдем теперь к рассмотрению нескольких конкретных примеров. Случай кратных корней характеристического уравнения рассмотрим чуть позже, в разделе о понижении порядка.
Два различных действительных корня. Если корни
являются различными действительными числами, дифференциальное уравнение имеет следующее решение
Два комплексных корня. Из основной теоремы алгебры следует, что решения решения полиномиальных уравнений с действительными коэффициентами имеют корни, которые вещественны или образуют сопряженные пары. Следовательно, если комплексное число
является корнем характеристического уравнения, тогда
также является корнем этого уравнения. Таким образом, можно записать решение в виде
однако это комплексное число, и оно нежелательно при решении практических задач.
Решение дифференциальных уравнений n-го порядка с постоянными коэффициентами (запись Интуита – национального открытого университета).
- Решение будет иметь вид экспоненциальной функции
-
2
Понижение порядка. Понижение порядка представляет собой метод решения дифференциальных уравнений в случае, когда известно одно линейно независимое решение. Данный метод заключается в понижении порядка уравнения на один, что позволяет решить уравнение методами, которые описаны в предыдущем разделе. Пусть известно решение
. Основная идея понижения порядка заключается в поиске решения в представленном ниже виде, где необходимо определить функцию
, подстановке его в дифференциальное уравнение и нахождении
Рассмотрим, как можно использовать понижение порядка для решения дифференциального уравнения с постоянными коэффициентами и кратными корнями.
Кратные корни однородного дифференциального уравнения с постоянными коэффициентами. Вспомним о том, что уравнение второго порядка должно иметь два линейно независимых решения. Если характеристическое уравнение имеет кратные корни, множество решений не образует пространство, поскольку эти решения линейно зависимы. В этом случае необходимо использовать понижение порядка, чтобы найти второе линейно независимое решение.
Понижение порядка применимо в том случае, если известно решение
, которое может быть найдено или дано в условии задачи.
-
3
Уравнение Коши-Эйлера. Уравнение Коши-Эйлера является примером дифференциального уравнения второго порядка с переменными коэффициентами, которое имеет точные решения. Это уравнение применяется на практике, например для решения уравнения Лапласа в сферических координатах.
Характеристическое уравнение. Как видно, в данном дифференциальном уравнении каждый член содержит степенной множитель, степень которого равна порядку соответствующей производной.
Два различных действительных корня. Если корни
действительны и различны, тогда решение дифференциального уравнения имеет следующий вид:
Два комплексных корня. Если характеристическое уравнение имеет корни
, решением является комплексная функция.
Кратные корни. Чтобы получить второе линейно независимое решение, необходимо вновь провести понижение порядка.
-
4
Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами. Неоднородные уравнения имеют вид
где
— так называемый свободный член. Согласно теории дифференциальных уравнений, общее решение данного уравнения представляет собой суперпозицию частного решения
и дополнительного решения
Однако в данном случае частное решение означает не решение, заданное начальными условиями, а скорее такое решение, которое обусловлено наличием неоднородности (свободным членом). Дополнительное решение — это решение соответствующего однородного уравнения, в котором
Общее решение представляет собой суперпозицию этих двух решений, поскольку
, а так как
такая суперпозиция действительно является общим решением.
Метод неопределенных коэффициентов. Метод неопределенных коэффициентов применяется в тех случаях, когда свободный член представляет собой комбинацию экспоненциальных, тригонометрических, гиперболических или степенных функций. Лишь эти функции гарантированно имеют конечное число линейно независимых производных. В данном разделе мы найдем частное решение уравнения.
Метод Лагранжа. Метод Лагранжа, или метод вариации произвольных постоянных, представляет собой более общий метод решения неоднородных дифференциальных уравнений, особенно в тех случаях, когда свободный член не содержит конечное число линейно независимых производных. Например, при свободных членах
или
для нахождения частного решения необходимо использовать метод Лагранжа. Метод Лагранжа можно даже использовать для решения дифференциальных уравнений с переменными коэффициентами, хотя в этом случае, за исключением уравнения Коши-Эйлера, он применяется реже, поскольку дополнительное решение обычно не выражается через элементарные функции.
Лекция национального открытого университета Интуит под названием “Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами”.
Реклама
Практическое применение
Дифференциальные уравнения устанавливают связь между функцией и одной или несколькими ее производными. Поскольку подобные связи чрезвычайно распространены, дифференциальные уравнения нашли широкое применение в самых разных сферах, а так как мы живем в четырех измерениях, эти уравнения часто представляют собой дифференциальные уравнения в частных производных. В данном разделе рассмотрены некоторые из наиболее важных уравнений этого типа.
-
Экспоненциальный рост и распад. Радиоактивный распад. Составные проценты. Скорость химических реакций. Концентрация лекарств в крови. Неограниченный рост популяции. Закон Ньютона-Рихмана. В реальном мире существует множество систем, в которых скорость роста или распада в любой момент времени пропорциональна количеству в данный момент времени или может быть хорошо аппроксимирована моделью. Это объясняется тем, что решение данного дифференциального уравнения, экспоненциальная функция, является одной из наиболее важных функций в математике и других науках. В более общем случае при контролируемом росте популяции система может включать дополнительные члены, которые ограничивают рост. В приведенном ниже уравнении постоянная
может быть как больше, так и меньше нуля.
-
Гармонические колебания. И в классической, и в квантовой механике гармонический осциллятор является одной из наиболее важных физических систем благодаря своей простоте и широкому применению для аппроксимации более сложных систем, таких как простой маятник. В классической механике гармонические колебания описываются уравнением, которое связывает положение материальной точки с ее ускорением посредством закона Гука. При этом можно учитывать также демпфирующие и движущие силы. В приведенном ниже выражении
— производная по времени от
— параметр, который описывает демпфирующую силу,
— угловая частота системы,
— зависящая от времени движущая сила. Гармонический осциллятор присутствует также в электромагнитных колебательных контурах, где его можно реализовать с большей точностью, чем в механических системах.
-
Уравнение Бесселя. Дифференциальное уравнение Бесселя используется во многих областях физики, в том числе для решения волнового уравнения, уравнения Лапласа и уравнения Шредингера, особенно при наличии цилиндрической или сферической симметрии. Это дифференциальное уравнение второго порядка с переменными коэффициентами не является уравнением Коши-Эйлера, поэтому его решения не могут быть записаны в виде элементарных функций. Решениями уравнения Бесселя являются функции Бесселя, которые хорошо изучены благодаря тому, что применяются во многих областях. В выражении ниже
— константа, которая соответствует порядку функции Бесселя.
-
Уравнения Максвелла. Наряду с силой Лоренца уравнения Максвелла составляют основу классической электродинамики. Это четыре дифференциальных уравнения в частных производных для электрического
и магнитного
поля. В приведенных ниже выражениях
— плотность заряда,
— плотность тока, а
и
— соответственно электрическая и магнитная постоянные.
-
Уравнение Шредингера. В квантовой механике уравнение Шредингера является основным уравнением движения, которое описывает перемещение частиц в соответствии с изменением волновой функции
со временем. Уравнение движения описывается поведением гамильтониана
— оператора, который описывает энергию системы. Одним из широко известных примеров уравнения Шредингера в физике является уравнение для одной нерелятивистской частицы, на которую действует потенциал
. Многие системы описываются зависящим от времени уравнением Шредингера, при этом в левой части уравнения стоит
где
— энергия частицы. В выражениях ниже
— приведенная постоянная Планка.
-
Волновое уравнение. Без волн нельзя представить физику и технику, они присутствуют во всех типах систем. В общем случае волны описываются приведенным ниже уравнением, в котором
является искомой функцией, а
— экспериментально определяемая постоянная. Даламбер был первым, кто обнаружил, что для одномерного случая решением волнового уравнения является любая функция с аргументом
, которая описывает волну произвольной формы, распространяющуюся вправо. Общее решение для одномерного случая представляет собой линейную комбинацию этой функции со второй функцией с аргументом
, которая описывает волну, распространяющуюся влево. Это решение представлено во второй строке.
-
Уравнения Навье-Стокса. Уравнения Навье-Стокса описывают движение жидкостей. Поскольку жидкости присутствуют практически в каждой области науки и техники, эти уравнения чрезвычайно важны для предсказания погоды, конструирования самолетов, изучения океанских течений и решения множества других прикладных задач. Уравнения Навье-Стокса являются нелинейными дифференциальными уравнениями в частных производных, и в большинстве случаев решить их очень сложно, поскольку нелинейность приводит к турбулентности, и для получения устойчивого решения численными методами необходимо разбиение на очень мелкие ячейки, что требует значительных вычислительных мощностей. Для практических целей в гидродинамике для моделирования турбулентных потоков используют такие методы, как усреднение по времени. Сложными задачами являются даже более основные вопросы, такие как существование и единственность решений для нелинейных уравнений в частных производных, а доказательство существования и единственности решения для уравнений Навье-Стокса в трех измерениях входит в число математических задач тысячелетия. Ниже приведены уравнение потока несжимаемой жидкости и уравнение непрерывности.
Советы
- Многие дифференциальные уравнения просто невозможно решить приведенными выше методами, особенно упомянутые в последнем разделе. Это касается тех случаев, когда уравнение содержит переменные коэффициенты и не является уравнением Коши-Эйлера, или когда уравнение является нелинейным, за исключением нескольких очень редких случаев. Тем не менее, приведенные выше методы позволяют решить многие важные дифференциальные уравнения, которые часто встречаются в различных областях науки.
- В отличие от дифференцирования, которое позволяет найти производную любой функции, интеграл многих выражений нельзя выразить в элементарных функциях. Поэтому не тратьте время в попытках вычислить интеграл там, где это невозможно. Загляните в таблицу интегралов. Если решение дифференциального уравнения нельзя выразить через элементарные функции, иногда его можно представить в интегральной форме, и в данном случае неважно, можно ли вычислить данный интеграл аналитически.
Реклама
Предупреждения
Об этой статье
Эту страницу просматривали 102 152 раза.



















![L[y]=0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a221ef170dfec343b59061cb9d09090f52d02a4)














