Как найти дифферент судна

Продольная остойчивость отличается от поперечной остойчивости, так как она не делится на начальную и остойчивость при больших углах дифферента, потому что больших углов дифферента в принципе не может быть из-за значительной длины судов.

Понятие о продольной остойчивости судна

Остойчивость, которая проявляется при продольных наклонениях судна, т. е. при дифференте, называется продольной.

Несмотря на то, что углы дифферента судна редко достигают 10 град, а обычно составляют 2–3 град, продольное наклонение приводит к значительным линейным дифферентам при большой длине судна. Так, у судна длиной 150 м угол наклонения 1° соответствует линейному дифференту, равному 2,67 м. В связи с этим в практике эксплуатации судов вопросы, относящиеся к дифференту, более важны, чем вопросы продольной остойчивости, поскольку у транспортных судов с нормальными соотношениями главных размеренийОпределение главных размерений и водоизмещения буксирных судов продольная остойчивость всегда положительна.

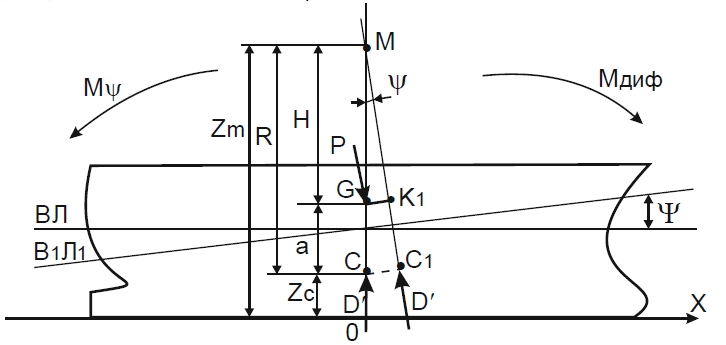
При продольном наклонении судна на угол Ψ вокруг поперечной оси Ц.В. переместится из точки С в точку С1 и сила поддержания, направление которой нормально к действующей ватерлинии, будет действовать под углом Ψ к первоначальному направлению. Линии действия первоначального и нового направлении сил поддержания пересекаются в точке. Точка пересечения линии действия сил поддержания при бесконечно малом наклонении в продольной плоскости называется продольным метацентром M.

Предлагается к прочтению: Диаграмма остойчивости и диаграмма динамической остойчивости (ДДО)

Радиус кривизны кривой перемещения Ц.В. в продольной плоскости называется продольным метацентрическим радиусом R, который определяется расстоянием от продольного метацентра до Ц.В.

Формула для вычисления продольного метацентрического радиуса R аналогична поперечному метацентрическому радиусу:

R = IF/V,

где:

• I_F – момент инерции площади ватерлинии относительно поперечной оси, проходящей через ее Ц.Т. (точка F);
• V – объемное водоизмещение судна.

Продольный момент инерции площади ватерлинии I_F значительно больше поперечного момента инерции I_X. Поэтому продольный метацентрический радиус R всегда значительно больше поперечного r. Ориентировочно считают, что продольный метацентрический радиус R приблизительно равен длине судна.

Основное положение остойчивости заключается в том, что восстанавливающий момент является моментом пары, образованной силой веса судна и силой поддержания. Как видно из рисунка в результате приложения действующего в ДП внешнего момента, называемого дифферентующим моментом M_диф, судно получило наклонение на малый угол дифферента Ψ. Одновременно с появлением угла дифферента возникает восстанавливающий момент MΨ, действующий в сторону, противоположную действию дифферентующего момента.

Продольное наклонение судна будет продолжаться до тех пор, пока алгебраическая сумма обоих моментов не станет равной нулю. Поскольку оба момента действуют в противоположные стороны, условие равновесия можно записать в виде равенства:

Mдиф=MΨ

Восстанавливающий момент в этом случае будет:

MΨ=D′·GK1          Форм. 1

где:

• GK1 – плечо этого момента, называемое плечом продольной остойчивости.

Из прямоугольного треугольника G M K1 получаем:

GK1=MG·sinΨ=H sinΨ          Форм. 2

Входящая в последнее выражение величина MG = H определяет возвышение продольного метацентра над Ц.Т. судна и называется продольной метацентрической высотой. Подставив выражение (Формула 2) в формулу 1, получим:

MΨ=D′·H·sin Ψ          Форм. 3

Где произведение D′H – коэффициент продольной остойчивости. Имея в виду, что продольная метацентрическая высота Н = R – a, формулу 3 можно записать в виде:

MΨ=D‘·(R–а)·sin Ψ          Форм. 4

где:

• a – возвышение Ц.Т. судна над его Ц.В.

Формулы 3 и 4 являются метацентрическими формулами продольной остойчивости. Ввиду малости угла дифферента в указанных формулах, вместо sinΨ можно подставить угол Ψ (в радианах) и тогда:

MΨ=D′·H·Ψ     или     MΨ=D′·(R–а)·Ψ.

Поскольку величина продольного метацентрического радиуса R во много раз больше поперечного r, продольная метацентрическая высота H любого судна во много раз больше поперечной h, поэтому, если у судна обеспечена поперечная остойчивость, то продольная остойчивость обеспечена заведомо.

Дифферент судна и угол дифферента

В практике расчетов наклонений судна в продольной плоскости, связанных с определением дифферента, вместо углового дифферента принято пользоваться линейным дифферентом, значение которого определяется как разность осадок судна носом и кормой, т. е. d = T_H – T_K.

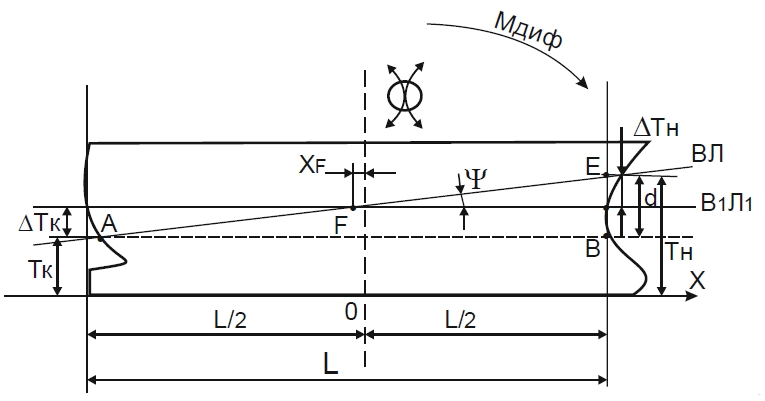
Дифферент принято считать положительным, если осадка судна носом больше, чем кормой; дифферент на корму считается отрицательным. В большинстве случаев суда плавают с дифферентом на корму. Предположим, что судно, плавающее на ровный киль по ватерлинию ВЛ, под действием некоторого момента получило дифферент и его новая действующая ватерлиния заняла положение В₁Л₁. Из формулы для восстанавливающего момента имеем:

Ψ=MΨD′·H

Проведем пунктирную линию АВ, параллельную ВЛ, через точку пересечения кормового перпендикуляра с В₁Л₁. Дифферент d – определяется катетом ВЕ треугольника ABE. Отсюда:

tg Ψ=Ψ=d/L

Сравнив последние два выражения, получим:

dL=MΨD′·H,     отсюда     MΨ=dL·D′·H

Изменение дифферента при продольном перемещении груза

Рассмотрим методы определения осадок судна при действии на него дифферентующего момента, возникающего в результате перемещения груза в продольно-горизонтальном направлении.

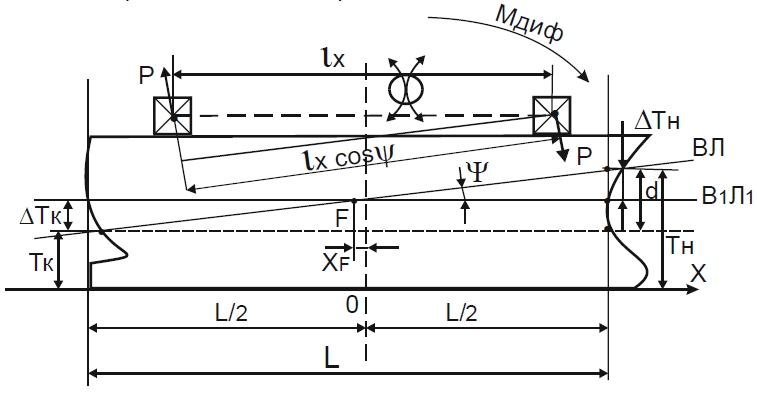
Допустим, что груз весом P перемещен вдоль судна на расстояние ιx. Перемещение груза, как уже указывалось, может быть заменено приложением к судну момента пары сил. В нашем случае этот момент будет дифферентующим и равным: M_диф = P · l_X · cosΨ. Уравнение равновесия при продольном перемещении груза (равенство дифферентующего и восстанавливающего моментов) имеет вид:

p·lx·cosΨ=D′·H·sinΨ

• откуда:

tgψ=P·IXD′·H

Поскольку малые наклонения судна происходят вокруг оси, проходящей через Ц.Т. площади ватерлинии (т. F), можно получить следующие выражения для изменения осадок носом и кормой:

∆TH=(L2–XF)·tg ψ=P·IXD′·H·(L2–XF)

∆TH=(L2+XF)·tg ψ=–P·IXD′·H·(L2+XF)

Следовательно, осадки носом и кормой при перемещении груза вдоль судна будут:

Tн=T+∆Tн=T+P·IxD′·H·(L2–XF)

Tк=T+∆Tк=T+P·IxD′·H·(L2–XF)

Если учесть, что tg Ψ = d/L и что D′ · H · sin Ψ = MΨ, можно записать:

Tн=T+P·Ix100·M1см·(12–XFL)

Tк=T–P·Ix100·M1см·(12+XFL)

где:

• T – осадка судна при положении на ровный киль;
• M_1см – момент, дифферентующий судно на 1 см.

Значение абсциссы X_F находят по “кривым элементов теоретического чертежа”, причем необходимо строго учитывать знак перед X_F: при расположении точки F в нос от миделя величина X_F считается положительной, а при расположении точки F в корму от миделя – отрицательной.

Плечо l_X также считается положительным, если груз переносится по направлению к носовой части судна; при переносе груза в корму плечо l_X считается отрицательным.

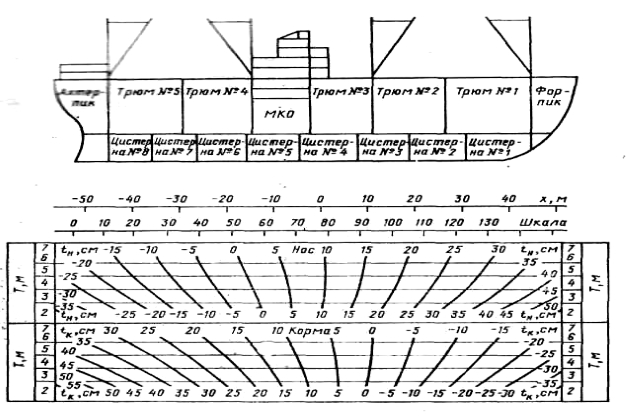
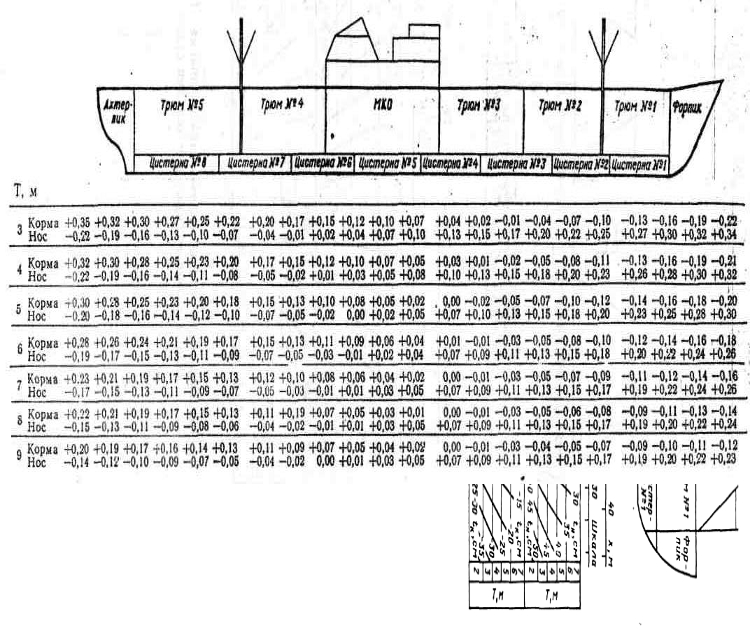
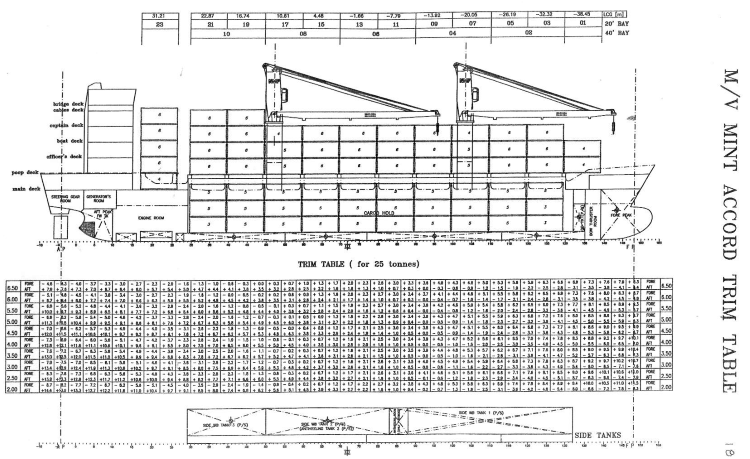
Шкала изменений осадки оконечностей вследствие приема 100 тонн груза

Наибольшее распространение получили шкалы и таблицы изменения осадок носом и кормой от приема единичного груза, масса которого в зависимости от водоизмещения выбирается равной 10, 25, 50, 100, 1 000 тонн. В основе построения такого рода шкал и таблиц лежат следующие соображения. Изменение осадки оконечностей судна при приеме груза слагается из увеличения средней осадки на величину ΔТ и изменения осадок оконечностей ΔT_H и ΔT_K. Величина ΔT не зависит от местоположения принятого груза, а значения ΔT_H и ΔT_K при данной осадке и фиксированной массе груза P будут изменяться пропорционально абсциссе Ц.Т. принятого груза Xp. Поэтому, используя такую зависимость, достаточно вычислить изменения осадок оконечностей от приема груза сначала в районе носового, а затем кормового перпендикуляров и построить шкалу или таблицу изменения осадок оконечностей судна от приема груза массой, например, 100 т. Значения ΔT, ΔT_H, ΔT_K вычисляются по формулам.

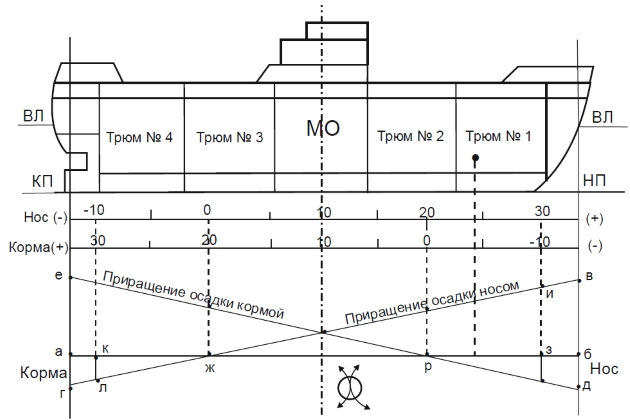
По полученным приращениям осадок оконечностей судна строим график изменений этих осадок от приема указанного груза.

Для этого на прямой а-б намечаем положение мидель – шпангоута и откладываем в выбранном масштабе вправо (в нос) и влево (в корму) половину длины судна. Из полученных точек восстанавливаем перпендикуляры к линии а-б. На носовом перпендикуляре откладываем вверх отрезок б-в, изображающий в выбранном масштабе вычисленное изменение осадки носом при приеме груза в носу. Аналогично на кормовом перпендикуляре откладываем вниз отрезок а-г, изображающий вычисленное изменение осадки носом при приеме груза в корму. Соединив прямой точки в-г, получаем график изменения осадки носом от приема груза массой 100 тонн.

ΔTн=+24 см=0,24 м;

ΔTк=+4 см=0,04 м

Таким же образом производится построение графика изменения осадки судна кормой от приема груза. Здесь отрезок б-д в принятом масштабе изображает изменение осадки кормой при приеме груза 100 т в носу, а отрезок а-е – при приеме груза в корму.

Производим градуировку шкал. Над графиком (или под ним) проводим две прямые линии для нанесения шкал изменения осадок: верхнюю – для носа, и нижнюю – для кормы. На каждой из них отмечаем точки, соответствующие делениям 0 (их положение определяется точками пересечения линии а-б с графиками в-г и е-д , т. е. точками ж-р). Затем между линией а-б и графиками в-г и е-д подбираем такие отрезки, длина которых в принятом масштабе была бы равна 30 или 10 см изменения осадки. Такими отрезками при градуировке шкалы “нос” будут отрезки з-и и к-л. В результате получим на шкале деления 30 и 10. Расстояния между 0 и 10, 10 и 20 делим на 10 равных частей. Размеры этих делений на обоих участках шкалы должны получиться одинаковыми.

Будет интересно: Диаграмма статической остойчивости (ДСО) и ее свойства

Используя график е-д, аналогичным способом строим шкалу для осадок кормой. При практических расчетах строят несколько шкал изменения осадок оконечностей от приема 100 тонн груза. Чаще всего строят шкалы для трех осадок (водоизмещений): осадки порожнего судна, осадки судна с полным грузом и промежуточную.

Шкалы, диаграммы или таблицы изменения осадок оконечностей судна от приема единичного груза (например 100 тонн) могут иметь очень разный вид. Несколько таких примеров приводим ниже на рисунках 5-7.

Сноски