Как найти дифракционный максимум второго порядка

При перпендикулярном (нормальном) падении параллельного пучка монохроматического света на дифракционную решётку на экране в фокальной плоскости собирающей линзы, расположенной параллельно дифракционной решётке, наблюдается неоднородная картина распределения освещённости разных участков экрана (дифракционная картина).

Главные максимумы этой дифракционной картины удовлетворяют следующим условиям:

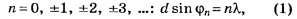
где n — порядок главного дифракционного максимума, d — постоянная (период) дифракционной решётки, λ— длина волны монохроматического света, φ_n— угол между нормалью к дифракционной решётке и направлением на главный дифракционный максимум n-го порядка.

Постоянная (период) дифракционной решётки длиной l

где N — количество щелей (штрихов), приходящихся на участок дифракционной решётки длиной I.

Наряду с длиной волны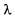часто используется частота v волны.

Для электромагнитных волн (света) в вакууме

где с = 3 *10⁸ м/с — скорость распространения света в вакууме. 

Выделим из формулы (1) наиболее трудно математически определяемые формулы для порядка главных дифракционных максимумов:

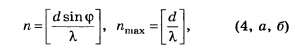
где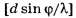 обозначает целую часть числа d*sin(φ/λ).

Недоопределённые аналоги формул (4, а,б) без символа […] в правых частях содержат в себе потенциальную опасность подмены физически обоснованной операции выделения целой части числа 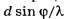операцией округления числа d*sin(φ/λ) до целочисленного значения по формальным математическим правилам.

Подсознательная тенденция (ложный след) подмены операции выделения целой части числа d*sin(φ/λ) операцией округления

этого числа до целочисленного значения по математическим правилам ещё более усиливается, когда речь идёт о тестовых заданиях типа В на определение порядка главных дифракционных максимумов.

В любых тестовых заданиях типа В численные значения искомых физических величин по договорённости округляются до целочисленных значений. Однако в математической литературе нет единых(го) правил(а) округления чисел.

В справочной книге В. А. Гусева, А. Г. Мордковича по математике для учащихся [1] и белорусском учебном пособии Л. А. Латотина, В. Я. Чеботаревского по математике для IV класса [2] приводятся по существу одни и те же два правила округления чисел. В [1] они сформулированы так: “При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяются нулями, а если стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1. Если же первая следующая за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют”.

В справочнике М. Я. Выгодского по элементарной математике [3], выдержавшем двадцать семь (!) изданий, написано (с. 74): “Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится до ближайшего чётного числа, т.е. последняя сохраняемая цифра остаётся неизменной, если она чётная, и усиливается (увеличивается на 1), если она нечётная”.

Ввиду существования различных правил округления чисел следовало бы правила округления десятичных чисел явно сформулировать в “Инструкции для учащихся”, прилагаемой к заданиям централизованного тестирования по физике. Это предложение приобретает дополнительную актуальность, так как в белорусские вузы поступают и проходят обязательное тестирование не только граждане Беларуси и России, но и других стран, и заведомо неизвестно, какими правилами округления чисел они пользовались при обучении в своих странах.

Во всех случаях округление десятичных чисел будем производить по правилам, приведённым в [1], [2].

После вынужденного отступления, возвратимся к обсуждению рассматриваемых физических вопросов.

С учётом нулевого (n = 0) главного максимума и симметричного расположения остальных главных максимумов относительно него общее количество наблюдаемых главных максимумов от дифракционной решётки подсчитывается по формулам:

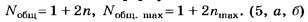
Если расстояние от дифракционной решётки до экрана, на котором наблюдается дифракционная картина, обозначить через Н, то координата главного дифракционного максимума n-го порядка при отсчёте от нулевого максимума равна

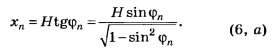
Если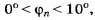 то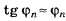 (радиан) 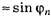и

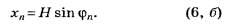
Задачи на рассматриваемую тему часто предлагают на тестированиях по физике.

Начнём обзор с рассмотрения российских тестов, использовавшихся белорусскими вузами на начальном этапе, когда тестирование в Беларуси было необязательным и проводилось отдельными учебными заведениями на свой страх и риск как альтернатива обычной индивидуальной письменно-устной форме проведения вступительных экзаменов.

Тест № 7 [4]

А32. Наибольший порядок спектра, который можно наблюдать при дифракции света с длиной волны λ на дифракционной решётке с периодом d=3,5λ равен

1) 4; 2) 7; 3) 2; 4) 8; 5) 3.

Решение

При освещении дифракционной решётки монохроматическим светом ни о каких спектрах не может быть и речи. В условии задачи речь должна идти о главном дифракционном максимуме наибольшего порядка при перпендикулярном падении монохроматического света на дифракционную решётку.

По формуле (4, б)

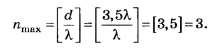
Из недоопределённого условия

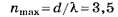
на множестве целых чисел, после округления получаем n_mах=4.

Только благодаря несовпадению целой части числа d/λ с его округлённым целочисленным значением правильное решение (n_mах=3) отличается от неправильного (n_max=4) на тестовом уровне.

Изумительная миниатюра, несмотря на огрехи формулировки, с филигранно выверенным по всем трём версиям округления чисел ложным следом!

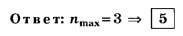
А18. Если постоянная дифракционной решётки d=2 мкм, то для нормально падающего на решётку белого света 400 нм <λ< 700 нм наибольший полностью наблюдаемый порядок спектра равен

1)1; 2)2; 3)3; 4)4; 5)5.

Решение

Очевидно, что n_сп=min(n_1max, n_2max)

По формуле (4, б)

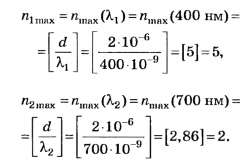
Округляя числа d/λ до целочисленных значений по правилам [1] — [3], получаем:

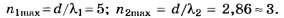
Благодаря тому, что целая часть числа d/λ₂ отличается от его округлённого целочисленного значения, данное задание позволяет на тестовом уровне объективно отличить правильное решение (n_сп=2) от неправильного (n_сп=3). Прекрасная задача с одним ложным следом!

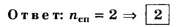
ЦТ 2002 г. Тест № 3 [5]

В5. Найдите наибольший порядок спектра для жёлтой линии Na (λ= 589 нм), если постоянная дифракционной решётки d = 2 мкм.

Решение

Задание сформулировано научно некорректно. Во-первых, при освещении дифракционной решётки монохроматическим светом, как уже отмечалось выше, не может быть и речи о спектре (спектрах). В условии задачи речь должна идти о наибольшем порядке главного дифракционного максимума.

Во-вторых, в условии задания должно быть указано, что свет падает нормально (перпендикулярно) на дифракционную решётку, ибо только этот частный случай рассматривается в курсе физики средних общеобразовательных учреждений. Считать это ограничение подразумевающимся по умолчанию нельзя: в тестах все ограничения должны быть указаны явно! Тестовые задания должны представлять собою самодостаточные, научно корректные задания.

С учётом вышеприведённых уточнений

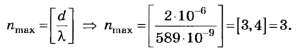
Число 3,4, округлённое до целочисленного значения по правилам арифметики [1] — [3], также даёт 3. Именно поэтому данное задание следует признать простым и, по большому счёту, неудачным, так как на тестовом уровне оно не позволяет объективно различить правильное решение, определяемое по целой части числа 3,4, от неправильного решения, определяемого по округлённому целочисленному значению числа 3,4. Различие обнаруживается только при подробном описании хода решения, что и сделано в данной статье.

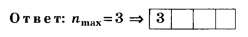
Дополнение 1. Решите вышеприведённую задачу, заменив в её условии d=2 мкм на d=1,6 мкм. Ответ: n_max = 2.

ЦТ 2002 г. Тест 4 [5]

В5. На дифракционную решётку направляется свет от газоразрядной лампы. На экране получаются дифракционные спектры излучения лампы. Линия с длиной волны λ₁= 510 нм в спектре четвёртого порядка совпадает с линией длины волны λ₂ в спектре третьего порядка. Чему равна λ₂(в [нм])?

Решение

В данной задаче основной интерес представляет не решение задачи, а формулировка её условия.

При освещении дифракционной решётки немонохроматическим светом(λ₁, λ₂) вполне естественно говорить (писать) о дифракционных спектрах, которых в принципе нет при освещении дифракционной решётки монохроматическим светом.

В условии задания следовало бы указать, что свет от газоразрядной лампы падает нормально на дифракционную решётку.

Кроме того, следовало бы изменить филологический стиль третьего предложения в условии задания. Режет слух оборот “линия с длиной волны λ^”, его можно было бы заменить на “линия, соответствующая излучению длиной волны λ^” или на более краткий — “линия, соответствующая длине волны λ^”.

Формулировки тестов должны быть научно корректными и литературно безупречными. Тесты формулируют совсем не так, как исследовательские и олимпиадные задачи! В тестах всё должно быть точно, конкретно, однозначно.

С учётом приведённого уточнения условия задания имеем:

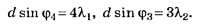
Так как по условию задания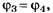то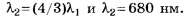

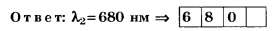
ЦТ 2002 г. Тест № 5 [5]

В5. Найдите наибольший порядок дифракционного максимума для жёлтой линии натрия с длиной волны 5,89·10^-7 м, если период дифракционной решётки равен 5 мкм.

Решение

По сравнению с заданием В5 из теста № 3 ЦТ 2002 г. данное задание сформулировано точнее, тем не менее в условии задания речь следовало бы вести не о “дифракционном максимуме”, а о “главном дифракционном максимуме“.

Наряду с главными дифракционными максимумами всегда имеются ещё и вторичные дифракционные максимумы [6, с. 617, 618]. Не объясняя этого нюанса в школьном курсе физики, тем более надо строго соблюдать сложившуюся научную терминологию и вести речь только о главных дифракционных максимумах.

Кроме того, следовало бы указать, что свет падает нормально на дифракционную решётку.

С учётом вышеприведённых уточнений

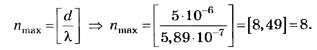
Из неопределённого условия

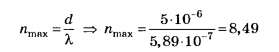
по правилам математического округления числа 8,49 до целочисленного значения опять же получаем 8. Поэтому данное задание, как и предыдущее, следует признать неудачным.

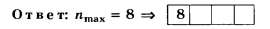
Дополнение 2. Решите вышеприведённое задание, заменив в его условии d=5 мкм на (1=А мкм. Ответ: n_max=6.)

---

Пособие РИКЗ 2003 г. Тест № 6 [7]

В5. Если второй дифракционный максимум находится на расстоянии 5 см от центра экрана, то при увеличении расстояния от дифракционной решётки до экрана на 20% этот дифракционный максимум будет находиться на расстоянии … см.

Решение

Условие задания сформулировано неудовлетворительно: вместо “дифракционный максимум” надо “главный дифракционный максимум”, вместо “от центра экрана” — “от нулевого главного дифракционного максимума”.

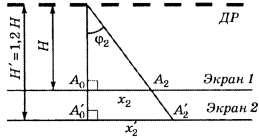
Как видно из приведённого рисунка,

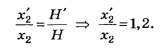
Отсюда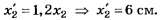

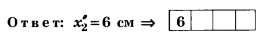
Пособие РИКЗ 2003 г. Тест № 7 [7]

В5. Определите наибольший порядок спектра в дифракционной решётке, имеющей 500 штрихов на 1 мм, при освещении её светом с длиной волны 720 нм.

Решение

Условие задания сформулировано крайне неудачно в научном отношении (см. уточнения заданий № 3 и 5 из ЦТ 2002 г.).

Есть претензии и к филологическому стилю формулировки задания. Вместо словосочетания “в дифракционной решётке” надо было бы использовать словосочетание “от дифракционной решётки”, а вместо “свет с длиной волны” — “светом, длина волны которого”. Длина волны — не нагрузка к волне, а её основная характеристика.

С учётом уточнений

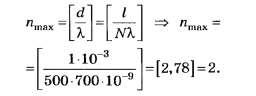
По всем трём вышеприведённым правилам округления чисел округление числа 2,78 до целочисленного значения даёт 3.

Последний факт даже при всех недостатках формулировки условия задания делает его интересным, так как позволяет на тестовом уровне различить правильное (n_max=2) и неправильное (n_max=3) решения.

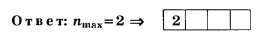
Много заданий на рассматриваемую тему содержится в ЦТ 2005 г. [8].

В условиях всех этих заданий (В1) надо добавить ключевое слово “главный” перед словосочетанием “дифракционный максимум” (см. комментарии к заданию В5 ЦТ 2002 г. Тест № 5).

К сожалению, во всех вариантах тестов В1 ЦТ 2005 г. численные значения d (l,N) и λ подобраны неудачно и всегда дают в дробях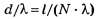

число “десятых” меньше 5, что не позволяет на тестовом уровне отличить операцию выделения целой части дроби (правильное решение) от операции округления дроби до целочисленного значения (ложный след). Это обстоятельство ставит под сомнение целесообразность использования этих заданий для объективной проверки знаний абитуриентов по рассматриваемой теме.

Похоже на то, что составители тестов увлеклись, образно говоря, приготовлением различных “гарниров к блюду”, не думая об улучшении качества основной компоненты “блюда” — подборе численных значений d (l,N) и λ с целью увеличения числа “десятых” в дробях d/λ=l/(N*λ).

ЦТ 2005 г. Вариант 4 [8]

В1. На дифракционную решётку, период которой d₁=1,2 мкм, падает нормально параллельный пучок монохроматического света с длиной волны λ=500 нм. Если её заменить на решётку, период которой d₂=2,2 мкм, то число максимумов увеличится на … .

Решение

Вместо “свет с длиной волны λ” надо “свет длиной волны λ” . Стиль, стиль и ещё раз стиль!

Так как

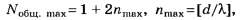
то с учётом того, что X — const, a d₂>di,

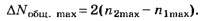
По формуле (4, б)

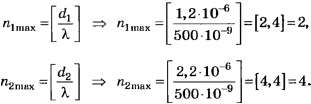
Следовательно, ΔN_{общ. max}=2(4-2)=4

При округлении чисел 2,4 и 4,4 до целочисленных значений тоже получаем соответственно 2 и 4. По этой причине данное задание следует признать простым и даже неудачным.

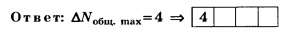
Дополнение 3. Решите вышеприведённую задачу, заменив в её условии λ=500 нм на λ=433 нм (синяя линия в спектре водорода).

Ответ: ΔN_{общ. max}=6

ЦТ 2005 г. Вариант 6

В1. На дифракционную решётку с периодом d= 2 мкм падает нормально параллельный пучок монохроматического света с длиной волны λ=750 нм. Количество максимумов, которые можно наблюдать в пределах угла а=60°, биссектриса которого перпендикулярна плоскости решётки, равно … .

Решение

Словосочетание “света с длиной волны λ” уже обсуждалось выше в ЦТ 2005 г., вариант 4.

Второе предложение в условии данного задания можно было бы упростить и записать так: “Количество наблюдаемых главных максимумов в пределах угла а = 60°” и далее по тексту исходного задания.

Очевидно, что

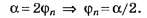
По формуле (4, а)

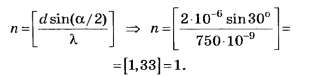
По формуле (5, а)

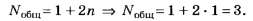
Это задание, как и предыдущее, не позволяет на тестовом уровне объективно определить уровень понимания обсуждаемой темы абитуриентами.

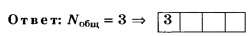
Дополнение 4. Выполните вышеприведённое задание, заменив в его условии λ=750 нм на λ= 589 нм (жёлтая линия в спектре натрия). Ответ: N_o6щ=3.

ЦТ 2005 г. Вариант 7

В1. На дифракционную решётку, имеющую N₁– 400 штрихов на l=1 мм длины, падает параллельный пучок монохроматического света с длиной волны λ=400 нм. Если её заменить решёткой, имеющей N₂=800 штрихов на l=1 мм длины, то количество дифракционных максимумов уменьшится на … .

Решение

Опустим обсуждение неточностей формулировки задания, так как они те же, что и в предыдущих заданиях.

Из формул (4, б), (5, б) следует, что

Следовательно,

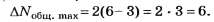
Комментарии о качестве данного задания опустим, “рука… колоть устала”!

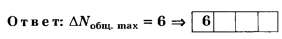
Дополнение 5. Решите вышеприведённую задачу, заменив в её условии λ=400 нм на λ=461 нм (голубая линия в спектре стронция). Ответ: ∆N=6.

ЦТ 2005 г. Вариант 8

В1. На дифракционную решётку с d=1 мкм падает нормально параллельный пучок монохроматического света. Если длина волны света λ=400 нм, то число максимумов, которые образует эта решётка, равно … .

Решение

Злополучное “с” уже перекочевало от “света с длиной волны” к “решётке с d=1 мкм”. Появилось и новое жаргонное выражение — “число максимумов, которые образует эта решётка”. Сама по себе “решётка” не образует дифракционной картины, поэтому следовало бы написать “количество главных максимумов, образованных освещённой решёткой, равно…”.

По формулам (5, б), (4, б)

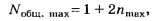
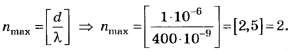
По версии округления чисел [1], [2] целочисленное значение числа 2,5 равно 3, а по версии М. Я. Выгодского [3] — 2.

В сравнении с российским заданием А32 из № 7 Тестов по физике [4], которое рассмотрено выше, данный белорусский тест является ущербным, но на фоне белорусских тестов ЦТ 2005 г. на рассматриваемую в данной статье тему он является лучшим, несмотря на неточности его формулировки.

Итак, N_{общ. max}=1+2*2=5 а по версии округления чисел [1], [2] N_{общ. max}= 1+2*3 =7 (ложный след).

Благодаря этому ложному следу, данное задание в рамках версии округления чисел [1], [2] позволяет на тестовом уровне отличить правильное решение (N_{общ. max}=5) от неправильного (N_{общ. max}=7).

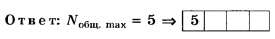
ЦТ 2008 г. Вариант 1 [9]

В12. На дифракционную решётку нормально падает параллельный пучок монохроматического света длиной волны λ=720 нм. Если период решётки d = 5 мкм, то максимальный порядок k_max дифракционного спектра … .

Решение

Задание сформулировано научно некорректно (см. условия предыдущих заданий), но численные значения величин d и λ подобраны удачно и на тестовом уровне правильное решение, определяемое по целой части числа, отличается от неправильного решения, определяемого по округлённому целочисленному значению числа d/λ

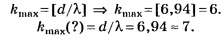
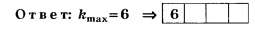
Задания В12 из других вариантов тестов ЦТ 2008 г. предлагаю читателям рассмотреть самостоятельно.

Вывод

За многие годы проведения централизованных тестирований по физике так и не созданы качественные задания на определение порядка главных дифракционных максимумов при перпендикулярном освещении дифракционной решётки монохроматическим светом: то ли условия заданий были сформулированы некорректно, то ли численные значения величин d(l, N) и X были подобраны неудачно и не позволяли на тестовом уровне отличить правильное решение от неправильного.

Список использованной литературы

1. Математика: справочные материалы: кн. для учащихся / В. А. Гусев, А. Г. Мордкович. — Москва : Просвещение, 1988.

2. Математика: учеб. пособие для 4-го класса общеобр. школы с рус. яз. обуч. / Л. А. Лату-тин, В. Д. Чеботаревский; пер. с бел. яз. Т. В. Водневой. — 2-е изд. — Минск : Нар. асвета, 2002.

3. Справочник по элементарной математике. — 27-е изд., испр. / М. Я. Выгодский. — Москва : Наука, 1986.

4. Тесты по физике. 11 кл. / Центр тестирования Министерства образования России. — Москва : Просвещение, 2001.

5. Тесты. Физика. Русский язык: варианты и ответы централизованного тестирования: пособие для подготовки к тестированию / Респ. ин-т контроля знаний. — Минск : Асар, 2003.

6. Справочник по физике для инженеров и студентов вузов. — 6-е изд., испр. / Б. М. Яворский, А. А. Детлаф. — Москва : Наука, 1974.

7. Тесты: Физика. Материалы для подготовки к централизованному тестированию / Респ. ин-т контроля знаний. — Мозырь : Белый Ветер, 2003.

8. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Юнипресс, 2005.

9. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Аверсэв, 2008.

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

• дифракция на щели (прямоугольном отверстии)
• дифракция на решётке (набор равноотстоящих друг от друга щелей)

Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Пусть дана плоскость со щелью, шириной , на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

• для дифракционных максимумов

(1)

• где

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

• для дифракционных минимумов

(2)

• где

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке. 

Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Так же, как и для  щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

(3)

Тогда положения максимумов и минимумов дифракции:

• для главных дифракционных максимумов (рис. 3)

(4)

• где

• для дифракционных минимумов

(5)

• где

Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум — , тогда, исходя из (4):

(6)

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.

Угол

отклонения лучей, соответствующий
максимуму (светлая полоса) при дифракции
на одной щели, определяется из условия

,

где
а
– ширина щели; k
– порядковый номер максимума
(k
= 1,2,3,…).

Угол

отклонения лучей, соответствующий
минимуму (темная полоса) при дифракции
на одной щели, определяется из условия

.

Угол

отклонения лучей, соответствующий
максимуму при дифракции света на
дифракционной решетке, определяется
из условия

,

где
k
= 0,1,2,3,…; d
– период
дифракционной решетки.

Разрешающая
способность
дифракционной решетки равна

где

– наименьшая разность длин волн двух
соседних спектральных линий (

и

),
при которой эти линии могут быть видны
раздельно в спектре, полученном
посредством данной решет­ки; N
– полное
число щелей решетки; k
– порядковый номер дифракционного
максимума.

Формула
Вульфа –
Брэггов
имеет вид

,

где

– угол скольжения, то есть угол между
направлением пучка парал­лельных
рентгеновских лучей, падающих на
кристалл, и гранью кристалла; d
– расстояние между атомными плоскостями
кри­сталла. Формула Вульфа – Брэггов
определяет направление лучей, при
которых возникает дифракционный
максимум.

Задачи

20.1. На щель шириной
а
= 0,05 мм падает нормально монохро­матический
свет (λ= 0,6 мкм). Определить угол φ между
первоначаль­ным направлением пучка
света и направлением на четвертую
тем­ную дифракционную полосу.

20.2
Точечный источник света с длиной волны
λ =0,5мкм расположен на расстоянии а
=
100 см перед диафрагмой с

круглым
отверстием радиуса r
= 1,0
мм. Найти расстояние b
от

диафрагмы
до точки наблюдения, для которой
число зон

Френеля
в отверстии составляет к
= 3.

20.3.
Между
точечным источником света и экраном

поместили
диафрагму с круглым отверстием, радиус
которого

r
можно менять. Расстояние от диафрагмы
до источника и

экрана
равны а
= 100
см и b
= 125
см. Определить длину волны

света,
если максимум освещенности в центре
дифракционной

картины
на экране наблюдается при r₁
= 1,00
мм и следующий

максимум — при r₂
= 1,29 мм.

20.4. На
узкую щель падает нормально монохроматический
свет. Угол φ отклонения пучков света,
соответствующих второй светлой
дифракционной полосе, равен 1⁰.
Скольким длинам волн падающего света
равна ширина щели?

20.5. На щель шириной
а
= 0,1 мм падает нормально монохрома­тический
свет (λ= 0,5 мкм). За щелью помещена
собирающая лин­за, в фокальной плоскости
которой находится экран. Что будет
на­блюдаться на экране, если угол φ
дифракции равен: 1) 17^/;
2) 43^/?

20.6. Сколько штрихов
на каждый миллиметр содержит дифракционная
решетка, если при наблюдении в
монохроматическом свете (λ= 0,6 мкм)
максимум пятого порядка отклонен на
угол φ = 18⁰?

20.7.
На дифракционную решетку, содержащую
n
= 100 штри­хов на 1 мм, падает нормально
монохроматический свет. Зритель­ная
труба спектрометра наведена на максимум
третьего порядка. Чтобы навести трубу
на другой максимум того же порядка, ее
нужно повернуть на угол

= 20°. Определить длину волны света.

20.8.
Дифракционная решетка освещена нормально
падающим монохроматическим светом. В
дифракционной картине максимум второго
порядка отклонен на угол φ₁
= 14⁰.
На какой угол φ₂
откло­нен максимум третьего порядка?

20.9.
Дифракционная решетка содержит n
= 200 штрихов на

1 мм. На решетку падает
нормально монохроматический свет
(λ= 0,6 мкм). Максимум какого наибольшего
порядка дает эта решетка?

20.10. На дифракционную
решетку, содержащую n
= 400 штри­хов на 1 мм, падает нормально
монохроматический свет (λ= 0,6мкм).
Найти общее число дифракционных
максимумов, которые дает эта решетка.
Определить угол φ дифракции, соответствующий
послед­нему максимуму.

20.11. При освещении
дифракционной решетки белым светом
спектры второго и третьего порядков
отчасти перекрывают друг друга. На какую
длину волны в спектре второго порядка
накладывается фиолетовая граница (λ=
0,4 мкм) спектра третьего порядка?

20.12.
На дифракционную решетку, содержащую
n
= 500 штри­хов на 1 мм, падает в направлении
нормали к ее поверхности белый свет.
Спектр проецируется помещенной вблизи
решетки линзой на экран. Определить
ширину b
спектра первого порядка на экране, если
расстояние L
от линзы до экрана равно 3 м. Границы
видимого спектра

= 780 нм,

= 400 нм.

20.13.
Дифракционная картина получена с помощью
дифракционной решетки длиной l
= 1,5 см и периодом d
= 5 мкм. Определить, в спектре какого
наименьшего порядка этой картины
получатся раздельные изображения двух
спектральных линий с разностью длин
волн

= 0,1 нм, если линии лежат в крайней красной
части спектра (

≈ 760 нм).

20.14. Какой наименьшей
разрешающей силой R
должна обла­дать дифракционная
решетка, чтобы с ее помощью можно было
раз­решить две спектральные линии
калия (

= 578 нм и

= 580 нм)? Какое наименьшее число N
штрихов должна иметь эта решетка, чтобы
разрешение было возможно в спектре
второго порядка?

20.15.
С помощью дифракционной решетки с
периодом d
= 20 мкм требуется разрешить дублет натрия
(

= 589,0 нм и

= 589,6 нм) в спектре второго порядка. При
какой наименьшей длине l
решетки это
возможно?

20.16. На грань
кристалла каменной соли падает
параллельный пучок рентгеновского
излучения (λ= 147 пм). Определить расстоя­ние
d
между атомными плоскостями кристалла,
если дифракционный максимум второго
порядка наблюдается, когда излучение
надает под углом θ = 31⁰30^/
к поверхности кристалла.

20.17. Какова длина
волны λ монохроматического рентгеновского
излучения, падающего на кристалл
кальцита, если дифракционный максимум
первого порядка наблюдается, когда угол
θ между на­правлением падающего
излучения и гранью кристалла равен 3⁰?
Расстояние d
между атомными плоскостями кристалла
принять рав­ным 0,3 нм.

20.18.
Параллельный пучок рентгеновского
излучения падает на грань кристалла.
Под углом θ = 65⁰
к плоскости грани наблю­дается максимум
первого порядка. Расстояние d
между атомными плоскостями кристалла
280 пм. Определить длину волны

рентге­новского излучения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Дифракция света:

Среда называется однородной, если ее физические свойства по всему объему одинаковы во всех точках пространства. Среда называется изотропной, если ее физические свойства одинаковы по всем направлениям в пространстве.

Закономерности распространения волн любой природы в различных средах носят универсальный характер.

Рассмотрим процесс распространения волн на поверхности воды.

Волны, возбуждаемые точечным источником S, распространяются на поверхности воды по всем направлениям с одинаковой по модулю скоростью v. Следовательно, фронт волны в этом случае будет иметь вид окружности (рис. 39). Соответственно, если волна будет распространяться в однородной изотропной среде по всем направлениям в пространстве, то ее волновой фронт будет иметь вид сферической поверхности.

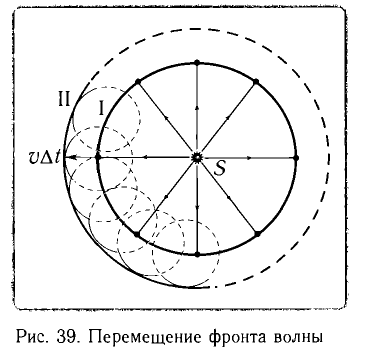
Как видим из рисунка, если в некоторый момент времени t фронт волны занимал положение I, то через промежуток времени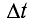

Общие закономерности процесса распространения волн объяснил Гюйгенс, сформулировав в «Трактате о свете» принцип, позволяющий определить положение волнового фронта с течением времени. Согласно принципу Гюйгенса:

Таким образом, согласно принципу Гюйгенса для нахождения положения волнового фронта через промежуток времени 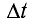проведем окружности радиусом l = v 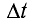(см. рис. 39), представляющие собой фронты вторичных волн, с центрами на фронте в положении I.

Соответственно, огибающая вторичных волн (1, 2, 3 и т. д.) определяет новое положение волнового фронта в момент t + 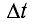— положение II. Напомним, что огибающей называется поверхность, касательная ко всем вторичным волнам.

«Линия, перпендикулярная волновому фронту, называется лучом (волновым лучом). Волновой луч определяет направление распространения волны, а также направление переноса энергии волной.

На очень больших расстояниях от точечного источника волны, излучаемые им, можно считать плоскими. Например, световые лучи в приходящем на Землю солнечном излучении являются практически параллельными друг другу.

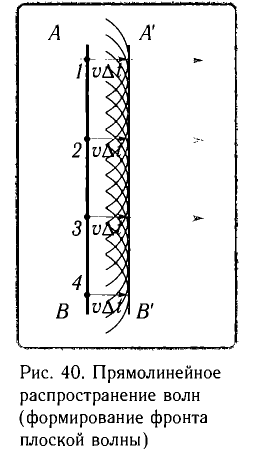
Принцип Гюйгенса объясняет прямолинейное распространение волн в однородной среде. Поскольку в такой среде радиусы фронтов вторичных волн (v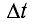) одинаковы на всех участках (рис. 40), то волновой фронт (А’В’) плоской волны с течением времени перемещается в одном и том же направлении, оставаясь параллельным своему начальному положению АВ.

Однако различные волны в однородной среде не всегда распространяются прямолинейно, поскольку наблюдаются отклонения от закона прямолинейного распространения. Действительно, стоя за углом дома, мы хорошо слышим, что едет автомобиль, хотя не видим его, поскольку находимся в области «тени». Таким образом, звуковые волны как бы «заворачивают за угол», в то время как световым волнам этого сделать не удается.

Явление отклонения распространения волн от прямолинейного вблизи краев препятствий и огибания волнами препятствий получило название дифракции (рис. 41).

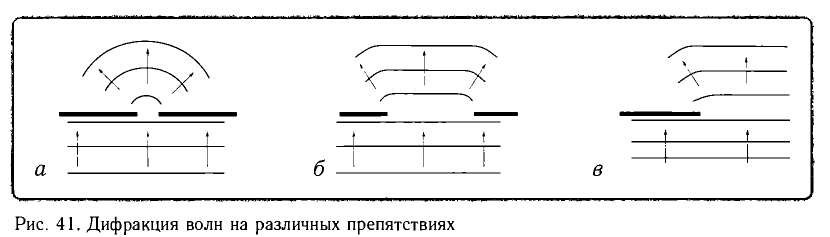
Явление дифракции служит одним из подтверждений волновой природы наблюдаемого процесса.

Для проявления дифракции размеры препятствий (отверстий) должны быть меньше или сравнимы с соответствующей длиной волны, вот почему в рассмотренном примере звук

( )

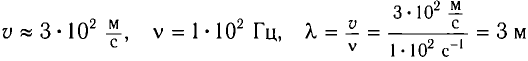смог «завернуть за угол», а свет, отраженный от автомобиля (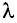= 500 нм = 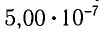), — нет.

Изучая дифракцию света, французский физик Огюстен Жан Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн, которые являются когерентными. Принцип Гюйгенса — Френеля позволил охарактеризовать явление дифракции количественно:

• все вторичные источники, расположенные на волновом фронте, когерентны между собой. Для расчета амплитуды огибающей волны в данной точке пространства следует учесть интерференцию вторичных волн от всех участков волнового фронта в начальном положении.

Таким образом, согласно Френелю дифракция света объясняется интерференцией вторичных волн от различных участков начального положения волнового фронта.

Для наблюдения дифракции света используется дифракционная решетка.

Дифракционной решеткой называют оптический прибор, предназначенный для очень точного измерения длин волн и разложения света в спектр.

Дифракционная решетка состоит из большого числа равноотстоящих параллельных штрихов (щелей), нанесенных на стеклянную или металлическую поверхность. Длина решеток составляет 10—15 см. Они содержат 10 000—20 000 штрихов на 1 см.

Рассмотрим дифракционную решетку, представляющую собой систему из N одинаковых равноотстоящих параллельных щелей (прозрачные участки) в плоском непрозрачном экране (рис. 42). Если ширина каждой щели b, ширина непрозрачной части между щелями а, то величина d = a + b называется постоянной решетки или ее периодом.

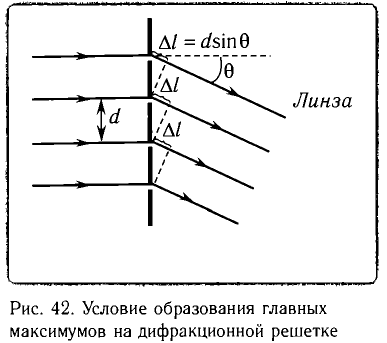
Пусть на решетку, постоянная которой равна d, падает плоская волна, длина которой 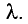Из принципа Гюйгенса следует, что волны, дифрагировавшие на щелях, распространяются за ней по всем направлениям.    

Собирающая линза фокусирует параллельные лучи (вторичные волны) в одну точку на экране, расположенном в фокальной плоскости линзы. Далее вторичные волны, испущенные разными щелями, интерферируют на экране, усиливая или ослабляя друг друга в зависимости от разности хода между ними. Таким образом, на экране получается дифракционная картина в виде системы светлых и темных полос.

Наиболее яркие дифракционные максимумы получили название главных дифракционных максимумов.

Условие образования главных дифракционных максимумов, наблюдаемых под углами 9 с использованием дифракционной решетки, имеет вид:

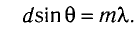
Здесь m = О, ±1, ±2, … — порядок максимума, или порядок спектра, 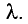— длина волны падающего излучения.

Полученное условие образования главных дифракционных максимумов имеет наглядный физический смысл: на отрезке, равном разности хода от соседних щелей 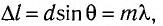укладывается целое число длин волн.

В этом случае вторичные волны от всех щелей решетки приходят в точку наблюдения синфазно (с фазами, отличающимися на число, кратное ) и усиливают друг друга.

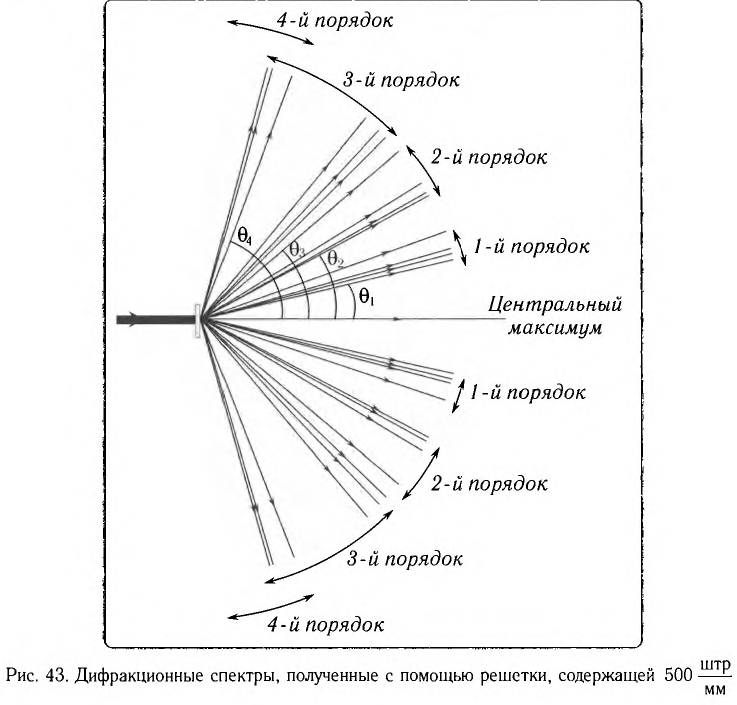
Таким образом, дифракционная картина на экране представляет собой чередующиеся максимумы и минимумы интенсивности излучения. Центральный максимум (m = 0) называется нулевым. Дифракционные максимумы, соответствующие m= 1, образуют спектр первого порядка, m = 2 — спектр второго порядка и т. д. (рис. 43).

Между максимумами интенсивности расположены минимумы, так как при изменении угла 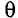на отрезке 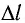(см. рис. 42) уже не будет укладываться целое число длин воли. Следовательно, вторичные волны придут в точку наблюдения в противодействии, ослабляя результирующее действие.

По мере увеличения числа щелей (штрихов) дифракционной решетки максимумы на экране становятся более узкими, а расстояния между ними более широкими (рис. 44). При этом происходит перераспределение энергии падающего излучения, большая часть которой приходится на максимумы.

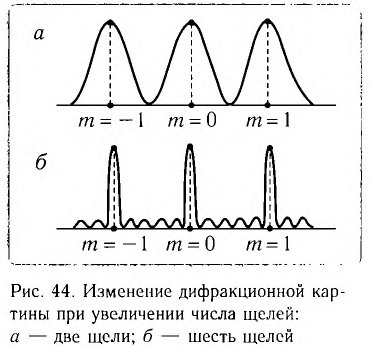
При падении белого света на решетку спектральные максимумы любого порядка (кроме нулевого) содержат все цвета радуги (рис. 45, а).

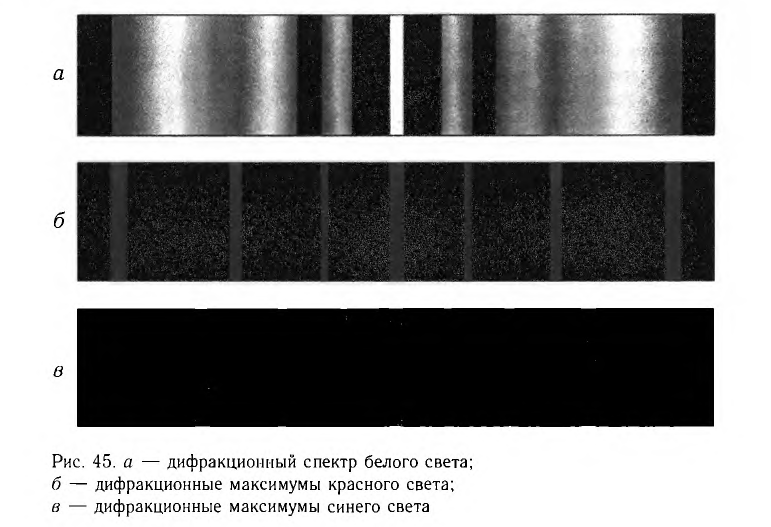
В дифракционном спектре больше всего отклоняются от начального направления распространения красные лучи (рис. 45, б), меньше всего — синие (рис. 45, в), что и следует из формулы для определения дифракционных максимумов решетки.

Первая дифракционная решетка, сконструированная американским ученым Дэвидом Риттенхаузом, состояла из волосков диаметром около 0,1 мм и длиной 10 мм, натянутых параллельно на расстоянии порядка 0,2 мм один от другого. Немецкий физик Йозеф Фраунгофер вместо волосков использовал штрихи, наносимые на стекло алмазным острием. Их число на 1 мм решетки достигало у него 300.

Направления, в которых наблюдаются минимумы интенсивности при дифракции света на двух щелях, остаются минимумами для дифракции на дифракционной решетке. Однако к ним добавляются минимумы, связанные с интерференцией излучения, идущего от каждой из щелей (см. рис. 44). Эти минимумы легко определить из условия, что разность хода света от соседних щелей в данном направлении должна быть кратна нечетному числу полуволн.

Пример №1

Определите угол отклонения 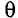излучения зеленого цвета ( 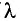= 0,55 мкм) в спектре первого порядка, полученном с использованием дифракционной решетки, период которой d = 0,020 мм.

Решение

Условие дифракционных максимумов определяется соотношением

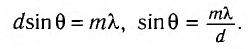
Откуда находим

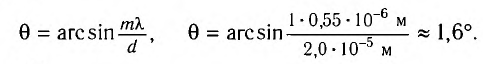
Ответ: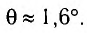

Пример №2

На дифракционную решетку, имеющую N=500 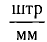 падает монохроматическое излучение с длиной волны 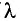= 550 нм. Определите наибольший порядок 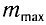дифракционного максимума, который можно наблюдать при нормальном падении излучения на решетку.

Решение

Условие дифракционных максимумов определяется соотношением

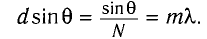
Следовательно,

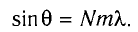
Наибольшее значение 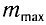 дифракционного максимума наблюдается при угле 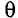, близком к 90°. Вследствие этого будем считать, что

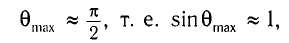
тогда наибольшее значение максимума находится по формуле

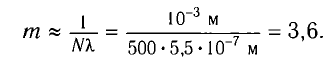
Для определения 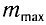 необходимо взять целую часть полученного значения, т. е.

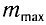= 3.

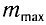Ответ: = 3.

Дифракция света и интерференция

Весной радуемся появлению цветных блесков в воздухе после дождя, на мыльном пузыре, на масле, разлитом на асфальте. Но мы не задумываемся над тем, как они появляются. Причиной этого является интерференция света. Явление интерференции свойственно волнам любой природы. Для осмысления этого явления начнем изучение интерференции механических волн.

При распространении волн в какой-либо среде они ведут себя самостоятельно, как будто нет других волн. Это называется принципом суперпозиции (независимость) распространения волн. Результирующее смещение частицы в пространстве в произвольное время равно геометрической сумме смещения волновых процессов, в которых участвовала частица. Например, если в среде распространяются две волны, то они самостоятельно друг от друга будут действовать на частицу, находящуюся в определенной точке. Если частоты этих волн равны и разница фаз не меняется, то в точке, где они встречаются, они усиливают друг друга или погашают. Это явление называется интерференцией волн. Волны, имеющие равные частоты и у которых разница фаз не меняется, называются когерентными волнами. Явление усиления или погашения друг друга при встрече когерентных волн называется интерференцией волн. В каких случаях они друг друга усиливают или погашают? Для этого рассмотрим встречу волн, выходящих из двух когерентных источников (рис. 4.13).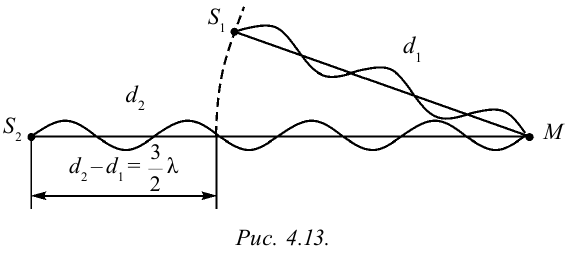 

Путь, пройденный волной, вышедшей из источника 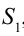, до точки М, равен 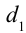. Путь, пройденный волной, вышедшей из источника  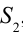 до точки М, равен 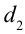. В таком случае 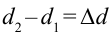– называется разностью хода волны. Если разность хода будет кратной четному числу половины длины волны: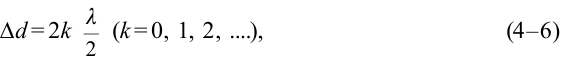

в этой точке наблюдается усиление колебания. Выражение (4-6) называется условием максимума интерференции.

Если разность хода будет кратной нечетному числу длины волны: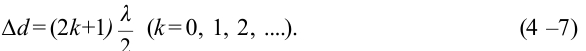

В этой точке наблюдается погашение колебания. Выражение (4-7) называется условием минимума интерференции.

Интерференция света является частным случаем интерференции механических волн. Для наблюдения этого явления две световые волны, испущенные двумя когерентными источниками, должны встречаться в одной точке пространства. Однако сколько бы ни выбрали отдельных источников, световые излучения, испущенные ими, не будут когерентными. Поэтому световое излучение, испущенное одним источником, искусственно делят на два излучения и получают когерентные волны.

Метод Юнга (1801 год)

Этот метод приведен на рис. 4.14. Солнечный луч проникает в темную комнату через маленькую щель S. Этот луч, проходя между двух щелей 5, и разделяется на два луча. При пересечении их на экране, в центральной части создастся белая полоса, в крайних частях – цветные полосы. Юнг в своих экспериментах точно определил длину волны света. Для крайней фиолетовой части спектра длину волны берут 0,42 мкм, для красного света – 0,7 мкм.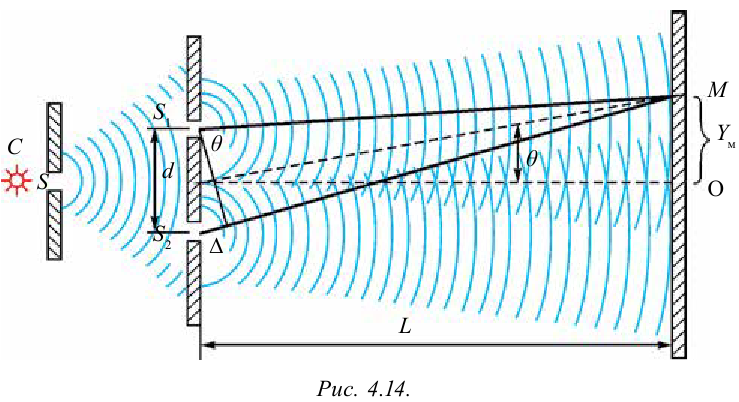

• Заказать решение задач по физике

Цвета на тонких пленках

Вернемся к цветам на масле, разлитом на асфальте, и на мыльных пузырях. Белый свет падает на тонкую пленку (рис. 4.15). Часть падающей волны (волна 1) отражается от верхней поверхности пленки. Часть проходит внутрь пленки и отражается от нижней поверхности (волна 2).

Две отраженные волны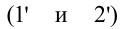 различаются пройденным путем. Когда они встречаются в восприятии глазом, наблюдается картина интерференции. Из-за того что белый цвет состоит из волн с длиной волны от 380 до 760 нм, в различных точках воспринимающего глаза они усиливают друг друга и мы видим цветное изображение.

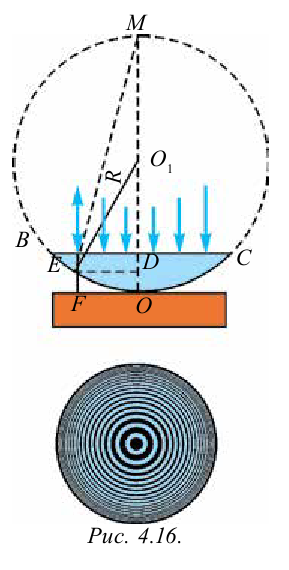
Кольца Ньютона

Пусть на тонкую пластину поставлена линза с выпуклой поверхностью (рис. 4.16). Здесь между плоской параллельной пластиной и поверхностью линзы, касающейся ее в точке О, имеется слой воздуха. Свет, падающий на плоскую поверхность линзы, отражается от верхнего и нижнего слоя воздуха. При встрече этих лучей наблюдается интерференция.

Если устройство будет освещено монохроматическим (только одного цвета) лучом, картина интерференции выглядят в форме светлых и темных колец. Если устройство будет освещено белым светом, то будут видны темные пятна в отраженном свете от точки касания линзы с поверхностью. Вокруг нее располагаются цветные кольца. Путем измерения радиуса кольца соответствующего

порядка можно определить длину волны света или радиус кривизны линзы: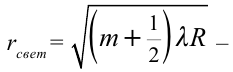
 – радиус светлых колец; R радиус кривизны линзы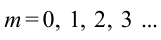 

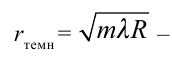 радиус темных колец.

Дифракция света

Люди давно заметили, что свет заходит за края преграды, встречающейся на своем пути. Научное объяснение этого явления первым дал Ф. Грималди. Он объясняет причину того, что тень, которая появляется за предметами, тусклая. Это явление он назвал дифракцией. Таким образом, огибание волнами, встречающими препятствия на своем пути, называется дифракцией волн. При этом не выполняется закон прямолинейного распространения света. Чтобы наблюдалась дифракция, размер преграды должен быть меньше, чем длина падающей на него волны. Дифракцию света также можно увидеть при прохождении света через узкие щели. Здесь размер щели тоже должен быть меньше, чем длина падающей на нее волны.

Для получения четкой и точной дифракционной картины пользуются дифракционной решеткой. Дифракционная решетка состоит из многочисленных преград и щелей, которые пропускают и отражают. Дифракционная решетка по расположению преград делится на два вида: упорядоченные и неупорядоченные дифракционные решетки.

В упорядоченных дифракционных решетках щели расположены в строго определенном порядке. В неупорядоченных дифракционных решетках щели располагаются беспорядочно.

Для изготовления плоской упорядоченной дифракционной решетки берется прозрачная пластина и с помощью лезвия наносятся параллельные и очень близко расположенные друг к другу линии. Нанесенные линии служат как щель, а расстояния между ними как преграда. Пусть ширина щели будет а, ширина преграды в. Тогда 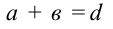называется постоянной, или периодом решетки.

Рассмотрим прохождение света через дифракционную решетку (рис. 4.17).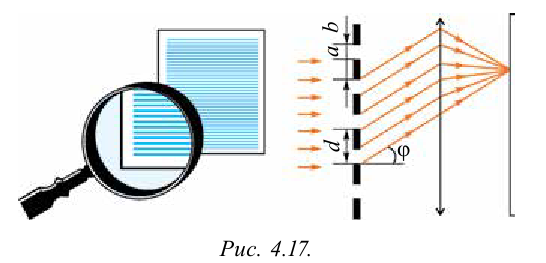

Пусть монохроматическая волна падает перпендикулярно к поверхности решетки. Вторичные волны, прошедшие через щель, в результате явления дифракции отклоняются на угол ср. Затем собираясь, они направляются на экран. На экране появится дифракционная картина,  в виде чередующихся светлых полос, разделенных затемненными промежутками.

При этом постоянная решетки d, длина волны света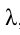, угол отклонения луча на решетке ф связаны с помощью формулы:

здесь: 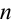-порядковый номер дифракционных максимумов. Если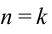

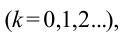при встрече волны усиливают друг друга. Если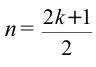, тогда волны друг друга гасят.

Наблюдаемые явления интерференции и дифракции доказывают, что свет имеет волновые свойства. Эти явления используют в технике. Например, прибор, называемый интерферометром, является очень чувствительным. С его помощью можно точно измерить маленькие углы, определить длину волны света, длину маленьких отрезков, показатели преломления света различных веществ, проверить шероховатость поверхности, а также определить степень блеска.

Пример №3

На дифракционную решетку падает монохроматический свет с длиной волны 500 нм. Если спектр второго порядка наблюдается под углом 30°, чему равна постоянная решетки?
Дано: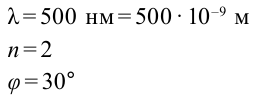  Найти: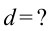

Формула: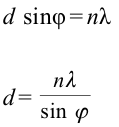

Решение: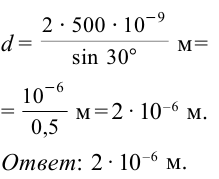

Дисперсия света и спектральный анализ

Вопрос о цвете разных тел и веществ интересовал людей с давних времен. Почему Солнце, заходя за горизонт, краснеет? Почему появляется радуга? Почему при прохождении света через некоторые минералы, они блестят? Ответы на подобные вопросы нашлись только во времена Ньютона. В 1666 году И. Ньютон написал о своем эксперименте следующее: «Я при обработке различных оптических стекол для проверки известных явлений по цвету изготовил треугольную стеклянную призму. В этих целях я затемнил комнату и для поступления солнечного луча на окне сделал маленькую дырку. Я расположил призму так, чтобы луч попадал на призму и, отражаясь от нее, собирался на стене. Таким образом, наблюдение полученных разнообразных и усиленных цветов оставили у меня большое удовольствие».

Полученный набор разных цветов, которые появлялись при прохождении света через призму, Ньютон назвал спектром (от лат. spectrum – увидеть) (рис. 4. 20).

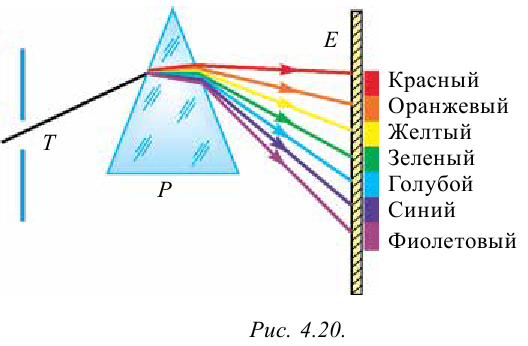
При закрывании щели стеклом красного цвета Ньютон наблюдал на стене только красное пятно, при закрывании щели стеклом зеленого цвета он наблюдал на стене только зеленое пятно. При изучении спектра он установил, что лучи разного цвета преломляются по-разному.

Например, красный цвет преломляется меньше, чем другие, а фиолетовый цвет – больше всех остальных.

Ньютон не знал причину этого. Но этот эксперимент доказал, что белый цвет является сложным цветом. Он состоит из семи цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Имеются и другие эксперименты Ньютона, доказывающие, что белый цвет является сложным цветом. Ньютон взял окружность и, разделив ее на секторы, раскрасил их в семь разных цветов. Эту окружность он закрепил на ось вращения двигателя. При определенной скорости вращения разноцветная окружность выглядит как белая.

Если на пути света, разделенного на разные цвета, после прохождение через первую призму поставить призму под углом 180°, она выполняет функцию собирающей линзы. В точке сбора лучей, выходящих из призмы, получается белый цвет (рис. 4.21).

Открытое Ньютоном явление получило название дисперсия света (от лат. dispеrge – рассеять). Таким образом Ньютон доказал, что белый луч Солнца состоит из суммы лучей разных цветов. То, что разные предметы и вещи имеют разные цвета, объясняется тем, что некоторые цвета поглощаются, а некоторые отражаются. Абсолютно черные тела поглощают все лучи, а белые – отражают.

Согласно волновой теории света, свет – это волны, распространяющиеся в пространстве с большой скоростью. Цвет световой волны зависит от частоты.

Длина волны световых волн очень короткая. Например, красный луч имеет самую большую длину волны, его значение 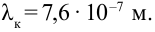Самая маленькая длина волны принадлежит фиолетовому лучу, его значение 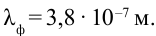Длина волны других лучей лежит между ними.

В 1873 году английский ученый Дж. Максвелл теоретически доказал, что свет состоит из электромагнитных волн, распространяющихся со скоростью 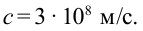Эту теорию экспериментально доказал Г. Герц.

Отсюда можно сделать вывод: лучи, имеющие разные цвета, в среде распространяются с различной скоростью. При переходе света из одной среды в другую меняется его длина волны, но частота не меняется. Нам известно, что скорость волны 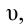длина волны 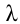и частота v связаны следующим образом: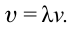

Если учесть связи показателя преломления света 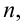скорость распространения света в вакууме 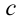и скорость распространения света в среде 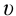(вспомните из 9-го класса):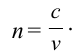 

Получается, что показатель преломления луча в среде для разных лучей будет разным.

Зависимость показателя преломления света от длины волны называется дисперсией.

Это объясняет, почему лучи, прошедшие через призму, отклоняются на разные углы. Таким образом, скорость красного луча в любой среде будет больше, чем фиолетового. Например, в воде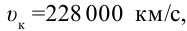 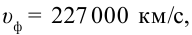в сульфиде углерода 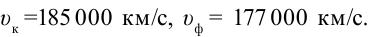В вакууме не наблюдается дисперсии света, так как в вакууме все световые волны распространяются с одинаковой скоростью.

В 1807 году английский физик Томас Юнг, комбинируя красный, зеленый и голубой цвета, доказал, что возможно получить белый цвет. Также, комбинируя красный, зеленый и голубой цвета, можно получить другие цвета (рис. 4.22).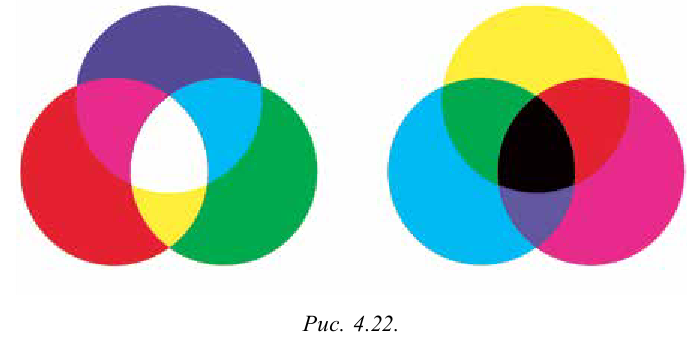

Красный, зеленый и голубой цвета Юнг назвал первичными лучами. Никакой из этих первичных цветов невозможно получить из комбинации других цветов. Это можно легко проверить, освещая экран лучом красного, зеленого и голубого цветов. В том месте, где накладываются эти три цвета, образуется белый цвет.

При смешивании красного и голубого цветов появится темный цвет, при смешивании красного и зеленого цветов появится желтый цвет. В современных телевизорах и на экране компьютера цветное изображение создается благодаря соединению этих трех цветов.

Если через призму пропустить свет из разных источников, никакой из них (кроме лазера) не является монохроматическим, т.е. не излучает волны с одинаковой частотой. Нагретые тела тоже излучают волны разного спектра. Их спектр можно разделить на три вида.

Солнечный спектр или спектр лампы накаливания является непрерывным. Свет, испущенный нагретым веществом в твердом или жидком состоянии и сильно сжатыми газами, имеет непрерывный спектр.

Линейчатый спектр

В таком спектре имеется одна линия. Такой спектр испускает атомы, не связанные друг с другом. Отдельные атомы испускают электромагнитные волны с одной длиной волны.

Полосатый спектр

Отдельные слабо связанные или не связанные молекулы излучают спектр в виде отдельных полос, разделенных темными промежутками. Если поставить красное стекло на пути света, излучаемого лампой, через него проходит только красный свет, а остальные лучи поглощаются. Если белый луч пропустить через неизлучающий газ, то на фоне непрерывного спектра источника появятся черные линии. Причиной этого является поглощение газом лучей некоторых частот. Исследования показали, что нагретое тело испускает свет тех длин волн, которые оно поглащает.

Каждый химический элемент имеет свойственный только ему спектр. Подобно неповторяемости отпечатков пальцев, спектр каждого элемента также не похож на другие.

Определение состава химического вещества по его спектру называется спектральным анализом. Этот метод является очень чувствительным. С его помощью можно обнаружить элемент в составе сложного вещества, если даже его масса не превышает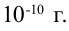

Такой анализ в основном имеет качественный характер, т.е. можно определить, какие элементы имеются в веществе. Однако определить количественное значение этих элементов сложно. Так как при низких температурах вещества большинство спектральных линий не проявляют себя.

В настоящее время определены спектры всех атомов, составлены их таблицы (рис. 4.23). С помощью спектрального анализа были открыты такие химические элементы, как рубидий, цезий и другие. Слово «цезий» означает «небесно-голубой».

Спектр элемента цинка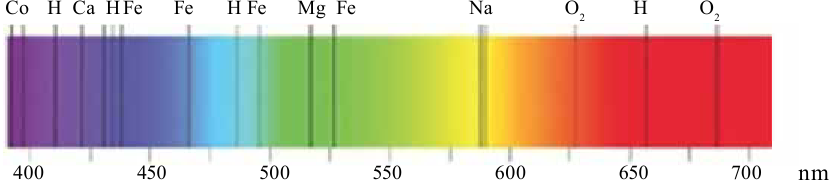

Именно благодаря спектральному анализу стало возможным определить химический состав Солнца и звезд. Другими методами его определить невозможно. Следует сказать, что элемент гелий сначала открыли на Солнце, а затем нашли в атмосфере Земли. «Гелий» означает «солнечный». Спектральный анализ проводится не только с помощью спектра испускания, но и спектра поглощения.

Пример №4

Показатель преломления линзы для красного света равен 1,5, для фиолетового – 1,52. Две поверхности линзы имеют одинаковый радиус кривизны, равный 1 м. Определите разницу между фокусными расстояниями линзы для красного и фиолетового лучей.

Дано: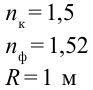  Найти: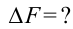

Формула: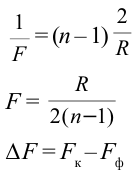

Решение: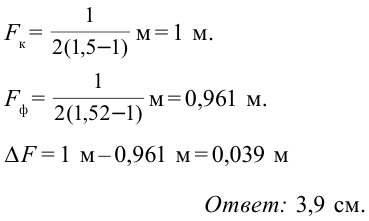

Дифракция волн и дифракция света

Световой луч – линия, вдоль которой распространяется световая энергия.

Световые лучи бывают параллельные, дивергентные (расходящиеся) и конвергентные (сходящиеся). Лучи, падающие на земную поверхность из источников, находящихся на очень больших расстояниях, например, от Солнца, звезд. Луны, принято считать параллельными.

Свет в вакууме и однородной среде распространяется прямолинейно.

Однородной называется среда, в которой её свойства по всему объёму одинаковы.

Образование тени является результатом прямолинейного распространения света.

 Прогуливаясь на природе, вы возможно обращали внимание на паутину, искусно сплетенную пауками. Иногда она привлекает внимание, поблескивая всеми цветами радуги.

Волновая поверхность и фронт волны

Закономерности распространения любых волн в разных средах носят универсальный характер. Например, колебания, созданные в точке падения капли на неподвижной водной поверхности, распространяются с течением времени с одинаковой скоростью, охватывая определенную часть среды (b). С течением времени волна, продолжая распространяться, возмущает еще большую часть водной поверхности. Значит, в процессе распространения волны поверхность воды (среда) состоит из части, в которой волна распространилась, и части, в которой еще не распространилась. Линия, отделяющая эти части волны, называется волновой поверхностью.

Волновая поверхность — геометрическое место точек, до которых в данный момент времени дошла волна.

Определенный набор частиц среды, в которой распространяется волна, колеблется в одинаковой фазе. Поверхность, во всех точках которой колебания происходят в одинаковой фазе, называют поверхностью одинаковой фазы, или фронтом волны.

Фронт волны – геометрическое место точек, колеблющихся в одинаковых фазах.

Фронт волны, являясь геометрической концепцией, создает представление о поверхности, проходящей через точки, колеблющиеся в одинаковых фазах (с). Значение фазы колебаний различных последовательных точек среды при распространении волны в ней может иметь различное значение, поэтому в этой среде может одновременно существовать бесконечное количество фронтов волны.

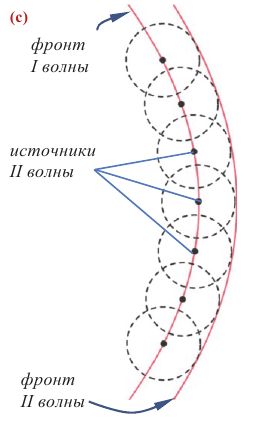
Волна, фронт которой представляет собой плоскость, называется плоской волной, а волну с фронтом сферической или цилиндрической формы называют соответственно сферической или цилиндрической волной.

Плоская волна распространяется в направлении, перпендикулярном плоскому фронту волны.

Дифракция волн и принцип Гюйгенса

Одним из общих свойств, присущих всем видам волн, является их дифракция.

Дифракция волн – явление отклонения волны от геометрического направления распространения при встрече с препятствием (огибание препятствий, проникая за их края).

Огибание волной препятствий связано с соотношением размера препятствия с длиной волны. Явление дифракции наблюдается при соблюдении соотношения:

Здесь 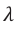– длина волны, D – размер препятствия (или щели) на пути волны, 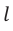– расстояние от препятствия до точки, в которой наблюдается дифракция.

Дифракцию можно объяснить на основе принципа, сформированного Гюйгенсом в 1690 году. Согласно принципу Гюйгенса, каждая точка среды, до которой доходит фронт волны, превращается в источник полусферических волн с частотой колебаний, равной частоте колебаний исходной волны. Касательная к этим сферическим волнам (их называют вторичными волнами) представляет собой новый фронт волны в следующий момент времени (см. с).

Так как направление распространения волны перпендикулярно фронту волны, можно определить луч – это направление распространения волны в любой последующий момент времени.

•    Луч – это нормаль, проведенная к фронту волны в данной точке.

Таким образом, дифракция объясняется с позиций принципа Гюйгенса следующим образом: представим, что на пути волны есть препятствие с щелью, перпендикулярное фронту волны. Вторичные полусферические волны, образованные в точках щели, когда волна доходит до препятствия, проникают за края препятствия – происходит явление дифракции. Но принцип Гюйгенса дал возможность решить проблемы, только связанные с направлением распространения фронта волны, он не смог объяснить изменение амплитуды, а значит, интенсивности распространяющейся по всем направлениям волны. Эта проблема была решена французским физиком Опостеном Френелем (1788-1827) в 1819 году, определившим и объяснившим дифракцию света.

Принцип Гюйгенса-Френеля

Согласно Френелю, развившему принцип Гюйгенса, все точки фронта волны являются источниками когерентных вторичных волн (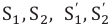и т.д.). Поэтому дифракция света является результатом интерференции – сложения в произвольной точке М когерентных волн, идущих из этих когерентных источников (d).

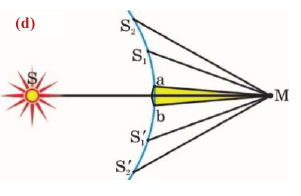
• Дифракция света — явление отклонения от закона прямолинейного распространения света при прохождении вблизи препятствий и попадания в зону геометрической тени. Принцип Гюйгенса, дополненный Френелем принципом интерференции, называется принципом Гюйгенса-Френеля.

Этот (обобщенный) принцип позволил объяснить дифракцию количественно. Длина световой волны очень мала, поэтому дифракция света наблюдается при прохождении света сквозь щели очень малого размера или у края предметов. Поэтому для наблюдения и количественного исследования дифракции света используют специальное устройство, называемое дифракционной решеткой (е).

Дифракционная решетка — оптический прибор, разлагающий свет на спектр и позволяющий измерять длину световой волны.

Дифракционная решетка представляет собой совокупность большого числа непрозрачных штрихов, разделенных очень узкими прозрачными полосками (обычно на 1 мм прибора приходится от 500 до 1200 таких штрихов). Лучи света, падающие на дифракционную решетку перпендикулярно её поверхности, проходя сквозь прозрачные полоски, выходят отклоняющимися на некоторый угол (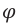). Эти полоски, являясь источниками когерентных волн, распространяют световые волны по всем направлениям. В результате интерференции этих волн на экране образуются дифракционные максимумы и минимумы (см. е).

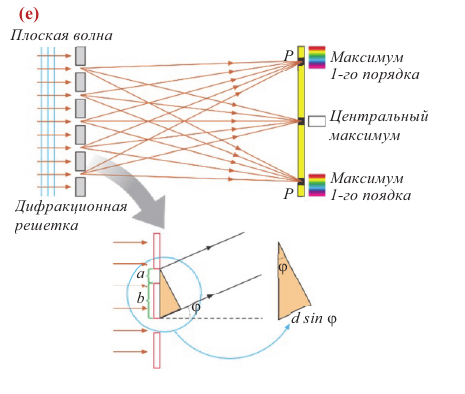
Условие максимума для дифракционной решетки будет иметь вид:

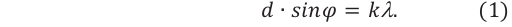
Здесь 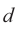– период дифракционной решетки (или постоянная решетки), равная 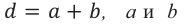– ширина соответственно щели и непрозрачных штрихов, 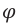– угол отклонения лучей, дающий максимум k-го порядка (k – порядок максимума – порядковый номер максимума от центра картинки). Максимальное значение k соответствует углу отклонения 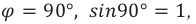получаем:

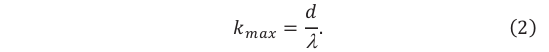
Все максимумы прошедшего через дифракционную решетку белого света (за исключением центрального, нулевого) получаются цветными. Начиная с центра, каждый максимум отражает 7 видимых цветов от фиолетового до красного. Это называют дифракционным спектром. В отличие от дисперсионного спектра полученные в дифракционном спектре более всего отклоняются красные лучи, менее всего отклоняются лучи фиолетового цвета.

Для получения отчётливой дифракционной картины лучше
использовать очень маленькие препятствия (например, тонкую проволоку, круглое
отверстие или круглый экран), либо не располагать экран далеко от препятствий.

Однако чаще всего для получения дифракционной
картины и измерения длины волны пользуются специальным прибором, который
называется дифракционной решёткой.

Она представляет собой совокупность большого
числа параллельных штрихов одинаковой формы, нанесённых на плоскую или вогнутую
полированную поверхность на одинаковом расстоянии друг от друга.

Первая дифракционная решётка, сконструированная
американским учёным Риттенхаузом, состояла из параллельного ряда волосков
диаметром около 0,1 мм и длиной 10 мм, натянутых на расстоянии порядка 0,2 мм
один от другого.

Лишь позже немецкий физик Йозеф Фраунгофер
вместо волосков предложил использовать штрихи, наносимые на стекло алмазным
острием. В его первой решётке число штрихов на 1 мм достигало 300.

В настоящее время принято различать отражательные
дифракционные решётки и прозрачные.

В прозрачных дифракционных решётках штрихи
нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном
экране). Наблюдение ведётся в проходящем свете.

В отражательных решётках штрихи нанесены на
зеркальную (металлическую) поверхность, и наблюдение дифракции ведётся в отражённом
свете.

Если ширина прозрачных щелей (или отражающих
свет полос) равна а и ширина непрозрачных промежутков (или рассеивающих
свет полос) равна b,
то величина, равная d = а + b называется периодом (или
постоянной) решётки. Он показывает, сколько штрихов приходится на один
миллиметр длины решётки:

Рассмотрим элементарную теорию дифракционной
решётки.  Пусть на решётку, постоянная которой равна d, падает плоская монохроматическая волна,
длина которой λ. Из принципа
Гюйгенса следует, что волны, дифрагировавшие на щелях, распространяются за решёткой
по всем направлениям.

Для наблюдения дифракционной картины на экране
между ним и решёткой размещают собирающую линзу таким образом, чтобы экран
находился в фокальной плоскости линзы. Собирающая линза фокусирует на экране
падающие на неё параллельные лучи (вторичные волны).

Допустим, что свет дифрагирует на щелях под
углом φ. Так как щели находятся друг от друга на одинаковых
расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного
направления будут одинаковыми в пределах всей дифракционной решётки:

В зависимости от разности хода между вторичными
волнами, испущенными разными щелями, они интерферируют друг с другом, усиливая
или ослабляя друг друга. В тех направлениях, для которых разность хода равна чётному
числу полуволн, наблюдается интерференционный максимум. В тех же направлениях, где
разность хода равна нечётному числу полуволн, наблюдается интерференционный
минимум. В итоге на экране мы наблюдаем дифракционную картину светлых и тёмных
полос.

Таким образом, в направлениях, для которых углы
удовлетворяют условию

наблюдаются главные максимумы дифракционной
картины.

Эту формулу часто называют формулой
дифракционной решётки. В ней k называется порядком главного максимума и может принимать значения
ноль, один, два и так далее.

Из условия возникновения главных дифракционных
максимумов следует, что при k = 0 для любых длин волн угол φ = 0. Следовательно, прямо по
центру решётки образуется нулевой максимум, который называется также центральным
максимумом. Остальные дифракционные максимумы образуют спектры первого,
второго и так далее порядков.

Естественно, что количество максимумов в
дифракционной картине ограничено, поскольку синус не может принимать значения,
больше единицы.

При падении на решётку белого света центральный
максимум представляет собой изображение источника, так как в этом направлении
собирается излучение всех длин волн. Все остальные максимумы оказываются
окрашенными. Это объясняется тем, что, различным длинам волн соответствуют
различные углы, на которых наблюдаются интерференционные максимумы:

Радужная полоска, содержащая в общем случае
семь цветов — от фиолетового до красного (считается от центрального максимума),
называется дифракционным спектром.

Ширина спектра зависит от постоянной решётки и
увеличивается при её уменьшении. А максимальный порядок спектра определяется из
условия, что «синус угла Фи» меньше либо равен единице:

Мы можем наблюдать дифракционную картину
достаточно просто. Так, если прищуриться, смотря на яркий источник света, то
можно обнаружить радужные цвета. Наши ресницы вместе с промежутками между ними представляют
собой грубую дифракционную решётку. А лазерный диск с бороздками, проходящими
близко друг от друга, подобен отражательной дифракционной решётке.

Для закрепления нового материала давайте с вами
определим постоянную дифракционной решётки, если красная линия (λ = 7
∙ 10^–7 м) в спектре второго порядка получается на расстоянии 25
см от центральной светлой полосы на экране. Расстояние от экрана до
дифракционной решётки равно сорока трём целым трём десятым сантиметра (43,3
см).

Для удобства решения задачи будем считать, что
дифракция наблюдается при нормальном падении на решётку параллельных лучей
белого света.