Как найти диметр шара

Как найти диметр шара

Шар, рассматриваемый в трёхмерном пространстве, представляет собой объёмную геометрическую фигуру.
Любое правильное шаровидное тело состоит из совокупности точек эвклидова (3-хмерного) пространства,
которые находятся на расстоянии от одной из них не далее заданного. Точка, относительно которой
ведётся отсчёт и вокруг которой сосредоточены важные для этого пространственного тела отношения,
получила название центра шара.

Его поверхность, являющаяся своего рода оболочкой, ограничивающей
объём пространственного тела и представляющая совокупность равноудалённых от центра точек, названа
сферой. Расстояние между центром и любой точкой сферы – это радиус шара. Образуется шар, в геометрии
входящий в группу тел вращения, полным оборотом половины плоского круга вокруг своего диаметра,
одновременно выступающего и диаметром шара. Этот отрезок, называемый осью вращения, соединяет
противолежащие точки на поверхности фигуры, называемые полюсами. Одновременно диаметр проходит через
центральную точку шара.

  • Диаметр шара через плошадь поверхности шара
  • Диаметр шара через обьём шара

Способ вычисления диаметра шара при известном значении объёма фигуры

Диаметр шара, представляющий собой удвоенный радиус фигуры, может быть выведен из стандартной
формулы, связывающей его с площадью поверхности: S = 4πR² или S = πD². Отсюда выводим диаметр:

D = √(S ⁄ π)

где S — площадь поверхности шара

Цифр после
запятой:

Результат в:

Пример. Значение площади поверхности (сферы) конкретного шара S = 314.Тогда,
принимая в качестве константы с точностью до сотых π = 3,14, вычисляем диаметр: D = √(314 ⁄ 3,14) = √100 = 10.

Способ нахождения диаметра шара при заданном значении его объёма

Объём шара связан с радиусом фигуры формулой V = 4 ⁄ 3 * πR³. Радиус представляет собой половину
диаметра шара, то есть R = D ⁄ 2. Подставляя в формулу выраженный через диаметр радиус и выполняя
преобразование для выделения диаметра, получаем следующее выражение: V = 4 ⁄ 3 * π(D ⁄ 2)³, V = 4 ⁄
3* πD³ ⁄ 8, отсюда

D = ³√(6V / π)

где V — объём шара

Цифр после
запятой:

Результат в:

Пример. Для примера примем значение объёма шара равным 11,304. Здесь, беря константу
π с точностью до сотых (π = 3,14), получаем: D = ³√(6 * 11,304 / 3,14)
или, выполняя вычисление D=6.

В природе этот пространственный объект имеет множество реальных аналогов, поэтому его свойства и
параметры важны при решении массы научных задач в биологии, астрономии, физике. Ряд распространённых
инженерных, строительных задач также проводится с использованием геометрических вычислений,
связанных с шарообразными конструкциями. Нахождение диаметра шара – одна из них, и она может быть
выполнена несколькими различными способами. Описание двух вариантов вычислений здесь и
представлено.

Источник

Чтобы найти диаметр шара при помощи этого калькулятора, достаточно заполнить любую одну ячейку, введя известное значение, и нажать на кнопку расчета. Программа автоматически вычислит все остальные значения, которые отобразятся в ответе вместе с удобными и понятными формулами.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Радиус (r)

Диаметр (d)

Площадь (S)

Объем (V)

Округление:

Знаков после запятой

* – обязательно заполнить

Источник

У этого термина существуют и другие значения, см. Шар (значения).

Поверхность шара — сфера
r — радиус шара

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Связанные определения[править | править код]

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR².

Основные геометрические формулы[править | править код]

Площадь поверхности S и объём V шара радиуса r (и диаметром d = 2r) определяются формулами:

  • S= 4pi r^{2}
  • S= pi d^{2}
  • V={frac {4}{3}}pi r^{3}

Доказательство

Возьмём четверть круга радиуса R с центром в точке left(0;0right). Уравнение окружности этого круга : x^{2}+y^{2}=R^{2}, откуда y^{2}=R^{2}-x^{2}.

Функция y={sqrt {R^{2}-x^{2}}},xin (0;R) непрерывная, убывающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

{1 over 2}V=pi int limits _{0}^{R}(R^{2}-x^{2})dx=pi cdot {Bigl .}left(R^{2}x-{frac {x^{3}}{3}}right){Bigr |}_{0}^{R}=pi cdot (R^{3}-{frac {R^{3}}{3}})={frac {2}{3}}pi R^{3}

Откуда V={frac {4}{3}}pi R^{3} Ч. т. д.

  • V={frac {pi d^{3}}{6}}

Доказательство

d=2r, V={4 over 3} pi r^3 = {4 over 3} pi left ( {d over 2} right )^3 = {4 over 3} pi frac {d^3} {8} = frac {pi d^3} {6} Ч. т. д.

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

Определения[править | править код]

Пусть дано метрическое пространство (X,rho). Тогда

B_{r}(x_{0})={xin Xmid rho (x,x_{0})<r}.
D_{r}(x_{0})={xin Xmid rho (x,x_{0})leqslant r}.

Замечания[править | править код]

Шар радиуса r с центром x_{0} также называют r-окрестностью точки x_{0}.

Свойства[править | править код]

B_{1}(x)={x},;overline {B_{1}(x)}={x},;D_{1}(x)=X.

Объём[править | править код]

Объём n-мерного шара радиуса R в n-мерном евклидовом пространстве:[1]

{displaystyle V_{n}(R)={frac {pi ^{n/2}}{Gamma ({frac {n}{2}}+1)}}R^{n},}

где Γ — это эйлеровская гамма-функция (которая является расширением факториала на поле действительных и комплексных чисел). Используя частные представления гамма-функции для целых и полуцелых значений, можно получить формулы объёма n-мерного шара, которые не требуют гамма-функции:

{displaystyle V_{2k}(R)={frac {pi ^{k}}{k!}}R^{2k}},
{displaystyle V_{2k+1}(R)={frac {2^{k+1}pi ^{k}}{(2k+1)!!}}R^{2k+1}={frac {2(k!)(4pi )^{k}}{(2k+1)!}}R^{2k+1}}.

Знаком !! здесь обозначен двойной факториал.

Эти формулы также можно свести в одну общую:

{displaystyle V_{n}(R)={frac {2^{left[{frac {n+1}{2}}right]}pi ^{left[{frac {n}{2}}right]}}{n!!}}R^{n}}.

Обратная функция для выражения зависимости радиуса от объёма:

{displaystyle R_{n}(V)={frac {Gamma (n/2+1)^{1/n}}{sqrt {pi }}}V^{1/n}}.

Эта формула также может быть разделена на две: для пространств с чётным и нечётным количеством размерностей, используя факториал и двойной факториал вместо гамма-функции:

{displaystyle R_{2k}(V)={frac {(k!V)^{1/2k}}{sqrt {pi }}}},
{displaystyle R_{2k+1}(V)=left({frac {(2k+1)!!V}{2^{k+1}pi ^{k}}}right)^{1/(2k+1)}}.

Рекурсия[править | править код]

Формулу объёма также можно выразить в виде рекурсивной функции. Эти формулы могут быть доказаны непосредственно или выведены из основной формулы, представленной выше. Проще всего выразить объём n-мерного шара через объём шара размерности n-2 (при условии, что они имеют одинаковый радиус):

{displaystyle V_{n}(R)={frac {2pi R^{2}}{n}}V_{n-2}(R)}.

Также существует формула объёма n-мерного шара в зависимости от объёма (n−1)-мерного шара того же радиуса:

{displaystyle V_{n}(R)=R{sqrt {pi }}{frac {Gamma ({frac {n+1}{2}})}{Gamma ({frac {n}{2}}+1)}}V_{n-1}(R)}.

То же без гамма-функции:

{displaystyle {begin{aligned}V_{2k}(R)&=Rpi {frac {(2k-1)!!}{2^{k}k!}}V_{2k-1}(R)=Rpi {frac {(2k-1)(2k-3)cdots 5cdot 3cdot 1}{(2k)(2k-2)cdots 6cdot 4cdot 2}}V_{2k-1}(R),\V_{2k+1}(R)&=2R{frac {2^{k}k!}{(2k+1)!!}}V_{2k}(R)=2R{frac {(2k)(2k-2)cdots 6cdot 4cdot 2}{(2k+1)(2k-1)cdots 5cdot 3cdot 1}}V_{2k}(R).end{aligned}}}

Пространства младших размерностей[править | править код]

Формулы объёма для некоторых пространств младших размерностей:

Кол-во измерений Объём шара радиуса R Радиус шара объёма V
1 {displaystyle 2R} {displaystyle V/2}
2 pi R^{2} {displaystyle {frac {V^{1/2}}{sqrt {pi }}}}
3 {displaystyle {frac {4pi }{3}}R^{3}} {displaystyle left({frac {3V}{4pi }}right)^{1/3}}
4 {displaystyle {frac {pi ^{2}}{2}}R^{4}} {displaystyle {frac {(2V)^{1/4}}{sqrt {pi }}}}
5 {displaystyle {frac {8pi ^{2}}{15}}R^{5}} {displaystyle left({frac {15V}{8pi ^{2}}}right)^{1/5}}
6 {displaystyle {frac {pi ^{3}}{6}}R^{6}} {displaystyle {frac {(6V)^{1/6}}{sqrt {pi }}}}
7 {displaystyle {frac {16pi ^{3}}{105}}R^{7}} {displaystyle left({frac {105V}{16pi ^{3}}}right)^{1/7}}
8 {displaystyle {frac {pi ^{4}}{24}}R^{8}} {displaystyle {frac {(24V)^{1/8}}{sqrt {pi }}}}
9 {displaystyle {frac {32pi ^{4}}{945}}R^{9}} {displaystyle left({frac {945V}{32pi ^{4}}}right)^{1/9}}
10 {displaystyle {frac {pi ^{5}}{120}}R^{10}} {displaystyle {frac {(120V)^{1/10}}{sqrt {pi }}}}

Пространства старших размерностей[править | править код]

Объём гипершара размерности n единичного радиуса в зависимости от n.

При стремлении количества размерностей к бесконечности объём шара единичного радиуса стремится к нулю. Это может быть выведено из рекурсивного представления формулы объёма.

Примеры[править | править код]

  • Пусть mathbb{R}^d — евклидово пространство с обычным евклидовым расстоянием. Тогда
  • если d=1 (пространство — прямая), то
{displaystyle B_{r}(x_{0})={xin mathbb {R} mid |x-x_{0}|<r}=left(x_{0}-{r},x_{0}+{r}right),}
{displaystyle D_{r}(x_{0})={xin mathbb {R} mid |x-x_{0}|leq r}=left[x_{0}-{r},x_{0}+{r}right].}
 — открытый и замкнутый отрезок соответственно.
 — открытый и замкнутый диск соответственно.
 — открытый и замкнутый стереометрический шар соответственно.
Тогда

См. также[править | править код]

  • Шаровой слой
  • Гиперсфера
  • Сферический слой

Примечания[править | править код]

  1. ↑ Equation 5.19.4, NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.6 of 2013-05-06.

Литература[править | править код]

  • Шар, геометрическое тело // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки на онлайн калькуляторы[править | править код]

  • Вычисление объема и площади шара. Дата обращения: 12 марта 2012. Архивировано из оригинала 8 августа 2011 года.
  • Онлайн-калькуляторы. Дата обращения: 2 июля 2019. Архивировано из оригинала 9 января 2019 года.
  • Математические этюды. Дата обращения: 20 октября 2011. Архивировано из оригинала 18 октября 2011 года. Мультфильм про объём шара
Источник

С помощью этого простого калькулятора можно без труда найти диаметр шара и остальные величины, такие как радиус, площадь и объем шара. Все, что нужно сделать, это заполнить любой один слот и нажать на кнопку “Рассчитать”. В итоге отобразятся все 4 величины вместе с формулами вычисления.

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Радиус (r)

Диаметр (d)

Площадь (S)

Объем (V)

Округление:

Знаков после запятой

* – обязательно заполнить

5
2
голоса

Рейтинг статьи

Источник

Как узнать диаметр

Диаметр – это линия, которая соединяет две точки криволинейной фигуры и при этом проходит через ее центр. В прикладных задачах часто требуется найти диаметр окружности или шара. Диаметр окружности можно найти по ее радиусу, длине и площади круга. Диаметр шара находят по радиусу, объему и площади поверхности.

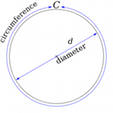
Как узнать диаметр

Инструкция

Диаметр окружности или шара, если известны их радиусы, можно найти, зная, что диаметр в два раз превышает радиус. Таким образом, для нахождения диаметра по радиусу, надо величину радиуса умножить на два:
D = 2*R, где R – радиус фигуры.

Диаметр окружности, если известна ее длина, можно найти по формуле:
D = L/пи, где L – длина окружности, пи – постоянная, приблизительно равная 3,14.

Диаметр круга, если известна его площадь, можно найти по формуле:
D = 2*(S/пи)^1/2, где S – площадь круга.

Диаметр шара, если известен его объем, можно найти используя формулу:
D = (6V/пи)^1/3, где V – объем шара.

Если известна площадь поверхности шара, то его диаметр можно определить по формуле:
D = (S/пи)^1/2, где S – площадь поверхности шара.

Обратите внимание

^ – знак, обозначающий возведение в степень;
^1/2 – по сути извлечение квадратного корня;
^1/3 – извлечение кубического корня.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Добавить комментарий