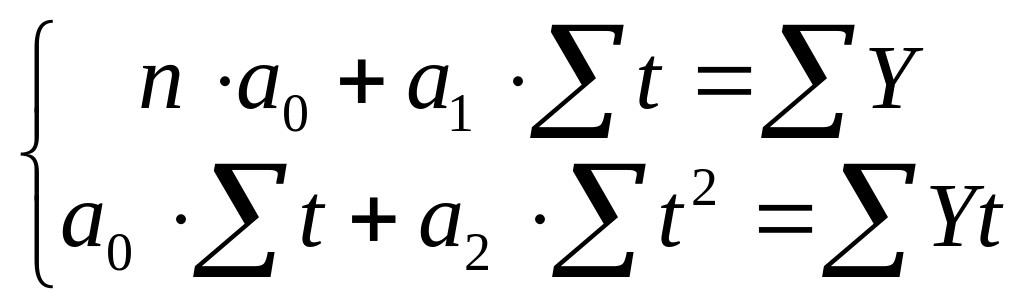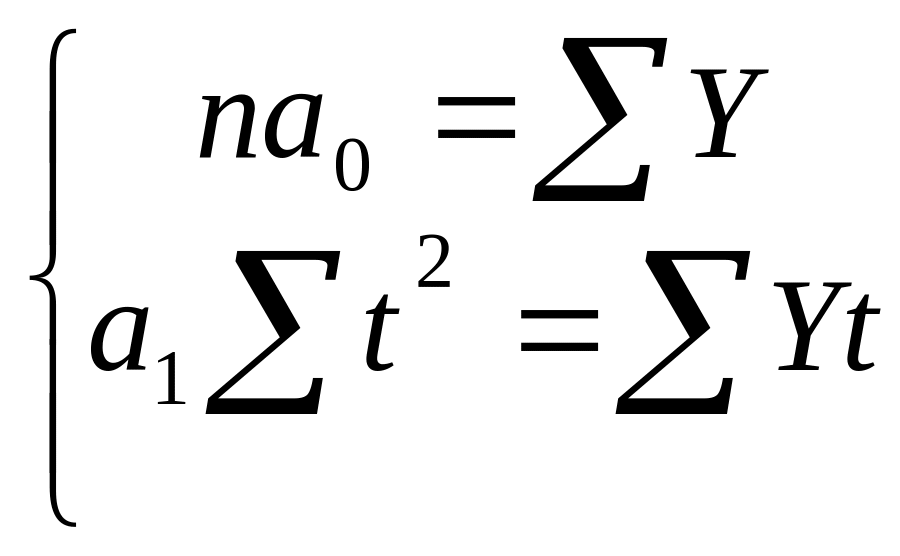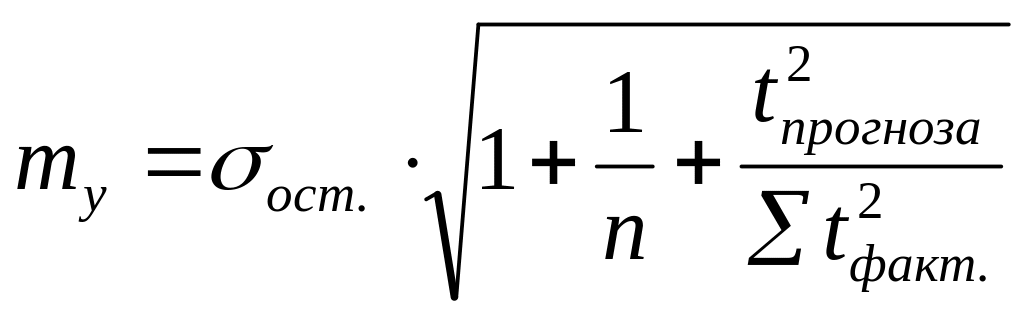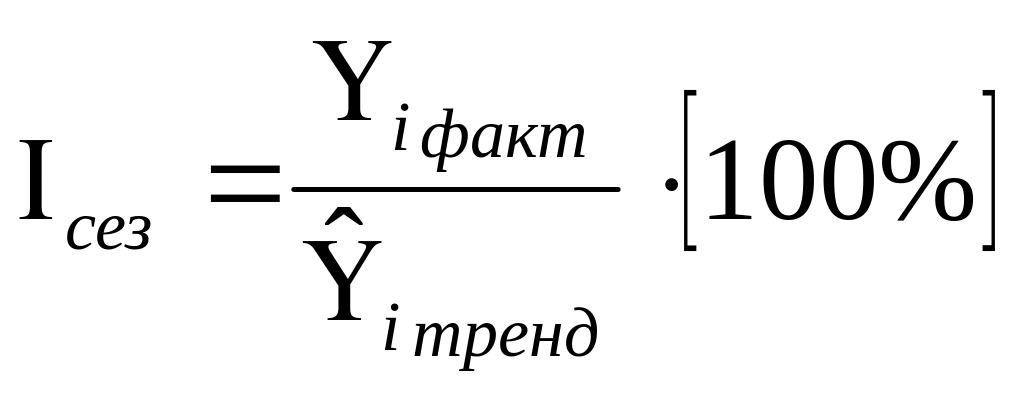Как найти динамику изменения показателя в процентах

Для чего используется понятие процентное изменение – percentage change? Это взаимосвязь между начальным и конечным значением, соответственно, старым и новым. Разница выражается в процентном соотношении.

Данные вычисляются по формуле: ((V2-V1)/V1) × 100. Где V1 – старое значение, а V2 – новое. Приведем пример, xt – переменная. Изменение необходимо определять как Δx=xt–xt-1. В соответствии с формулой, изменение в процентном соотношении будет рассчитываться следующим образом: l00Δxt/xt-1. Возьмем xt=50, xt-1=40. Процентное изменение (percentage change) будет составлять 100(10)/40=25%.

Все расчеты проще всего производить посредством онлайн-калькулятора. Нет необходимости тратить время, вычисляя данные по формуле. Можно просто вставить значения в соответствующие поля и получить результат.

Справка

Зачастую, в конце месяца перед маркетологом или сотрудником отдела продаж стоит задача подготовить отчет с показателями для руководства компании. В отчете требуется посчитать эффективность работы отдела за текущий и прошлый месяц — сравнить разницу за период по лидам или клиентам, продажам, выручки, заключенным договорам, привлеченным партнерам и т.д.

Зная формулу и применяя онлайн инструменты, рассчитать прирост будет не сложно.

Давайте разберемся на простом случае. Например, в феврале вы получили через интернет-магазин 602 заказа. В марте вы запустили контекстную рекламную кампанию и сделали E-mail рассылку по базе подписчиков. Количество заказов немного подросло и составило 964.

Получается, чтобы рассчитать разницу, вам нужно — (964 * 100% / 602) — 100 = 60,13%.

Инструкция

Инструмент определяет процентное или количественное изменение значения.

1. Установите формат в котором будет производиться расчет — в процентах или штуках;
2. В левое окошко укажите абсолютное значение;
3. Во втором окне добавляем фактическое значение.

Программа моментально сравнит и выведет ответ.

Подписаться →

Формулы для расчета показателей ряда динамики.

Подстрочные
символы “ц” и “б” отражают цепной и
базисный способы расчета показателей
ряда динамики.

Абсолютный
прирост
показывает, на сколько больше или меньше
значение уровня ряда с тем значением,
с которым проводится сравнение (соседним
или выбранным за базу сравнения).

или

(7.1)

Коэффициент
роста (темп роста) показывает,
во сколько раз больше или меньше значение
уровня ряда с тем значением, с которым
проводится сравнение (соседним или
выбранным за базу сравнения). Коэффициент
роста может быть выражен в процентах.

или

(7.2)

Темп
прироста характеризует
относительную скорость изменения уровня
ряда в единицу времени. Темп прироста
показывает, на какую долю (или процент)
уровень ряда рассматриваемого периода
больше или меньше базового (выбранного
для сравнения).

или
Т_ц,б=К_ц,б–1
или Т_ц,б=К_ц,б%–100%;
(7.3)

Предыдущий
показатель не отражает «вес» каждого
процента прироста. Например, в двух
бригадах урожайность зерновых выросла
по сравнению с предыдущим годом на 1,2%.
Но это не значит, что в натуральном
выражении это будет составлять одинаковое
количество центнеров. Оценить каждый
процент изменения позволяет следующий
показатель.

Абсолютное
значение 1% прироста
показывает натуральную величину
показателя, приходящегося на 1% изменения
относительно базисного (взятого за
основу сравнения) значения.

(7.4)

Формулы для расчета средних значений показателей ряда динамики:

1)
Средний уровень ряда может быть вычислен
по одной из формул (7.5 – для интервальных
радов; 7.6 – для моментных рядов)

или

(7.5)

(7.6)

2)
Средний абсолютный прирост:

или

(7.7)

где
(n
–1) – число периодов.

1. Средний
   темп роста:

,
(7.8)

где
n
– количество цепных темпов роста уровня
ряда

,
(7.9)

где
n
– число уровней ряда

4)
Средний темп прироста:

или

(7.10)

Средний
уровень ряда рассчитаем по формуле
средней арифметической простой У=1145,057

Средний
темп роста вычислим по любой из формул
8.8 или 8.9 и получим один и тот же результат
К= 0,9913= 99,13%. Это значение отражает среднее
ежегодное снижение численности населения
по сравнению с предыдущим периодом.

Средний темп
прироста (снижения) Т=-0,0087=–0,87%, т.е.
ежегодно на 0,87% уменьшалась численность
населения РБ.

Абсолютное среднее
ежегодное уменьшение численности
населения будут равно Δ =–9,97 тыс. чел.

Все
эти значения показывают ухудшающуюся
демографическую ситуацию в РБ.

Например:

Таблица
7.5. Численность сельского населения РБ
на начало года, тыс. чел.

Годы	Y	Δ	К	Т	А
ц	б	ц	б	ц	б	ц
1	1173,9	–	–	–	–	–	–	–
2	1166,2	-7,7	-7,7	0,993441	0,993441	-0,006559	-0,006559	1173,9
3	1156,5	-9,7	-17,4	0,991682	0,985178	-0,008318	-0,014822	1166,2
4	1146,1	-10,4	-27,8	0,991007	0,976318	-0,008993	-0,023682	1156,5
5	1135,1	-1,1	2309	0,990402	0,966948	-0,009598	-0,033052	1146,1
6	1123,5	-11,6	-50,4	0,989781	0,957066	-0,010219	-0,042934	1135,1
7	1114,1	-9,4	-59,8	0,991633	0,949059	-0,008367	-0,050941	1123,5

В
3. Приемы
выравнивания рядов динамики.

Часто
в рядах динамики сложно определить
общую тенденцию развития. Второй задачей
рядов динамики является выявление таких
периодов развития, которые достаточно
однородны по своим условиям и
взаимодействиям связей между показателями.

Под
тенденцией
понимается общее направление к росту,
снижению или стабилизации уровня явления
с течением времени.

Тенденция
по периодам может не совпадать с общей
тенденцией. Иногда вообще сложно
определить общую тенденцию. В этом
случае прибегают к различным методам
выравнивания ряда для определения его
тенденции:

1) способу укрупнения
интервалов;

2) сглаживанию ряда
с помощью скользящей средней;

3)
производят аналитическое выравнивание
и получают уравнение тренда.

Первый
способ
заключается в переходе от меньших
временных интервалов к большим и расчете
усредненных уровней ряда за укрупненный
интервал. Временной промежуток для
укрупнения интервала производят с
учетом общей длины анализируемого ряда
и величины исходных интервалов. Так,
например, если исходный ряд содержит
информацию за каждый месяц, то можно
перейти к укрупненному интервалу
величиной в квартал. Если представлена
информация по годам, то «укрупнение»
можно произвести за 2,3,4,5 лет в зависимости
от длины исходного ряда.

График
этого ряда изображен на рисунке 7.2, где
видно, что имеются периоды спада
производства продукции и периоды
подъема. Если рассмотреть только часть
графика, начиная с 1998 года по 2005, то
сложно установить общую тенденцию
производства продукции данного вида.
Поэтому более четко общая тенденция
будет просматриваться, если произвести
выравнивание ряда одним из методов.
Так, использование метода укрупнения
интервалов дает результаты, представленные
в таблице 7.6 и 7.7.

Например:

Таблица
7.6. Производство цельномолочной продукции
в пересчете на молоко, тыс. тонн.

Годы	Цельномолочная продукция в пересчете на молоко	Годы	Цельномолочная продукция в пересчете на молоко
1995	801	2001	963
1996	744	2002	906
1997	813	2003	927
1998	952	2004	992
1999	1032	2005	1122
2000	954	2006	1284

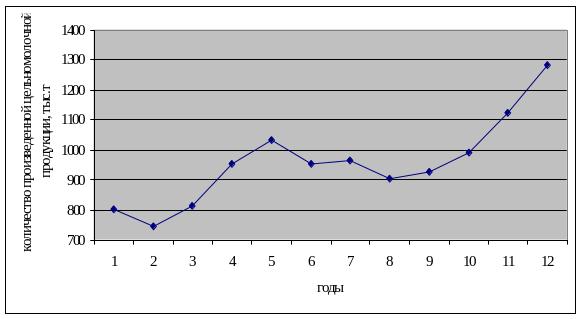
Рисунок
7.2. График динамики производства
цельномолочной продукции в РБ

Таблица
7.7. Расчет производства цельномолочной
продукции по укрупненным периодам
(трехлетиям).

Укрупненные периоды	Сумма цельномолочной продукции в пересчете на молоко	Среднегодовое производство цельномолочной продукции в пересчете на молоко
1995-1997	2358	786,0
1998-2000	2938	979,3
2001-2003	2796	932,0
2004-2006	3398	1132,7

Алгоритм
расчета:

801+744+813
= 2358; 2358/3=786,0

952+1032+954=2938;
2938/3=979,3 и т.д.

Из
последнего столбика таблицы 7.7 и рисунка
7.3 более четко видна тенденция к росту
производства цельномолочной продукции.

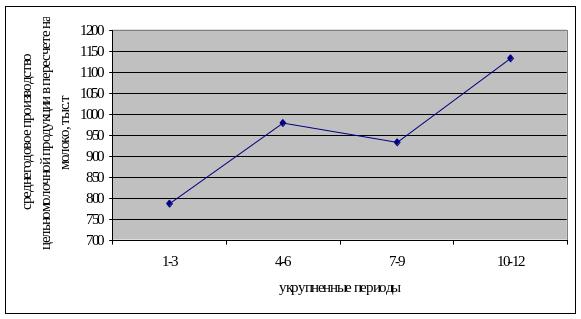
Рисунок
7.3. График ряда, выровненного по укрупненным
интервалам

Второй
способ
заключается в последовательном расчете
средних уровней за выбранный лаг времени,
передвигая этот лаг

на
1 интервал по времени t.
Величину лага L
выбирают произвольно в зависимости от
длины анализируемого ряда: L
= 2, 3, 4, …, n
. Например, мы выберем трехлетний лаг.
И тогда выровненный ряд можно представить
в следующей таблице (7.8).

Алгоритм расчета:

801+744+813=2358; 2358/3=786,0

744+813+952=2509; 2509/3=836,3

813+952+1032=2797;
2797/3=932,3 и т.д.

В настоящее время
в основном используют третий метод,
который рассмотрим в следующем вопросе.

Таблица
7.8 – Расчет трехлетней скользящей
средней.

Годы	Цельномолочная продукция в пересчете на молоко, тыс. т	Сумма цельномолочной продукции в пересчете на молоко по трехлетиям, тыс. т	Трехлетняя скользящая средняя, тыс. т
1995	801	–	–
1996	744	–	–
1997	813	2358	786,0
1998	952	2509	836,3
1999	1032	2797	932,3
2000	954	2938	979,3
2001	963	2949	983,0
2002	906	2823	941,0
2003	927	2796	932,0
2004	992	2825	941,7
2005	1122	3041	1013,7
2006	1284	3398	1132,7

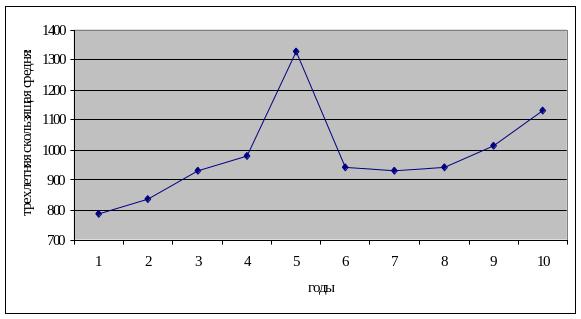
Рисунок
7.4. График ряда, выровненного по скользящей
средней

В
4. Тренд.
Аналитическое выравнивание ряда.
Прогнозы по тренду.

Самые
точные результаты выравнивания ряда
динамики дает аналитическое выравнивание,
с помощью которого строят математическое
уравнение, наилучшим образом описывающее
тенденцию изменения показателя.

Понятие
об уравнении тенденции динамики ввел
в 1902 году английский ученый Р.Гукер. Он
предложил называть такое уравнение
трендом (the
trend).

Под
трендом
понимают уравнение линии во времени,
вдоль которой расположена ломаная ряда
динамики.

Этапы построения
тренда:

1.
Выявляют этапы развития явления (спады,
подъемы, однородные участки и т.д.).

2.
Анализируют показатели ряда динамики
на этих этапах и выбирают вид уравнения
(вид тренда).

3.
Вычисляют параметры тренда, используя
метод наименьших квадратов.

4.
Оценивают адекватность уравнения
развитию анализируемого показателя,
оценивая колеблемость фактических
уровней ряда вокруг теоретических, т.е.
вычисленных по тренду.

Рассмотрим
3-ий этап на простейшем примере, когда
трендом является уравнение прямой
линии. Будем искать уравнение в виде:

(7.11)

где
t
– параметр времени; Y_t
– соответствующие времени уровни ряда,
Ŷ_t–
выровненные уровни ряда, т.е. вычисленные
по тренду.

Исходную
информацию и расчетные показатели
представим в виде таблицы 7.9.

Используя
метод наименьших квадратов, построим
систему уравнений:

(7.12)

Таблица
7.9. Схема таблицы для расчета параметров
тренда

t	Yi	t2	Y∙t	Ŷ
1 2 3 … n	Y1 Y2 Y3 … Yn			Ŷ Ŷ
t	Y	t2	(Y∙t)	ΣŶ

Решение
этой системы позволит найти значения
параметров уравнения. Если уравнение
построено качественно, то Y_i
= Σ Ŷ_t
.

Эти
расчеты можно упростить, если иначе
производить номерацию параметра t.
Ее нужно произвести следующим образом:
начало отсчета должно находиться в
середине анализируемого ряда. Если
количество точек нечетное, то в середине
ряда t
ставим 0; если количество точек четное,
то нуль выбрасывается. К началу ряда
счет идет со знаком «–», к концу – со
знаком «+», тогда t
становиться равной 0 (т.е. t=0).

Таблица
7.10. Схема номерации уровней ряда от
середины ряда

t для нечетного количества уровней ряда	t для четного количества уровней ряда
–к	–к
…	…
–2	…
–1	–2
0	–1
+1	+1
+2	+2
…	…
+к	+к
кi=0	кi=0

Тогда
в системе нормальных уравнений (7.12)
исчезнут слагаемые, в которые входит
сумма t
(Σt=0),
т.е. мы получим упрощенную систему

(7.13)

где
n
– количество точек анализируемого
ряда.

Отсюда:

(7.14)

(7.15)

Параметр
а₁
соответствует абсолютному приросту за
единицу периода времени.

Тенденции
или тренды могут быть выражены в виде
кривых. Это могут быть: парабола, ветка
гиперболы, экспонента или показательная
кривая, логарифмическая линия и т.д.
Виды трендов в виде кривых и их построение
рассмотрим ниже.

Прогноз
по тренду.
Используя уравнение можно построить
точечный прогноз на последующие периоды
времени, подставляя в уравнение тренда
(7.11) номера t,
следующие за последним фактическим
номером, используемым при построении
тренда. Например:

Таблица
7.11. Схема расчета прогноза при различной
номерации показателей ряда динамики

Номерация t от начала ряда	Номерация t от середины ряда
1	-6
2	…
…	-1
11	+1
прогноз 12	+2
прогноз 13	…
прогноз 14	+6
прогноз 15	прогноз 7
и т.д.	прогноз 8

Параметры
а₀
и а₁
в уравнении тренда, построенных различным
способом нумерации t, будут отличаться,
а прогнозы будут совпадать.

Оценка
точности тренда.
В экономическом анализе необходимо
оценить силу разброса фактических точек
вокруг расчетных (трендовых). Это
оценивается по величине остаточного
среднеквадратического отклонения и
коэффициенту вариации:

(7.16)

где
n
– число уровней ряда; m
– число параметров в уравнении тренда
(например, для прямой m=2,
для параболы m=3).

(7.17)

г
де
Y_i
– средний
уровень ряда.

Чем
меньше значения σ_ост.
и V,
тем лучше тренд отражает тенденцию
изменения показателя.

Имея оценку качества
тренда, производят оценку качества
прогноза на перспективу.

Для
точечного прогноза по тренду, также как
и для выборочного наблюдения, необходимо
оценить среднюю ошибку прогноза.

Для
линейного тренда средняя ошибка прогноза
рассчитывается:

(7.18)

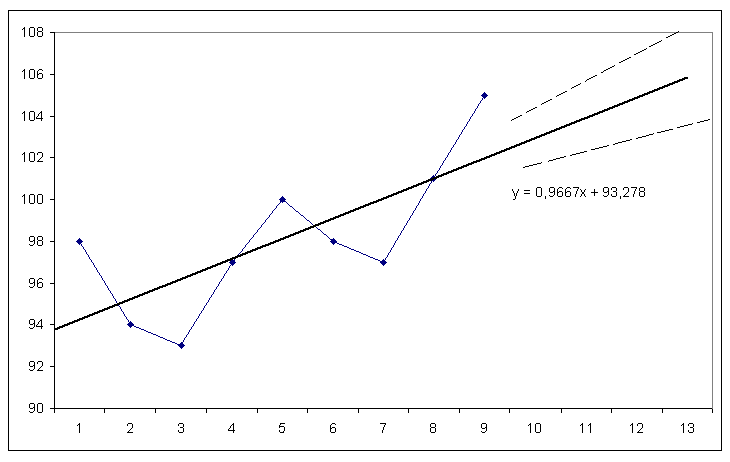
Рисунок
7.5. Точечное и интервальное прогнозирование

Доверительный
интервал или предельная ошибка прогноза
равна средней ошибке умноженной на
коэффициент доверия t-Стьюдента,
при доверительных вероятностях p=0,90;
0,95; 0,99. Строчку в таблицах находим по
числу степеней свободы тренда n
– m
.

В
5. Сезонные колебания в рядах динамики

Если
ряд динамики насчитывает достаточное
количество уровней, например 100, то можно
обнаружить колебания, которые повторяются,
т.е. наличие регулярных спадов и подъёмов.
Такие макроэкономические колебания
называются циклическими.
Такого вида колебания рассматриваются
в курсе макроэкономики, когда оценивают
динамику экономического развития
отдельных государств.

Внутри
годичные колебания, имеющие регулярный
характер, т.е. повторяющиеся из года в
год, называются сезонными
.

Сезонные
подъёмы и спады в производстве снижают
равномерность, устойчивость технологического
процесса и реализации продукции и должны
учитываться при планировании производства.

Сезонные
колебания показателя могут накладываться
на тенденцию роста или спада фактора,
а могут наблюдаться при постоянной
случайной колеблемости. В зависимости
от этого графики могут иметь следующий
вид:

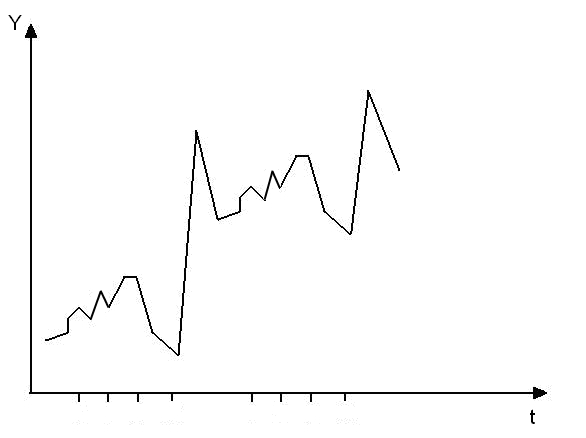
Рисунок
7.6. Наличие тенденции, случайных и
сезонных колебаний

На
рисунке хорошо видны спады в четвертом
квартале и подъемы в первом. В остальные
периоды наблюдается случайная колеблемость
при наличии тенденции к росту показателя.

На
рисунке 7.7. видно, что изменение показателя
не имеет тенденции ни к росту, ни к
снижению. Однако видна четко выраженная
сезонная колеблемость показателя, т.е.
есть периоды «впадин» и «подъемов».

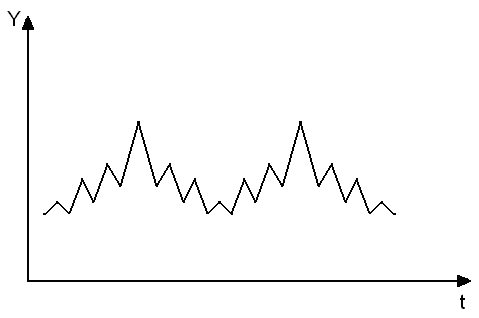
Рисунок
7.7. Наличие сезонных и случайных колебаний

Чаще
всего степень сезонных колебаний
определяют по величине индекса сезонности.
Различают индивидуальные индексы
сезонности и средние, с учётом тренда
и без его наличия.

Если
тренд отсутствует, то индивидуальный
индекс сезонности может быть вычислен
как отношение величины месячного
(квартального) уровня к среднегодовому:

(7.19)

Средний
индекс сезонности равен сумме
индивидуальных индексов сезонности,
делённой на количество сезонов n.
Так как анализ может проводиться за
несколько полных лет и один (последний)
неполный год, то число n
будет различным для той части времени,
где учитываются только полные годы и
для той, где есть дополнительно значения
ряда за неполный год.

(7.20)

В
сельском хозяйстве анализ сезонных
колебаний на основе данных поквартального
учёта несколько ухудшает показатель
сезонности, потому что времена года
(сезоны) не совпадают с календарными
периодами. Поэтому исследование наличия
сенных колебаний лучше
проводить на основании данных помесячного
учета.

Если
анализируемый показатель имеет не
только сезонные колебания, но и достоверную
тенденцию (тренд), то в знаменателе
берётся показатель ряда, взятый по
тренду:

(7.21)

Оценка
индекса сезонности осуществляется по
среднему линейному или среднеквадратическому
отклонению для каждого года. Если
коэффициенты сезонности (линейный и
среднеквадратический) увеличиваются,
то это свидетельствует об усилении
сезонных колебаний; если уменьшаются,
то наоборот.

Среднее
линейное отклонение коэффициента
сезонности рассчитывают по формуле:

=

(7.22)

Среднеквадратическое
отклонение коэффициента сезонности
рассчитывают по формуле:

=

(7.23)

где
n – число сезонов.

Чем
меньше значения этих показателей, тем
меньше сезонная колеблемость и выше
стабильность показателя.

В
6. Модели рядов с учетом тенденции и
сезонности.

Тенденцию
ряда и наличие сезонности можно
представить в виде двух различных
моделей:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Была ли эта статья полезной?

Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.

Как рассчитать темп роста: формула

Что называют снижением темпа роста цен?
Подробнее

Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.

Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.

Как рассчитать темп роста в процентах – формула:

ТР = П_т / П_б х 100%,

где П_к и П_б – показатели значений текущего и базового периодов.

Узнайте, может ли темп роста быть отрицательной величиной.

Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:

1. ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;

2. ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;

3. ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.

Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:

Объем выпуска в тыс. руб.	Расчет (Пт / Пб х 100%)
2017 (Пб)	2018 (Пт)
600	800	133,3%
600	600	100%
600	400	66,7%

Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.

Узнайте, чем отличается темп роста от темпа прироста.

Как рассчитать цепные темпы роста

Рассмотрим пример расчета базисного и цепного темпов роста:

Период	Объем в тыс.руб.	Темп роста в %
базисный	цепной
1 кв.	300	100	–
2 кв.	310	103,3 (310 / 300)	103,3 (310 / 300)
3 кв.	280	93,3 (280 / 300)	90,3 (280 / 310)
4 кв.	360	120 (360 / 300)	128,6 (360 / 280)

Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).

Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.

Как рассчитать темпы прироста

Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:

∆ ТР = (П_тек – П_баз) / П_баз х 100%

Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:

∆ ТР = (П_тек – П_пр.п) / П_{пр. п} х 100%.

Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.

Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:

Период	Темпы прироста
базисные	цепные
1 кв.	–	–
2 кв.	3,3% (103,3 – 100) или ((310 – 300) / 300 х 100)	3,3% (103,3 – 100) или ((310 – 300) / 300 х 100)
3 кв.	– 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100)	-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100)
4 кв.	20% (120 – 100) или (( 360 – 300) / 300 х 100)	28,6% (128,6 – 100) или ((360 – 280) / 280 х 100)

Анализируя результаты вычислений, экономист может сделать вывод:

• Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;

• Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.

Как рассчитать средний темп роста

Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.

Показатель	Значение в %	Расчет
Средний темп роста (базисный)	105,5	(103,3 + 93,3 + 120) / 3
Средний темп прироста (базисный)	5,5	(3,3 – 6,7 + 20) / 3
Средний темп роста (цепной)	107,4	(103,3 + 90,3 + 128,6) / 3
Средний темп прироста (цепной)	7,4	(3,3 – 9,7 + 28,6) / 3

Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.

Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право – работа с недвижимостью. договорная работа, наследственное право, банкротство.