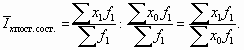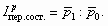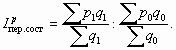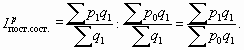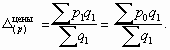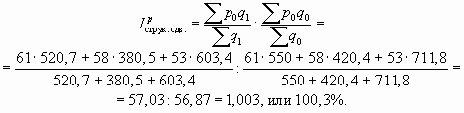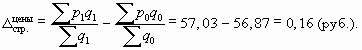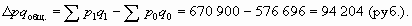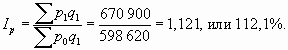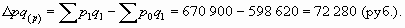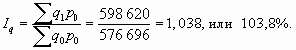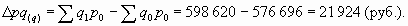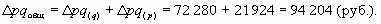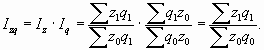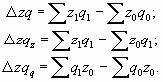Покажем все нюансы, почему новости СМИ о ценах недвижимости неинформативны. Докажем, что заголовки об изменении цен “на 5%” — не более, чем развлекательный жанр. Как и рейтинги жилых комплексов или районов по стоимости метра. Дочитайте до конца, и будете иначе смотреть на такие публикации.
Введение
Средневзвешенная цена квадратного метра – привычный показатель в аналитике недвижимости. Однако, многие не задумываются о сложностях, которые за ним скрываются.
В рамках данной статьи мы приведем примеры, когда использование среднего может вызвать проблемы, а также способы их решения. Но, сначала, обсудим базовые вещи.
Среднее взвешенное или среднее арифметическое
Среднее взвешенное – это характеристика массива данных.
В рамках аналитики рынка недвижимости среднее взвешенное применяется чаще всего для расчёта цены метра, где в качестве веса используются площади лотов из прайс-листов. Далее в статье мы будем иметь в виду именно данные из прайс-листов, хотя все суждения справедливы и для других наборов данных, например, для проданных объектов недвижимости.
Среднее арифметическое – это частный случай среднего взвешенного, просто весом является количество элементов (например, средняя стоимость лота по прайс-листу – это среднее взвешенное, где весом является количество лотов).
Нельзя сказать, что одно лучше другого. Выбор между средним взвешенным и средним арифметическим – это выбор аналитика, который работает с данными.
Проблемы начинаются тогда, когда мы сравниваем два значения среднего взвешенного между собой. Далее примеры.
Пример: сравнение цены метра на рынке от месяца к месяцу
Практически во всех аналитических материалах и новостях сообщается об изменении цены метра. Допустим, нам сообщают, что она выросла на 0,5%. При кажущейся очевидности, это не дает нам никакой полезной информации, потому что, скорее всего, изменилась структура данных.
Дело в том, что мы не можем однозначно сказать, что из перечисленного произошло:
-
вышел ли в продажу новый объем лотов по цене выше рынка;
-
ушли ли из продажи дешевые лоты;
-
подорожали или подешевели квартиры, которые так и не были проданы за месяц;
-
или любая комбинация из перечисленных выше пунктов.
Но и это ещё не всё. Допустим за месяц на рынке не появились новые лоты и не ушли из продажи старые (то есть в экспозиции остались все те же квартиры). Тогда “рост на 0,5%” опять не дает нам ценной информации, потому что:
-
могли подорожать все квартиры равномерно;
-
могли подорожать студии, а крупные квартиры подешеветь;
-
в одной локации могло быть подорожание, а в другой – удешевление.
Прирост на 0,5% к цене метра приобретает смысл, если смотреть на изменение цены метра по узкой выборке, например только студии в проектах бизнес-класса Москвы.
В таком случае +0,5% будет означать, что именно такой продукт подорожал, но всё равно остаётся вопрос в равномерно ли произошёл рост в разных локациях.
Примере даёт понять, что сравнивать два средних можно только если они рассчитаны на сопоставимых наборах данных. Бессмысленно сравнивать вчерашнюю цену студий с сегодняшней ценой трёхкомнатной квартиры.
Пример: анализ инвестиционной привлекательности жилых комплексов
Ещё одна из интересных тем аналитических материалов, кто сколько заработал на основе данных об изменении цен в жилых комплексах.
Но рост цены в одном жилом комплексе на 20% за год не означает, что инвесторы эти 20% заработали.
Рост цены метра в жилом комплексе может получиться из-за продажи дешевых лотов, тогда мы опять сравниваем цены совершенно разных квартир в ЖК.
Чтобы точно посчитать сколько мог заработать инвестор, надо сравнить стоимость конкретной квартиры на момент покупки и через год.
Такой точечный анализ сложно делать без специального программного обеспечения, поэтому разумно использовать среднюю цену метра. Аналитику остается только правильно сделать выборки данных, которые затем будут сравниваться через среднюю цену метра.
Тогда по изменению средней цены, например, студий площадью 20-30 кв.м. уже можно сделать какие-то выводы.
Пример: сравнение двух ЖК по цене метра
И ещё частая задача – сравнение жилых комплексов, где одним из критериев является средняя цена метра.
Если один ЖК дороже другого на 10%, то это опять может ничего не значить.
Для корректного анализа нужно ответить на вопросы: конкурирующие ли это проекты по продуктовым характеристикам? Сравниваем ли мы похожие лоты в жилых комплексах?
Мы снова должны решить задачу правильного выбора данных для сравнения.
Что можно сделать на практике
Сравниваем одни и те же лоты
Допустим мы работаем с двумя прайс-листами ЖК комфорт-класса в Новой Москве за два разных месяца, и нам надо проанализировать изменение цены метра. Идеально – сравнить каждый лот и сделать выводы, но это трудоемко.
Решением может являться разделение прайс-листов на три массива:
-
Ушедшие лоты из прайс-листа за месяц;
-
Новые лоты в прайс-листе за месяц;
-
Лоты, оставшиеся в экспозиции.
Можно посчитать отдельно цену метра для новых лотов, отдельно цену метра лотов, которых больше нет в прайс-листе.
Что касается лотов, которые присутствуют в экспозиции в обоих месяцах – это уже более подходящие наборы для сравнения средней цены метра. Анализ будет более точным, так как мы сравниваем одни и те же квартиры.
Ищем, кто повлиял на цену сильнее всех
Допустим, если цена на рынке снизилась на 1%, то это падение будет складывается из изменений цены метра в каждом жилом комплексе.
Можно найти топ-ЖК, в которых цена метра выросла, и топ-ЖК, в которых цена метра снизилась.
Это не даст абсолютного понимания рынка, но позволит перейти к осознанной аналитике произошедшего уже в конкретных жилых комплексах.
Например, в рамках одного ЖК можно разбить лоты по комнатности или по диапазонам площадей, и также составить топ по тому, какие квартиры двигали цену всего ЖК вверх, а какие вниз.
Детализация через визуализацию
Если сопоставлять среднюю взвешенную цену метра в рамках одного ЖК от месяца к месяцу, то из-за того что из прайс-листов уходят проданные лоты и появляются новые, изменение средней цены метра по ЖК может давать ложные сигналы. Если из прайс-листа ушли дорогие лоты, то цена средневзвешенная цена метра в ЖК увеличится, хотя цены остались прежними.
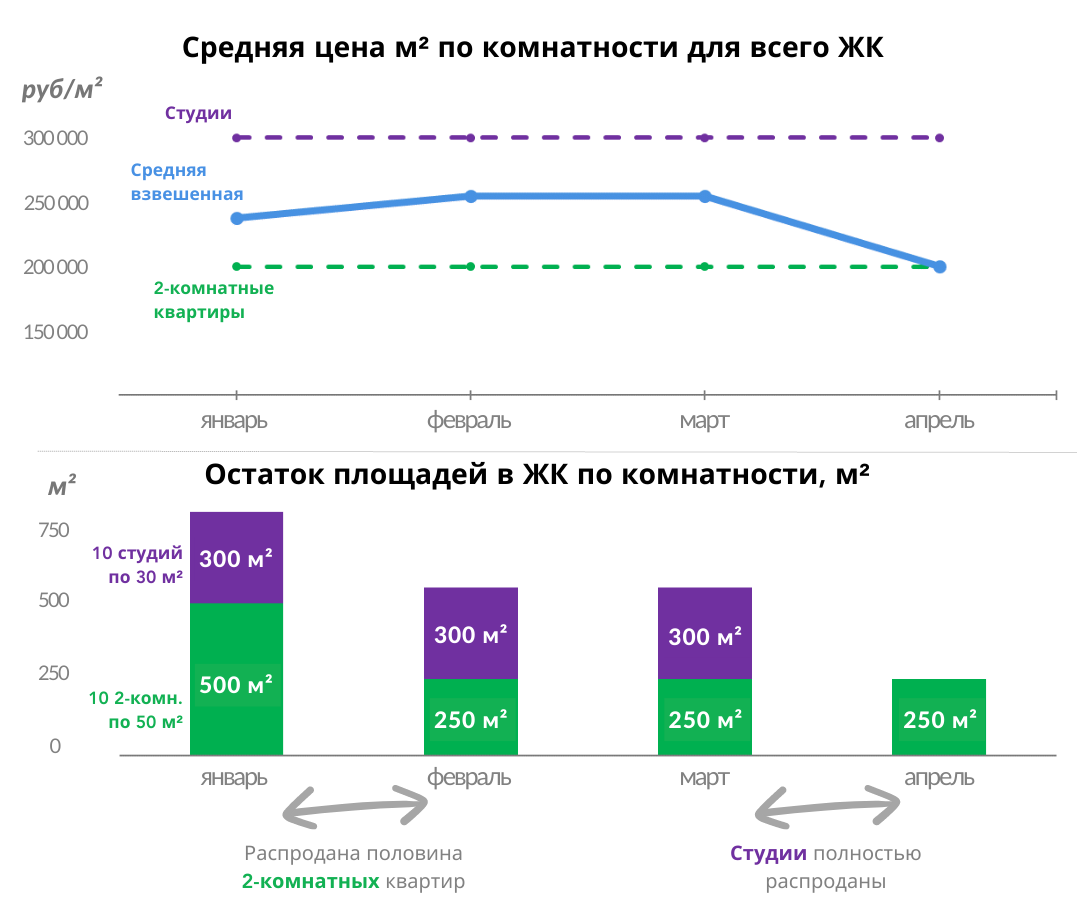
Чтобы всё было прозрачно, поможет график изменения цены метра с детализацией по всем диапазонам площадей в жилом комплексе, или по комнатности.
На графике цена метра студий и 2-комнатных квартир остаются горизонтальными, при том что синяя линия средневзвешенной цены метра во всем жилом комплексе то выше то ниже.
Это просто объяснить – в жилом комплексе есть 10 двухкомнатных квартир (по 50 кв.м. каждая) и 10 студий (по 30 кв.м. каждая).
За месяц было продано пять 2-комнатных квартир. При этом цена метра по комнатностям не изменилась, но изменилась цена метра во всем жилом комплексе – она выросла.
Если в апреле будут проданы все студии, то средняя взвешенная цена метра в жилом комплексе снизится, хотя изменения цен тоже не происходило.
Простая визуализация позволяет видеть все движения по узким однородным выборкам, дает возможность видеть точные изменения цен.
Выводы
Мы рассмотрели основные примеры, когда у аналитика могут возникнуть сложности при работе со средневзвешенной ценой метра, и пути их решения.
Главное, о чем нужно помнить – сравнение среднего взвешенного возможно только в похожих по характеристикам или структуре выборках (студии к студиям, бизнес-класс к бизнес-классу, квартиры 50 кв.м. к аналогичным по метражу и т.п.).
Разнородные данные сравнивать некорректно.
Именно поэтому основной задачей аналитика при сопоставлении средних цен квадратного метра является поиск и создание таких выборок с последующим их анализом.
10.5. Анализ динамики среднего уровня показателя
На формирование среднего уровня качественного показателя оказывают влияние два фактора: во-первых, изменение индивидуальных значений самой индексируемой величины в отчетном периоде по сравнению с базисным, и, во-вторых, изменение структуры исследуемой совокупности (уменьшение или увеличение доли единиц с более низким или более высоким уровнем этого показателя). Например, на динамику средней цены влияют изменения индивидуальных уровней цен и различия в структуре продаж отчетного периода по сравнению с базисным; на формирование среднего уровня фондоотдачи – изменения фондоотдачи отдельных видов основных фондов и доли основных фондов с более высоким (низким) уровнем фондоотдачи в общей их совокупности (структурный фактор).
Относительное изменение среднего уровня качественного показателя характеризуется с помощью системы индексов переменного, постоянного состава и индекса структурных сдвигов, позволяющих оценить влияние каждого фактора на его динамику.
Покажем общую схему построения системы индексов, характеризующих динамику среднего уровня качественного показателя. Индекс переменного состава отражает изменение среднего уровня качественного показателя за счет двух факторов. Пусть х – индексируемая величина, f – вес индекса. В общем виде этот индекс рассчитывается как отношение среднего уровня показателя в отчетном периоде к среднему уровню показателя в базисном периоде. Индекс переменного состава для любых качественных показателей может быть записан следующим образом:
Индекс постоянного (фиксированного) состава показывает, как в среднем изменилось значение качественного показателя у единиц совокупности при одинаковой фиксированной ее структуре. В общем виде его можно записать следующим образом:
Формула индекса влияния структурных сдвигов, представляющего собой отношение средних величин рассматриваемого качественного показателя, рассчитанных при структуре совокупности отчетного и базисного периодов при базисном уровне качественного показателя, выглядит следующим образом:
Поскольку индекс переменного состава показывает изменение исследуемого явления за счет всех факторов, то между индексами существует следующая взаимосвязь:
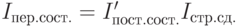
Так, при изучении изменения средней цены товара (например, продаваемого в разных регионах) индекс переменного состава можно записать следующим образом:
Подставляя вместо P0 и P1 выражения для расчета средних уровней цен товара отчетного и базисного периодов, получим его развернутую формулу
На его величину оказывают влияние два фактора: изменение цены товара в каждом регионе и структуры продаж. Абсолютное изменение среднего уровня цены товара за счет двух факторов покажет разность между числителем и знаменателем рассматриваемого индекса:
Индекс цен постоянного (фиксированного) состава показывает изменение средней цены товара только за счет изменений цен в каждом регионе. Индекс цен постоянного состава имеет вид
Абсолютное изменение среднего уровня цены за счет изменения индексируемой величины покажет разность между числителем и знаменателем данного индекса
Индекс структурных сдвигов позволяет оценить влияние на формирование среднего уровня цены изменений в структуре продаж товара:
Абсолютное изменение среднего уровня качественного показателя (в данном случае средней цены) за счет структурных сдвигов
Пример 10.6. В таблице приведены цены и объемы продаж товара “А” в трех регионах.
| Регион | Цена товара “А”, руб. за кг | Объем продаж товара “А”, тыс. кг | ||
|---|---|---|---|---|
| базисный период, p0 | отчетный период, p1 | базисный период, q0 | отчетный период, q1 | |
| I | 61 | 69 | 550,0 | 520,7 |
| II | 58 | 65 | 420,4 | 380,5 |
| III | 53 | 57 | 711,8 | 603,4 |
Индекс цен переменного состава равен
Общее измерение средней цены в абсолютном выражении
За счет действия двух факторов средняя цена увеличилась на 11,1%, или на 6,31 руб.
Для определения влияния первого фактора (цен в каждом регионе) на динамику средней цены исчислим индекс цен постоянного состава:
Тогда влияние первого фактора в абсолютном выражении можно определить как
Таким образом, в результате изменения цен товара “А” в отдельных регионах его средняя цена увеличилась на 10,8%, или на 6,15 руб.
Влияние на анализируемый показатель структурных изменений в структуре продаж товара “А” покажет индекс структурных сдвигов
В абсолютном выражении
В результате изменения структуры продаж товаров по регионам средняя цена возросла на 0,3%, или 16 копеек.
Проверим взаимосвязь индексов и абсолютных приростов:
10.6. Факторный анализ
Как отмечалось выше, индексы используются не только для характеристики интенсивности изменения социально-экономических явлений, но и для выявления влияния на этот процесс различных факторов. Так, например, на основе индексов определяют степень влияния изменения себестоимости продукции и структуры производства на динамику затрат на производство продукции; производительности труда и затрат рабочего времени – на изменение объема продукции и т.д.
Покажем это по данным примера 10.2 о ценах и объеме продаж молочной продукции (см. табл. в примере).
Пример 10.7. Проанализируем прирост товарооборота под влиянием двух факторов: изменения цен на товары и объема их продаж. Общий индекс товарооборота равен
Товарооборот в относительном выражении увеличился на 16,3%. Найдем абсолютный прирост товарооборота за счет двух факторов – разность между числителем и знаменателем этого индекса:
Как видим, товарооборот возрос на 94 204 руб. (или 16,3%) за счет двух факторов.
Общий индекс цен, как отмечалось выше, показывает относительное изменение товарооборота под влиянием цен:
Разность между числителем и знаменателем этого индекса позволяет оценить влияние цен на динамику товарооборота в абсолютном выражении:
Таким образом, за счет роста цен на молочную продукцию товарооборот увеличился на 72 280 руб., или на 12,1%.
Общий индекс физического объема товарооборота отражает в относительном измерении влияние второго фактора – количества проданных товаров на динамику изучаемого показателя:
Абсолютный прирост товарооборота за счет изменения объема продаж молочной продукции определим как разность между числителем и знаменателем этого индекса
Произведение индексов цен и физического объема товарооборота равно общему индексу товарооборота:
lpq= lp x lq = 1,121 * 1,038 = 1,163 или 116,3%
Если сложить абсолютные изменения товарооборота за счет первого и второго фактора, то получим его общее абсолютное изменение:
Аналогично проводится анализ изменения затрат на производство продукции под воздействием двух факторов: изменения себестоимости продукции и объемов производства. Относительное влияние отражают индексы
Абсолютное изменение затрат на производство за счет отдельных факторов рассчитывается следующим образом:
Взаимосвязь абсолютных изменений определяется уравнением
Индексный
метод – один из самых распространенных методов статистического анализа
экономических явлений. С помощью индексов изучаются народное хозяйство в целом
и его отдельные отрасли, а также деятельность предприятий, объединений, фирм,
хозяйств и др.; выявляется динамика развития социально-экономических явлений,
анализируется выполнение планов или норм; определяется влияние отдельных
факторов на общий результат, вскрываются резервы производства; проводятся
территориальные и международные сопоставления экономических показателей.
Индексом
в статистике называется относительный показатель, характеризующий соотношение
во времени, по сравнению с планом или в пространстве уровней социально-экономических
явлений. Так как индекс – относительный показатель, то он всегда получается при
соотношении двух величии: отчетной (или текущей), т. е. сравниваемой, и
базисной, т. е. той, с уровнем которой сравнивается отчетная величина. Если за
базу сравнения берется уровень явления за какой-то прошлый период времени,
получают динамические индексы; если за базу сравнения берется уровень явления
на другой территории, получают территориальные индексы, а если за базу
сравнения берется какой-либо нормативный уровень, получают индексы выполнения
плана, индексы выполнения норм и т. д.
В
формулах, системах уравнений, экономико-математических моделях текущие данные
помечаются единицей, стоящей чуть ниже буквенного обозначения величины.
Как
и всякая относительная величина, индексы выражаются в виде коэффициентов, если
за основание принимается единица, или в виде процентов, если за основание
принимается сто.
Социально-экономические
явления, изучаемые статистикой, обычно состоят из многих элементов. Так,
валовой выпуск продуктов и услуг включает стоимость конечных товаров и услуг,
созданных всеми общественно организованными видами экономической деятельности и
во всех отраслях экономики. Другими словами, валовой выпуск продуктов и услуг
состоит из многих отдельных видов продуктов и услуг.
Индексы
рассчитываются как для отдельных элементов сложного явления, так и для всего
сложного явления в целом. В первом случае они называются индивидуальными и
обозначаются латинской буквой
, а во второй –
общими и обозначаются
. К индивидуальным
индексам относятся индексы, характеризующие изменение выпуска одного
какого-либо вида продукции (индексы выплавки стали, добычи калийных удобрений,
производства телевизоров и др.), индексы, характеризующие изменение цены
какого-либо товара (велосипедов, цемента, говядины и др.), себестоимости
отдельного изделия и т.д.
К
индексам, исчисленным для всего сложного явления, то есть к общим, относятся
индексы, характеризующие динамику выпуска всей продукции предприятия, отрасли и
др., динамику цен группы товаров, или всех товаров, или набора
продовольственных и непродовольственных товаров и услуг, входящих в «потребительскую
корзинку», динамику себестоимости ряда изделий и т. д.
Общие
индексы используются для сопоставления непосредственно несоизмеримых,
разнородных явлений. Например, с помощью общих индексов можно охарактеризовать
динамику выпуска продукции всей промышленности или динамику объемов всей
выпускаемой продукции на мебельной фабрике, изготавливающей различные виды
продукции: столы, кресла, диваны, шкафы. Однако нельзя просто сложить объемы
продукции различных видов за два периода и отнести эти суммы одну к другой.
Такое суммирование бессмысленно не только из-за различных единиц измерения
(тонны, штуки, метры и др.), но также из-за того, что каждый вид продукции
имеет свое назначение и произведен с разными затратами средств и общественно
необходимого времени.
Чтобы
сделать сопоставимыми несоизмеримые явления (или их элементы), нужно выразить
их общей мерой; стоимостью, трудовыми затратами и т. д. Эта задача решается
построением и расчетом общих индексов. Основной формой общих индексов являются
агрегатные индексы.
Агрегатный
индекс состоит из двух элементов: индексируемых величин, изменение которых
должен отразить индекс, и показателей, которые служат соизмерителями (весами).
Произведение
каждой индексируемой величины на соизмеритель (вес) должно давать определенную
экономическую категорию.
Значение
индексируемой величины всегда изменяется: отчетное значение сопоставляется с
базисным. Конкретное название индекса дается всегда по индексируемой величине.
Например, если индексируется цена, то получают индекс цен, если индексируется физический объем,
получают индекс физического объема и т. д.
Показатель-соизмеритель
(вес) выполняет функцию веса по отношению к индексируемой величине. Значение
соизмерителя (веса) в конкретном индексе принимается одинаковым в числителе и
знаменателе, чтобы исключить влияние соизмерителя на изменение индексируемого
показателя. Веса индексов могут быть выражены в стоимостных, трудовых и других
единицах измерения, а также в виде относительных величин структуры. При
построении агрегатных индексов важно правильно выбрать веса индексов. Они
должны выбираться с учетом сущности исследуемого социально-экономического
явления, чтобы сохранить экономический смысл индекса и получить возможность на
его основе исчислять абсолютные суммы экономического эффекта.
В
зависимости от содержания и характера индексируемой величины различают индексы
количественных (объемных) показателей и индексы качественных показателей.
Количественные (экстенсивные) показатели характеризуют общий, суммарный размер
того или иного явления, например, количество (физический объем) продукции в
натуральном выражении, численность работников, общие затраты времени на
произведенную продукцию, размер посевной площади и т. д. Качественные
(интенсивные) показатели характеризуют размер признака в расчете на единицу
совокупности: цена единицы продукции (товара), себестоимость единицы продукции,
затраты рабочего времени па единицу продукции (трудоемкость единицы продукции),
выработка продукции на одного работающего, расход материала (топлива) на
единицу продукции, урожайность культуры в расчете на один гектар и т. п. Как
правило, качественные показатели представляют собой либо средние значения, либо
относительные величины.
Существует
правило построения агрегатных факторных индексов, в соответствии с которым в
индексах качественных показателей весами выступают показатели отчетного
периода, а в индексах количественных показателей — базисного периода.
Соответствующие
количественные (объемные) и качественные показатели тесно связаны друг с другом.
В общем виде эта взаимосвязь выражается в том, что произведение качественного
показателя на связанный с ним количественный показатель дает новый показатель,
другую экономическую категорию. Например, если перемножить цену одного изделия
(
, качественный
показатель) на количество этих изделий (
, количественный
показатель), то получим общую стоимость данных изделий или товарооборот (
, новый
показатель); произведение удельного расхода материала
на количество единиц продукции
представляет собой
общий расход материала (
, новый
показатель); произведение урожайности культуры на ее посевную площадь дает
валовой сбор этой культуры (новый показатель) и т. д. Эта взаимосвязь между
количественными и качественными показателями справедлива при построении и
исчислении их агрегатных индексов.
Например,
произведение агрегатного индекса цен
на агрегатный индекс физического объема
равно агрегатному индексу стоимости продукции
(товарооборота)
.
Агрегатный
индекс цен
определяется по формуле:
Агрегатный
индекс цен характеризует, как изменились в среднем цены на различные виды
продукции, включенные в расчет общего индекса цен.
Агрегатный
индекс физического объема
характеризует, как изменился в среднем общий
объем продукции по анализируемому перечню. Он определяется по формуле:
Индекс
стоимости продукции (товарооборота) определяется по формуле:
Индекс
стоимости продукции характеризует изменение фактической стоимости произведенной
или реализованной продукции или же размера товарооборота по анализируемой
совокупности.
Взаимосвязь
индексов может быть представлена выражением:
Используя
эти формулы, можно по двум известным индексам определить третий.
Агрегатный
индекс является основной, но не единственной формой общего индекса. Общий
индекс может быть исчислен и как средняя величина индивидуальных индексов. Эта
средняя может быть рассчитана как средняя арифметическая и как средпяя
гармоническая. Как одна, так и другая средняя выводятся из агрегатных индексов
и дают результаты, тождественные этим индексам. Выбор формы индекса зависит от
характера исходных данных. Если известны значения индексируемого показателя и
веса в отчетном (текущем) и базисном периодах, то пользуются агрегатной формой
индексов. Если отсутствуют значения индексируемого показателя или веса в
отчетном или базисном периодах, по известны изменения индексируемого показателя
или веса по отдельным единицам изучаемой совокупности, то пользуются формой
средних индексов.
При сравнении уровней
средних величин отчетного и базисного периодов получают индекс, который в
статистике называют индексом переменного состава. Так, например, индекс
себестоимости переменного состава исчисляется по формуле:
На индекс переменного
состава (динамику средних величин) оказывают влияние два фактора: во-первых,
изменение уровней осредняемого признака (в нашем
примере изменение уровней себестоимости продукции по каждому из предприятий) и,
во-вторых, изменение долей единиц совокупности с различными значениями признака
(структурные сдвиги).
Индекс переменного состава
вычисляют и по такой формуле:
где
Индекс себестоимости
постоянного фиксированного состава рассчитывают по формуле:
или
Индекс
структурных сдвигов исчисляют по формуле:
или
Взаимосвязь индексов:
Вычитая из числителя
каждого из индексов приведенной системы знаменатель, получим разложение
абсолютного изменения (прироста) среднего уровня признака за счет
непосредственного изменения уровней осредняемого
признака (индивидуальных уровней себестоимости), так и за счет изменения
удельных весов (структурных сдвигов):
Задача 1
Динамика средних цен и
объема продажи на колхозных рынках города характеризуется следующими данными:
| Продукция | Продано продукции, тыс. кг | Средняя цена за 1 кг, тыс. р. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Колхозный рынок №1 | ||||
| Картофель | 4.0 | 4.2 | 6.4 | 7.6 |
| Капуста | 2.5 | 2.4 | 7.2 | 8.4 |
| Колхозный рынок №2 | ||||
| Картофель | 10.0 | 12.0 | 7.6 | 7.0 |
На основании имеющихся данных вычислите:
- Для колхозного рынка №1 (по двум видам продукции):
- а) индивидуальные индексы цен, физического объема и стоимости;
- б) общий индекс товарооборота;
- в) общий индекс цен;
- г) общий индекс физического объема товарооборота;
- Определите в отчетном периоде абсолютный прирост товарооборота и разложите по
факторам ( за счет изменения цен и объема продаж товаров). - Покажите взаимосвязь между исчисленными индексами.
- Для колхозных рынков вместе (по картофелю):
- а) индекс цен переменного состава
- б) индекс цен постоянного состава
- в) индекс влияния изменения структуры объема продаж картофеля на динамику средней цены
- Объясните разницу между величинами индексов постоянного и переменного состава.
- Определите общее абсолютное изменение средней цены картофеля в отчетном периоде
по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней
цен и за счет изменения структуры продаж картофеля. - Сформулируйте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Вычисление индивидуальных индексов товарооборота, цен и физического объема
Вычислим индивидуальные индексы цен:
Картофель:
Капуста:
Цены на картофель увеличились на 18,8%, а на капусту на 16,7%
Вычислим индивидуальные индексы физического объема:
Картофель:
Капуста:
Физический объем продаж картофеля увеличился на 5%, а физический
объем продаж капусты снизился на 4%.
Вычислим индивидуальные индексы стоимости продаж:
Картофель:
Капуста:
Стоимость продаж картофеля увеличилась на 24,7%, а капусты на 12%.
Вычисление общих индексов товарооборота, цен и физического объема
Общий индекс товарооборота можно вычислить по формуле:
где
– цена,
-количество проданной продукции
Общий индекс цен вычисляем по формуле:
Общий индекс физического объема
товарооборота:
Эти индексы связаны между собой формулой:
Таким образом, товарооборот увеличился на 19,4%, в том числе за счет
увеличения цен на 17,9%, за счет увеличения физического объема товарооборота на
1,3%
Разложение на факторы абсолютного прироста товарооборота
Абсолютный прирост товарооборота:
В том числе за счет изменения цены:
В том числе за счет изменения продажи товаров:
Абсолютные приросты связаны между собой формулами:
Таким образом, товарооборот
увеличился на 8,48 млн.р., в том числе за счет увеличения цен на 7,92 млн.р.,
за счет увеличения физического объема товарооборота на 0,56 млн.р.
Вычисление индесов средней цены переменного состава, постоянного состава и структурных сдвигов
Вычислим для 2-х колхозных
рынков по картофелю индекс цен переменного состава:
Вычислим индекс цен постоянного состава:
Вычислим индекс влияния изменения структуры объема продаж картофеля на
динамику средней цены:
Разница между индексами
переменного и постоянного состава заключается в том, что индекс переменного
состава равен соотношению средних уровней
цены, а постоянного характеризует изменение средней
цены за счет изменения только цен на каждом рынке.
Таким образом, средняя цена на рынках уменьшилась на 1.4%. Если бы на
обоих рынках структура продаж была одна и та же, средняя цена бы уменьшилась на 1.9% Увеличение доли более дорогого рынка в
структуре продаж увеличило среднюю цену на 0,4%.
Разложение на факторы абсолютного прироста средней цены
Определим общее абсолютное изменение цены картофеля:
Общее абсолютное изменение
цены за непосредственного изменения уровней цен картофеля:
Общее абсолютное изменение цены за счет изменения структуры продажи
картофеля:
Таким образом, средняя цена на
картофель снизилась на 0,11 тыс.р., в том числе за счет непосредственного
изменения уровней цен на 0,14 тыс.р. Увеличение доли рынка с более дорогим
картофелем увеличило результативный показатель на 0,03 тыс.р.
Задача 3
Имеются
следующие данные о выпуске одноименной продукции по трем цехам предприятия:
| Цех |
Произведено продукции, тыс.шт. |
Себестоимость производства единицы продукции, руб. |
||
| базисный период | отчетный период | базисный период | отчетный период | |
| 1 | 86 | 56 | 34.0 | 39.0 |
| 2 | 152 | 146 | 52.0 | 56.0 |
| 3 | 134 | 132 | 48.0 | 46.0 |
Определите:
- Индексы себестоимости переменного состава, постоянного состава и индекс
структурных сдвигов. - Абсолютное изменение средней себестоимости производства единицы продукции в
отчетном периоде по сравнению с базисным: а) общее; б) за счет изменения
себестоимости производства единицы продукции в отдельных цехах; в) за счет
изменения структуры произведенной продукции. - Установите
и проверьте взаимосвязи: а) между рассчитанными индексами; б) между
рассчитанными абсолютными изменениями. Поясните, в чем состоит структурный
сдвиг в производстве продукции в отчетном периоде по сравнению с базисным. - Сделайте
выводы.
Решение
Индексы себестоимости постоянного и переменного состава
Вычислим индекс себестоимости
переменного состава:
Вычислим индекс себестоимости постоянного состава:
Таким образом, средняя себестоимость в отчетном периоде увеличилась на
6%, при условии одинаковой структуры производства в цехах, себестоимость
увеличилась на 3,8%.
Индекс структурных сдвигов
Вычислим индекс влияния изменения структуры производства продукции на
динамику средней себестоимости:
Разница между индексами
переменного и постоянного состава заключается в том, что индекс переменного
состава равен соотношению средних уровней
себестоимости, а постоянного
характеризует изменение средней себестоимости за счет изменения только
себестоимости в каждом цеху. Структурный сдвиг состоит в изменение доли цехов с
более высокой (более низкой) себестоимостью.
Взаимосвязь между рассчитанными индексами будет следующая:
Индексы средней себестоимости в разностной форме
Определим общее абсолютное изменение себестоимости:
Общее абсолютное изменение
себестоимости за счет
непосредственного изменения уровня
себестоимости:
Общее абсолютное изменение себестоимости за счет изменения структуры
производства продукции:
Проверка:
Вывод к задаче
Средняя себестоимость изделия в отчетном периоде увеличилась на 2,8
руб., в том числе за счет изменения уровня себестоимости на 1,8 руб.,
увеличение доли продукции с более высокой себестоимостью увеличило
результативный показатель на 1 руб.
Для анализа уровня цен в практике ценообразования используются данные о средних ценах по однородным товарным группам.
При этом используются следующие показатели.
Простая средняя арифметическая цена:
где Цi – цена товара; Оi – объем товара.
Средняя арифметическая взвешенная цена:
где Ц – среднемесячная (среднеквартальная) цена единицы товара; О – объем проданных товаров в натуральных измерителях (тоннах, килограммах, литрах, метрах и др.).
Средняя хронологическая цена:
где Ц₁, Ц₂, Ц₃, … Цt – цены определенного периода (на начало или конец каждого месяца); t – число месяцев в определенном периоде.
Средняя хронологическая взвешенная цена:
где ЦСРi – средняя цена за конкретный период; ti – число месяцев в определенном периоде.
Средняя гармоническая взвешенная цена:
где Ц · О – товарооборот в рублях (цена единицы товара, умноженная на объем его продажи).
Индекс – это экономический и статистический показатель, характеризующий в относительном виде изменение экономических параметров во времени за определенный период и равный отношению конечной величины к исходной.
Индивидуальный индекс цен определяется по формуле:
где ЦО и ЦБ – цена товара соответственно отчетного (текущего) и базисного периодов.