Как найти динамику в экономике

Как рассчитать динамику показателей

Анализ динамики показателей начинается с того, как именно они изменяются (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за изменением рядов динамики во времени, рассчитываются показатели: абсолютное изменение, относительное изменение, темп изменения.

Инструкция

Учтите, что все данные показатели могут быть базисными, когда уровень одного периода сравнивается с уровнем начального периода, и цепными, когда сравнивается уровень двух соседних периодов.

Базисное абсолютное изменение (абсолютный прирост) вы можете рассчитать как разность конкретного и первого уровней ряда: У(б) = У(i ) – У(1). Оно показывает, насколько уровень конкретного периода больше или меньше базисного уровня. Цепное абсолютное изменение – это разность между конкретным и предыдущим уровнем ряда: У (ц) = У(i) – У(i-1). Оно показывает, на сколько единиц уровень конкретного периода больше или меньше предыдущего. Помните, что между базисным и цепным абсолютным изменением существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению.

При анализе динамики показателей вы можете рассчитать базисное относительное изменение (базисный темп роста). Он представляет собой отношение конкретного показателя к первому из ряда динамики: I(б) = У(i)/Y(1). Цепное относительное изменение – это соотношение конкретного и предыдущего уровня ряда: I(ц) = У(i)/Y(i-1). Относительное изменение показывает, во сколько раз уровень данного ряда больше уровня предыдущего ряда или какую часть его часть составляет. Относительное изменение может выражаться в процентах, путем умножения соотношения на 100 %. Между цепными и базисными относительными изменениями существует взаимосвязь: произведение цепных относительных изменений равно последнему базисному.

Кроме того, при анализе динамики показателей вы можете рассчитать темп изменения (темп прироста) уровней. Это относительный показатель, который показывает, на сколько процентов данный показатель больше или меньше другого, принимаемого за базу сравнения. Он определяется путем вычитания из относительного базисного или цепного изменения 100%: Т(i) = I(i) – 100%.

Источники:

• как найти абсолютное изменение
• Абсолютные и относительные статистические показатели
• Расчет абсолютных показателей

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Формулы для расчета показателей ряда динамики.

Подстрочные
символы “ц” и “б” отражают цепной и
базисный способы расчета показателей
ряда динамики.

Абсолютный
прирост
показывает, на сколько больше или меньше
значение уровня ряда с тем значением,
с которым проводится сравнение (соседним
или выбранным за базу сравнения).

или

(7.1)

Коэффициент
роста (темп роста) показывает,
во сколько раз больше или меньше значение
уровня ряда с тем значением, с которым
проводится сравнение (соседним или
выбранным за базу сравнения). Коэффициент
роста может быть выражен в процентах.

или

(7.2)

Темп
прироста характеризует
относительную скорость изменения уровня
ряда в единицу времени. Темп прироста
показывает, на какую долю (или процент)
уровень ряда рассматриваемого периода
больше или меньше базового (выбранного
для сравнения).

или
Т_ц,б=К_ц,б–1
или Т_ц,б=К_ц,б%–100%;
(7.3)

Предыдущий
показатель не отражает «вес» каждого
процента прироста. Например, в двух
бригадах урожайность зерновых выросла
по сравнению с предыдущим годом на 1,2%.
Но это не значит, что в натуральном
выражении это будет составлять одинаковое
количество центнеров. Оценить каждый
процент изменения позволяет следующий
показатель.

Абсолютное
значение 1% прироста
показывает натуральную величину
показателя, приходящегося на 1% изменения
относительно базисного (взятого за
основу сравнения) значения.

(7.4)

Формулы для расчета средних значений показателей ряда динамики:

1)
Средний уровень ряда может быть вычислен
по одной из формул (7.5 – для интервальных
радов; 7.6 – для моментных рядов)

или

(7.5)

(7.6)

2)
Средний абсолютный прирост:

или

(7.7)

где
(n
–1) – число периодов.

1. Средний
   темп роста:

,
(7.8)

где
n
– количество цепных темпов роста уровня
ряда

,
(7.9)

где
n
– число уровней ряда

4)
Средний темп прироста:

или

(7.10)

Средний
уровень ряда рассчитаем по формуле
средней арифметической простой У=1145,057

Средний
темп роста вычислим по любой из формул
8.8 или 8.9 и получим один и тот же результат
К= 0,9913= 99,13%. Это значение отражает среднее
ежегодное снижение численности населения
по сравнению с предыдущим периодом.

Средний темп
прироста (снижения) Т=-0,0087=–0,87%, т.е.
ежегодно на 0,87% уменьшалась численность
населения РБ.

Абсолютное среднее
ежегодное уменьшение численности
населения будут равно Δ =–9,97 тыс. чел.

Все
эти значения показывают ухудшающуюся
демографическую ситуацию в РБ.

Например:

Таблица
7.5. Численность сельского населения РБ
на начало года, тыс. чел.

Годы	Y	Δ	К	Т	А
ц	б	ц	б	ц	б	ц
1	1173,9	–	–	–	–	–	–	–
2	1166,2	-7,7	-7,7	0,993441	0,993441	-0,006559	-0,006559	1173,9
3	1156,5	-9,7	-17,4	0,991682	0,985178	-0,008318	-0,014822	1166,2
4	1146,1	-10,4	-27,8	0,991007	0,976318	-0,008993	-0,023682	1156,5
5	1135,1	-1,1	2309	0,990402	0,966948	-0,009598	-0,033052	1146,1
6	1123,5	-11,6	-50,4	0,989781	0,957066	-0,010219	-0,042934	1135,1
7	1114,1	-9,4	-59,8	0,991633	0,949059	-0,008367	-0,050941	1123,5

В
3. Приемы
выравнивания рядов динамики.

Часто
в рядах динамики сложно определить
общую тенденцию развития. Второй задачей
рядов динамики является выявление таких
периодов развития, которые достаточно
однородны по своим условиям и
взаимодействиям связей между показателями.

Под
тенденцией
понимается общее направление к росту,
снижению или стабилизации уровня явления
с течением времени.

Тенденция
по периодам может не совпадать с общей
тенденцией. Иногда вообще сложно
определить общую тенденцию. В этом
случае прибегают к различным методам
выравнивания ряда для определения его
тенденции:

1) способу укрупнения
интервалов;

2) сглаживанию ряда
с помощью скользящей средней;

3)
производят аналитическое выравнивание
и получают уравнение тренда.

Первый
способ
заключается в переходе от меньших
временных интервалов к большим и расчете
усредненных уровней ряда за укрупненный
интервал. Временной промежуток для
укрупнения интервала производят с
учетом общей длины анализируемого ряда
и величины исходных интервалов. Так,
например, если исходный ряд содержит
информацию за каждый месяц, то можно
перейти к укрупненному интервалу
величиной в квартал. Если представлена
информация по годам, то «укрупнение»
можно произвести за 2,3,4,5 лет в зависимости
от длины исходного ряда.

График
этого ряда изображен на рисунке 7.2, где
видно, что имеются периоды спада
производства продукции и периоды
подъема. Если рассмотреть только часть
графика, начиная с 1998 года по 2005, то
сложно установить общую тенденцию
производства продукции данного вида.
Поэтому более четко общая тенденция
будет просматриваться, если произвести
выравнивание ряда одним из методов.
Так, использование метода укрупнения
интервалов дает результаты, представленные
в таблице 7.6 и 7.7.

Например:

Таблица
7.6. Производство цельномолочной продукции
в пересчете на молоко, тыс. тонн.

Годы	Цельномолочная продукция в пересчете на молоко	Годы	Цельномолочная продукция в пересчете на молоко
1995	801	2001	963
1996	744	2002	906
1997	813	2003	927
1998	952	2004	992
1999	1032	2005	1122
2000	954	2006	1284

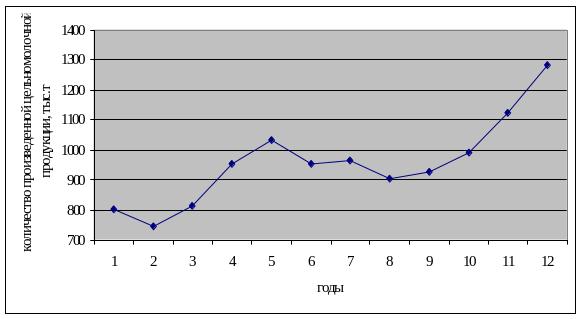
Рисунок
7.2. График динамики производства
цельномолочной продукции в РБ

Таблица
7.7. Расчет производства цельномолочной
продукции по укрупненным периодам
(трехлетиям).

Укрупненные периоды	Сумма цельномолочной продукции в пересчете на молоко	Среднегодовое производство цельномолочной продукции в пересчете на молоко
1995-1997	2358	786,0
1998-2000	2938	979,3
2001-2003	2796	932,0
2004-2006	3398	1132,7

Алгоритм
расчета:

801+744+813
= 2358; 2358/3=786,0

952+1032+954=2938;
2938/3=979,3 и т.д.

Из
последнего столбика таблицы 7.7 и рисунка
7.3 более четко видна тенденция к росту
производства цельномолочной продукции.

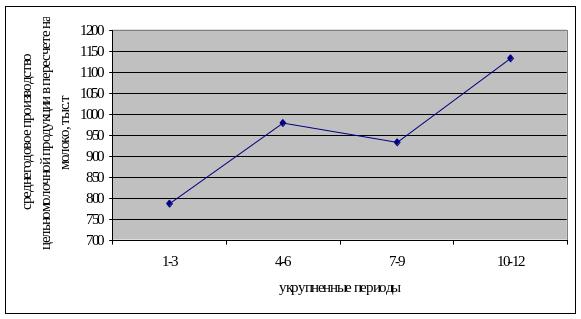
Рисунок
7.3. График ряда, выровненного по укрупненным
интервалам

Второй
способ
заключается в последовательном расчете
средних уровней за выбранный лаг времени,
передвигая этот лаг

на
1 интервал по времени t.
Величину лага L
выбирают произвольно в зависимости от
длины анализируемого ряда: L
= 2, 3, 4, …, n
. Например, мы выберем трехлетний лаг.
И тогда выровненный ряд можно представить
в следующей таблице (7.8).

Алгоритм расчета:

801+744+813=2358; 2358/3=786,0

744+813+952=2509; 2509/3=836,3

813+952+1032=2797;
2797/3=932,3 и т.д.

В настоящее время
в основном используют третий метод,
который рассмотрим в следующем вопросе.

Таблица
7.8 – Расчет трехлетней скользящей
средней.

Годы	Цельномолочная продукция в пересчете на молоко, тыс. т	Сумма цельномолочной продукции в пересчете на молоко по трехлетиям, тыс. т	Трехлетняя скользящая средняя, тыс. т
1995	801	–	–
1996	744	–	–
1997	813	2358	786,0
1998	952	2509	836,3
1999	1032	2797	932,3
2000	954	2938	979,3
2001	963	2949	983,0
2002	906	2823	941,0
2003	927	2796	932,0
2004	992	2825	941,7
2005	1122	3041	1013,7
2006	1284	3398	1132,7

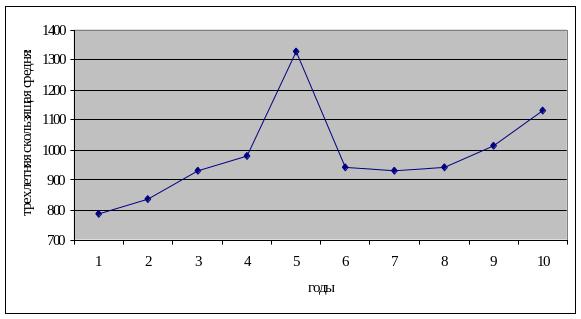
Рисунок
7.4. График ряда, выровненного по скользящей
средней

В
4. Тренд.
Аналитическое выравнивание ряда.
Прогнозы по тренду.

Самые
точные результаты выравнивания ряда
динамики дает аналитическое выравнивание,
с помощью которого строят математическое
уравнение, наилучшим образом описывающее
тенденцию изменения показателя.

Понятие
об уравнении тенденции динамики ввел
в 1902 году английский ученый Р.Гукер. Он
предложил называть такое уравнение
трендом (the
trend).

Под
трендом
понимают уравнение линии во времени,
вдоль которой расположена ломаная ряда
динамики.

Этапы построения
тренда:

1.
Выявляют этапы развития явления (спады,
подъемы, однородные участки и т.д.).

2.
Анализируют показатели ряда динамики
на этих этапах и выбирают вид уравнения
(вид тренда).

3.
Вычисляют параметры тренда, используя
метод наименьших квадратов.

4.
Оценивают адекватность уравнения
развитию анализируемого показателя,
оценивая колеблемость фактических
уровней ряда вокруг теоретических, т.е.
вычисленных по тренду.

Рассмотрим
3-ий этап на простейшем примере, когда
трендом является уравнение прямой
линии. Будем искать уравнение в виде:

(7.11)

где
t
– параметр времени; Y_t
– соответствующие времени уровни ряда,
Ŷ_t–
выровненные уровни ряда, т.е. вычисленные
по тренду.

Исходную
информацию и расчетные показатели
представим в виде таблицы 7.9.

Используя
метод наименьших квадратов, построим
систему уравнений:

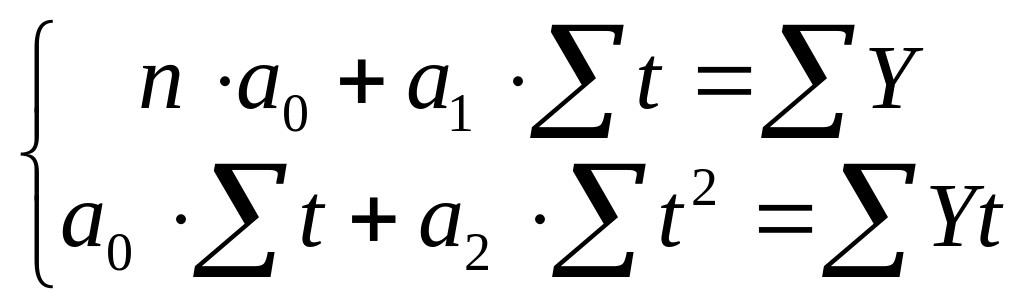
(7.12)

Таблица
7.9. Схема таблицы для расчета параметров
тренда

t	Yi	t2	Y∙t	Ŷ
1 2 3 … n	Y1 Y2 Y3 … Yn			Ŷ Ŷ
t	Y	t2	(Y∙t)	ΣŶ

Решение
этой системы позволит найти значения
параметров уравнения. Если уравнение
построено качественно, то Y_i
= Σ Ŷ_t
.

Эти
расчеты можно упростить, если иначе
производить номерацию параметра t.
Ее нужно произвести следующим образом:
начало отсчета должно находиться в
середине анализируемого ряда. Если
количество точек нечетное, то в середине
ряда t
ставим 0; если количество точек четное,
то нуль выбрасывается. К началу ряда
счет идет со знаком «–», к концу – со
знаком «+», тогда t
становиться равной 0 (т.е. t=0).

Таблица
7.10. Схема номерации уровней ряда от
середины ряда

t для нечетного количества уровней ряда	t для четного количества уровней ряда
–к	–к
…	…
–2	…
–1	–2
0	–1
+1	+1
+2	+2
…	…
+к	+к
кi=0	кi=0

Тогда
в системе нормальных уравнений (7.12)
исчезнут слагаемые, в которые входит
сумма t
(Σt=0),
т.е. мы получим упрощенную систему

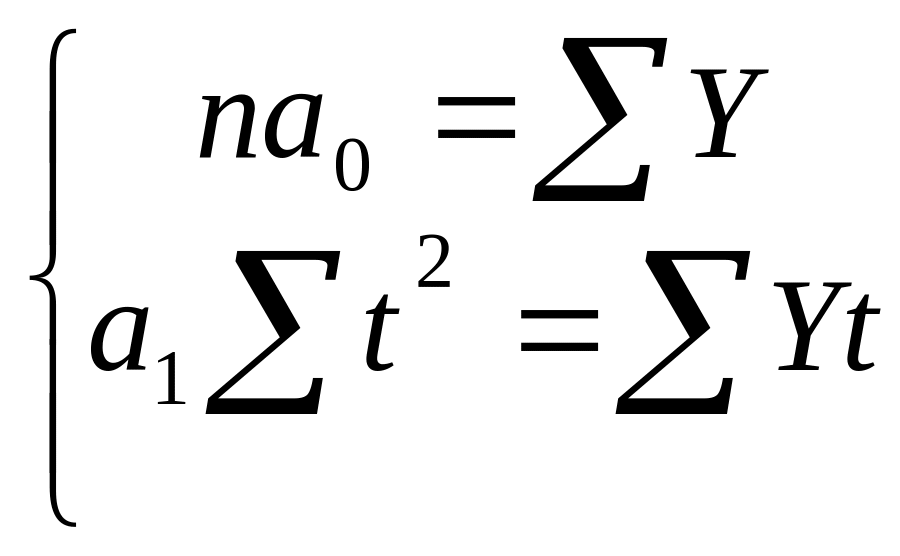
(7.13)

где
n
– количество точек анализируемого
ряда.

Отсюда:

(7.14)

(7.15)

Параметр
а₁
соответствует абсолютному приросту за
единицу периода времени.

Тенденции
или тренды могут быть выражены в виде
кривых. Это могут быть: парабола, ветка
гиперболы, экспонента или показательная
кривая, логарифмическая линия и т.д.
Виды трендов в виде кривых и их построение
рассмотрим ниже.

Прогноз
по тренду.
Используя уравнение можно построить
точечный прогноз на последующие периоды
времени, подставляя в уравнение тренда
(7.11) номера t,
следующие за последним фактическим
номером, используемым при построении
тренда. Например:

Таблица
7.11. Схема расчета прогноза при различной
номерации показателей ряда динамики

Номерация t от начала ряда	Номерация t от середины ряда
1	-6
2	…
…	-1
11	+1
прогноз 12	+2
прогноз 13	…
прогноз 14	+6
прогноз 15	прогноз 7
и т.д.	прогноз 8

Параметры
а₀
и а₁
в уравнении тренда, построенных различным
способом нумерации t, будут отличаться,
а прогнозы будут совпадать.

Оценка
точности тренда.
В экономическом анализе необходимо
оценить силу разброса фактических точек
вокруг расчетных (трендовых). Это
оценивается по величине остаточного
среднеквадратического отклонения и
коэффициенту вариации:

(7.16)

где
n
– число уровней ряда; m
– число параметров в уравнении тренда
(например, для прямой m=2,
для параболы m=3).

(7.17)

г
де
Y_i
– средний
уровень ряда.

Чем
меньше значения σ_ост.
и V,
тем лучше тренд отражает тенденцию
изменения показателя.

Имея оценку качества
тренда, производят оценку качества
прогноза на перспективу.

Для
точечного прогноза по тренду, также как
и для выборочного наблюдения, необходимо
оценить среднюю ошибку прогноза.

Для
линейного тренда средняя ошибка прогноза
рассчитывается:

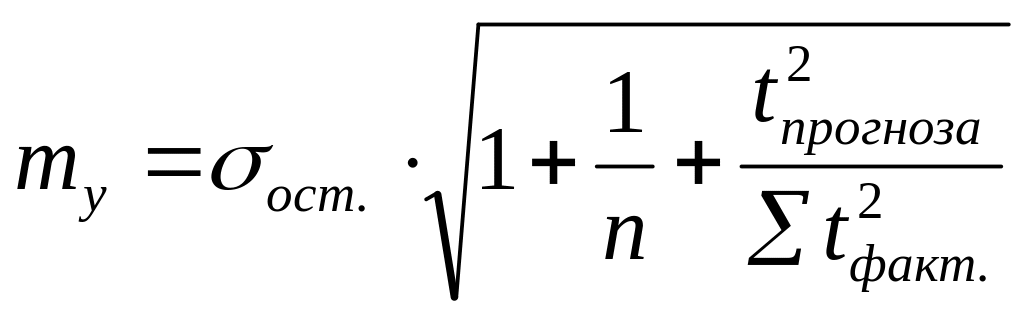
(7.18)

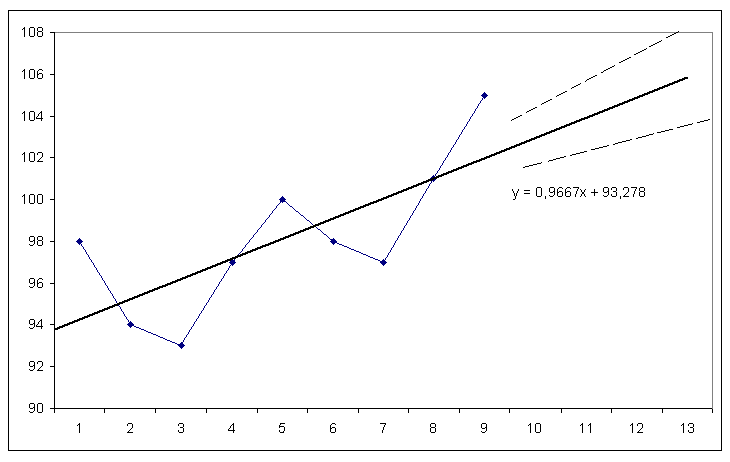
Рисунок
7.5. Точечное и интервальное прогнозирование

Доверительный
интервал или предельная ошибка прогноза
равна средней ошибке умноженной на
коэффициент доверия t-Стьюдента,
при доверительных вероятностях p=0,90;
0,95; 0,99. Строчку в таблицах находим по
числу степеней свободы тренда n
– m
.

В
5. Сезонные колебания в рядах динамики

Если
ряд динамики насчитывает достаточное
количество уровней, например 100, то можно
обнаружить колебания, которые повторяются,
т.е. наличие регулярных спадов и подъёмов.
Такие макроэкономические колебания
называются циклическими.
Такого вида колебания рассматриваются
в курсе макроэкономики, когда оценивают
динамику экономического развития
отдельных государств.

Внутри
годичные колебания, имеющие регулярный
характер, т.е. повторяющиеся из года в
год, называются сезонными
.

Сезонные
подъёмы и спады в производстве снижают
равномерность, устойчивость технологического
процесса и реализации продукции и должны
учитываться при планировании производства.

Сезонные
колебания показателя могут накладываться
на тенденцию роста или спада фактора,
а могут наблюдаться при постоянной
случайной колеблемости. В зависимости
от этого графики могут иметь следующий
вид:

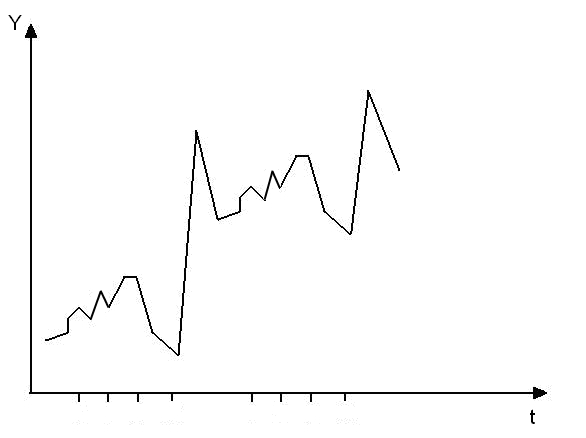
Рисунок
7.6. Наличие тенденции, случайных и
сезонных колебаний

На
рисунке хорошо видны спады в четвертом
квартале и подъемы в первом. В остальные
периоды наблюдается случайная колеблемость
при наличии тенденции к росту показателя.

На
рисунке 7.7. видно, что изменение показателя
не имеет тенденции ни к росту, ни к
снижению. Однако видна четко выраженная
сезонная колеблемость показателя, т.е.
есть периоды «впадин» и «подъемов».

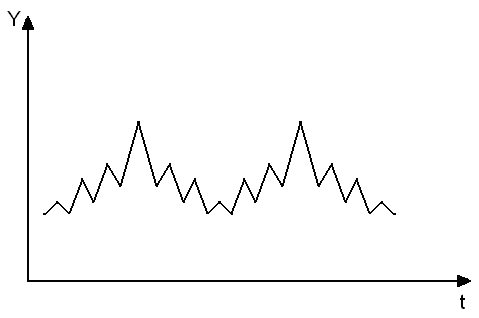
Рисунок
7.7. Наличие сезонных и случайных колебаний

Чаще
всего степень сезонных колебаний
определяют по величине индекса сезонности.
Различают индивидуальные индексы
сезонности и средние, с учётом тренда
и без его наличия.

Если
тренд отсутствует, то индивидуальный
индекс сезонности может быть вычислен
как отношение величины месячного
(квартального) уровня к среднегодовому:

(7.19)

Средний
индекс сезонности равен сумме
индивидуальных индексов сезонности,
делённой на количество сезонов n.
Так как анализ может проводиться за
несколько полных лет и один (последний)
неполный год, то число n
будет различным для той части времени,
где учитываются только полные годы и
для той, где есть дополнительно значения
ряда за неполный год.

(7.20)

В
сельском хозяйстве анализ сезонных
колебаний на основе данных поквартального
учёта несколько ухудшает показатель
сезонности, потому что времена года
(сезоны) не совпадают с календарными
периодами. Поэтому исследование наличия
сенных колебаний лучше
проводить на основании данных помесячного
учета.

Если
анализируемый показатель имеет не
только сезонные колебания, но и достоверную
тенденцию (тренд), то в знаменателе
берётся показатель ряда, взятый по
тренду:

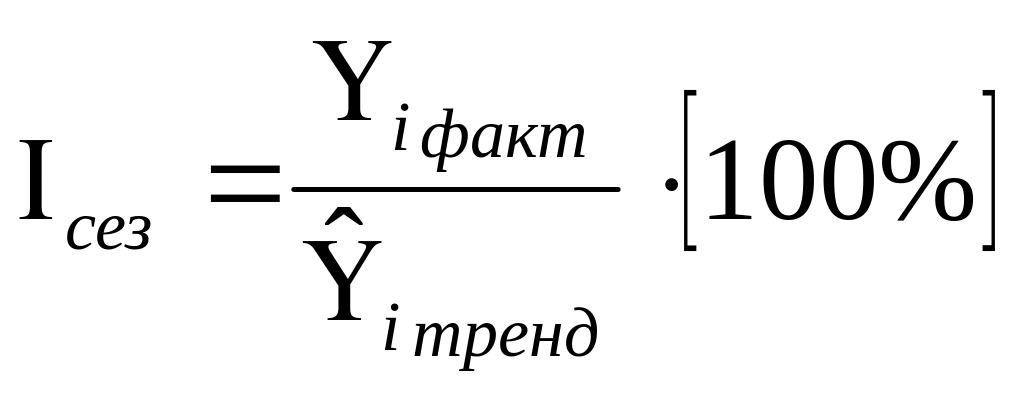
(7.21)

Оценка
индекса сезонности осуществляется по
среднему линейному или среднеквадратическому
отклонению для каждого года. Если
коэффициенты сезонности (линейный и
среднеквадратический) увеличиваются,
то это свидетельствует об усилении
сезонных колебаний; если уменьшаются,
то наоборот.

Среднее
линейное отклонение коэффициента
сезонности рассчитывают по формуле:

=

(7.22)

Среднеквадратическое
отклонение коэффициента сезонности
рассчитывают по формуле:

=

(7.23)

где
n – число сезонов.

Чем
меньше значения этих показателей, тем
меньше сезонная колеблемость и выше
стабильность показателя.

В
6. Модели рядов с учетом тенденции и
сезонности.

Тенденцию
ряда и наличие сезонности можно
представить в виде двух различных
моделей:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание курса лекций «Статистика»

Статистическое изучение динамики социально-экономических явлений

Процессы и явления социально-экономической жизни общества, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Для того, чтобы выявить тенденции и закономерности социально-экономического развития явлений, статистика строит особые ряды статистических показателей, которые называются рядами динамики (иногда их называют временными рядами), то есть ‑ это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В англоязычной литературе для временных рядов используется термин «time series». Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.

Каждый ряд динамики характеризуется двумя параметрами: значениями времени и соответствующими им значениями уровней ряда. Уровни ряда обычно обозначаются «y_t»: y₁, y₂ и т.д. В качестве показателя времени в рядах динамики могут указываться отдельные периоды (сутки, месяцы, кварталы, годы и т.д.) времени или определенные моменты (даты). Время в рядах динамики обозначается через «t».

Ряд динамики состоит из двух элементов:

1) уровня ряда (значения изучаемого показателя);

2) моментов (периодов) времени, когда фиксируется этот показатель.

Основные способы обработки рядов динамики:

1) укрупнение интервалов и расчет для них средних показателей;

2) сглаживание уровней способом скользящей средней;

3) выравнивание по аналитическим формулам.

Суть последнего способа заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени.

Ряды динамики, как правило, представляют в виде таблицы или графически.

Ряды динамики могут быть классифицированы по следующим признакам:

В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин ‑ как производные.

Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.

Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производ­ства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.

Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.

В зависимости от характера временного параметра ряды динамики делятся на моментные и интервальные.

Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени.

Пример. Моментный ряд динамики, характеризующий численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г., представлен в таблице 13.1.

Таблица 13.1 ‑ Численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г

Дата	1.01	1.02	1.03	1.04	1.05	1.06
Численность персонала, чел.	780	810	880	930	940	970

Следует помнить, что моментные ряды абсолютных величин нельзя суммировать. Бессмысленно, например, складывать численность персонала по состоянию на 1 января, 1 февраля и т.д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же единицы совокупности.

---

Ряд, в котором уровни характеризуют результат, накопленный или вновь произве­денный за определенный интервал времени, называется интервальным.

Пример. Интервальный ряд динамики, представлен в таблице 13.2.

Таблица 13.2. ‑ Характеристика динамики объема розничного товарооборота

Дата	2004	2005	2006	2007	2008
Товарооборот, млн. руб.	28,3	31,9	38,3	42,3	45,2

Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда вполне реальный показатель, например, общий объем розничного товарооборота за 2004-2008 г.г.

---

В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и не равноотстоящими уровнями во времени.

Ряды динамики следующих друг за другом периодов или следующих через оп­ределенные промежутки дат называются равноотстоящими, пример (табл. 13.1 и табл. 13.2).

Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими, пример(табл. 13.3).

Пример. Рядом динамики с не равноотстоящими уровнями во времени может служить объем экспорта продукции предприятия, представленный в таблице 13.3.

Таблица 13.3. – Динамика объема экспорта продукции предприятия

Годы	1993	1996	1998	2000	2004
Объем экспорта, млн. долл.	1110	1220	1320	1450	1640

---

По числу показателей можно выделить изолированные (одномерные) и  комплексные (многомерные) ряды динамики.

Если ведется анализ во времени одного показателя ряда, то ряд динамики изолированный (например, данные о производст­ве газа по годам). В многомерном ряду представлена динамика нескольких показателей, характеризующих одно явление.

---

Сопоставимость уровней и смыкание рядов динамики

Важнейшим условием правильного построения рядов динамики является сопоста­вимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.

---

Рассмотрим основные причины несопоставимости уровней ряда динамики.

Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета.

Пример. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие ‑ в квадратных метрах.

---

На сопоставимость уровней ряда динамики непосредственно влияет методоло­гия учета или расчета показателей.

Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие ‑ с убранной, то такие уровни будут не­сопоставимы.

---

В процессе развития во времени, прежде всего, происходят количественные измерения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.

---

Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл.

Например, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.

---

Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных  границ областей, районов и так далее.

---

Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).

Пример. Предположим, что в N-ом регионе имеются данные об общем объеме оборота розничной торговли за 2013-2015 гг. в фактически действующих ценах, и за 2015-2018 гг. ‑ в сопоставимых ценах (табл. 13.4.).

Таблица 13.4 ‑ Динамика общего объема оборота розничной торговли (млрд. руб.) цифры условные

Годы	2013	2014	2015	2016	2017	2018
Оборот розничной торговли, млрд. руб. (в фактически действующих ценах)	19,7	20	21,2
Оборот розничной торговли, млрд. руб. (в сопоставимых ценах)			22,8	24,6	25,2	26,1
Сомкнутый ряд абсолютных величин (в сопоставимых ценах; млрд. руб.)	21,3	21,5	22,8	24,6	25,2	26,1
Сопоставимый ряд относительных величин (в % к 2005 г.)	92,9	94,3	100	107,9	110,5	114,5

Решение. Чтобы проанализировать динамику общего объема розничной торговли за 2013-2018 гг., необходимо сомкнуть (объединить) приведенные выше два ряда в один. А чтобы уровни нового ряда были сопоставимы, необходимо пересчитать данные 2003-2005 гг. в сопоставимые цены. Для этого на основе данных об объеме розничной торговли за 2005 г. в фактических и сопоставимых ценах находим соотношение между ними: 22,8:21,2 = 1,08. Умножая на полученный коэффициент данные за 2003-2005 гг., приводим их, таким образом, к сопоставимому виду с последующими уровнями. Сомкнутый (сопоставимый) ряд динамики показан в предпоследней строке таблицы 13.4.

---

Другой способ смыкания рядов заключается в том, что уровни года, в котором произошли изменения (в нашем примере ‑ уровни 2005 г.), как до изменений, так и после изменений (для нашего примера ‑ в фактических и сопоставимых ценах, т.е. 21,2 и 22,8) принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно (в нашем примере в фактических ценах ‑ по отношению к 21,2, в сопоставимых ценах ‑ к 22,8). В результате получаем сомкнутый ряд динамики, который показан в последней строке таблицы 13.4.

---

Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, администра­тивных и территориальных районов. Это, во-первых, вопрос о сопоставимости цен срав­ниваемых стран, во-вторых, вопрос о сопоставимости методики расчета сравниваемых показателей. В таких случаях ряды динамики приводятся к одному основанию, то есть к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.

---

---

Аналитические показатели ряда динамики

На практике для количественной оценки динамики явлений широко применяется ряд основных аналитических показателей. К таким показателям относятся, абсолютный прирост при этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.

---

Абсолютный прирост (∆y ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста.

∆y – абсолютный прирост – это разность между уровнями ряда динамики. Может быть цепным или базисным:

---

---

Показатель интенсивности изменения уровня ряда ‑ в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста.

Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).

---

Тр– темп роста – относительный показатель, получающийся в результате сопоставления двух уровней одного ряда динамики. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:

---

либо как базисные, когда все уровни сопоставляются с одним и тем же уровнем, выбранным за базу сравнения (при умножении на 100 – в процентном выражении):

---

Между цепными и базисными темпами роста существует взаимосвязь: произведение всех цепных темпов роста равно последнему базисному.

---

 Т пр – темп прироста – относительный показатель, показывающий, насколько один уровень ряда динамики больше или меньше другого, принимаемого за базу сравнения:

---

При делении абсолютного прироста (цепного) на темп прироста (цепной) получим показатель, называемый значением одного процента прироста – А:

---

Пример. Произведем расчет и анализ динамики заключения браков в Омской области за 2000–2003 гг., используя формулы вышеизложенных показателей и данные табл. 13.5.  За базу сравнения примем уровень 2000 года.

Таблица 13.5 – Показатели изменения уровней ряда динамики

Показатели	Год
2000	2001	2002	2003
Заключение браков, единиц	13277	15130	15880	16458

Абсолютные приросты,  ∆y

Далее в табл. 13.6 приведем всю совокупность показателей ряда динамики, позволяющую посмотреть взаимосвязи между ними.

Таблица 13.6 – Показатели изменения уровней ряда динамики

Показатели	Год
2000	2001	2002	2003
1. Заключение браков, единиц	13277	15130	15880	16458
2. Темпы роста базисные:	−	1,14	1,196	1,24
2.1. коэффициенты
2.2. проценты	−	114	119,6	124
3. Темпы роста цепные:	−	1,14	1,05	1,036
3.1. коэффициенты
3.2. проценты	−	114	105	103,6
4. Абсолютные приросты, ед.	−	1853	2603	3181
4.1. базисные (2000 г.)
4.2. цепные (по годам)	−	1853	750	578
5. Темпы прироста базисные	−	0,14	0,196	0,24
5.1. коэффициенты
5.2. проценты	−	14	19,6	24
6. Темпы прироста цепные	−	0,14	0,05	0,036
6.1. коэффициенты
6.2. проценты	−	14	5	3,6
7. Абсолютное значение 1 % пр.	−	132,36	150	160,6

При изучении ряда динамики важно проследить за направлением и размером изменений уровня ряда во времени. С этой целью для динамических рядов рассчитываются следующие показатели.

Среднегодовой темп роста, ориентированный на достижение конечного уровня (y_n) в исследуемом периоде, можно рассчитать как среднюю геометрическую из годовых темпов роста по следующим формулам:

(13.7)

Если же ориентация берется на достижение суммарного значения (объема) исследуемого показателя за определенный период, то для расчета среднего коэффициента (темпа) роста используется так называемая средняя параболическая вида

(13.8)

где значение k определяется по специальной таблице для расчета средних коэффициентов роста (снижения) по средней параболической.

Пример. Таблица 13.7 – Данные о вводе в действие жилой площади в городе N

Год	2002	2003-2008
Введено млн. кв. м общей площади, уi	62,5	394,7

Определим среднегодовой темп роста ввода в действие жилой площади за 2003‑2008 гг. (т.е. за 6 лет), ориентированный на достижение общей суммы введенного жилья за указанный период (т.е. 394, 7 млн. кв.м).

Решение. Используем формулу (13.8) средней параболической:

далее по таблице для расчета средних коэффициентов роста (снижения) по средней параболической в графе n=6 находим значение, наиболее близкое к полученному отношению (6,315). Это число 6,323, которому соответствует =1,015. Это искомый среднегодовой коэффициент роста ввода жилья за 6 лет. Отсюда, среднегодовой темп роста ввода в действие жилой площади за указанный период составлял 101,5%, а среднегодовой темп прироста был равен 101,5% ‑ 100% =1,5%.

Пример. Таблица 13.8 – Данные о прибыли на предприятии за 2000‑2005 гг.

Год	2000	2001	2002	2003	2004	2005
Валовая прибыль, млн руб.	566	521	447	428	391	367

Рассчитаем среднегодовой темп роста(снижения) за 2000‑2005 гг., ориентированный:

• достижение фактического уровня в 2005 г. по формуле (13.7)

или 91,7%, т.е. ежегодно объем прибыли уменьшался в среднем на 8,3%;

• если при расчете ориентироваться на общий объем, за 5 лет, то применим для расчета формулу (13.8):

Пример. Имеются данные о численности мужской части населения Омской области за 5 лет на начало года (табл. 10.11):

далее по таблице =0,91, т.е. среднегодовое снижение прибыли при общем объеме за 5 лет составило 9%.

На практике, т.к конечный уровень ряда может быть случайным(нехарактерным), чаще применяется расчет по формуле (13.8), где учитывается сумма уровней за n лет.

Прогнозирование на основе рядов динамики

Суть нижеприведенного способа (выравнивание по аналитическим формулам) заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени, т.е.

Таблица 13.9 – Численность мужской части населения в 1999–2003 гг. (на 1.01.),

Год	1999	2000	2001	2002	2003
Численность тыс. чел.	1028,8	1020,1	1010,7	999,6	989,8

Найдем линию тренда и, используя полученное уравнение, сделаем прогноз на будущее (определим численность мужской части населения в Омской области в 2006 году).

Предположим, что численность населения изменяется во времени по прямой:

(13.9)

Для нахождения параметров а₀ и а₁ решим систему нормальных уравнений, отвечающих требованию способа наименьших квадратов

(13.10)

Далее в табл. 10.12 рассчитаны необходимые для решения системы уравнения суммы: ∑, ∑t, ∑t², ∑yt. Годы последовательно обозначим как 1, 2, 3, 4, 5 (n=5).

Таблица 13.10 – Расчетные данные для определения параметров уравнения тренда

Год	Число мужчин, тыс. чел. yi	Условное обозначение времени, t	t2	y·t	Уравнение тренда
1999	1028,8	1	1	1028,8	1029,5
2000	1020,1	2	4	2040,2	1019,65
2001	1010,7	3	9	3032,1	1009,8
2002	999,6	4	16	3998,4	999,95
2003	989,8	5	25	4949	990,1
∑	5049	15	55	15048,5	5049

Из системы уравнений получим a₁ = −9,85; а₀ = 1039,35;

Отсюда искомое уравнение тренда

Для 2006 года t = 8; следовательно,  То есть по прогнозу численность мужской части населения в Омской области в 2006 году составит 960,55 тыс. чел.

Для решения данной задачи можно использовать и второй способ, упрощенный. Если время t обозначить так, чтобы ∑t = 0, т.е. счет вести от середины ряда, то система упростится и примет вид

(13.11)

В этом случае каждое уравнение решается самостоятельно:

(13.12)

(13.13)

Необходимые для расчета параметров уравнения суммы приведем в табл. 10.13.

Таблица 13.11 – Расчетные данные для определения параметров уравнения тренда

Год	Число мужчин, тыс. чел. yi	Условное обозначение времени, t	t2	yt	Уравнение тренда
1999	1028,8	-2	4	-2058	1029,5
2000	1020,1	-1	1	-1020	1019,65
2001	1010,7	0	0	0	1009,8
2002	999,6	1	1	999,6	999,95
2003	989,8	2	4	1979,6	990,1
Итого	5049	0	10	-98,5	5049

Тогда  и

Уравнение тренда в этом случае будет имеет вид

Для 2006 г. t = 5; следовательно,

Эта величина условная, рассчитанная при предположении, что линейная закономерность изменения численности мужской части населения, принятая для 1999–2003 гг., сохранится на последующий период до 2006 г.

Контрольные задания.

По данным статистических ежегодных изданий: «Российский статистический ежегодник», «Россия в цифрах» и т.п. выберите несколько показателей, постройте и проанализируйте ряды динамики, найдите линию тренда и, используя полученное уравнение, сделайте прогноз на 3 года вперед.

АНОНС…полный текст будет опубликован позднее… в соответствии с графиком занятий

Содержание курса лекций «Статистика»

Показатели динамики: темп роста и темп прироста

Темп роста

Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.

Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста

Коэффициент роста может быть рассчитан по формулам:

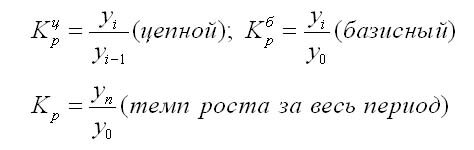
Также темп роста может определяться так:

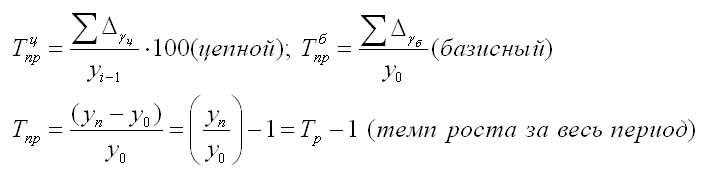
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.

Абсолютный прирост

Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:

1. Абсолютный прирост (цепной):

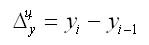
2. Абсолютный прирост (базисный):

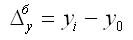
где уi — уровень сравниваемого периода;

Уi-1 — Уровень предшествующего периода;

У0 — уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:

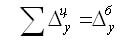
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.

Темп прироста

Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:

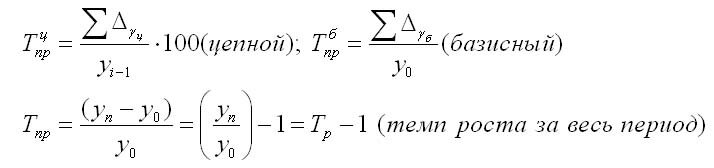
Темп прироста можно получить из темпа роста:

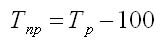
Коэффициент прироста может быть получен таким образом:

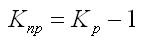
Абсолютное значение 1%-го прироста

Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:

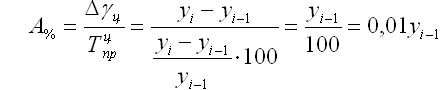
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.

Примеры расчетов показателей динамики

Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики

Пример 1. Расчет среднемесячного темп роста объема продаж

Пример 2. Определение всех показателей динамики (подробный расчет)

Пример 3. Расчет цепных, базисных и средних показателей динамики

О показателях динамики

При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.

Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.

Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

Понятие и состав основных экономических показателей деятельности предприятия

Экономические показатели способствуют отражению состояния экономики в целом и отдельных ее объектов. Они являются самым распространенным инструментарием описания экономических процессов.

По своей структуре экономические показатели бывают абсолютные, относительные и объемные.

Абсолютные и объемные показатели выражаются в денежных и натуральных единицах, а относительные – в процентах, либо как коэффициент.

К основным показателям деятельности субъекта хозяйствования можно отнести следующие:

1. Рентабельность продаж
2. Рентабельность капитала
3. Рентабельность деятельности
4. Фондоотдача
5. Фондовооруженность
6. Фондорентабельность

Стоит отметить, что данный перечень показателей неполный, поскольку для полного экономического анализа требуется расчет иных показателей рентабельности, ликвидности и деловой активности, а также рекомендуется провести вертикальный и горизонтальный анализ бухгалтерской (финансовой) отчетности.

Порядок расчета основных экономических показателей деятельности предприятия

Основные экономические показатели деятельности хозяйствующего субъекта рассчитываются исходя из показателей финансовой отчетности. Главенствующую роль в расчетах показателей играют показатели прибыли:

• Рентабельность продаж рассчитывается путем деления прибыли от продаж на выручку.
• Рентабельность капитала равна частному от деления чистой прибыли на стоимость капитала субъекта хозяйствования.
• Рентабельность деятельности – отношение балансовой прибыли (прибыли до налогообложения) к средней величине активов.
• Фондоотдача равняется отношению выручки к стоимости основных производственных фондов.
• Фондовооруженность – отношение стоимости ОПФ к численности персонала субъекта хозяйствования.
• Фондорентабельность – отношение балансовой прибыли к среднегодовой стоимости ОПФ.

«Расчет и динамика основных экономических показателей» 👇

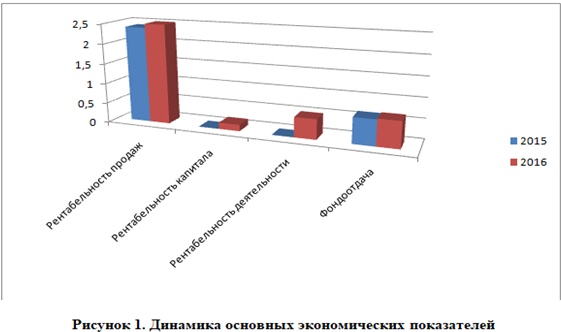
Динамика основных экономических показателей деятельности предприятия

Как говорилось выше, для определения эффективности деятельности любого хозяйствующего субъекта, необходимо провести анализ экономических показателей.Их динамика говорит об увеличении, либо снижении эффективности деятельности субъекта хозяйствования.

Если рассматривать динамику показателей основных экономических показателей условного предприятия, то видно, что показатели рентабельности возрастают ввиду роста чистой прибыли. Показатели фондоотдачи и фондовооруженности также увеличились.

Для наглядности можно изобразить динамику основных экономических показателей графически.

Как видно, рисунок способствует наглядной оценке динамики основных экономических показателей.