Как найти диоганаль квадрата

Как найти диоганаль квадрата


Загрузить PDF


Загрузить PDF

Диагональ квадрата — это отрезок, который соединяет противолежащие углы квадрата и проходит через его центр. Чтобы вычислить диагональ квадрата, воспользуйтесь формулой d=s{sqrt {2}}, где s — сторона квадрата. В задачах требуется найти диагональ квадрата по данному значению другой величины, например, периметра или площади. В этих случаях необходимо использовать другие формулы, чтобы сначала вычислить сторону квадрата, а потом – его диагональ.

  1. Изображение с названием Calculate a Diagonal of a Square Step 1

    1

    Найдите длину стороны квадрата. Скорее всего, значение длины стороны квадрата будет дано в условии задачи. Если же вы работаете с реальным предметом, измерьте его сторону при помощи линейки или рулетки. Так как у квадрата все стороны равны, измерьте или найдите длину любой стороны. Если длина стороны квадрата неизвестна, этим методом пользоваться нельзя.

    • Например, дан квадрат со стороной 5 см.

  2. Изображение с названием Calculate a Diagonal of a Square Step 2

    2

  3. Изображение с названием Calculate a Diagonal of a Square Step 3

    3

    Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо s.

    • Например, если сторона квадрата равна 5 см, формула запишется так:
      d=5{sqrt {2}}

  4. Изображение с названием Calculate a Diagonal of a Square Step 4

    4

    Умножьте сторону квадрата на {sqrt {2}}, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите {sqrt {2}} до 1,414.

    Реклама

  1. Изображение с названием Calculate a Diagonal of a Square Step 5

    1

  2. Изображение с названием Calculate a Diagonal of a Square Step 6

    2

    Подставьте в формулу значение периметра квадрата. То есть данное значение нужно подставить вместо P.

    • Например, периметр квадрата равен 20 см. Запишите формулу так:
      20=4s

  3. Изображение с названием Calculate a Diagonal of a Square Step 7

    3

    Найдите s. Для этого разделите каждую сторону уравнения на 4. В результате будет вычислена сторона квадрата.

  4. Изображение с названием Calculate a Diagonal of a Square Step 8

    4

  5. Изображение с названием Calculate a Diagonal of a Square Step 9

    5

    Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо s.

    • Например, если сторона квадрата равна 5 см, формула запишется так:
      d=5{sqrt {2}}

  6. Изображение с названием Calculate a Diagonal of a Square Step 10

    6

    Умножьте сторону квадрата на {sqrt {2}}, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите {sqrt {2}} до 1,414.

    Реклама

  1. Изображение с названием Calculate a Diagonal of a Square Step 11

    1

  2. Изображение с названием Calculate a Diagonal of a Square Step 12

    2

    В формулу подставьте значение площади квадрата. То есть данное значение нужно подставить вместо A.

    • Например, площадь квадрата равна 25 см2. Запишите формулу так:
      25=s^{{2}}.

  3. Изображение с названием Calculate a Diagonal of a Square Step 13

    3

    Найдите s. Для этого извлеките квадратный корень из значения площади квадрата. В результате будет вычислена сторона квадрата. Воспользуйтесь калькулятором, чтобы извлечь квадратный корень. Если квадратный корень нужно извлечь вручную, прочитайте эту статью.

  4. Изображение с названием Calculate a Diagonal of a Square Step 14

    4

  5. Изображение с названием Calculate a Diagonal of a Square Step 15

    5

    Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо s.

    • Например, если сторона квадрата равна 5 см, формула запишется так:
      d=5{sqrt {2}}

  6. Изображение с названием Calculate a Diagonal of a Square Step 16

    6

    Умножьте сторону квадрата на {sqrt {2}}, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите {sqrt {2}} до 1,414.

    Реклама

Что вам понадобится

  • Калькулятор

Об этой статье

Эту страницу просматривали 424 398 раз.

Была ли эта статья полезной?

Источник


Download Article


Download Article

The diagonal of a square is the line stretching from one corner of the square to the opposite corner. To find the diagonal of a square, you can use the formula d=s{sqrt {2}}, where s equals one side length of the square. Sometimes, however, you might be asked to find the length of the diagonal given another value, such as the perimeter or area of the square. In these instances it is necessary to use different formulas first, so that you can determine the side length before using the diagonal formula.

  1. Image titled Calculate a Diagonal of a Square Step 1

    1

    Find the length of one side of the square. This will probably be given to you. If you are working with a square in the real world, use a ruler or piece of measuring tape to find the length. Since all four sides of the square are the same length, you can use any side of the square. If you do not know the length of one side of the square, you cannot use this method.

    • For example, you might want to find the length of the diagonal of a square that has sides 5 centimeters long.

  2. Image titled Calculate a Diagonal of a Square Step 2

    2

    Advertisement

  3. Image titled Calculate a Diagonal of a Square Step 3

    3

    Plug the side length of the square into the formula. Make sure you are substituting for the variable s.

    • For example, if the square has a side length of 5 centimeters, set up the formula like this:
      d=5{sqrt {2}}

  4. Image titled Calculate a Diagonal of a Square Step 4

    4

    Multiply the length of the side by {sqrt {2}}. This will give you the length of the diagonal. It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round {sqrt {2}} to 1.414.

    5. Advertisement

  1. Image titled Calculate a Diagonal of a Square Step 5

    1

  2. Image titled Calculate a Diagonal of a Square Step 6

    2

    Plug the length of the perimeter into the formula. Make sure you are substituting for the variable P.

    • For example, if the perimeter of the square is 20 centimeters, your formula will look like this:
      20=4s

  3. Image titled Calculate a Diagonal of a Square Step 7

    3

    Solve for s. To do this, divide each side of the equation by 4. This will give you the length of one side of the square.

  4. Image titled Calculate a Diagonal of a Square Step 8

    4

  5. Image titled Calculate a Diagonal of a Square Step 9

    5

    Plug the side length of the square into the formula. Make sure you are substituting for the variable s.

    • For example, if the square has a side length of 5 centimeters, set up the formula like this:
      d=5{sqrt {2}}

  6. Image titled Calculate a Diagonal of a Square Step 10

    6

    Multiply the length of the side by {sqrt {2}}. This will give you the length of the diagonal. It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round {sqrt {2}} to 1.414.

    7. Advertisement

  1. Image titled Calculate a Diagonal of a Square Step 11

    1

  2. Image titled Calculate a Diagonal of a Square Step 12

    2

    Plug the area measurement into the formula. Make sure you are substituting for the variable A.

    • For example, if the area of the square is 25 square centimeters, your formula will look like this:
      25=s^{{2}}

  3. Image titled Calculate a Diagonal of a Square Step 13

    3

    Solve for s. To do this, find the square root of the area. This will give you the length of one side of the square. To find the square root, use a calculator. If you need help calculating the square root by hand, read Calculate a Square Root by Hand.

  4. Image titled Calculate a Diagonal of a Square Step 14

    4

  5. Image titled Calculate a Diagonal of a Square Step 15

    5

    Plug the side length of the square into the formula. Make sure you are substituting for the variable s.

    • For example, if the square has a side length of 5 centimeters, set up the formula like this:
      d=5{sqrt {2}}

  6. Image titled Calculate a Diagonal of a Square Step 16

    6

    Multiply the length of the side by {sqrt {2}}. This will give you the length of the diagonal. *It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round {sqrt {2}} to 1.414.

    7. Advertisement

Calculator, Practice Problems, and Answers

Add New Question

  • Question

    How do I calculate the sides of a square if the diagonal is given?

    Donagan

    First square the diagonal’s length. Divide that by two. Then find the square root of that last number. That’s the side of the square.

  • Question

    How do you find the diagonal of a 24 x 24 foot square?

    Community Answer

    Since you know the length of one side (24) you can use method 1:
    d = s x sqrt*2
    d = 24 x 1.414
    d = 33.936

  • Question

    How do I identify a right angle?

    Community Answer

    You’ll know if an angle is right angle if it is 90 degrees.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

Things You’ll Need

  • Calculator

About This Article

Article SummaryX

To calculate a diagonal of a square, multiply the length of one of the square’s sides by the square root of 2. If you don’t know the length of one side, you can find it by plugging the square’s perimeter into the formula: perimeter = 4s, where s is the length of one side. If you don’t know the perimeter, you can still find the length of one side by plugging the square’s area into the formula: area = s^2, where s is the length of one side. For help solving these formulas, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 758,609 times.

Did this article help you?

Источник

Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.

Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
– Все стороны квадрата равны (от ромба)
– Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)

Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра – диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.

a2+b2=c2
a2+b2=d2
2a2=d2

Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:

d=√(2a2)
d=a√2

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.

Формулы диагонали квадрата через площадь, периметр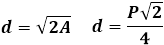

Источник

Длину d диагонали квадрата по отношению к длине b его стороны находят по теореме Пифагора на основании того, что все стороны квадрата равны и все углы, образованные сторонами квадрата, прямые. Поэтому сумма квадратов двух сторон равна квадрату диагонали, являющейся гипотенузой прямоугольного треугольника: 2b^2=d^2, d= b√2. Если принять сторону квадрата за единицу, то d= √2=1,414… .

автор вопроса выбрал этот ответ лучшим

Степа­н-16
[34.5K]

5 лет назад 

Диагональ (с) – это гипотенуза треугольника, у которого катеты (а и а, поскольку они равны) – это две стороны квадрата.

Два способа решения.

  1. По теореме Пифагора: диагональ равна квадратному корню из суммы квадратов сторон.
  2. Через формулы тригонометрии. Диагональ квадрата (гипотенуза треугольника) равна отношению стороны квадрата (или треугольника) к величине 0.707, что есть синус (или косинус, который для 45 град равен синусу) угла в 45град. 45 град – это угол между стороной квадрата и его диагональю.

Алиса в Стран­е
[363K]

5 лет назад 

Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой “а”, а длину гипотенузы латинской буквой “с”, получаем формулу:

c² = a² + a² = 2 a²

с = √2a.

Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон.

Ксарф­акс
[156K]

5 лет назад 

Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины.

В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника.

Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора.

a² + b² = c².

Пусть c – это диагональ, a и b – стороны квадрата, которые по определению равны между собой.

Перепишем формулу в виде:

2a² = c².

Выразим диагональ c:

c = √2 * a.

Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2.

Пример

Сторона квадрата равна 10 см.

Диагональ будет равна 10 * √2 см ≈ 14 см.

terli­4eno4­ka
[75.3K]

5 лет назад 

Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр:

К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле

√2*a = √2*100 = 1,4142*100 = 141,42 см.

Zolot­ynka
[551K]

5 лет назад 

Исходя из того, что, согласно теореме Пифагора, диагональ делит квадрат на два конгруэнтных прямоугольных треугольника, мы можем использовать длину стороны квадрата, чтобы найти длину диагонали (которая будет являться гипотенузой треугольника). Следовательно, d=b√2, где d – длина диагонали, а b – длина одной из сторон.

**

Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07.

**

Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул.

Так же как и найти гипотенузу у равнобедренного треугольника.

Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны.

Имея в условии слово “квадрат” можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй.

Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали.

Alexg­roovy
[14.6K]

5 лет назад 

Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата.

d = √2 * a,

где a – длина стороны квадрата.

d = √2S,

здесь S – площадь квадрата.

d = P / 2√2,

где P – периметр.

Татья­на-Татья­на
[5.4K]

9 лет назад 

На основании теоремы Пифагора – сумма квадратов катетов равна квадрату гипотенузы. То есть, если сторона квадрата равна “а”, то диагональ его (“в”) равна корню квадратному из выражения (2a^2).

То есть вот так:

а^2=b^2+b^2

а^2= 2b^2

a=√2b^2

a=b√2

gemat­ogen
[29.9K]

8 лет назад 

Если взять любой квадрат и принять его сторону за букву – a, то диагональ будет равна √2а.

Это можно вычислить так же по теореме Пифагора, при которой сторона a*a+a*a=2a*a, из этого извлекаем корень и получаем √2а.

Знаете ответ?
Источник

Квадрат – это четырёхугольник, у которого все стороны и углы раны. Он обладает следующими
свойствами:

  • все углы равны между собой и равняются 90;
  • смежные стороны перпендикулярны друг другу;
  • квадрат имеет только две равные диагонали;
  • диагонали в точке пересечения делятся пополам;
  • диагонали перпендикулярны друг другу и являются биссектрисами улов квадрата;
  • радиус описанной окружности равен половине диагонали квадрата;
  • диаметр вписанной окружности равен стороне квадрата.
  • Диагональ квадрата через длину стороны
  • Диагональ квадрата через площадь квадрата
  • Диагональ квадрата через периметр квадрата
  • Диагональ квадрата через радиус описанной окружности
  • Диагональ квадрата через диаметр описанной окружности
  • Диагональ квадрата через радиус вписанной окружности
  • Диагональ квадрата через диаметр вписанной окружности
  • Диагональ квадрата через линию, котороя выходит из угла на
    середину стороны квадрата

Через длину стороны

Чтобы найти диагональ квадрата через длину стороны, необходимо значение стороны а умножить на
квадратный корень из двух. Данная формула выводится из теоремы Пифагора для прямоугольных
треугольников, так как диагональ делит квадрат на два прямоугольных треугольника. Сама диагональ
является гипотенузой данных треугольников. Теорема записывается c² = a² + b², и в данном случае вместо c выступает диагональ d, а вместо
b выступает а, так как катеты равны. Преобразуем: d² = a² + a²; d² = a² * 2. Теперь необходимо извлечь квадратный корень:

D = √(a² * 2)

где D – диагональ квадрата, а – длина стороны.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если сторона квадрата a = 10 см.
Необходимая формула: D = √(a² * 2). Вместо а подставляем значение
10: D = √(10² * 2). После того как находим квадратный корень из двух,
производится умножение и получившееся значение округляем до нужного знака после запятой: D ~ 14,14
см.

Через периметр квадрата

Диагональ квадрата равна отношению периметра P квадрата к произведению четырех на квадратный корень
из двух.

D = P / 4√2

где d – диагональ квадрата, S – периметр квадрата

Цифр после
запятой:

Результат в:

Пример.Необходимо найти диагональ квадрата d, если периметр P = 20 см. Необходимая
формула: D = P / 4√2. Вместо P подставляем значение 20: D = 20 / 4√2.  Получившееся значение округляем до нужного знака после
запятой: D ~ 3,54 см.

Через площадь квадрата

Чтобы найти диагональ квадрата через площадь S, нужно вычислить квадратный корень из произведения S ×
2 . Сама площадь S для прямоугольника имеет формулу S = a * b. Так как
квадрат — это прямоугольник с равными сторонами, формула для площади квадрата S = a². Если
выразить сторону через площадь, формула будет иметь вид: а = √S.

D = √(S * 2)

где D – диагональ квадрата, S – площадь квадрата.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если площадь S = 10 см². Необходимая
формула: D = √(S * 2) Вместо S подставляем значение 10: D = √(10 * 2).  Получившееся значение округляем до нужного знака после
запятой: D ~ 4,47 см.

Через диаметр вписанной окружности

Диагональ квадрата равна произведению диаметра вписанной окружности D на квадратный корень из
двух.

D = d * √2

где D – диагональ квадрата, d – диаметр вписанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если диаметр вписанной окружности d =
10 см. Необходимая формула: D = d * √2. Вместо R подставляем значение 10:
d = 10 * √2. Диагональ равна 14,14 см.

Диагональ квадрата через диаметр описанной окружности

Диагональ квадрата равна диаметру d описанной окружности.

D = d

где D – диагональ квадрата, d – радиус описанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если диаметр описанной окружности d =
10 см. Необходимая формула: d = D. Вместо d подставляем значение
10. Диагональ равна 10 см.

Через радиус описанной окружности

Диагональ квадрата равна радиусу описанной окружности, умноженному на два.

D = 2R

где D – диагональ квадрата, R – радиус описанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности R =
10 см. Необходимая формула: Вместо R подставляем значение 10: D = 2 * 10.
Получившееся значение округляем до нужного знака после запятой: D = 20 см.

Через радиус вписанной окружности

Диагональ квадрата равна произведению удвоенного радиуса вписанной окружности R на квадратный корень
из двух.

D = 2R√2

где D – диагональ квадрата, R– радиус вписанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности D =
10 см. Необходимая формула: D = 2R√2. Вместо R подставляем значение 10:
d = 2 * 10 * √2. Диагональ равна 28,28 см.

Через линию, которая выходит из угла на середину стороны квадрата

Диагональ квадрата равна произведению квадратного корня из восьми пятых и линии C, выходящей из угла
на середину стороны квадрата.

D = √(8/5) * C

где D – диагональ квадрата, C – линия, выходящая из угла на середину квадрата.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата D, если линия, которая проходит из угла
на середину стороны квадрата С = 10 см. Необходимая формула: D = √(8/5) * C. Вместо R подставляем значение 10: D = √(8/5) * 10. Диагональ
равна 12,64 см.

Источник

Добавить комментарий