Загрузить PDF
Загрузить PDF
Диагональ квадрата — это отрезок, который соединяет противолежащие углы квадрата и проходит через его центр. Чтобы вычислить диагональ квадрата, воспользуйтесь формулой 
, где 
— сторона квадрата. В задачах требуется найти диагональ квадрата по данному значению другой величины, например, периметра или площади. В этих случаях необходимо использовать другие формулы, чтобы сначала вычислить сторону квадрата, а потом – его диагональ.
-
1
Найдите длину стороны квадрата. Скорее всего, значение длины стороны квадрата будет дано в условии задачи. Если же вы работаете с реальным предметом, измерьте его сторону при помощи линейки или рулетки. Так как у квадрата все стороны равны, измерьте или найдите длину любой стороны. Если длина стороны квадрата неизвестна, этим методом пользоваться нельзя.
- Например, дан квадрат со стороной 5 см.
-
2
-
3
Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо
.
- Например, если сторона квадрата равна 5 см, формула запишется так:
- Например, если сторона квадрата равна 5 см, формула запишется так:
-
4
Умножьте сторону квадрата на
, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите до 1,414.
Реклама
-
1
-
2
Подставьте в формулу значение периметра квадрата. То есть данное значение нужно подставить вместо
.
- Например, периметр квадрата равен 20 см. Запишите формулу так:
- Например, периметр квадрата равен 20 см. Запишите формулу так:
-
3
Найдите
. Для этого разделите каждую сторону уравнения на 4. В результате будет вычислена сторона квадрата.
-
4
-
5
Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо
.
- Например, если сторона квадрата равна 5 см, формула запишется так:
- Например, если сторона квадрата равна 5 см, формула запишется так:
-
6
Умножьте сторону квадрата на
, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите до 1,414.
Реклама
-
1
-
2
В формулу подставьте значение площади квадрата. То есть данное значение нужно подставить вместо
.
- Например, площадь квадрата равна 25 см2. Запишите формулу так: .
- Например, площадь квадрата равна 25 см2. Запишите формулу так:
-
3
Найдите
. Для этого извлеките квадратный корень из значения площади квадрата. В результате будет вычислена сторона квадрата. Воспользуйтесь калькулятором, чтобы извлечь квадратный корень. Если квадратный корень нужно извлечь вручную, прочитайте эту статью.
-
4
-
5
Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо
.
- Например, если сторона квадрата равна 5 см, формула запишется так:
- Например, если сторона квадрата равна 5 см, формула запишется так:
-
6
Умножьте сторону квадрата на
, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите до 1,414.
Реклама
Что вам понадобится
- Калькулятор
Об этой статье
Эту страницу просматривали 424 771 раз.
Была ли эта статья полезной?
Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.
Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
– Все стороны квадрата равны (от ромба)
– Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)
Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра – диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.
a2+b2=c2
a2+b2=d2
2a2=d2
Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:
d=√(2a2)
d=a√2
Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.
Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.
Формулы диагонали квадрата через площадь, периметр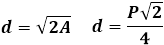 
|
Длину d диагонали квадрата по отношению к длине b его стороны находят по теореме Пифагора на основании того, что все стороны квадрата равны и все углы, образованные сторонами квадрата, прямые. Поэтому сумма квадратов двух сторон равна квадрату диагонали, являющейся гипотенузой прямоугольного треугольника: 2b^2=d^2, d= b√2. Если принять сторону квадрата за единицу, то d= √2=1,414… . автор вопроса выбрал этот ответ лучшим
Степан-16 5 лет назад Диагональ (с) – это гипотенуза треугольника, у которого катеты (а и а, поскольку они равны) – это две стороны квадрата. Два способа решения.
Алиса в Стране 5 лет назад Если поделить квадрат диагональю, то мы увидим перед собой два одинаковых прямоугольных треугольника, а диагональ квадрата будет для любого из этих треугольников гипотенузой. А как рассчитывать длину гипотенузы, зная длину катетов, мы все знаем. Для этого у нас имеется теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Катеты у нас равны друг другу (потому что у нас квадрат), значит, обозначив длину катета латинской буквой “а”, а длину гипотенузы латинской буквой “с”, получаем формулу: c² = a² + a² = 2 a² с = √2a. Ответ: диагональ квадрата равна квадратному корню из суммы квадратов его сторон.
Ксарфакс 5 лет назад Диагональ квадрата представляет собой отрезок, соединяющий две противоположные вершины. В то же время диагональ разбивает квадрат на 2 равных прямоугольных треугольника. Таким образом, чтобы найти диагональ квадрата, следует воспользоваться теоремой Пифагора. a² + b² = c². Пусть c – это диагональ, a и b – стороны квадрата, которые по определению равны между собой. Перепишем формулу в виде: 2a² = c². Выразим диагональ c: c = √2 * a. Таким образом, диагональ квадрата равна произведению его стороны на квадратный корень из числа 2.
Пример Сторона квадрата равна 10 см. Диагональ будет равна 10 * √2 см ≈ 14 см.
terli4eno4ka 5 лет назад Под диагональю квадрата понимается отрезок, соединяющий противоположные углы квадрата. Для того, чтобы найти диагональ квадрата, можно воспользоваться следующими формулами, для которых нужно знать, чему равна сторона квадрата, площадь или периметр:
К примеру, если у нас есть квадрат со сторонами 100 см, то его диагональ будет по формуле √2*a = √2*100 = 1,4142*100 = 141,42 см.
Zolotynka 5 лет назад Исходя из того, что, согласно теореме Пифагора, диагональ делит квадрат на два конгруэнтных прямоугольных треугольника, мы можем использовать длину стороны квадрата, чтобы найти длину диагонали (которая будет являться гипотенузой треугольника). Следовательно, d=b√2, где d – длина диагонали, а b – длина одной из сторон. ** Например, если длина стороны квадрата 5 сантиметров, то, согласно нашей формуле, длина диагонали будет: d=5√2, или d=5*1,414=7,07. ** Длину диагонали можно узнать, если известны, например, площадь или периметр квадрата. В этом случае придется использовать сразу несколько формул.
Так же как и найти гипотенузу у равнобедренного треугольника. Квадрат это правильная геометрическая фигура, имеющая четыре равных стороны. Имея в условии слово “квадрат” можно вообще найти его диагональ по одной стороне, ибо все остальные будут равные ёй. Длину одной из сторон, умножить её на два и возвести в квадрат. Результатом и будет квадрат диагонали.
Alexgroovy 5 лет назад Диагональ квадрата принято рассчитывать, оперируя понятиями сторона, площадь и периметр. Имея эти данные легко воспользоваться формулами для расчета диагонали квадрата. d = √2 * a, где a – длина стороны квадрата. d = √2S, здесь S – площадь квадрата. d = P / 2√2, где P – периметр.
Татьяна-Татьяна 9 лет назад На основании теоремы Пифагора – сумма квадратов катетов равна квадрату гипотенузы. То есть, если сторона квадрата равна “а”, то диагональ его (“в”) равна корню квадратному из выражения (2a^2). То есть вот так: а^2=b^2+b^2 а^2= 2b^2 a=√2b^2 a=b√2
gematogen 8 лет назад Если взять любой квадрат и принять его сторону за букву – a, то диагональ будет равна √2а. Это можно вычислить так же по теореме Пифагора, при которой сторона a*a+a*a=2a*a, из этого извлекаем корень и получаем √2а. Знаете ответ? |
Из школьного курса математики мы знаем, что квадрат — это четырёхугольник у которого все углы прямые, а все стороны равны.
Диагональ — отрезок, соединяющий две противоположные вершины квадрата. Задача нахождения диагонали квадрата может встретиться и после окончания школы. К примеру, при постройке дома у которого фундамент должен быть квадратным. Когда размечается фундамент, мало убедиться, что все 4 стороны равны. Ведь у ромба тоже все стороны равны. И получить ромбовидный фундамент вряд ли кто захочет.
В этом случае, чтобы убедиться в том, что фундамент действительно представляет собой квадрат, вычисляют диагональ квадрата и измеряют обе диагонали фундамента. Если все 4 стороны равны между собой и две диагонали также имеют одинаковую длину — фундамент точно будет квадратным. Для вычисления длины диагонали квадрата достаточно знать длину его стороны и простую формулу.
Как найти диагональ квадрата
d=a cdot sqrt{2}
d — диагональ квадрата
a — сторона квадрата
Достаточно подставить в формулу длину стороны квадрата вместо a.
А можно воспользоваться нашим калькулятором. Просто введите длину стороны и тут же получите длину диагонали квадрата. У нас также можно найти диагональ прямоугольника.
Диагональ квадрата онлайн
Примеры нахождения диагонали квадрата
Найдем диагональ квадрата со стороной 3 см.
Подставим в формулу вместо a число 3 и получим d=3 cdot sqrt{2} = sqrt{3^2 cdot 2} = sqrt{18} = 4,24264
Найдем диагональ квадрата со сторонами 2 на 2 см.
Подставим в формулу вместо a число 3 и получим d=2 cdot sqrt{2} = sqrt{2^2 cdot 2} = sqrt{8} = 2,828427
Ваша оценка
[Оценок: 284 Средняя: 2.9]
Диагональ квадрата формула и расчет Автор admin средний рейтинг 2.9/5 – 284 рейтинги пользователей
Укажите размеры:
Диагональ:
Решение:
Ссылка на страницу с результатом:
# Теория
Квадрат – это четырёхугольник у которого все стороны равны и все углы прямые.
Диагональ квадрата – это прямой отрезок соединяющий противоположные вершины квадрата. Поскольку у квадрата все стороны равны, диагональ делит квадрат на два равных прямоугольных треугольника.
Формула расчёта диагонали квадрата
Если известна длина стороны квадрата, можно использовать теорему Пифагора для вычисления длины диагонали.
a
d
d = a cdot sqrt{2}
- d – диагональ квадрата
- a – сторона квадрата
Свойства диагонали квадрата
- Диагонали квадрата равны (имеют одинаковую длину).
- Диагональ квадрата разделяет его на два равных треугольника.
- Диагональ квадрата служит гипотенузой прямоугольного треугольника, образованного двумя его сторонами. Другие две стороны треугольника являются катетами, которые являются сторонами квадрата.
- Диагональ квадрата является самым длинным отрезком внутри квадрата.
- Диагональ делит угол квадрата пополам.
- Диагонали квадрата пересекаются в его центре и образуют прямые углы.
- Диагональ является диаметром вписанной окружности.
- Диагональ квадрата делит его на две равные площади. Каждая половина квадрата, образованная диагональю, имеет площадь, равную половине площади всего квадрата.
Похожие калькуляторы:
Войдите чтобы писать комментарии
