Диагональ треугольника


4.7
Средняя оценка: 4.7
Всего получено оценок: 78.
4.7
Средняя оценка: 4.7
Всего получено оценок: 78.
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
- Высота;
- Медиана;
- Биссектриса.
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует
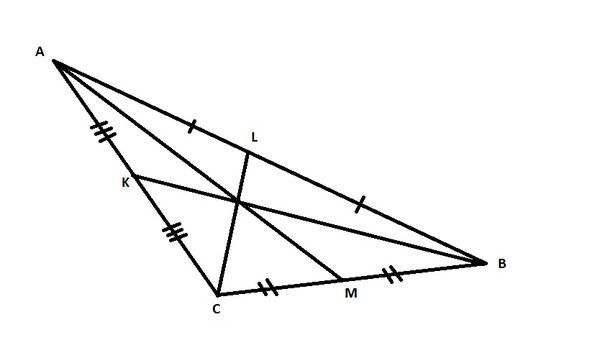
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P={n(n-3)over{2}}$ – где n это число сторон многоугольника.
Проверим для квадрата:
$P={4(4-3)over{2}}={4over2}=2$ – все верно.
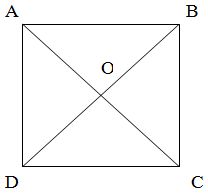

Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Алексей Касюгин
4/5
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 78.
А какая ваша оценка?
Треугольник
Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.
Найти длину диагонали и углы прямоугольника
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
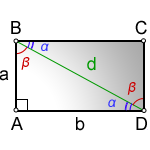
d – диагональ прямоугольника
a , b – стороны
α , β – углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, ( d ):
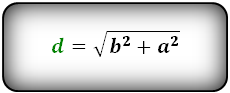
Формулы диагонали через сторону и угол, ( d ):
Формулы величины углов через диагональ и стороны, ( α , β ) :
2. Формулы углов между диагоналями в прямоугольнике.
d – диагонали прямоугольника
a , b – стороны
α , β – углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, ( α , β ):
Диагональ треугольника – формула
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует
Рис. 1. Три медианы в треугольнике.
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.
Рис. 2. Диагонали многоугольника.
В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P=>$ – где n это число сторон многоугольника.
Проверим для квадрата:
Рис. 3. Диагонали квадрата.
Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
[spoiler title=”источники:”]
http://www-formula.ru/rectangle-formula
http://sprint-olympic.ru/uroki/matematika-uroki/15430-diagonal-treygolnika-formyla.html
[/spoiler]
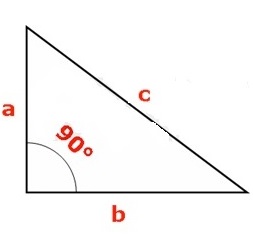
If your teacher has asked you to calculate the diagonal of a triangle, she’s already given you some valuable information. That phrasing tells you that you’re dealing with a right triangle, where two sides are perpendicular to each other (or to say it another way, they form a right triangle) and only one side is left to be “diagonal” to the others. That diagonal is called the hypotenuse, and you can find its length using the Pythagorean Theorem.
TL;DR (Too Long; Didn’t Read)
To find the length of the diagonal (or hypotenuse) of a right triangle, substitute the lengths of the two perpendicular sides into the formula a2 + b2 = c2, where a and b are the lengths of the perpendicular sides and c is the length of the hypotenuse. Then solve for c.
Pythagoras’ Theorem
The Pythagorean Theorem – sometimes also called Pythagoras’ Theorem, after the Greek philosopher and mathematician who discovered it – states that if a and b are the lengths of the perpendicular sides of a right triangle and c is the length of the hypotenuse, then:
a^2 + b^2 = c^2
In real-world terms, this means that if you know the length of any two sides of a right triangle, you can use that information to find out the length of the missing side. Note that this only works for right triangles.
Solving for the Hypotenuse
Assuming you know the lengths of the two non-diagonal sides of the triangle, you can substitute that information into the Pythagorean Theorem and then solve for c.
-
What if you know the length of the triangle’s diagonal and one other side? You can use the same formula to solve for the length of the unknown side. Just substitute in the lengths of the sides you do know, isolate the remaining letter variable on one side of the equals sign, and then solve for that letter, which represents the length of the unknown side.
Substitute the known values of a and b – the two perpendicular sides of the right triangle – into the Pythagorean Theorem. So if the two perpendicular sides of the triangle measure 3 and 4 units respectively, you’d have:
3^2 + 4^2 = c^2
Work the exponents (when possible – in this case you can) and simplify like terms. This gives you:
9 + 16 = c^2
Followed by:
c^2 = 25
Take the square root of both sides, the final step in solving for c. This gives you:
c = sqrt{25}= 5
So the length of the diagonal, or hypotenuse, of this triangle is 5 units.
Tips
Расчет диагонали
Расчет диагонали
Скачать, сохранить результат
Выберите способ сохранения
-
Вы можете сохранить результат расчёта в формате PDF на ваше устройство.
-
Распечатайте результат расчёта конструкции на бумагу любого формата.
-
Отправьте результат расчета в формате PDF на ваш е-мейл.
Информация
Профессиональное проектирование и формирование фундамента, стен, а также полноценной системы крыши дома требует чёткого выставления геометрических углов и расчёта диагоналей сегментов конструкций. От точности вычислительных манипуляций напрямую зависит безопасность, устойчивость, прочность и долговечность здания. Интерактивный калькулятор диагоналей для расчёта фундамента и крыш поможет безошибочно выполнить все расчётные операции на этапе проектирования дома всего за несколько секунд.
Преимущества калькулятора диагоналей
- Помогает безошибочно рассчитать квадрат конкретной секции фундамента всего в несколько кликов.
- Позволяет самостоятельно выполнить расчёт диагонали прямоугольника или треугольника.
- Помогает быстро рассчитать общую длину и ширину фундамента, а также стен дома.
- Результаты расчётных операций гарантируют чёткое выставление геометрических углов в 90° при монтаже конструкционных элементов фундамента, стен и крыши.
- Экономит уйму времени, сил нервов и средств в процессе проектирования строений всех категорий.
- Расчёт диагоналей основания обеспечивает безупречное обустройство фундамента, что дарит дому безопасность, надёжность и долговечность.
- Возможность бесплатно получить результаты расчётных операций в формате PDF на свой E-mail или мгновенно распечатать их в режиме онлайн.
Безошибочно рассчитайте геометрические параметры фундамента, стен и конструкционных элементов системы крыши уже сегодня. Бесплатно задействуйте онлайн калькулятор диагоналей — сэкономьте силы, время и деньги прямо сейчас!
Добавить комментарий
Если учитель попросил вас вычислить диагональ треугольника, она уже дала вам некоторую ценную информацию. Эта фраза говорит вам, что вы имеете дело с прямоугольным треугольником, две стороны которого перпендикулярны каждой. другие (или, говоря по-другому, они образуют прямоугольный треугольник), и только одна сторона осталась «диагональной» по отношению к другие. Эта диагональ называется гипотенузой, и вы можете найти ее длину с помощью теоремы Пифагора.
TL; DR (слишком длинный; Не читал)
Чтобы найти длину диагонали (или гипотенузы) прямоугольного треугольника, подставьте длины двух перпендикулярных сторон в формулуа2 + б2 = c2, гдеаа такжеб– длины перпендикулярных сторон иcдлина гипотенузы. Затем решите дляc.
Теорема Пифагора
Теорема Пифагора – иногда также называемая теоремой Пифагора в честь открывшего ее греческого философа и математика – утверждает, что еслиаа такжеб– длины перпендикулярных сторон прямоугольного треугольника иc– длина гипотенузы, тогда:
а ^ 2 + Ь ^ 2 = с ^ 2
В реальных условиях это означает, что если вы знаете длину любых двух сторон прямоугольного треугольника, вы можете использовать эту информацию, чтобы определить длину недостающей стороны. Обратите внимание, что это работает только для прямоугольных треугольников.
Решение гипотенузы
Предполагая, что вам известны длины двух недиагональных сторон треугольника, вы можете подставить эту информацию в теорему Пифагора, а затем решить дляc.
-
Что, если вы знаете длину диагонали треугольника и одну другую сторону? Вы можете использовать ту же формулу для определения длины неизвестной стороны. Просто подставьте длины сторон, которые вы знаете, изолируйте оставшуюся буквенную переменную на одной сторону знака равенства, а затем решите эту букву, которая представляет длину неизвестного боковая сторона.
Подставьте известные значенияаа такжеб– две перпендикулярные стороны прямоугольного треугольника – в теорему Пифагора. Итак, если две перпендикулярные стороны треугольника имеют размер 3 и 4 единицы соответственно, у вас будет:
3 ^ 2 + 4 ^ 2 = с ^ 2
Работайте с экспонентами (если возможно – в данном случае можете) и упростите подобные термины. Это дает вам:
9 + 16 = с ^ 2
С последующим:
с ^ 2 = 25
Извлеките квадратный корень из обеих частей, это последний шаг в решении дляc. Это дает вам:
c = sqrt {25} = 5
Таким образом, длина диагонали или гипотенузы этого треугольника равна 5 единицам.
Советы
Teachs.ru
