По
известному дирекционному углу n
и по исправленным горизонтальным углам
испр
вычисляются дирекционные углы остальных
сторон теодолитного хода по формулам
для правых горизонтальных углов:
– дирекционный
угол последующей стороны равен
дирекционному углу предыдущей стороны
плюс 180
и минус исправленный горизонтальный
угол правый по ходу.
Величина
дирекционного угла не может превышать
360
и быть меньше 0.
Если величина дирекционного угла больше
360,
то из результата вычислений необходимо
вычесть 360
(см. пример).
Контроль
вычисления дирекционных углов. В
замкнутом теодолитном ходе в результате
вычислений получается дирекционный
угол исходной стороны.
Пример вычисления дирекционных углов: Дирекционный угол исходной стороны 1-2 равен 4545.
;
;
;
;
При
вычислении дирекционного угла получилось
значение 40545.
Из полученного значения вычитается
360.
.
Контроль
вычисления дирекционных углов получился.
Все
результаты вычислений заносятся в
таблицу «Ведомость вычисления координат»
(табл. 6).
3.3 Вычисление приращений координат
Вычисление
приращений координат выполняется по
формулам:
,
где
d
– горизонтальное проложение (длина)
линии;
– дирекционный угол этой линии.
Приращения
координат вычисляются с точностью два
знака после запятой.
Пример вычисления приращений координат:
;
;
;
;
.
;
;
;
;
.
Все
результаты вычисления заносятся
в табл. 6. Пример
вычисления тригонометрических функций
на калькуляторе приведен в
прил. 3.
3.4 Уравнивание линейных измерений
Разность
между суммой вычисленных приращений
координат и теоретической суммой
называется линейной невязкой хода и
обозначается fХ
и fY.
Уравнивание линейных измерений
выполняется по осям Х
и Y.
Линейная невязка
вычисляется по формулам:
.
Теоретическая
сумма приращений координат зависит от
геометрии хода. В замкнутом теодолитном
ходе она равна нулю, тогда невязка равна
.
Прежде,
чем распределять невязки в приращения
координат, необходимо убедиться в их
допустимости. Для чего вычисляется
абсолютная невязка хода fабс
и
относительная
,
где
Р
– периметр хода (сумма длин сторон), м.
Относительная
невязка сравнивается с допустимой
.
В
случае, когда полученная относительная
невязка допустима, т.е.
,
то вычисляются поправки в приращения
координат пропорционально
длинам сторон.
Невязки распределяются с обратным
знаком. Если
,
то проверяются вычисления в п.
3.3 и 3.4.
Поправки
в приращения координат X
и Y
вычисляются
по формулам с округлением до 0,01 м:
,
где
X
и Y
– поправка
в приращение по оси Х
и
Y,
соответственно, м; fX
и fY
–
невязки
по осям, м; Р
–
периметр
(сумма сторон), м; di
–
измеренная
длина (горизонтальное проложение), м.
Знак
у поправки противоположен знаку невязки.
Поправки записываются в «Ведомость
вычисления координат». В примере (табл.
6) поправки показаны красным цветом.
После
вычисления поправок следует сделать
проверку, т.е. сложить все поправки. Если
их сумма будет равна невязке с обратным
знаком, то распределение невязки
выполнено правильно. То есть:
.
Вычисляются
исправленные приращения.
Полученные
поправки алгебраически прибавляются
к соответствующим приращениям и
получаются исправленные приращения:
.
Контроль:
сумма исправленных приращений в замкнутом
теодолитном ходе должна равняться нулю,
т.е. должно выполняться равенство:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы понять, что такое дирекционный угол, представим на карте линию (отрезок) с начальной точкой А и конечной точкой В.
Теперь проведем из начала отрезка (точки А) луч, параллельный осевому меридиану зоны и направленный на север. И будем поворачивать этот
луч вокруг точки А по часовой стрелке до тех пор, пока он не пересечется с точкой В. Угол, на который мы повернули луч,
и будет называться дирекционным углом линии АВ.
Калькулятор угла по координатам
С помощью этого калькулятора Вы сможете производить расчет дирекционных углов линий на основе заданных координат точки стояния (А) и точки
ориентирования (В), а также рассчитывать расстояние между этими точками.
Калькулятор координат по углу и расстоянию
Этот калькулятор поможет Вам рассчитать координаты конечной точки пути на основе координат начальной точки, дирекционного угла и расстояния между точками.
Угол можно указывать как в десятичных градусах (226,27303°), так и в градусах – минутах – секундах (226° 16′ 22″).
Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. Т.е. при известных координатах точек А(XA, YA) и В(XB, YB) необходимо найти длину SAB и направление линии АВ: осевой румб rAB и дирекционный угол aAB (рис. 10).
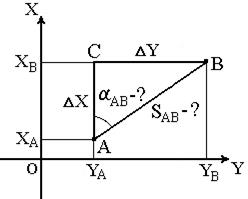Координаты точекА(XA, YA) и В(XB, YB) определяют при решении предыдущей задачи (см. п.1.4.2).
Данная задача решается следующим образом.
Рис. 10. Обратная геодезическая задача
.
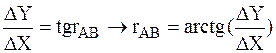По знакам приращений координат определяем четверть, в которой располагается румб, и её название (см. табл.1).
Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим aAB.
Рис. 11. Осевые румбы и дирекционные углы
Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:
IV четверть (СЗ) r = 360° – a .
.
.
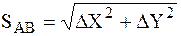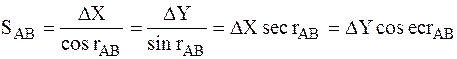В(6000.150 км, 2395.250 км).
.
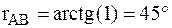Лучшие изречения:
Лаской почти всегда добьешься больше, чем грубой силой. © Неизвестно
==> читать все изречения. 356 — 
| 314 — 
Источник
Вычисление исходных дирекционных углов линий; решение прямой геодезической задачи.
Правый угол при т. В (между сторонами АВ и ВС) β1=189º 59,2´;
Правый угол при т. С (между сторонами ВС и СD) β2=159º 28,0´;
Найти: дирекционные углы линии ВС и СD, если известны дирекционный угол αАВ линии АВ и измеренные по правому ходу углы β1 и β2.
Дирекционный угол вычисляется по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус горизонтальный угол, справа по ходу лежащий
αВС = αАВ +180º — β1;
αСD = αВС +180º — β2;
αВС = 97º 38,2´+ 180º — 189º 59,2´=87º39,0´
αСD = 87º 39,0´+180º — 159º 28,0´ = 108º 11,0´
Рис.1. Схема теодолитного хода
Ответ: дирекционные углы αВС = 87º 39,0´ и αСD = 108º 11´.
координаты т. В хВ = — 14,02 м,
Найти: координаты хС и YС т.С, если известны координаты хВ и yВ т.В, длинна dВС линии ВС и дирекционный угол αВС этой линии.
Координаты т.С вычисляются по формулам
yС = yВ + ΔyВС; где ΔхВС и ΔyВС – приращение координат и вычисляются
Знаки вычисленных приращений координат определяем по названию румба руководствуясь таблицей: Перевод дирекционных углов в румбы. Знаки приращений координат.
ΔхВС = dВС cos αВС
ΔхВС = 239,14 cos 87º 39,0´
ΔyВС = dВС sin αВС
ΔyВС = 239,14 sin 87º 39,0´
Перевод дирекционных угол в румбы. Знаки приращений координат.
Источник
7.1 Графический способ измерения дирекционного угла
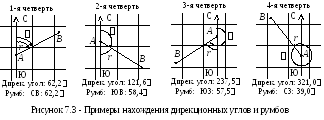
Н
а карте дирекционные углы измеряют или откладывают от линий координатной сетки с помощью транспортира (рисунок 7.3). При этом не обязательно (и не нужно) через начальную точку проводить линию, параллельную линиям сетки. Измеряют нужные углы в точке пересечения линииАВ и линий сетки (рисунок 7.4). Если искомая линия, например CD, не пересекает ни одной вертикальной линии сетки, то измерения можно выполнить от горизонтальной линии сетки, изменив затем измеренный угол на 90. Есть варианты измерений и не показанные на рисунке.
7.2 Аналитический способ. Обратная геодезическая задача
Дирекционный угол АВ линии АВ и расстояние dАВ между точками А и В можно найти из решения обратной геодезической задачи. В задаче исходными являются координаты xA и yA начальной точки А и координаты xB и yB конечной точки В (рисунок 7.5).
Вначале вычисляют приращения координат
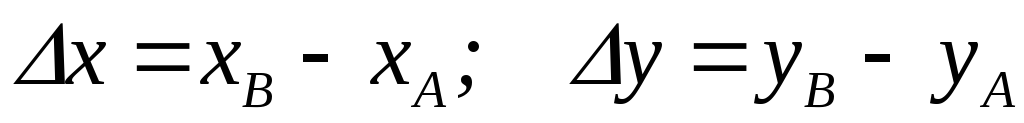. (8.1)
Дирекционный угол находят одним из двух способов.
Вычисляют румб отрезка АВ, взяв абсолютные значения x и y.
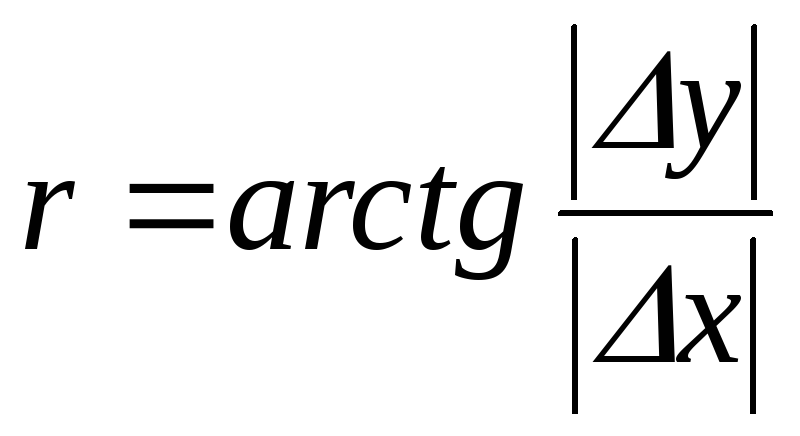. (8.2)
Затем в зависимости от знаков x и y выбирают из таблицы 7.1 нужную формулу перехода к дирекционному углу.
Таблица 7.1 – Переход от румба к дирекционному углу
Знаки приращений координат
Формула перехода к дирекционному углу
Способ 2
Вычисляют с учётом знаков x и yвспомогательный угол
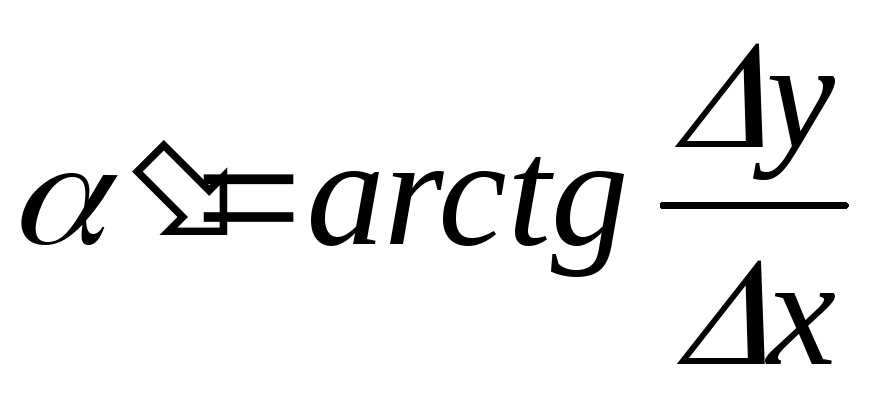, (8.3)
который лежит в диапазоне от -90 до +90.
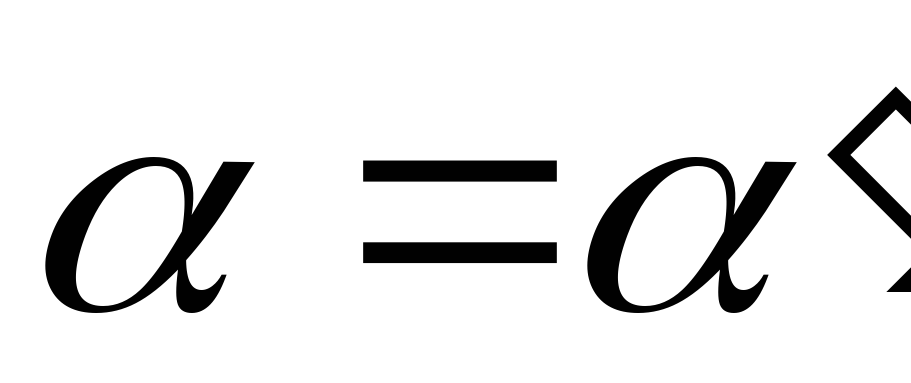, если 
. (если
, то
);
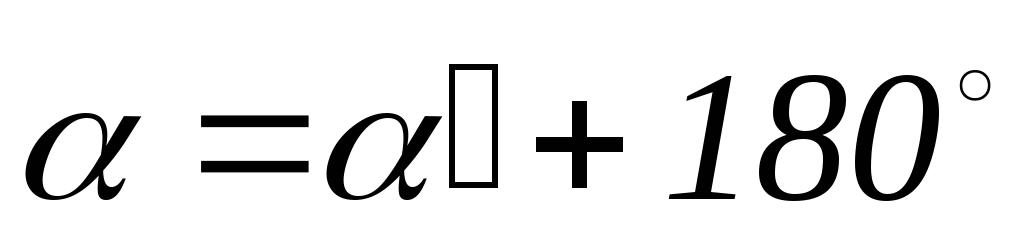, если 
.
Способ 1 применяют тогда, когда функцию арктангенса находят по таблицам, а способ 2 – когда функцию арктангенса вычисляют на калькуляторе.
Расстояниемежду точками А и В вычисляют по одной из трёх формул
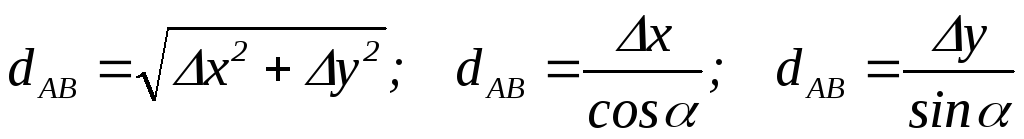. (8.4)
Первая формула предпочтительней, если используют калькулятор, у которого имеется функция извлечения квадратного корня. Две другие формулы можно использовать для контроля вычислений как расстояния dAB, так и дирекционного угла AB.
Задание 11. Измерить на рисунках 4.6 или 4.7 дирекционный угол с первой точки на вторую точку и расстояние между ними. Вычислить румб направления. Для задания взять те же точки, для которых определены координаты (см. задание 3). Затем по прямоугольным координатам решить обратную геодезическую задачу и сравнить между собой результаты вычислений с измеренными величинами.
8 Вычисление истинных и магнитных азимутов
Истинный азимут – это угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до ориентируемой линии. Магнитный азимут отсчитывают от магнитного меридиана.
Т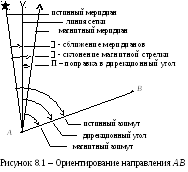
ри ориентирующих угла – истинный азимутА, дирекционный угол и магнитный азимут АМ , отсчитываемые от соответствующих начальных направлений – истинного меридиана, линии сетки и магнитного меридиана, связаны между собой тремя углами – сближением меридианов , склонением магнитной стрелки и поправкой в дирекционный угол П. На рисунке 8.1 показаны положительные значения углов , и П. Последний угол П используется редко и рассматривать его не будем. Положительным углам и соответствует отклонение на восток линии сетки и магнитного меридиана относительно истинного меридиана.
Указанная зависимость выражается формулами
.
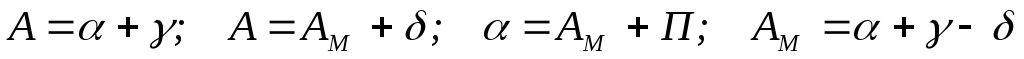Истинный азимут направления на карте обычно вычисляют по указанной формуле, хотя его можно и измерить непосредственно. Для этого нужно через начальную точку провести истинный меридиан, который параллелен рамке карты. Магнитный азимут всегда вычисляют. Для этого можно использовать указанные внизу карты взаимное положение трёх начальных направлений, углы между ними и пояснения. Магнитный азимут на местности измеряют с помощью буссоли.
Задание 12. Вычислить по последней цифре кода k студента сближение меридианов и склонение магнитной стрелки
.
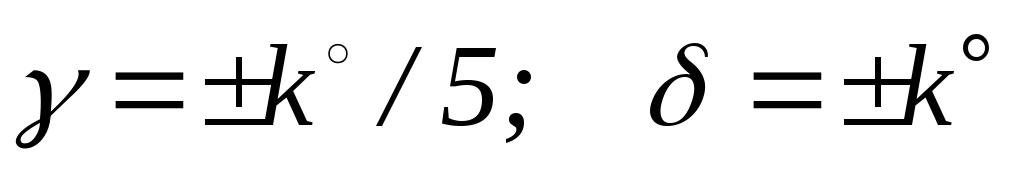Верхние знаки взять для чётной предпоследней цифры кода студента, нижние знаки – для нечётной цифры.
Нарисовать взаимное расположение трёх начальных направлений для указанных данных. Вычислить истинный и магнитный азимуты по дирекционному углу, взятому из задания 11.
Источник
1) Нахождения приращений:
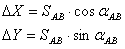
2) Нахождения координат:
Обратная геодезическая задача в прямоугольных кординатах
Обратная геодезическая задача (ОГЗ) заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.
В зависимости от длины геодезической линии, соединяющей рассматриваемые точки, применяются различные методы и формулы, разработанные в геодезии. По размерам принятого земного эллипсоида (см. Эллипсоид Красовского) составляются таблицы, облегчающие решение геодезических задач и рассчитанные на использование определённой системы формул.
В обратной геодезической задаче находят дирекционный угол и расстояние:
1) Вычисляют румб по формуле:
2) Находят дирекционный угол в зависимости от четверти угла:
3) Определяют расстояние между точками:
Изображение рельефа местности на планах и картах
Поверхность нашей планеты неровная. Эти неровности земной поверхности называются рельефом. Для того чтобы на плане изобразить его, необходимо знать прежде всего абсолютную высоту каждой точки поверхности.
Абсолютной высотой называют высоту места над уровнем океана. В России абсолютная высота отсчитывается от уровня Балтийского моря, принимаемого за 0 м. В городе Кронштадте, расположенном на одном из островов в Балтийском море, располагается футшток — рейка с делениями. Абсолютная высота отсчитывается от нуля этого футштока. Эта высота может быть положительной или отрицательной. Если точка лежит выше уровня моря, то ее высота считается положительной (холмы, возвышенности, горы), а если ниже — отрицательной (океанические впадины). Отрицательную абсолютную высоту могут иметь и точки на суше (Прикаспийская низменность). На планах и картах абсолютная высота обозначается точкой, около которой помещают число метров. Такое обозначение называют отметкой высоты. Разность абсолютных высот точек показывает относительную высоту, то есть превышение одной точки земной поверхности относительно другой.
В разных частях Мирового океана, хотя все они соединяются как сообщающиеся сосуды, уровни не одинаковые. Так, уровень океана у Кронштадта выше, чем уровень вод Тихого океана у Владивостока, на 1,8 м. Причин этого несколько; одна из них связана с процессами, происходящими во время приливов и отливов. Для практических целей пользуются средним многолетним уровнем, который принимается за исходный.
Основные формы рельефа и изображение их горизонталями.
Под рельефом местности понимают совокупность неровностей земной поверхности.
На топографических планах рельеф изображется горизонталями (0,1-0,15мм) кривыми. Расстояние между соседними горизонталями по высоте называется сечением рельефа. В плане золожением для большей выразительности рельефа каждая 4-я четная по высоте 5м(сечения через 0,5) иля 5-я кратная высоте h=1м горизонталь утолщается и проводится t=0,25мм и в разрыве подписывается ее высота.
Основанием цифры в сторону понижения рельефа.
Направление ската склона обозначается берх-штрихами – черточками длина чрточки 0,5мм.
Для указания высот горизонталей их отметки подписывают в разрывах утолщенных 0,25мм горизонталей распологая основание цифр вниз по рельефу.
Различают следующие формы рельефа:
1). гора-куплообразная возвышенность (выше 200м)
2).Котловина (чашеобразное углубление)
3). Хребет – возвышенность вытянутой формы с постепенным понижением имеет водораздельную линию
4). Лощина – вытянутое углубление местности постепенно понижающиеся. Имеет водозборнную линию
5). Седоловина – понижение местности между соседними возвышенностями
Сущность изображения рельефа местности горизонталями.
Крутизна и направление ската, графики заложений для углов наклона и уклонов.
Источник
Adblock
detector
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2016 года; проверки требуют 106 правок.
6-градусные зоны В Проекции Гаусса — Крюгера
1-я четверть n-градусной зоны и линии параллельный осевому меридиану
Дирекционный угол — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением осевого меридиана зоны прямоугольных координат и направлением на ориентир. Дирекционные углы направлений измеряются преимущественно по карте.[1]
Вся земная поверхность, будучи шарообразной, не может быть перенесена на плоскость без разрывов и искажений. Поэтому её разделили на равные части ограниченные меридианами с разностью долгот в n градусов, имеющие наименование n-градусной координатной зоны. В каждой такой зоне за вертикальную ось координат (ось Х) принят осевой меридиан. Горизонтальная ось Y дополняет систему до правой и служит во всех зонах линией экватора. Пересечение осей в каждой зоне принимается за начало координат. Значение координат Х положительными считается к северу от линии экватора (OY). Угол по ходу часовой стрелки от 0° до 360° между северным направлением оси Х (вертикальной линией километровой сетки) и направлением на предмет является Дирекционным углом.[2]
Дирекционные углы применяются при выполнении засечек или прокладке полигонометрического хода путём передачи угловых измерений от направления с известным дирекционным углом к искомым.
[3]
Не стоит путать дирекционный угол и пеленг.
Взаимосвязь Дирекционного угла с прочими углами ориентирования[править | править код]
Шкалы географических координат и километровая сетка на карте масштабом 1:25000. Сопоставление угловых и прямоугольных координат
Дирекционные углы направлений могут определяться геодезическим, магнитным, астрономическим и гироскопическим способами, а также методами космической геодезии.
Магнитный азимут[править | править код]
Магнитный способ заключается в определении с помощью магнитной стрелки компаса (буссоли) и по данным о склонении магнитной стрелки.[3]
Приближенные значения дирекционных углов направлений (
) с точностью порядка 10-25 угловых минут могут быть вычислены из значения магнитного азимута направления (
), который определен с помощью компаса или ориентир-буссоли, которая входит в комплект дополнительного оборудования теодолитов и тахеометров. Ориентир-буссоль предназначена для определения магнитных азимутов направлений (с точностью 1-60 угловых секунд). Для перехода от магнитного азимута к дирекционному углу необходимо знать Склонение магнитной стрелки (
), которое определяется, как правило, на исходном геодезическом пункте в районе выполнения работ и указана на топографических картах.
Географический азимут[править | править код]
Географический азимут – является дирекционным углом.
Геодезический румб[править | править код]
Связь между Геодезический румбом и дирекционным углом устанавливается по формулам:
I Четверть – 
II Четверть 
III Четверть 
IV четверть 
Навигационный румб[править | править код]
Связь между Навигационный и дирекционным углом устанавливается по формуле:
– уход магнитной стрелки влево относительно норда
+ уход магнитной стрелки вправо относительно норда
Сближение меридианов[править | править код]
Сближение меридианов – угол между истинным меридианом и вертикальной линией километровой сетки или линией параллельной ей.[1]
Сближение меридианов, указываемое на топографических картах, относится к средней (центральной) точке листа.[4]
Обратная геодезическая задача[править | править код]
Дирекционный угол в декартовых координатах
Дирекционный угол направления на ориентир может быть вычислен путём решения обратной геодезической задачи если известны плоские прямоугольные координаты исходной точки и ориентира.
Решение обратной геодезической задачи выполняется в следующем порядке:
1) вычисляют приращения координат:
2) из решения прямоугольного треугольника определяют румб линии:
.
откуда
3) по знакам приращений координат и по известному румбу линии определяют дирекционный угол линии
| № | Четверть (направление) | связь румба и дирекционного угла | Знак приращения  |
Знак приращения 
|
|---|---|---|---|---|
| 1 | северо-восток | |
+ | + |
| 2 | юго-восток | |
– | + |
| 3 | юго-запад | |
– | – |
| 4 | северо-запад | |
+ | – |
4) определяют горизонтальное проложение (длину линии)
.[5]
Примечания[править | править код]
- ↑ 1 2 А.Ф. Лахин Б.Е. Бызов И.М. Прищепа. Военная топография для курсантов учебных подразделений. — Москва: Военное издательство Министерства Обороны СССР, 1973. — С. 135. — 224 с.
- ↑ А.Ф. Лахин Б.Е. Бызов И.М. Прищепа. Военная топография для курсантов учебных подразделений. — Москва: Военное издательство Министерства Обороны СССР, 1973. — С. 126. — 224 с.
- ↑ 1 2 «Дирекционный угол». Дата обращения: 12 октября 2019. Архивировано 10 января 2022 года.
- ↑ 1.14. ДИРЕКЦИОННЫЕ УГЛЫ И АЗИМУТЫ. Дата обращения: 26 апреля 2020. Архивировано 10 января 2022 года.
- ↑ Обратная геодезическая задача. Дата обращения: 12 октября 2019. Архивировано 10 января 2022 года.
Отвечаю.
Дано:
1. Имеем две точки А и В.
2. Имеем координаты этих точек
ХА, УА, ХВ, УВ.
Найти: дирекционный угол линии АВ (в градусах)
3. Вычисляем разность координат точек
= ХВ-ХА, Дельта У = УВ-УА
4. Делим Дельта У на Дельта Х, получаем тангенс румба.
tg(r)=(УВ-УА) /(ХВ-ХА)
5. Определяем румб (быстренько в поиск со словами “РУМБ ЭТО”!)
r=arctg((УВ-УА) /(ХВ-ХА) (в градусах)
6. И вот мы приступили к нахождению самого дирекционного угла (Снова в поиск со словами “ДИРЕКЦИОННЫЙ УГОЛ ЭТО”).
Вот, слоник уже нашёл:
“Дирекционный угол — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360°, между северным направлением осевого меридиана зоны прямоугольных координат и направлением на ориентир”.
Вот, слоник исправил:
“Дирекционный угол — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360°, между северным направлением осевого меридиана зоны прямоугольных координат и направлением с точки А на точку В”.
7. Процесс нахождения дирекционного угла по известным значениям румба (r), Дельта У (dy) и Дельта Х (dx).
Табличка нахождения дир. угла (Альфа):
Если r=0, и dy=0 –> нет решений. (Точка А совпадает с точкой В)
Если r=0, и dy>0 –>Альфа=0
Если r=0, и dy<0 –>Альфа=180
Если r>0, и dy>0 –>Альфа=r
Если r>0, и dy<0 –>Альфа=180+r
Если r<0, и dy>0 –>Альфа=360+r (r – отрицательна!!!)
Если r<0, и dy<0 –>Альфа=180+r (r – отрицательна!!!)
8. Всё. Успеха в учёбе и точности в расчётах.
(Решишь аналитически – проверь графически)
(Кстати, добрые ответы по остальным двум вопросам уже не нужны?)
