Азимуты
Это направление, измеряемое в градусах по часовой стрелке от севера на азимутальной окружности. Азимутальный круг состоит из 360 градусов. Девяносто градусов соответствует востоку, 180 градусов — югу, 270 градусов — западу, а 360 градусов и 0 градусов — северу.
Слово «азимут» иногда используется как синоним азимута для обозначения направления (показания в градусах) от одного объекта к другому. Такое использование корректно только в первом (СВ) квадранте между 0° и 90°.
Азимуты также можно считывать с юга. Национальная геодезическая служба Национального управления океанических и атмосферных исследований (NOAA) (бывшая Береговая и геодезическая служба США) всегда использует юг в качестве нулевого направления. В пожарной службе дикой природы азимут всегда считывается с северной точки.
Направление ветра
Азимут часто используется для обозначения направления ветра. Традиционно направление ветра указывается как одна из восьми точек компаса (С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ). Однако графики направления ветра и скорости часто дают значение азимута, используя 0° и 360° для севера. Ветры называются по направлению, откуда они дуют. Например, западный ветер дует с запада (или 270°), а юго-восточный ветер дует с юго-востока (135°).
Обратный азимут и обратное визирование
Обратный азимут — это проекция азимута от начала координат до противоположной стороны азимутального круга. В азимутальном круге 360 градусов, поэтому противоположное направление будет 180 градусов (половина 360 градусов) от азимута.
Обратный азимут рассчитывается путем прибавления 180° к азимуту, если азимут меньше 180°, или вычитания 180° из азимута, если он больше 180°. Например, если азимут равен 320°, обратный азимут будет 320° – 180° = 140°. Если азимут равен 30°, обратный азимут будет равен 180° + 30° = 210°.
Обратное прицеливание — это метод прицеливания, в котором используется отсчет азимута, снятый в обратном направлении.
Компас – это инструмент, используемый для навигации и ориентации. Азимутальный компас градуирован/отмечен полным кругом в 360 градусов, который называется азимутальным кругом. Компоненты компаса включают магнитную стрелку, которая всегда указывает на магнитный север, градуированную окружность для откладывания углов от истинного севера и линию визирования для продолжения линии визирования при следовании курсу направления.
Условные знаки
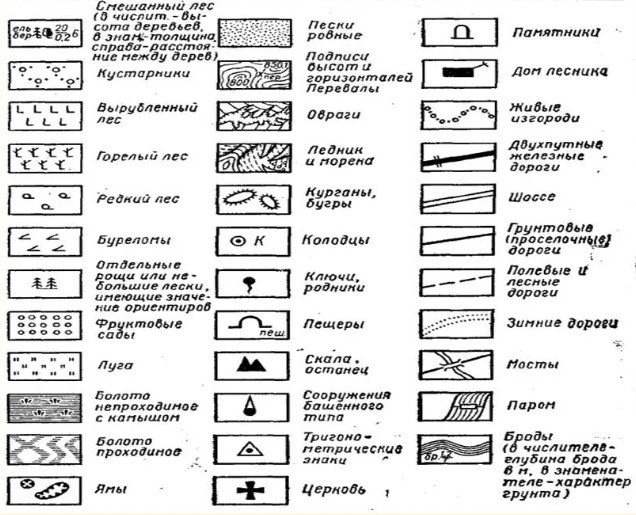
Дирекционные углы и румбы
Дирекционные углы и румбы используются для ориентирования линий.
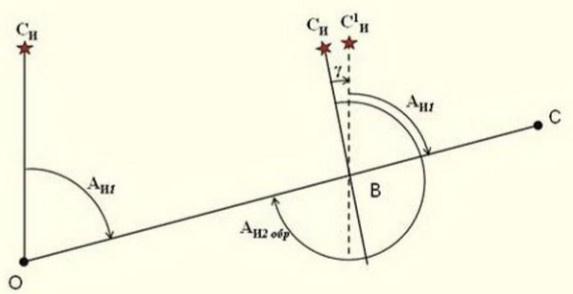
Дирекционным углом (α) линии называют угол, отсчитанный по ходу часовой стрелки от северного направления вертикальной линии километровой сетки (осевого меридиана зоны) до направления заданной линии. Пределы изменения дирекционного угла от 0º до 360º.
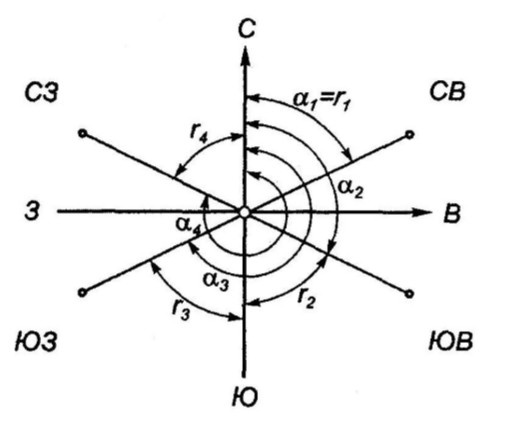
Это острый угол от ближайшего направления меридиана (северного или южного) до направления ориентирной линии. Пределы изменения румба от 0º до 90º.
Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблице ниже.
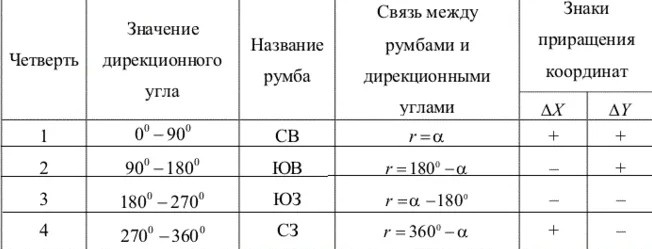
Пример перевода дирекционных углов в румбы
- если дирекционный угол α равен 42°15′55″, тогда согласно таблице румб вычисляется по формуле r=α=42°15′55″, а название румба будет СВ;
- если дирекционный угол α равен 100°45′11″, тогда согласно таблице румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ;
- если дирекционный угол α равен 210°17′42″, тогда согласно таблице румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ;
- если дирекционный угол α равен 335°28′32″, тогда согласно таблице румб вычисляется по формуле r=360°-α=360°-335°28′32″=24°31′28″, а название румба будет СЗ.
румбом
называется острый горизонтальный угол,
отсчитываемый от ближайшего направления
осевого меридиана (северного или южного)
до данной линии. Румбы обозначают буквой
r с индексом, указывающим четверть, в
которой находится румб.
Зависимость
между дирекционными углами и румбами
определяется для четвертей по следующим
формулам:
I
четверть (СВ) r = α
II
четверть (ЮВ) r = 180° – α
III
четверть (ЮЗ) r = α – 180°
IV
четверть (СЗ) r = 360° – α
Румб
в точке М направления ВС называется
прямым, а противоположного направления
СВ – обратным. Прямой и обратный румб
в одной и той же точке данной линии равны
по численному значению, но имеют индексы
противоположных четвертей.
19. Прямая геодезическая задача
В
геодезии часто приходится передавать
координаты с одной точки на другую.
Например, зная исходные координаты
точки А (рис.23), горизонтальное расстояние
SAB от неё до точки В и направление линии,
соединяющей обе точки (дирекционный
угол αAB или румб rAB), можно определить
координаты точки В. В такой постановке
передача координат называется прямой
геодезической задачей.
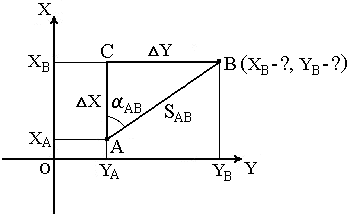
Для
точек, расположенных на сфероиде, решение
данной задачи представляет значительные
трудности. Для точек на плоскости она
решается следующим образом.
Дано:
Точка А( XA, YA ), SAB и αAB. Найти: точку В( XB,
YB ).
Непосредственно
из рисунка имеем:
ΔX
= XB – XA ; ΔY = YB – YA .
Разности
ΔX и ΔY координат точек последующей и
предыдущей называются приращениями
координат. Они представляют собой
проекции отрезка АВ на соответствующие
оси координат. Их значения находим из
прямоугольного прямоугольника АВС:
ΔX
= SAB · cos αAB ;ΔY = SAB · sin αAB .
Так
как в этих формулах SAB всегда число
положительное, то знаки приращений
координат ΔX и ΔY зависят от знаков cos
αAB и sin αAB.
При
помощи румба приращения координат
вычисляют по формулам:
ΔX
= SAB · cos rAB ;ΔY
= SAB · sin rAB .
Знаки
приращениям дают в зависимости от
названия румба. Вычислив приращения
координат, находим искомые координаты
другой точки:
XB
= XA + ΔX ; YB = YA + ΔY .
Таким
образом можно найти координаты любого
числа точек по правилу: координаты
последующей точки равны координатам
предыдущей точки плюс соответствующие
приращения.
Контроль
вычислений координат выполняют по
формуле
20. Обратная геодезическая задача
Обратная
геодезическая задача – это вычисление
дирекционного угла α и длины S линии,
соединяющей два пункта с известными
координатами X1, Y1 и X2, Y2
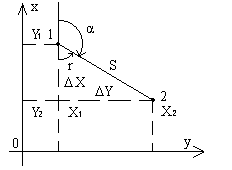
Построим
на отрезке 1-2 как на гипотенузе
прямоугольный треугольник с катетами,
параллельными осям координат. В этом
треугольнике гипотенуза равна S, катеты
равны приращениям координат точек 1 и
2 ( ΔX = X2 – X1, ΔY = Y2 – Y1 ), а один из острых
углов равен румбу r линии 1-2.
Если
Δ X 00 и Δ Y 00, то решаем треугольник по
известным формулам:
Для
данного рисунка направление линии 1-2
находится во второй четверти, поэтому
на основании (1.22) находим:
Общий
порядок нахождения дирекционного угла
линии 1-2 включает две операции:
*
определение номера четверти по знакам
приращений координат Δ>X и ΔY (рис.1.4-а),
*
вычисление α по формулам связи (1.22) в
соответствии с номером четверти.Контролем
правильности вычислений является
выполнение равенства:
Контроль:
d . cos α + XA = XB, d . sin α + YB = YB.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2016 года; проверки требуют 106 правок.
6-градусные зоны В Проекции Гаусса — Крюгера
1-я четверть n-градусной зоны и линии параллельный осевому меридиану
Дирекционный угол — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением осевого меридиана зоны прямоугольных координат и направлением на ориентир. Дирекционные углы направлений измеряются преимущественно по карте.[1]
Вся земная поверхность, будучи шарообразной, не может быть перенесена на плоскость без разрывов и искажений. Поэтому её разделили на равные части ограниченные меридианами с разностью долгот в n градусов, имеющие наименование n-градусной координатной зоны. В каждой такой зоне за вертикальную ось координат (ось Х) принят осевой меридиан. Горизонтальная ось Y дополняет систему до правой и служит во всех зонах линией экватора. Пересечение осей в каждой зоне принимается за начало координат. Значение координат Х положительными считается к северу от линии экватора (OY). Угол по ходу часовой стрелки от 0° до 360° между северным направлением оси Х (вертикальной линией километровой сетки) и направлением на предмет является Дирекционным углом.[2]
Дирекционные углы применяются при выполнении засечек или прокладке полигонометрического хода путём передачи угловых измерений от направления с известным дирекционным углом к искомым.
[3]
Не стоит путать дирекционный угол и пеленг.
Взаимосвязь Дирекционного угла с прочими углами ориентирования[править | править код]
Шкалы географических координат и километровая сетка на карте масштабом 1:25000. Сопоставление угловых и прямоугольных координат
Дирекционные углы направлений могут определяться геодезическим, магнитным, астрономическим и гироскопическим способами, а также методами космической геодезии.
Магнитный азимут[править | править код]
Магнитный способ заключается в определении с помощью магнитной стрелки компаса (буссоли) и по данным о склонении магнитной стрелки.[3]
Приближенные значения дирекционных углов направлений (
) с точностью порядка 10-25 угловых минут могут быть вычислены из значения магнитного азимута направления (
), который определен с помощью компаса или ориентир-буссоли, которая входит в комплект дополнительного оборудования теодолитов и тахеометров. Ориентир-буссоль предназначена для определения магнитных азимутов направлений (с точностью 1-60 угловых секунд). Для перехода от магнитного азимута к дирекционному углу необходимо знать Склонение магнитной стрелки (
), которое определяется, как правило, на исходном геодезическом пункте в районе выполнения работ и указана на топографических картах.
Географический азимут[править | править код]
Географический азимут – является дирекционным углом.
Геодезический румб[править | править код]
Связь между Геодезический румбом и дирекционным углом устанавливается по формулам:
I Четверть – 
II Четверть 
III Четверть 
IV четверть 
Навигационный румб[править | править код]
Связь между Навигационный и дирекционным углом устанавливается по формуле:
– уход магнитной стрелки влево относительно норда
+ уход магнитной стрелки вправо относительно норда
Сближение меридианов[править | править код]
Сближение меридианов – угол между истинным меридианом и вертикальной линией километровой сетки или линией параллельной ей.[1]
Сближение меридианов, указываемое на топографических картах, относится к средней (центральной) точке листа.[4]
Обратная геодезическая задача[править | править код]
Дирекционный угол в декартовых координатах
Дирекционный угол направления на ориентир может быть вычислен путём решения обратной геодезической задачи если известны плоские прямоугольные координаты исходной точки и ориентира.
Решение обратной геодезической задачи выполняется в следующем порядке:
1) вычисляют приращения координат:
2) из решения прямоугольного треугольника определяют румб линии:
.
откуда
3) по знакам приращений координат и по известному румбу линии определяют дирекционный угол линии
| № | Четверть (направление) | связь румба и дирекционного угла | Знак приращения  |
Знак приращения 
|
|---|---|---|---|---|
| 1 | северо-восток | |
+ | + |
| 2 | юго-восток | |
– | + |
| 3 | юго-запад | |
– | – |
| 4 | северо-запад | |
+ | – |
4) определяют горизонтальное проложение (длину линии)
.[5]
Примечания[править | править код]
- ↑ 1 2 А.Ф. Лахин Б.Е. Бызов И.М. Прищепа. Военная топография для курсантов учебных подразделений. — Москва: Военное издательство Министерства Обороны СССР, 1973. — С. 135. — 224 с.
- ↑ А.Ф. Лахин Б.Е. Бызов И.М. Прищепа. Военная топография для курсантов учебных подразделений. — Москва: Военное издательство Министерства Обороны СССР, 1973. — С. 126. — 224 с.
- ↑ 1 2 «Дирекционный угол». Дата обращения: 12 октября 2019. Архивировано 10 января 2022 года.
- ↑ 1.14. ДИРЕКЦИОННЫЕ УГЛЫ И АЗИМУТЫ. Дата обращения: 26 апреля 2020. Архивировано 10 января 2022 года.
- ↑ Обратная геодезическая задача. Дата обращения: 12 октября 2019. Архивировано 10 января 2022 года.
В системе прямоугольных координат для ориентирования линий применяются ДИРЕКЦИОННЫЙ УГОЛ и РУМБ.
Дирекционным углом называют горизонтальный угол,
отсчитываемый от положительного направления линии параллельной оси абсцисс,
по ходу часовой стрелки до направления ориентируемой линии.
Изменяется в пределах от 0 до 360 градусов.
Дирекционный угол в разных точках прямой одинаков.
На местности дирекционный угол не измеряют! Его значение вычисляют.
Различают прямой и обратный дирекционные углы.
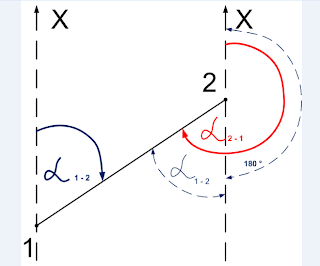
РУМБ – это острый горизонтальный угол, отсчитываемый от ближайшего северного или южного направления до направления ориентируемой линии .
Румб изменяется от 0 до 90 градусов.
К названию румба добавляется номер четверти, в которой он расположен.
Обратный румб отличается от прямого только противоположной стороной света .
В ПЕРВОЙ ЧЕТВЕРТИ ДИРЕКЦИОННЫЙ УГОЛ РАВЕН РУМБУ.
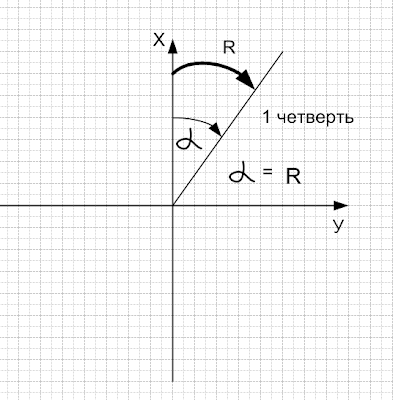
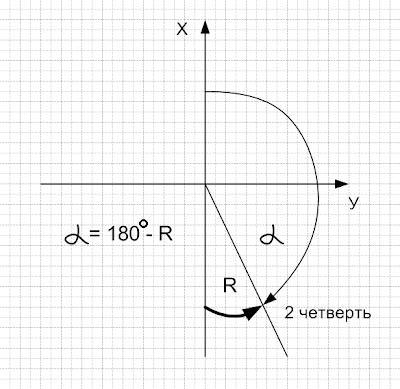
ВО ВТОРОЙ ЧЕТВЕРТИ
ДИРЕКЦИОННЫЙ УГОЛ РАВЕН 180 ГРАДУСОВ МИНУС РУМБ
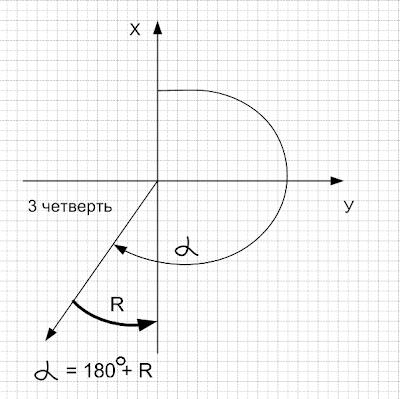
В ТРЕТЬЕЙ ЧЕТВЕРТИ
ДИРЕКЦИОННЫЙ УГОЛ РАВЕН 180 ГРАДУСОВ ПЛЮС РУМБ
В ЧЕТВЁРТОЙ ЧЕТВЕРТИ
ДИРЕКЦИОННЫЙ УГОЛ РАВЕН 360 ГРАДУСОВ МИНУС РУМБ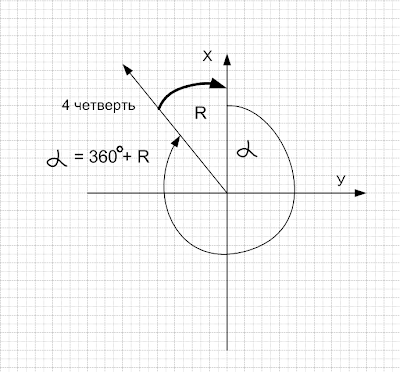
ВСЕГДА ПОМНИМ, ЧТО В ГЕОДЕЗИИ ОСЬ Х (ОСЬ АБЦИСС) ПОКАЗЫВАЕТ НА СЕВЕР (В ВЕРХ).
Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.
Решение обратной геодезической задачи онлайн
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB
Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.
Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.
Сначала находим приращения координат:
ΔX = XB – XA ;
ΔY = YB – YA .
Величину угла rAB определяем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
