Как найти дисконтированную стоимость по периодам

Как найти дисконтированную стоимость по периодам

Метод дисконтирования основан на известном экономическом законе, который заключается в убывающей стоимости денег. Деньги со временем обесцениваются — это заметно даже тем, кто не знаком с экономической теорией. При растущих ценах реальная стоимость денег уменьшается, то есть на условные 1000 руб. завтра мы сможем купить меньше, чем сегодня, и меньше, чем вчера. Чтобы ответить на вопрос, сколько в будущем будут стоить сегодняшние 1000 руб., используется метод дисконтирования денежных потоков. Пример расчета и наглядное объяснение данного метода вы найдете в статье ниже.

Расчет дисконтированного денежного потока

Стоимость денег может изменяться не только под влиянием инфляции, но и за счет других факторов. Например, деньги в форме депозита в банке могут принести прибыль, а при выдаче денег в кредит всегда существует риск недополучения предполагаемой возвратной суммы. Точка отсчета в методе дисконтирования — настоящий момент. Именно на текущую дату определяется стоимость будущих денежных потоков.

Дисконтирование денежных потоков— это приведение размера денежных средств, полученных в разные интервалы времени в соответствие с их реальной стоимостью на текущий момент. Метод применяется при оценке бизнеса и анализе экономической эффективности инвестиционных проектов, расчете их окупаемости и составлении бизнес-планов. Рассчитывая экономическую целесообразность будущего бизнес-проекта, инвестор приводит в соответствие планируемый объем будущих денежных потоков к их текущей реальной стоимости.

Формулы сложных процентов и дисконтирования

Смысл операции дисконтирования легко объяснить на небольшом примере. Например, в наличии сумма S0 = 1000 руб. Если положить эту сумму в банк под 7% годовых с ежегодной капитализацией процентов, т.е. зачислением их во вклад в конце года, мы получим через год:

S1 =1000 + 0,07 х 1000 = (1 + 0,07) х 1000 = 1070 руб.

Через 2 года: S2 = (1 + 0,07) х (1 + 0,07) х 1000 = (1+ 0,07)2 х 1000 = 1144,90 руб.

Через 3 года: S3 = (1+0,07)3 х 1000 = 1225,04 руб.

Через n-лет: Sn = (1+0,07)n х 1000, и таким образом формула сложных процентов выглядит так:

Sn = (1+P)n х S0, где

Sn — сумма денег через n-периодов начисления процентов;

S0 — первоначальная сумма денег;

P — процентная ставка по депозиту за период.

Подведем итог: при размещении денег на депозите сумма в размере 1000 руб., которая имеется в наличии сейчас, будет равняться по стоимости 1070 рублям, полученным через 1 год, и сумме 1225,04 руб., выплаченной через 3 года и т. д.

Расчет дисконтированного денежного потока – задание, обратное предыдущему: необходимо вычислить сумму S0 на текущий момент времени, равную по стоимости сумме Snчерез n-количество лет. Другими словами,величина Sn нам известна, нужно рассчитать S0.

Формула дисконтирования после простых математических преобразований расчета сложных процентов будет выглядеть так:

S0 = Sn / (1+P)n.

Величина P в этом расчете не процентная ставка, а ставка дисконтирования.

S0 — это продисконтированный денежный поток;

Sn — денежный поток каждого расчетного периода. Число n в формуле обозначает количество расчетных периодов, как правило, расчетным периодом в экономических расчетах считают год, иногда квартал или месяц.

Таким образом, если вернуться к предыдущему примеру, при ставке дисконтирования 7% деньги в сумме 1070 руб., выплаченные через 1 год, будут равняться 1000 руб. в настоящем: 1070 / (1+ 0,07) = 1000.

Инструменты дисконтирования: денежные потоки и ставка

В начале расчетов денежные потоки группируют в разрезе некоторых временных интервалов: год, квартал, месяц, а затем суммируют. Полученные величины могут быть с плюсом (поступления больше оттоков) или с минусом, убыточными (отток превышает сумму поступлений). В качестве денежного потока в расчетах могут считать:

  • чистый доход, равный поступившим доходам за вычетом расходов;

  • прибыль, рассчитываемая до исчисления налогов;

  • чистый поток наличности, из которого исключаются текущие затраты на содержание и реконструкцию объекта.

Вычисление ставки дисконтирования — наиболее ответственный момент в расчетах. В самом простом варианте, когда инвестор планирует разместить деньги на депозите, защитив их от инфляции, в качестве основы для расчета ставки применяют прогнозируемый индекс инфляции. Если кроме сбережения финансов планируется еще и получение дополнительной прибыли, то к ставке инфляции добавляется желаемый процент дохода. При инвестициях, особенно долгосрочных, необходимо учитывать не только инфляцию и норму ожидаемой прибыли, но различные сопутствующие риски. Поэтому в ставку дисконтирования закладываются еще и так называемые премии за риск, а при пользовании заемными средствами для реализации инвестиционного проекта к ставке добавляют еще процент по банковским кредитам, выпуску облигаций и т. п.

Чаще всего при анализе окупаемости дисконтная ставка складывается из безрисковой базовой доходности, приравненной к ключевой ставке ЦБ РФ или средневзвешенному проценту по банковским депозитам с добавлением премии за риск.

Дисконтирование денежных потоков: пример расчета

Проведем расчет дисконтированных денежных потоков для инвестиционных вложений сроком на 3 года. В нашем примере дисконтная ставка равна 15%, из них 8% — средневзвешенная ставка банковских депозитов и 7% — премия за риск. Период дисконтирования равен 1 году.

1. Выпишем для каждого годового периода ожидаемую сумму дохода и расходов в рублях. Будем считать, что расходы каждый год будут неизменными, а размер поступлений будет меняться.

2. Рассчитаем разность между доходами и расходами на каждый год.

Таблица расчета:

Период

Доходы

Расходы

Чистый доход

1 год

80 000

90 000

-10 000

2 год

120 000

90 000

+30 000

3 год

150 000

90 000

+ 60 000

3. Приводим финансовые потоки в соответствие к текущему моменту, используя ставку дисконтирования 15%. Применяем коэффициент дисконтирования (1 + 0,15)n, дисконтирующий каждый поток, где n — число каждого года, для которого делаем расчет. Итак:

1 год: -10 000 / (1 + 0,15) = -8 695,65 руб.

2 год: +30 000 / (1 + 0,15)2 = 22 727,27 руб.

3 год: +60 000 / (1 + 0,15)3 = 39 473,68 руб.

4. Полученные суммы складываем:

-8 695,65 + 22 727,27 + 39 473,68 = 53 505,30 руб.

Сумма 53 505,30 – это дисконтированный денежный поток. Положительная величина свидетельствует о привлекательности данного проекта для инвесторов и возможности последующего анализа его перспективности.

Источник

Одним из важнейших критериев оценки инвестиционного проекта является коэффициент дисконтирования. Качественное бизнес-планирование предполагает обязательный учет изменения стоимости денег со временем, поэтому все будущие денежные потоки следует приводить к текущему состоянию. Остановимся подробнее на том, что такое коэффициент дисконта и как определить его величину.

Содержание статьи

  • Понятие коэффициента дисконтирования и его значение
  • Способ определения величины показателя
  • Примеры вычисления потоков денег с использованием фактора дисконта
  • Некоторые особенности практических расчетов фактора приведения

Понятие коэффициента дисконтирования и его значение

Понятие коэффициента дисконтированияКоэффициент дисконтирования денежных потоков – это цифровой показатель, используя который можно понять, сколько денег удастся получить через определенное время с учетом временного фактора и возможного риска. Таким образом, производится приведение потоков денег в будущем к состоянию на день анализа.

В бизнес-проектировании “деньги сейчас” всегда предпочтительнее, чем “деньги потом”, поскольку их можно вложить в другое дело и получить доход или разместить на банковском депозите и получать фиксированный процент. Следовательно, перед вложением инвестор должен быть уверен, что в течение жизненного цикла проекта он не только не потеряет от удешевления денег, но и сможет получить прибыль.

Интервал времени, на протяжении которого реализуется начинание и приносит прибыль участникам, устанавливается заранее. Он, как правило, определяется по нормативным срокам применения установленного оборудования, после чего технические возможности производства продукции исчерпываются. От правильного определения временных рамок начинания во многом зависит объективность вычислений.

Значение коэффициента дисконтирования используется в разных ситуациях:

  • оценка эффективности экономической деятельности какой-либо фирмы;
  • расчет эффективности инвестиционного проекта;
  • рассмотрение альтернативных вариантов вложения средств как между разными инициативами, так и внутри одного предприятия (выбор наиболее перспективного пути развития);
  • многосторонние расчеты и кредитование.

Этот показатель фактически устанавливает некий норматив издержек или поступления капитала при вложении его в другое начинание. Иными словами, коэффициент (или фактор) дает возможность определить размер процента, на который следует множить ожидаемые доходы для того, чтобы выйти на конкретную сумму применительно к сегодняшнему состоянию.

Способ определения величины показателя

Рассмотрим подробнее, как рассчитать коэффициент дисконтирования. Обычно речь идет о многошаговом расчете перспективности и экономической эффективности инвестиционного начинания, поэтому фактор дисконтирования приводит объем потока на n-м шаге к моменту приведения.

Общая формула дисконтирования потока денег имеет такой вид:

PV = FV * 1/(1+R)n

где:

  • PV – приведенная стоимость;
  • FV – будущая стоимость.

В этой формуле выделяется компонент, определяющий величину фактора приведения. Собственно, формула расчета коэффициента дисконтирования выглядит так:

КД = 1/(1+R)n

в которой:

  • R – установленное значение нормы дисконта;
  • n – количество периодов (шагов), представляющее собой число лет (месяцев) от будущего до текущего момента.

Получившийся показатель всегда имеет значение меньше единицы. Он показывает стоимость одной инвестированной денежной единицы (рубля, евро, доллара) через определенное время при соответствии условий тем, которые приняты для вычисления.

Важнейшей составной частью для расчета коэффициента является ставка дисконтирования, которую еще называют нормой дисконта. Для ее определений существует целый ряд методик, основанных на различных принципах:

  • дивидендный метод (модель Гордона);
  • стоимость капитальных активов предприятия (модель CAPM и ее многочисленные модификации);
  • наличие заемных и собственных средств (модель WACC);
  • метод значений рентабельности капитала (ROE, ROA, ROACE, ROCE);
  • метод вычисления рисковых премий (кумулятивный);
  • экспертный метод, основанный на субъективных прогнозах специалистов.

модель ГордонаЗа норму дисконта можно принимать темпы инфляционных процессов, стоимость долгосрочных депозитов или кредитов, размер ставки рефинансирования Центробанка и т.д. В любом случае, каков будет этот критерий, решает на свой страх и риск инвестор. Если норма дисконта установлена неверно или в ней не учтены все основные риски, то и фактор приведения будет некорректным. Это даст инвестору неверный прогноз, который может привести к убыткам.

Другая составляющая формулы – это жизненный цикл начинания, то есть количество рассматриваемых периодов, в течение которых проект будет генерировать денежные потоки. Чем точнее, установлены эти две вводные, тем более точным будет конечный результат.

Примеры вычисления потоков денег с использованием фактора дисконта

Рассмотрим пример расчета. Бизнесмен вкладывает в новый шестилетний проект 800 тысяч рублей. Согласно с представленным инициатором бизнес-планом, через 6 лет он сможет единоразовым платежом получить 1,5 миллиона рублей. Кумулятивным способом определена ставка дисконтирования 12%, при этом процент нормы дисконта записывается при подсчете в виде части от единицы (0,12). Теперь, используя стандартную формулу, можно посчитать величину фактора:

Kd = 1 / (1 + 0,12) 6

Kd = 1 / 1,9738

Kd = 0,5066

Мы получили коэффициент приведения в размере 0,5066. После этого по формуле дисконтирования рассчитываются показатели стоимости приведенного денежного потока:

PV = FV * 1/(1+R)n. 

PV = 1500000 * 0,5066

PV = 759900

Из полученного результата можно сделать неутешительный для инвестора вывод, что при таких стартовых условиях ему не следует ожидать не только прибыли, но и даже простого возврата вложенных денег. Следовательно, от такого предложения нужно отказаться или же предложить изменить основные условия проекта, если это приемлемо (сократить срок реализации или уменьшить норму дисконта).

Предположим, что норма дисконта в нашем примере снижена до 10%. В таком случае значение коэффициента составит 0,5645, а приведенный поток денег возрастет до 846750 рублей, что сделает проект прибыльным. Аналогичная ситуация возникает и в случае сокращения срока внедрения до 5 лет при ставке 12%: фактор будет 0,5674, а поток – 851100 рублей.

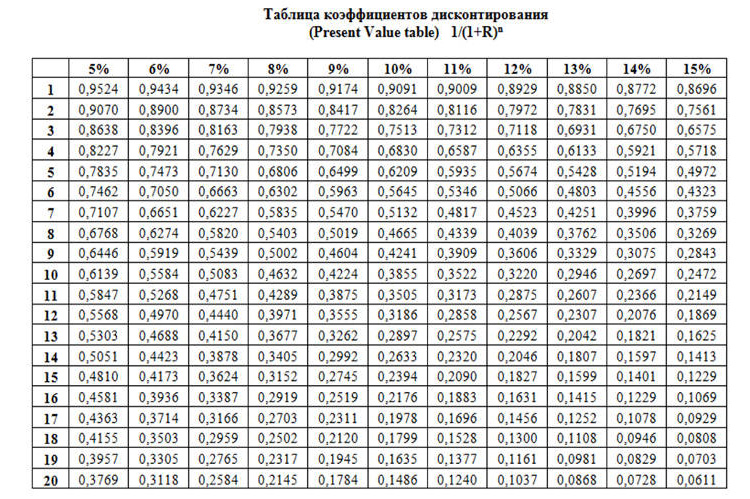
Следует отметить, что для того, чтобы определить коэффициент дисконтирования, нет необходимости каждый раз погружаться в математические формулы. Для упрощения этого задания разработана и широко применяется на практике таблица коэффициентов дисконтирования. Она построена по стандартной схеме, как таблицы Пифагора или Брадиса, то есть на одной оси указаны размеры процентных ставок, на другой – временные отрезки. Для нахождения нужного показателя достаточно найти ячейку, где они пересекаются, в ней содержится величина коэффициента с точностью до десятитысячных (до четвертого знака после запятой).Таблица коэффициентов дисконтирования

Все приведенные выше значения коэффициентов, взяты из этой таблицы. Это значительно ускоряет расчеты и дает возможность без лишних усилий просчитывать альтернативные варианты развития событий.

Мы рассматривали задачу, в которой предусматривалась выплата денег одним платежом после окончания проекта. На практике, гораздо чаще встречаются ситуации, когда выплаты производятся ежегодно. Тогда для корректности расчетов необходимо находить коэффициент приведения для каждого года отдельно. К примеру, свои полтора миллиона наш инвестор получит за 6 лет жизненного цикла инициативы при норме дисконта 10% равными частями по 250 тысяч рублей в год (т.е. как аннуитет):

Применяя формулу годовых расчетов, можно находить коэффициенты отдельно по каждому периоду, а затем просуммировать их:

CF1 CF2 CFN
NPV = —– + —— +…+ ——
(1+R) (1+R)2 (1+R)6

PV = 227272 + 206611 + 187828 + 170765 + 155279 + 141083 = 1088838 рублей.

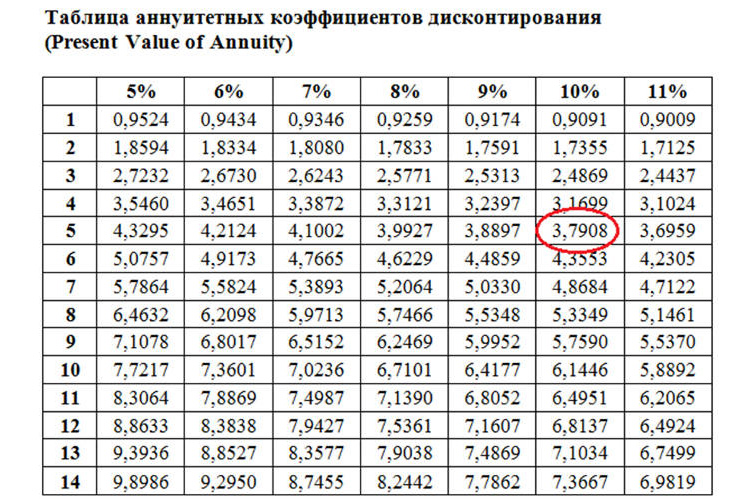
Если же использовать таблицу коэффициентов аннуитетных платежей, то достаточно будет размер среднегодового платежа умножить на фактор, указанный в нужной ячейке таблицы (в данном случае это 4,3553).Таблица аннуитентных коэффициентов дисконтирования

PV = 250000 * 4,3553 = 1088825 рублей

Таким образом, мы видим, что показатель, найденный по формуле, практически аналогичен величине, определенной при помощи таблиц (1088838 против 1088825).

Некоторые особенности практических расчетов фактора приведения

В заключение хотелось бы остановиться еще на нескольких моментах, связанных с приведением денежных потоков, о которых спрашивают пользователи Интернета. В частности, возникает вопрос, как вычислять фактор, когда шаг задается в разных единицах, например годах и месяцах, и различаются ли формулы при таких расчетах.

При периоде дисконтирования, равном одному месяцу, коэффициент высчитывается по такой формуле:

1 / (1 + R) в степени (Месяц – 1) / 12,

где:

  • R – норма дисконта;
  • Месяц – номер порядковый месяца проекта.

При годовом периоде приведения применяется такой механизм расчета:

1 / (1 + R) в степени Год – 1,

где:

  • Год – номер порядковый года жизненного цикла начинания.

Если же период считается поквартально, то для каждого месяца квартала принимается во внимание показатель, равный последнему месяцу в квартале, то есть для 1, 2 и 3 месяца берется показатель 3 месяца и т.д.

Также на форумах обсуждают ситуацию, когда контролирующие органы иногда требуют считать коэффициент приведения по формуле КД = 1/(1+R)^(n-0,5) вместо стандартной КД = 1/(1+R)^n.

Такой подход называется моделью среднегодового дисконтирования.Здесь дисконтирование проводится по состоянию на середину календарного года (или периода приведения), а не на его начало или конец.

Среднепериодическое дисконтирование применяется в случаях, когда идет постоянный равномерный приток денег (например, от работы промышленного предприятия). Хотя среди специалистов мнения о целесообразности такого метода расчета расходятся.

Коэффициент дисконта, благодаря своей гибкости широко используется экономистами и финансистами. Он показывает перспективу и потенциальную доходность отдельного проекта во временном отрезке. При этом, у этого финансового инструмента есть серьезный недостаток: он хорошо работает в государствах со стабильными рынками и налаженными рыночными механизмами. Применение его в странах, для которых характерна переходная экономическая модель, грозит существенными неточностями, поскольку адекватно просчитать многие риски для нахождения нормы дисконта в таких условиях очень трудно.

Источник

Дисконтированная (приведённая, текущая) стоимость — оценка стоимости (текущий денежный эквивалент) будущего потока платежей исходя из различной стоимости денег, полученных в разные моменты времени (концепция временно́й ценности денег). Денежная сумма, полученная сегодня, обычно имеет более высокую стоимость, чем та же сумма, полученная в будущем. Это связано с тем, что деньги, полученные сегодня, могут принести в будущем доход после их инвестирования. Кроме того, деньги полученные в будущем в условиях инфляции обесцениваются (на ту же сумму в будущем можно приобрести меньшее количество товаров и услуг). Также есть другие факторы, снижающие стоимость будущих платежей. Неравноценность разновременных денежных сумм численно выражается в ставке дисконтирования.

Дисконтированная стоимость некоторой будущей суммы X равна денежной сумме, при инвестировании которой сейчас (с доходностью, равной ставке дисконтирования), в будущем (в тот же момент времени) будет получена сумма X . Дисконтированная стоимость потока платежей равна сумме дисконтированных стоимостей отдельных платежей, входящих в этот поток. Она фактически равна дисконтированной величине будущей стоимости денежного потока (сумма, которая будет получена в будущем, если денежный поток инвестировать в моменты получения платежей под ставку дисконтирования).

Дисконтированная стоимость широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объём финансовых вложений готов сделать инвестор для получения данного денежного потока. Дисконтированная стоимость будущего потока платежей является функцией ставки дисконтирования, которая может определяться в зависимости от:

  • доходности альтернативных вложений;
  • стоимости привлечения (заимствования) средств;
  • инфляции;
  • срока, через который ожидается будущий поток платежей;
  • риска, связанного с данным будущим потоком платежей;
  • других факторов.

Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.

Практическое объяснение[править | править код]

Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену вследствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб., которые будут получены через пять лет.

Наращение процентов и дисконтирование[править | править код]

Пусть некоторая денежная сумма PV вкладывается под ставку i за единицу времени (день, месяц, квартал, год). Предполагается, что проценты начисляются и капитализируются в каждую единицу времени и фактически реинвестируются. Тогда в будущий момент времени t будет получена сумма FV_{t}, рассчитанная по формуле сложных процентов:

{displaystyle FV_{t}=PV(1+i)^{t}}

Соответственно, если дана денежная сумма FV_{t} на некоторый будущий момент времени t, можно рассчитать сумму PV, которую нужно вложить под ставку i, чтобы получить FV_{t} к этому моменту, следующим образом:

{displaystyle PV=FV_{t}(1+i)^{-t},={frac {FV_{t}}{(1+i)^{t}}}}

Величину PV называют дисконтированной (приведённой, текущей) стоимостью будущей суммы FV_{t}, а ставку i — ставкой дисконтирования. Саму операцию нахождения текущей стоимости будущей суммы называют дисконтированием.

В общем случае сумма может быть приведена к любому моменту времени (не только к текущему):

{displaystyle PV_{t_{0}}={frac {FV_{t}}{(1+i)^{t-t_{0}}}}}

Приведение разновременных сумм к одному и тому же моменту времени делает их сопоставимыми (равноценными) с точки зрения концепции временно́й ценности денег. Предполагается, что существует возможность вложить любую сумму в любой момент времени в некоторый инструмент (например, банковский депозит) с доходностью i. Природа инструмента несущественна, имеет значение только доходность при сопоставимом риске. В случае, если в качестве i используется инфляция — это вложения в дорожающие товары и услуги. В качестве i может выступать стоимость привлечения (заимствования) денег.

Пример[править | править код]

Если через 1 год ожидается сумма 121 рубль, то при ставке дисконтирования 10 % годовых дисконтированная стоимость будет равна {displaystyle 121/(1+0{,}1)=110} рублей. Если эта же сумма ожидается только через два года, то дисконтированная стоимость равна {displaystyle 121/(1+0{,}1)^{2}=121/1{,}21=100} рублей.

В табличных процессорах в состав финансовых функций входит функция для вычисления дисконтированной стоимости. В OpenOffice.org Calc для вычисления дисконтированной стоимости различных видов платежей применяется функция PV.

Дисконтированная стоимость денежных потоков[править | править код]

Денежные потоки[править | править код]

Денежным потоком называют распределённое во времени движение денежных средств. Во многих случаях (депозиты, кредиты, ценные бумаги и др.) денежный поток представляет собой упорядоченную по времени совокупность денежных сумм (платежей) — это так называемый дискретный денежный поток или поток платежей. Таким образом, поток платежей {displaystyle CF=(CF_{1},CF_{2},....,CF_{n})}, где {displaystyle CF_{k}} — платёж, осуществляемый в момент времени t_k, {displaystyle k=1..n}. При этом формально n может быть также и бесконечным (бесконечный поток платежей). Если платежи осуществляются через равные промежутки времени, то иногда такой поток платежей называют финансовой рентой. Рента с постоянной величиной платежа называется аннуитетом (в некоторых источниках финансовая рента и аннуитет — эквивалентные понятия).

В некоторых случаях частота платежей может быть настолько большой, что денежный поток можно считать непрерывным. В частности, это имеет место для денежных потоков от обычной операционной деятельности компаний, потоков от инвестиционных проектов и т. д. Формально для непрерывных потоков можно ввести функцию плотности потока {displaystyle c(t)}. Однако, на практике непрерывное время заменяется дискретным. А именно анализируемый период разбивается на равные периоды (месяц, квартал, год) и каждый период получает последовательный номер (это и есть дискретное время). Тогда денежный поток за каждый такой период {displaystyle CF_{t}} является фактически платежом в дискретный момент времени, соответствующий этому периоду. Таким образом непрерывный поток сводится, точнее моделируется как дискретный поток (поток платежей), описанный выше. Часто это интерпретируется также как платежи, осуществляемые в конце соответствующего периода — это так называемый поток постнумерандо. В некоторых случаях потоки рассматривают как платежи в начале каждого периода — поток пренумерандо.

Таким образом, можно считать, что денежный поток CF задаётся всегда упорядоченной совокупностью денежных сумм {displaystyle CF_{t}} — элементов денежного потока (платежей).

Дисконтированная стоимость потока платежей[править | править код]

Дисконтированная стоимость потока платежей {displaystyle CF=(CF_{1},CF_{2},....,CF_{n})}, где {displaystyle CF_{k}} — платёж, осуществляемый в момент времени t_k, {displaystyle k=1..n}, равна сумме дисконтированных стоимостей каждого из составляющих потока:

{displaystyle PV=sum _{k=1}^{n}{{frac {CF_{k}}{(1+i)^{t_{k}}}},}}

Вывод формулы

Поток платежей разобьём на первый {displaystyle CF_{1}} и остальной {displaystyle (CF_{2},CF_{3},....)}. Обозначим приведённую к моменту первой выплаты стоимость остаточного денежного поток {displaystyle PV_{1}^{*}}. Суммы {displaystyle CF_{1}} и {displaystyle PV_{1}^{*}} относятся к одному моменту времени и их можно привести к текущему моменту делением на {displaystyle (1+i)^{t_{1}}}

{displaystyle PV_{0}={frac {CF_{1}}{(1+i)^{t_{1}}}}+{frac {PV_{1}^{*}}{(1+i)^{t_{1}}}}}

Аналогичным образом можно разделить остаточный поток на платёж {displaystyle CF_{2}} и оставшийся после t_{2} поток и получим

{displaystyle PV_{1}^{*}={frac {CF_{2}}{(1+i)^{t_{2}-t_{1}}}}+{frac {PV_{2}^{*}}{(1+i)^{t_{2}-t_{1}}}}}

Подставив это в первую формулу получим

{displaystyle PV_{0}={frac {CF_{1}}{(1+i)^{t_{1}}}}+{frac {CF_{2}}{(1+i)^{t_{2}}}}+{frac {PV_{2}^{*}}{(1+i)^{t_{2}}}}}

Поступая аналогичным образом и далее до последнего платежа, окончательно получим формулу дисконтированной стоимости всего денежного потока

{displaystyle PV=sum _{k=1}^{n}{frac {CF_{k}}{(1+i)^{t_{k}}}}}

Интерпретация

При вложении суммы PV на период до {displaystyle t>=t_{n}} под ставку i будет в конечном итоге получена сумма:

{displaystyle FV=PV*(1+i)^{t}=sum _{k=1}^{n}CF_{k}(1+i)^{t-t_{k}}}

Таким образом, эта сумма равна сумме, которая будет получена в этот же момент, если последовательно под ту же ставку вкладывать отдельные элементы потока до времени t. Таким образом, дисконтированная стоимость денежного потока равна дисконтированной стоимости наращенной суммы этого потока.

Если платежи осуществляются через равные промежутки времени, то формулу можно записать без дополнительного индекса нумерации платежей k. Время t и будет представлять просто номер платежа:

{displaystyle PV=sum _{t=1}^{n}{frac {CF_{t}}{(1+i)^{t}}}}

В этих формулах время измеряется в единицах периода ставки дисконтирования i. Обычно ставка даётся годовая, а время может быть дано в днях, месяцах, кварталах и т. д. В этом случае в качестве времени используют отношение времени в заданных единицах к продолжительности года в тех же единицах (например, если выплата через квартал, то это 0,25 года). Если платежи осуществляются через равные промежутки времени, пересчитывают ставку на этот период по формуле сложных процентов: {displaystyle i'=(1+i)^{1/T}-1}, где T — продолжительность года в единицах этого периода (например для ежемесячного платежа — это 12, для ежеквартального — 4 и т. д.).

Пример[править | править код]

Имеется облигация номиналом в 1000 рублей со сроком до погашения 1 год и ежеквартальным купоном 20 рублей, что соответствует купонной ставке 8 % годовых (20 x 4 / 1000 = 0,08). Владелец облигации получает в первые три квартала по 20 рублей, а в четвёртом квартале — 20 рублей и сумму погашения. Таким образом, структура выплат следующая: 20 + 20 + 20 + 1020. Периоды между платежами равные.

Теперь продисконтируем данный поток платежей. Допустим, ставка дисконтирования равна 6,14 % годовых (например, это ожидаемая инфляция или 5,5 % безрисковая ставка плюс премия за риск 0,64 % для инструментов с данным риском — цифра условная для примера). Можно посчитать квартальную ставку как {displaystyle 1{,}0614^{1/4}-1} получаем примерно 1,5 % в квартал. Таким образом, дисконтированная стоимость данного потока платежей при квартальной ставке в 1,5 % будет равна

{displaystyle {frac {20}{1{,}015}}+{frac {20}{1{,}015^{2}}}+{frac {20}{1{,}015^{3}}}+{frac {1020}{1{,}015^{4}}}=19{,}704+19{,}413+19{,}126+960{,}995=1019{,}24}

То же самое можно рассчитать непосредственно через годовую ставку, не рассчитывая квартальную ставку, а используя время в долях от года:

{displaystyle {frac {20}{1{,}0614^{0{,}25}}}+{frac {20}{1{,}0614^{0{,}5}}}+{frac {20}{1{,}0614^{0{,}75}}}+{frac {1020}{1{,}0614}}=1019{,}24}

Дисконтированная стоимость некоторых денежных потоков[править | править код]

Дисконтированная стоимость аннуитета[править | править код]

Если поток платежей аннуитетный, то есть платежи имеют одинаковую величину и выплачиваются через равные промежутки времени, то эта формула принимает вид (исходя из известной формулы суммы геометрической прогрессии):

{displaystyle PV,=,{frac {CF}{i}}cdot [1-{frac {1}{left(1+iright)^{n}}}],=,CFcdot {frac {1-(1+i)^{-n}}{i}}},

где {displaystyle CF} — аннуитетный платёж, осуществляемый n раз; i — ставка дисконтирования; PV — дисконтированная стоимость аннуитетных платежей {displaystyle CF}.

Дисконтированная стоимость вечных аннуитетов (перпетуитетов)[править | править код]

Для вечного аннуитета, то есть при бесконечно большом n, выражение в квадратных скобках в формуле дисконтированной стоимости аннуитета, становится равным единице, поэтому формула ещё более упрощается:

{displaystyle PV,=,{frac {CF}{i}}}

Дисконтированная стоимость платежей с постоянным темпом роста[править | править код]

Если платежи растут с постоянным темпом прироста g, то их дисконтированная стоимость вычисляется по формуле:

{displaystyle PV,=,{CF_{1} over i-g}left[1-left({1+g over 1+i}right)^{n}right]},

где {displaystyle CF_{1}} — платёж, осуществляемый в первый период, n — число периодов, i — ставка дисконтирования.

В пределе (при бесконечно большом n) при {displaystyle g<i} получается следующая простая формула (модели Гордона):

{displaystyle PV,=,{CF_{1} over i-g}}

Связанные понятия[править | править код]

  • Чистый дисконтированный доход (ЧДД) или чистая дисконтированная (приведённая, текущая) стоимость (Net Present Value, NPV) — дисконтированная стоимость будущих доходов от инвестиционного проекта за минусом (дисконтированной) стоимости вложений в проект. Характеризует эффективность инвестиционного проекта и является одним из критериев выбора инвестиционных проектов.

См. также[править | править код]

  • Дисконтированный срок окупаемости

Примечания[править | править код]

Литература[править | править код]

  • Ширяев А. Н. Основы стохастической финансовой математики. — М.: ФАЗИС, 1998. — Т. 1. Факты. Модели. — 512 с. — ISBN 5-7036-0043-X.
Источник

Как определить дисконтированную стоимость

Дисконтированная (текущая) стоимость представляет собой оценку величины полученной в будущем прибыли от вложения средств в определенный финансовый инструмент в пересчете на нынешний момент времени. Она позволяет найти размер инвестиций, который необходим для того, чтобы получать определенную прибыль по истечении установленного периода.

Как определить дисконтированную стоимость

Инструкция

Для того чтобы понять, как найти дисконтированную стоимость, рассмотрим пример. Инвестор собирается вложить денежные средства в акции. Через год он планирует получить 2000 долларов. Ставка процента (доходность) равна 10%. Для того чтобы определить дисконтированную стоимость, нужно величину будущего дохода разделить на ставку процента, увеличенную на единицу. Дисконтированная стоимость в данном примере будет составлять 1818 долларов (2000/(1+0,1)). Таким образом, инвестору нужно вложить 1818 долларов, чтобы через год получить 2000 долларов. Очевидно, что чем выше процентная ставка, тем меньшая сумма вложений потребуется, и наоборот, при меньшей процентной ставке необходимо вложить большую сумму для получения равного дохода.

Вы должны понимать, что дисконтированная стоимость зависит не только от процентной ставки, но и от срока вложений денежных средств. Допустим, инвестор вложил средства в акции на срок 3 года, а не на год, как это было указано в предыдущем примере. В этом случае дисконтированная стоимость за 1 год будет составлять 1818 долларов, за второй – 1652 доллара (1818/(1+0,1)), за третий – 1501 доллар (1652/(1+0,1)). Дисконтированная стоимость, равная 1501 доллару, означает, что инвестору для того, чтобы получить 2000 долларов через 3 года, нужно вложить данную сумму. Таким образом, чем больше срок инвестирования, тем меньшая величина инвестиций потребуется.

Для того чтобы определить дисконтированную стоимость при различных сроках инвестирования и процентных ставках, используйте следующую формулу:P=I/(1+r)^n, где Р – дисконтированная стоимость; I – величина инвестиций; r – процентная ставка; n – срок инвестирования.Необходимость расчета дисконтированной стоимостью обусловлена тем, что она позволяет соотнести предполагаемую сумму вложений с ожидаемой величиной прибыли. На основании чего можно сделать вывод, целесообразно ли вкладывать средства в рассматриваемый проект.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Дисконтирование как способ определения справедливой стоимости для целей МСФО

КФО № 10 2014

Леснова Ю.В.,
директор ООО АФ «Аудиторско-консалтинговый центр»

Статья предоставлена редакцией журнала «Корпоративная финансовая отчетность. Международные стандарты» в рамках совместного проекта «Методология МСФО для компаний и экспертов» Издательского дома «Методология» и Финансовой академией «Актив» для экспертов в области МСФО.

Вся методология МСФО, комментарии экспертов, практические разработки, отраслевые рекомендации доступны при годовой и полугодовой подписке на журнал.

Временная стоимость денег — это один из основных принципов отражения операций по финансированию бизнеса. Временная стоимость денег связана с процентными ставками, сложным процентом, понятием времени и рисками в отношении денежных средств и их потоков. Любая компания представляет собой объект инвестиций, то есть, привлекая сегодня денежные средства от инвесторов, компания должна через время обеспечить возврат долга инвестору (кредитору, акционеру) и произвести выплату вознаграждения за эти инвестиции.

В основе концепции временной стоимости денег лежит следующее: значение одной денежной единицы, которая есть в наличии в настоящее время, больше, чем значение одной денежной единицы, которую получим в будущем. Происходит это по трем причинам. Во-первых, денежная единица может быть инвестирована в настоящее время и в этом случае будут заработаны проценты на протяжении времени инвестирования. Во-вторых, деньги подвержены инфляции, то есть с течением времени уменьшается их покупательная способность, что делает стоимость денег меньшей в будущем, так как сегодня можно купить на эти деньги больше, чем на эти же деньги в будущем. В-третьих, всегда есть риск не получить вложенные деньги обратно в будущем, при этом если вы имеете денежные средства в настоящий момент, то в таком случае нет никакого риска, что это произойдет.

Концепция временной стоимости позволяет инвестору учесть вышеизложенные причины при принятии финансовых решений путем оценки денежных потоков в различные периоды времени, на основании преобразования денежных потоков на текущий момент или на будущий момент времени.

Основы дисконтирования

Временная стоимость денег включает в себя понятия будущей стоимости (компаундирование) и текущей стоимости (дисконтирование).

В расчетах используются четыре основных типа временной стоимости денег:

  • будущая стоимость единовременного платежа,
  • будущая стоимость аннуитета,
  • приведенная стоимость единовременного платежа,
  • приведенная стоимость аннуитета.

В финансовом учете используется дисконтирование денежных потоков, чтобы обеспечить сопоставимость данных финансовой отчетности разных компаний, разных отчетных периодов. Кроме того, дисконтирование позволяет четко определить финансовые расходы за отчетный период с учетом особенности финансирования конкретной компании.

В целом операции дисконтирования сводятся к формуле дисконтирования:

PV = FV / (1 + i)n,

где PV — текущая стоимость;
FV — будущая стоимость;
i — ставка дисконтирования;
n — срок (число периодов).

Для того чтобы определить будущую стоимость, следует преобразовать формулу:

FV = PV × (1 + i)n,

Пример 1

Компания хочет иметь 1 млн руб. через год, при условии процентной ставки 10 % годовых. Сумма, которую необходимо вложить в настоящий момент, составит:

PV = FV / (1 + i)n = 1 000 000 / 1,1 = 909 091 руб.

Пример 2

Компания хочет иметь 1 млн руб. через 3 года, при условии процентной ставки 10 % годовых. Сумма, которую необходимо вложить в настоящий момент, составит:

PV = FV / (1 + i)n = 1 000 000 / 1,331 = 751 315 руб.

В МСФО вопросы дисконтирования представлены в нескольких стандартах, но особенно детально они описаны в МСФО (IFRS) 13 «Оценка справедливой стоимости» и МСФО (IAS) 36 «Обесценение активов».

Дисконтирование в МСФО (IFRS) 13

В МСФО (IFRS) 13 «Оценка справедливой стоимости» приведены методы оценки справедливой стоимости, предусматривающие дисконтирование, в случае применения доходного подхода при определении справедливой стоимости.
При использовании доходного подхода при оценке справедливой стоимости будущие суммы (например, потоки денежных средств или доходы и расходы) преобразовываются в единую сумму на текущий момент (то есть дисконтированную). А результат оценки справедливой стоимости отражает текущие рыночные ожидания в отношении таких будущих сумм.
Метод оценки по приведенной стоимости, используемый для определения справедливой стоимости, будет зависеть от фактов и обстоятельств, специфических для оцениваемого актива или обязательства (например, наблюдаются ли цены на сопоставимые активы или обязательства на рынке), и наличия достаточных данных. Можно утверждать, что при использовании данного метода могут применяться наблюдаемые данные (например, безрисковая ставка на капитал).

Справочно

Согласно пункту B13 МСФО (IFRS) 13 приведенная стоимость (то есть применение доходного подхода) — это инструмент, используемый для связывания будущих сумм (например, потоков денежных средств или значений стоимости) c существующей суммой с использованием ставки дисконтирования.

Определение справедливой стоимости по приведенной стоимости основано на предположении о том, что потенциальный инвестор (покупатель) не заплатит сумму, превышающую текущую стоимость будущих денежных потоков; в свою очередь, продавец не продаст по цене, которая ниже текущей стоимости прогнозируемых будущих доходов. В результате такого равновесия стороны придут к соглашению о рыночной цене, равной текущей стоимости будущих доходов.

По сути, подход, основанный на приведенной стоимости денежных потоков, оказывается более подходящим оценочным методом, когда текущая деятельность может дать определенное представление о том, какой она станет в будущем, включая предположения о дальнейших темпах роста.

Определение справедливой стоимости актива или обязательства с использованием метода оценки по приведенной стоимости охватывает все следующие элементы с точки зрения участников рынка на дату оценки:

  • оценку будущих потоков денежных средств от оцениваемого актива или обязательства;
  • ожидания в отношении возможных изменений суммы и времени получения потоков денежных средств, представляющих неопределенность, присущую потокам денежных средств;
  • временную стоимость денег, представленную ставкой по безрисковым монетарным активам, сроки погашения или сроки действия которых совпадают с периодом, охватываемым потоками денежных средств, и которые не представляют никакой неопределенности в отношении сроков и риска дефолта для их держателя (то есть безрисковую ставку вознаграждения);
  • цену, уплачиваемую за принятие неопределенности, присущей потокам денежных средств (то есть премию за риск);
    другие факторы, которые участники рынка приняли бы во внимание в сложившихся обстоятельствах;
  • риск невыполнения обязательств, относящийся к данному обязательству, включая собственный кредитный риск предприятия (то есть лица, принявшего на себя обязательство).

Общие принципы применения любого метода оценки по приведенной стоимости состоят в следующем:

  • Потоки денежных средств и ставки дисконтирования должны отражать допущения, которые использовались бы участниками рынка при установлении цены на актив или обязательство.
  • Для потоков денежных средств и ставок дисконтирования должны учитываться только те факторы, которые относятся к оцениваемому активу или обязательству.
  • Для того чтобы избежать двойного учета или не упустить влияние факторов риска, ставки дисконтирования должны отражать допущения, совместимые с допущениями, присущими потокам денежных средств.
  • Допущения в отношении потоков денежных средств и ставок дисконтирования должны быть последовательными между собой. Например, номинальные потоки денежных средств, которые включают эффект инфляции, должны дисконтироваться по ставке, включающей эффект инфляции. Номинальная безрисковая ставка вознаграждения включает эффект инфляции. Фактические потоки денежных средств, исключающие эффект инфляции, должны дисконтироваться по ставке, исключающей эффект инфляции. Аналогичным образом потоки денежных средств за вычетом налогов должны дисконтироваться с использованием ставки дисконтирования за вычетом налогов. Потоки денежных средств до уплаты налогов должны дисконтироваться по ставке, совместимой с указанными потоками денежных средств.
  • Ставки дисконтирования должны учитывать основополагающие экономические факторы, связанные с валютой, в которой выражены потоки денежных средств.

Пример 3

Компания А осуществляет оценку справедливой стоимости активов по приведенной стоимости. Для расчета у компании имеются данные реальной доходности по активам в размере 10 % годовых. Ожидаемые темпы инфляции — 5 % в год, поэтому компания отражает денежные потоки с учетом темпа инфляции. Чтобы определить приведенную стоимость денежных потоков, компания должна для дисконтирования использовать номинальную ставку процента. Для этого можно применить формулу Фишера:

1 + Номинальная ставка процента =
= (1 + Реальная ставка процента) × (1 + Процент инфляции).

Таким образом, компания А дисконтировать денежные потоки будет по номинальной ставке:

[(1 + 0,1) × (1 + 0,05)] − 1 = 15,5 %.

Пример 4

Компания А рассчитывает справедливую стоимость оборудования. Стоимость капитала после налогообложения по номинальной стоимости составляет 10 %. Допустим, инфляция составляет 3 % в год. Имеется следующая информация о денежных потоках по номинальной стоимости:

Таким образом, справедливая стоимость актива составляет 30 192 тыс. руб.

Рассмотрим дисконтирование денежных потоков по реальной стоимости.

(1 + Реальная ставка процента) =
(1 + Номинальная ставка процента) / (1 + Процент инфляции) =
(1 + 0,1) / (1 + 0,03) = 6,8 %

В данном случае справедливая стоимость актива составит 30 194 тыс. руб.

Таким образом, справедливая стоимость, определенная методом дисконтирования по номинальной стоимости, и дисконтированная по реальной стоимости имеют одинаковый результат.

Пример 5

На 1 января 2014 года компания имеет обязательство по выводу из эксплуатации оборудования по окончании срока полезного использования, который оценивается в 10 лет. Компания провела оценку расходов на выполнение обязательства и определила прочие условия, связанные с его выполнением:

  • Ожидаемый отток денежных средств на выполнение работ подрядчиком — 1500 тыс. руб. Подрядчик, как правило, требует компенсацию за риск того, что фактические оттоки денежных средств могут отличаться от предполагаемых из-за неопределенности, присущей сроку выполнения, который наступит через 10 лет. По оценкам компании, размер такой компенсации составляет 10 % с учетом инфляции.
  • Ожидаемый отток на оплату накладных расходов компании — 1000 тыс. руб.
  • Ожидаемый уровень инфляции — 4 % в год.
  • Безрисковая ставка по состоянию на 1 января 2014 года для срока 10 лет составляет 5 %. Компания корректирует этот показатель на 3,5 % с учетом риска невыполнения. Таким образом, ставка дисконтирования с учетом риска составляет 8,5 %.

Справедливая стоимость обязательства будет рассчитываться с использованием дисконтирования денежных потоков следующим образом:

Таким образом, справедливая стоимость обязательства составляет 1800,33 тыс. руб.

Метод дисконтирования денежных потоков

Методом дисконтирования денежных потоков инвесторы оценивают будущие ожидаемые денежные потоки и дисконтируют их по ставке доходности, которая учитывает временную стоимость денег и относительные риски инвестиций.
Можно представить метод дисконтирования денежных потоков следующей формулой:

DCF = CF1 / (1 + k) + CF2 / (1 + k)2 + CFn / (1 + k)n,

где DCF — дисконтированный денежный поток;
CF1, CF2, CFn — денежные потоки по периодам;
k — ставка дисконтирования.

Свободный денежный поток компании представляет собой денежный поток от актива до выплаты каких-либо долговых платежей. В операционных денежных потоках не учитываются проценты и их влияние на налоги, так как этот фактор непосредственно учитывается в коэффициенте дисконтирования.

При оценке будущих ожидаемых денежных потоков обычно выделяют следующие типы рисков:

  • единичный риск;
  • рыночный риск.

    • Единичный риск представляет собой неопределенности, присущие ожидаемым денежным потокам.

    Метод оценки риска

    Метод оценки риска — это использование метода статистической вероятности. При применении метода оценки по ожидаемой приведенной стоимости используется набор потоков денежных средств, который представляет взвешенное с учетом вероятности среднее значение всех возможных будущих потоков денежных средств. Получаемая в результате расчетная величина идентична ожидаемой стоимости, которая в статистическом выражении является средневзвешенным значением возможной стоимости дискретной случайной переменной с соответствующей взвешиваемой вероятностью. Поскольку все возможные потоки денежных средств взвешиваются с учетом вероятности, получаемый в результате ожидаемый поток денежных средств не является условным и не зависит от возникновения какого-либо определенного события.

    Пример 6

    Компания А рассчитывает справедливую стоимость оборудования. Стоимость капитала компании составляет 10 %. Имеется следующая информация о распределении вероятности поступления денежных потоков:

    Рассчитаем дисконтированную стоимость денежных потоков.

    В данном случае справедливая стоимость актива составит 24 693 тыс. руб.

    Следует отметить, что на практике может существовать много возможных результатов (исходов). Однако для того чтобы применить метод оценки по ожидаемой приведенной стоимости, не всегда нужно учитывать распределение всех возможных потоков денежных средств, используя сложные модели и методы. Вместо этого можно разработать ограниченное количество дискретных сценариев и вероятностей, которые охватывают множество возможных потоков денежных средств.

    Ставка дисконтирования

    Приведение спрогнозированных денежных потоков в текущую стоимость осуществляется с помощью ставки дисконтирования.

    Справочно

    Ставка дисконтирования — это норма доходности, которую желает получать инвестор от вложенных средств. При этом важной составляющей нормы доходности является компенсация за риск, связанный с инвестированием.

    Следует отметить, что ставка дисконтирования не зависит от структуры капитала компании и способа, с помощью которого компания финансировала приобретение актива, поскольку будущие потоки денежных средств, ожидаемые от актива, не зависят от того, каким образом компания финансировала приобретение актива. Применяемая ставка дисконтирования должна соответствовать типу денежного потока.

    Ставки дисконтирования можно также подразделить следующим образом:

    • ставка дисконтирования для собственного капитала;
    • ставка дисконтирования для заемного капитала.

    Взаимосвязь ставки дисконтирования для собственного капитала и ставки дисконтирования для заемного капитала характеризуется следующей формулой средневзвешенной стоимости капитала (WACC):

    WACC = Ke × We + Kp × Wp + Kd × Wd × (1 × T),

    где Ke — стоимость обыкновенных акций, %;
    We — доля обыкновенных акций в структуре капитала;
    Kp — стоимость привилегированных акций, %;
    Wp — доля привилегированных акций в структуре капитала;
    Kd — стоимость заемного капитала, %;
    Wd — доля заемного капитала в структуре капитала;
    T — ставка налога на прибыль, %.

    Расчет стоимости собственного капитала ставки на основе модели дисконтирования дивидендов (kр) рассчитывается по следующей формуле:

    kр = D / P,

    где D — фиксированный размер выплачиваемых дивидендов;
    Р — рыночная цена одной акции в настоящий момент.

    Данный расчет основывается на следующих предположениях:

    • существует развитый высоколиквидный рынок акций;
    • оценка финансового актива может осуществляться по прогнозируемым потокам платежей, получаемых владельцами капитала;
    • дивиденды по акциям фиксированы и не меняются по годам;
    • срок обращения акций не ограничен.

    Расчет стоимости собственного капитала на основе модели стоимости обыкновенных акций (kе) с прогнозируемым приростом дивидендов основывается на формуле:

    kе = (D1 / P0) + g,

    где D1 — денежные дивиденды на одну акцию, выплата которых ожидается в конце первого периода;
    Р0 — рыночная цена одной акции в настоящий момент;
    g — прогнозируемый ежегодный рост дивидендов.

    Данный метод лучше всего подходит для компаний, растущих со скоростью, не превышающей скорости номинального роста в экономике, с хорошо установленной политикой выплаты дивидендов, и эти выплаты они намерены производить и в будущем.

    Стоимость собственного капитала рассчитывается также на основе модели оценки капитальных активов (САРМ). Модель оценки капитальных активов предусматривает, что ожидаемая доходность инвестора складывается из двух компонентов: безрисковой ставки доходности и премии за риск инвестирования. Сама же премия за риск корректируется на систематический риск актива. Систематический риск обозначается бета-коэффициентом (β).

    Важнейшие из предположений в данной модели:

    • для всех инвесторов период вложения одинаков;
    • информация свободно и незамедлительно доступна для всех инвесторов;
    • инвесторы имеют однородные ожидания, то есть одинаково оценивают будущие доходности, риск и ковариации доходностей ценных бумаг;
    • безрисковая процентная ставка одинакова для всех инвесторов.

    Ниже представлена формула расчета стоимости собственного капитала (Re) по модели САРМ:

    Re = Rf + (Rm − Rf ) × β,

    где Rf — безрисковая ставка доходности, %;
    Rm — рыночная доходность собственного капитала, %;
    (Rm − Rf) — премия за риск, %;
    β — бета-коэффициент, характеризующий риск компании.

    Считается, что безрисковая ставка доходности одинакова для всех инвесторов. В качестве безрисковой ставки могут использоваться государственные облигации страны-эмитента.

    Метод CAPM является наиболее рыночным. При наличии развитого фондового рынка в оценочной практике данный метод применяется наиболее часто.

    Таким образом, принцип временной стоимости денег используется в финансовом учете для отражения ряда операций, например связанных с учетом сделок по долгосрочным займам, финансовой аренде, кредиторской и дебиторской задолженности, с учетом операций с векселями и облигациями, для отражения амортизации премий и дисконтов (скидок) по облигациям, для оценки компонентов затрат и многого другого.

    Принцип временной стоимости денег является основой в области финансов, он дает понимание ценности денег во времени, имеет решающее значение для определения ожидаемой отдачи от вложенных инвестиций.

    Разберитесь в теме оценки справедливой стоимости глубже на курсе «ДипИФР. Гарантия»!

    Зарегистрируйтесь и посмотрите 3 урока бесплатно!

    Проверьте себя. Какой метод дисконтирования используется в компаниях с установленной политикой выплаты дивидендов?

Источник

Добавить комментарий