Что такое ставка дисконтирования, для чего она нужна и как ее рассчитывать. Рассказываем об этом в нашем обзоре

В этой статье вы узнаете
- Что это
- Как появилась
- Как рассчитать
- Интуитивные методы определения ставки
- Модели расчета на основе премий за риск
- Аналитические методы расчета
- Как применяется
Что такое ставка дисконтирования
Ставка дисконтирования — это эталонная величина, выраженная в процентах, применяемая для сравнительной оценки эффективности инвестиций.
Например, вам нужно выбрать: положить деньги в банк со ставкой депозита 12% сроком на пять лет с ежегодной выплатой процента или купить
облигации
с погашением через девять лет с купоном 8,5%, выплачиваемым дважды в год и с текущей ценой 91% от номинала. Как вы будете выбирать, да еще учитывая, что уровень инфляции составляет около 8%?

Аналитик занимается оценкой стоимости
(Фото: Shutterstock)
Для решения этих задач используется прием, который называют дисконтированием. С помощью дисконтирования можно сопоставить будущие денежные потоки и выбрать из нескольких вариантов инвестиций самый выгодный. А ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.
Правильный расчет ставки дисконтирования позволит вам:
- оценить эффективность инвестиций относительно надежных вкладов;
- сравнить варианты инвестиций с разной длительностью вложения;
- сравнивать доходность вложений инструментов с разной степенью риска.
Ставка дисконтирования зависит от множества факторов: уровень инфляции, доступные для инвестора варианты вложений, риск вложений, стоимость вашего капитала и др. Но далеко не все внешние факторы можно достоверно учесть в ставке.
Как появилась ставка дисконтирования
Первоначально ставка дисконтирования применялась при учете векселей. Принимая к оплате вексель, банкиры знали сумму, которую они получат, когда предъявят вексель к погашению. Но чтобы им самим заработать, банкиры выплачивали предъявителю деньги со скидкой — дисконтом. А процентная ставка, в которой измерялся их доход, называлась учетной ставкой, или ставкой дисконтирования (discount rate). Сумма, которая выплачивалась предъявителю векселя, рассчитывалась как раз с помощью дисконтирования — зная, сколько он получит в будущем и учитывая текущий уровень процентных ставок, банкир определял текущую стоимость денег.
Этот прием оказался настолько универсальным и полезным, что стал широко применяться при оценке и сравнении эффективности вложений в разные инструменты или проекты. При дисконтировании инвестор, как и банкир при учете векселей, пересчитывает стоимость денег, которые он получит в будущем, причем в совершенно разные сроки, на текущую стоимость. Он как бы проецирует стоимость денег из будущего на плоскость настоящего времени. А центральным звеном расчетов выступает ставка дисконтирования.

Как рассчитать ставку дисконтирования
При расчете ставки дисконтирования очень важно определить ставку, которая позволит максимально корректно привести будущую стоимость доходов и расходов к текущей. Для этого нужно учитывать и общий уровень процентных ставок, и факторы риска вложений в отдельные инструменты.
При расчете ставки дисконтирования нужно учесть два основных вида факторов:
- Уровень безрисковых ставок.
- Премии за риск.
Безрисковые ставки — это процентные ставки инструментов с минимальным для инвестора уровнем риска. Обычно такими инструментами являются облигации центрального правительства — ОФЗ в России, US Treasuries в США и т. п. Также в качестве безрисковых ставок могут учитываться ставки по депозитам системообразующих банков. Иногда как безрисковая ставка может рассматриваться ключевая ставка центральных банков.
Уровень безрисковых ставок является фундаментальным — он определяет минимальный уровень всех ставок дисконтирования.
Премии за риск — это надбавки к уровню безрисковых ставок, которые стоит учитывать при вложении в отдельные инструменты или проекты. Это могут быть общие факторы — уровень инфляции, надбавка за страновой риск; факторы, учитывающие риск вложения в отдельные инструменты, — надбавка за отраслевой риск, надбавка за индивидуальный риск (зависит от надежности эмитента, инструмента или проекта).
Учет премий за риск позволит более точно настроить инструмент дисконтирования, чтобы избежать ошибок в сравнении разных инвестиций.
При расчете ставки дисконтирования используются различные способы и методы, которые можно объединить в такие основные группы:
- интуитивные методы;
- модели на основе премий за риск;
- аналитические модели.
Интуитивные методы
В эту группу включается:
- собственно интуитивный метод.
- экспертный метод.
Интуитивный метод — это способ определения ставки дисконтирования на основе субъективного видения инвестора. Проще говоря, когда инвестор прикидывает ставку дисконтирования практически на глазок. Например, он рассуждает так: «Я могу положить деньги на депозит в надежном банке под 12–15%. Тогда эффективность других вложений я буду сравнивать с таким уровнем ставок».
Экспертный метод — это, по сути, тот же интуитивный метод, только итоговая величина ставки дисконтирования выводится как совокупный консенсус нескольких экспертов с тем или иным уровнем обоснованности их мнений.

Аналитики совещаются
(Фото: Shutterstock)
Модели на основе премий за риск
К моделям на основе премий за риск относятся, например, такие модели, как:
- модель кумулятивного построения;
- модель капитальных активов CAPM.
Общим для этих моделей является то, что ставка дисконтирования выводится как сумма безрисковой ставки и премий за риск.
Модели кумулятивного построения — это метод определения ставки дисконтирования, при котором к безрисковой процентной ставке прибавляются все премии за риск, которые можно определить для конкретного инструмента.
Формула расчета ставки дисконтирования кумулятивным способом выглядит так:
![]()
где r0 — безрисковая ставка,
r1, r2, rn — все премии за риск для оцениваемого инструмента.
Модель капитальных активов CAPM (Capital Asset Pricing Model, модель оценки капитальных активов) — это метод определения ставки дисконтирования для сравнительной оценки эффективности вложений в акции, при котором к безрисковой процентной ставке прибавляется премия за риск по отдельному инструменту с учетом его β-коэффициента.
β-коэффициент (бета-коэффициент) — это мера рыночного риска акции, которая показывает изменчивость доходности акции к доходности на рынке в среднем. β-коэффициент численно показывает, на сколько процентов изменяется цена акции бумаги при росте или снижении индекса на 1%. Положительный коэффициент говорит о том, что акция двигается в одном направлении с рынком, а отрицательный коэффициент означает, что акция двигается в противоположную от общего направления рынка сторону.
β-коэффициенты рассчитываются и публикуются и аналитиками, и торговыми площадками, например Московской биржей.
Формула расчета ставки дисконтирования по CAPM выглядит так:
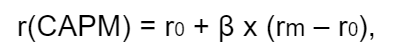
где r0 — безрисковая ставка,
β — β-коэффициент,
rf — средняя доходность фондового рынка (биржевого индекса).

Аналитические диаграммы
(Фото: Shutterstock)
Аналитические методы
Аналитические методы — способы расчета ставки дисконтирования с применением элементов финансового анализа. Среди аналитических методов можно выделить:
- WACC;
- мультипликативные методы.
WACC — это средневзвешенная стоимость капитала (Weighted Average Cost of Capital). WACC используется компаниями для сравнительной оценки эффективности инвестиционных проектов.
Как правило, у компании есть два вида используемого капитала — собственный и заемный. Собственный капитал равен сумме средств, принадлежащих самой компании или причитающихся ее акционерам. Заемный капитал — это средства, привлеченные компанией извне (кредиты и займы). Заемный капитал достается компании не бесплатно — по кредитам и займам она должна платить проценты.
В случае когда у компании или у инвестора только заемные деньги, то для них самым главным становится то, чтобы инвестиционные проекты приносили больше, чем приходится платить по кредиту. В этом случае при оценке инвестиционных проектов в качестве ставки дисконтирования можно использовать ставку по кредиту, скорректированную на ставку налога на прибыль.
Но когда у компании есть и собственный, и заемный капитал, то ставка дисконтирования по модели WACC считается следующим образом:
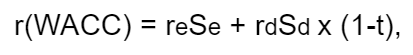
где re — стоимость собственного капитала,
Se — доля собственного капитала,
rd — стоимость заемного капитала,
Sd — доля заемного капитала,
t — ставка налога на прибыль.
Стоимость заемного капитала rd — это средневзвешенный процент по имеющимся займам и кредитам.
Стоимость собственного капитала re может определяться либо методом CAPM, описанным выше, либо другим способом — например, с помощью модели Гордона.
Модель Гордона для оценки стоимости собственного капитала компании предполагает, что за возможность использования собственного капитала компания платит дивидендами. Значит, стоимость собственного капитала определяется отношением суммы выплаченных дивидендов к сумме денег, привлеченных в ходе размещения акций.
В итоге формула, по которой рассчитывается стоимость собственного капитала по Гордону, выглядит так:
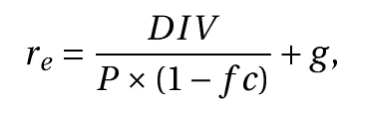
где DIV — это сумма годовых ожидаемых дивидендов на одну акцию;
P — цена размещения акций,
fc — затраты на эмиссию (в %),
g — темпы прироста дивидендов.
Мультипликативные методы — это способы расчета ставки дисконтирования на основе различных коэффициентов прироста и других коэффициентов предприятий.
Это может быть, например:
- расчет ставки на основе рентабельности капитала (ROE), когда за ставку дисконтирования принимают показатель ROE;
- расчет ставки на основе рентабельности активов (ROA), когда за ставку дисконтирования принимают показатель ROA;
- расчет ставки на основе рыночных мультипликаторов, когда за ставку дисконтирования принимают значение доходности как отношения прогнозного дохода к текущей рыночной стоимости компании. Например, прогнозное значение чистой прибыли на акцию (EPS) к рыночной стоимости акций или прогнозное значение денежного потока к капитализации

Как применяется ставка дисконтирования
Как мы писали вначале, ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.
Дисконтирование — это приведение будущей стоимости денежных потоков к стоимости в настоящее время по ставке дисконтирования.
Один из частых результатов дисконтирования — получение чистой текущей (приведенной) стоимости денег.
Чистая текущая стоимость (NPV, Net Present Value) — разница между всеми денежными притоками и оттоками, приведенными к текущему моменту времени по ставке дисконтирования. Эта величина показывает сумму денежных средств, которую инвестор ожидает получить от проекта, пересчитанную к настоящему времени.
Сравнив NPV разных по длительности инвестиционных вариантов, инвестор может выбрать наиболее доходный.
Узнайте о возможностях нашего Каталога в телеграм-канале «РБК Инвестиций»
Долговая ценная бумага, владелец которой имеет право получить от выпустившего облигацию лица, ее номинальную стоимость в оговоренный срок. Помимо этого облигация предполагает право владельца получать процент от ее номинальной стоимости либо иные имущественные права.
Облигации являются эквивалентом займа и по своему принципу схожи с процессом кредитования. Выпускать облигации могут как государства, так и частные компании.
ОПРЕДЕЛЕНИЕ
КУРСОВОЙ СТОИМОСТИ И
ДОХОДНОСТИ
ВЕКСЕЛЯ
1.
Дисконтный вексель
1.
1. Определение дисконта и ставки дисконта
Дисконтные
векселя котируются на основе ставки
дисконта. Она говорит о величине скидки,
которую продавец предоставляет
покупателю. Ставка дисконта указывается
в процентах к номиналу векселя как
простой процент в расчете на год. Ставку
дисконта можно пересчитать в рублевый
эквивалент с помощью формулы:
![]() (1)
(1)
где:
D
—
дисконт векселя; N
—
номинал векселя; d
— ставка
дисконта; t
—
число дней с момента приобретения
векселя до его погашения. В знаменателе
указывается 360 дней, поскольку расчеты
с векселем осуществляются на базе
финансового года, равного 360 дням.
Пример
1.
N
=
100 млн. руб., d
– 20%,
t = 45 дней. Определить величину скидки.
Решение.
Она
равна:
![]() =250
=250
тыс.
руб.
***
Ставка
дисконта определяется по формуле:
![]() (2)
(2)
Пример
2.
N
=10
млн. руб., D
=
100 тыс. руб., до погашения остается 50
дней. Определить ставку дисконта.
Решение.
Она
равна:
![]() =0,072
=0,072
или 7,2%
***
1.
2. Определение цены векселя
Цену
векселя можно определить, вычтя из
номинала величину скидки, а именно:
P
=
N
−
D
(3)
где:
Р
— цена
векселя.
Если
известна ставка дисконта, то цена
определяется по формуле:
![]() (4)
(4)
Пример
3.
N
= 10
млн. руб., d
=
6%, до погашения остается 15 дней. Определить
цену векселя.
Решение.
Она
равна:
![]() =9975
=9975
тыс. руб.
***
Если
инвестор определил для себя значение
доходности, которую бы он желал обеспечить
по векселю, то цену бумаги можно вычислить
по формуле:
 (5)
(5)
где:
r
— доходность,
которую желает обеспечить себе инвестор.
(Если вкладчик сравнивает инвестиции
в вексель с другими бумагами, для которых
финансовый год равен 365 дням, то в формуле
(5) целесообразно в знаменателе ставить
цифру 365).
5.
3. 1. 3. Эквивалентная ставка дисконта,
доходность векселя
Ставка
дисконта представляет собой характеристику
доходности векселя. Однако она не
позволяет непосредственно сравнить
доходность векселя с доходностью других
ценных бумаг, так как, во-первых, она
рассчитывается на базе 360 дней, и,
во-вторых, при ее определении скидка
относится к номиналу, тогда как реально
покупатель инвестирует меньшую сумму,
а именно, цену.
Данные
обстоятельства занижают доходность
векселя. Поэтому необходимо определить
формулу для пересчета ставки дисконта
в доходность на базе 365 дней и учета
цены. Ее можно найти из следующего
равенства:
 (6)
(6)
где:
r— эквивалентная ставка доходности.
Тогда
![]() (7)
(7)
Пример
4.
Ставка
дисконта равна 20%, срок погашения
наступает через 30 дней. Определить
эквивалентную ставку.
Решение.
Она
равна:
![]() =
=
0,2062 или 20,62%
Эквивалентную
ставку также можно определить из формулы
(5), если взять финансовый год равным 365
дням:
![]() (8)
(8)
2.
Процентный вексель
2.1.
Определение суммы начисленных процентов
и
вексельной суммы
По
процентному векселю начисляются проценты
по ставке, которая указывается в векселе.
Сумму начисленных процентов можно
определить по формуле:
![]() (9)
(9)
где:
I
—
сумма начисленных процентов; N—
номинал векселя; С%
—
процентная ставка, начисляемая по
векселю;
![]()
—
количество дней от начала начисления
процента до его погашения.
Пример
5.
Номинал
векселя равен 1 млн. руб., по векселю
начисляются 25% годовых, с начала начисления
процентов до момента предъявления
векселя к оплате прошло 30 дней. Определить
сумму начисленных процентов.
Решение.
Она
равна:
![]() =20833,33
=20833,33
руб.
Общая
сумма, которую держатель процентного
векселя получит при его погашении, равна
сумме начисленных процентов и номинала.
Ее можно определить по формуле:
![]() (10)
(10)
где:
S — сумма процентов и номинала векселя.
2.2.
Определение цены векселя
Цена
векселя определяется по формуле:
 (11)
(11)
где:
Р
—
цена векселя; t
— количество
дней от покупки до погашения векселя;
r — доходность, которую желал бы обеспечить
себе инвестор.
2.
3. Определение доходности векселя
Доходность
векселя определяется по формуле:
 (12)
(12)
Пример
6.
Номинал
векселя 1 млн. руб., по векселю начисляется
25% годовых, период с момента начала
начисления процентов до погашения
бумаги равен 60 дням. Определить доходность
операции для инвестора, если он купит
вексель за 30 дней до погашения по цене
1010 тыс.руб. и предъявит его по истечении
этого срока.
Решение.
Доходность
равна:
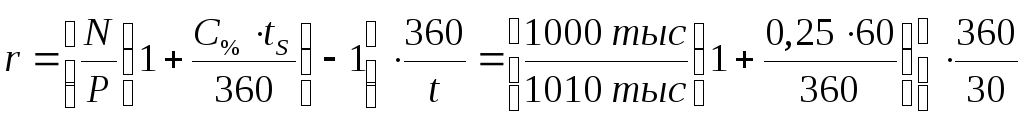 =0,3762
=0,3762
или
37,62%
Мы
представили формулы определения цены
и доходности векселей без учета
налогообложения. Корректировать формулы
на налоговые ставки следует следующим
образом: необходимо умножить суммы,
подлежащие
налогообложению,
на (1 — Tax),
где Tax
— ставка налога (ставка налога
подставляется вформулу в десятичном
значении, например, налог 15% следует
учесть в формуле как 0, 15);. Например, для
процентного векселя налоги взимаются
с суммы начисленных процентов. Поэтому
корректировке подлежит величина:
![]()
а
именно:
![]()
Задания
1.
Определите сумму дисконта веселя, если
ставка дисконта равна 10%, до погашения
векселя остается 100 дней, номинал — 1
млн. руб
2.
Чему равна цена векселя, если его номинал
100 тыс. руб., ставка дисконта — 15%, до
погашения — 30 дней.
3.
Инвестор хотел бы получить по дисконтному
векселю доходность 30% годовых. До
погашения векселя 50 дней, номинал 100
тыс. руб. По какой цене следует купить
вексель?
4.
Ставка дисконта равна 30%, до погашения
векселя 100 дней. Определите эквивалентную
ставку.
5.
Номинал процентного векселя 100 тыс.
руб., по векселю начисляется 10% годовых,
период с момента начала начисления
процентов до погашения бумаги равен 30
дням. Определите доходность операции
для инвестора, если он купит вексель за
10 дней до погашения по цене 100200руб.
5.
Номинал процентного векселя 100 тыс.
руб., по векселю начисляется 10% годовых,
период с момента начала начисления
процентов до погашения бумаги равен 30
дням. Определите, по какой цене его
должен купить инвестор за 20 дней до
погашения, чтобы обеспечить доходность
по операции на уровне 25% годовых.
Соседние файлы в папке ЛекцииМатМодРЦБ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дисконтирование стоимости векселей
- Дисконтирование стоимости векселей
- продажа или перевод векселей по стоимости ниже номинала. Стоимость дисконтируемого векселя определяется умножением величины процентной ставки на количество дней, оставшихся до наступления срока платежа, и вычетом полученного результата из номинала векселя. Уровни процентных ставок различаются в зависимости от степени надежности трассата или индоссантов.
Словарь по экономической теории. — Новосибирск: РГТЭУ, Новосибирский филиал.
.
2007.
Смотреть что такое “Дисконтирование стоимости векселей” в других словарях:
-
ДИСКОНТИРОВАНИЕ — учет векселей. Словарь финансовых терминов. Дисконтирование Дисконтирование определение текущего эквивалента денежных средств, ожидаемых к получению в определенный момент в будущем. в страховании вычисление современной стоимости будущих доходов… … Финансовый словарь
-
дисконтирование — Приведение экономических показателей к сопоставимому по времени виду путем умножения их на коэффициент дисконтирования. В частности, дисконтированием денежных потоков называют приведение их разновременных (относящихся к разным этапам оценки… … Справочник технического переводчика
-
Дисконтирование — [discounting] приведение экономических показателей разных лет к сопоставимому по времени виду. Применение дисконтирования объясняется тем, что человеку свойственно более высоко ценить сегодняшние блага (стоимости) по сравнению с будущими, и … … Экономико-математический словарь
-
Дисконтирование — DISCOUNTING 1. Расчет текущей стоимости будущих доходов и расходов, связанных с инвестиционным проектом, т.е. приведение встречных денежных потоков к общему знаменателю на основе учетной ставки. См. Discounted cash flow. 2. Учет векселей. См.… … Словарь-справочник по экономике
-
Дисконт — (Discount) Дисконт это разница между ценами на одинаковые товары с разными сроками поставки Несколько значений экономического понятия дисконт, процесс определения ставки дисконтирования из расчета норм дисконта Содержание >>>>>>> … Энциклопедия инвестора
-
Банк — (Bank) Банк это финансово кредитное учреждение, производящее операции с деньгами, ценными бумагами и драгоценными металлами Структура, деятельность и денежно кредитной политика банковской системы, сущность, функции и виды банков, активные и… … Энциклопедия инвестора
-
Инвестор — (Investor) Инвестор это лицо или организация, совершающее вложения капитала с целью получения прибыли Определение понятия инвестор, частный, квалифицированный и институциональный инвестор, особенности работы инвестора, известные инвесторы,… … Энциклопедия инвестора
-
Денежно-кредитная политика — (Monetary policy) Понятие денежно кредитной политики, цели денежно кредитной политики Информация о понятии денежно кредитной политики, цели денежно кредитной политики Содержание >>>>>>>>>> … Энциклопедия инвестора
-
Аккредитив — (Letter of credit) Понятие аккредитив, виды аккредитивов, расчеты по аккредитивам Информация о понятии аккредитив, виды аккредитивов, расчеты по аккредитивам Содержание >> Аккредитив это, определение это условное , принимаемое (банком эмитентом)… … Энциклопедия инвестора
Дисконтированная (приведённая, текущая) стоимость — оценка стоимости (текущий денежный эквивалент) будущего потока платежей исходя из различной стоимости денег, полученных в разные моменты времени (концепция временно́й ценности денег). Денежная сумма, полученная сегодня, обычно имеет более высокую стоимость, чем та же сумма, полученная в будущем. Это связано с тем, что деньги, полученные сегодня, могут принести в будущем доход после их инвестирования. Кроме того, деньги полученные в будущем в условиях инфляции обесцениваются (на ту же сумму в будущем можно приобрести меньшее количество товаров и услуг). Также есть другие факторы, снижающие стоимость будущих платежей. Неравноценность разновременных денежных сумм численно выражается в ставке дисконтирования.
Дисконтированная стоимость некоторой будущей суммы 

Дисконтированная стоимость широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объём финансовых вложений готов сделать инвестор для получения данного денежного потока. Дисконтированная стоимость будущего потока платежей является функцией ставки дисконтирования, которая может определяться в зависимости от:
- доходности альтернативных вложений;
- стоимости привлечения (заимствования) средств;
- инфляции;
- срока, через который ожидается будущий поток платежей;
- риска, связанного с данным будущим потоком платежей;
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Практическое объяснение[править | править код]
Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену вследствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб., которые будут получены через пять лет.
Наращение процентов и дисконтирование[править | править код]
Пусть некоторая денежная сумма 



Соответственно, если дана денежная сумма 




Величину 


В общем случае сумма может быть приведена к любому моменту времени (не только к текущему):

Приведение разновременных сумм к одному и тому же моменту времени делает их сопоставимыми (равноценными) с точки зрения концепции временно́й ценности денег. Предполагается, что существует возможность вложить любую сумму в любой момент времени в некоторый инструмент (например, банковский депозит) с доходностью 


Пример[править | править код]
Если через 1 год ожидается сумма 121 рубль, то при ставке дисконтирования 10 % годовых дисконтированная стоимость будет равна 

В табличных процессорах в состав финансовых функций входит функция для вычисления дисконтированной стоимости. В OpenOffice.org Calc для вычисления дисконтированной стоимости различных видов платежей применяется функция PV.
Дисконтированная стоимость денежных потоков[править | править код]
Денежные потоки[править | править код]
Денежным потоком называют распределённое во времени движение денежных средств. Во многих случаях (депозиты, кредиты, ценные бумаги и др.) денежный поток представляет собой упорядоченную по времени совокупность денежных сумм (платежей) — это так называемый дискретный денежный поток или поток платежей. Таким образом, поток платежей 



В некоторых случаях частота платежей может быть настолько большой, что денежный поток можно считать непрерывным. В частности, это имеет место для денежных потоков от обычной операционной деятельности компаний, потоков от инвестиционных проектов и т. д. Формально для непрерывных потоков можно ввести функцию плотности потока 

Таким образом, можно считать, что денежный поток CF задаётся всегда упорядоченной совокупностью денежных сумм 
Дисконтированная стоимость потока платежей[править | править код]
Дисконтированная стоимость потока платежей 



Вывод формулы
Поток платежей разобьём на первый 






Аналогичным образом можно разделить остаточный поток на платёж 


Подставив это в первую формулу получим

Поступая аналогичным образом и далее до последнего платежа, окончательно получим формулу дисконтированной стоимости всего денежного потока

Интерпретация
При вложении суммы 



Таким образом, эта сумма равна сумме, которая будет получена в этот же момент, если последовательно под ту же ставку вкладывать отдельные элементы потока до времени t. Таким образом, дисконтированная стоимость денежного потока равна дисконтированной стоимости наращенной суммы этого потока.
Если платежи осуществляются через равные промежутки времени, то формулу можно записать без дополнительного индекса нумерации платежей 

В этих формулах время измеряется в единицах периода ставки дисконтирования i. Обычно ставка даётся годовая, а время может быть дано в днях, месяцах, кварталах и т. д. В этом случае в качестве времени используют отношение времени в заданных единицах к продолжительности года в тех же единицах (например, если выплата через квартал, то это 0,25 года). Если платежи осуществляются через равные промежутки времени, пересчитывают ставку на этот период по формуле сложных процентов: 
Пример[править | править код]
Имеется облигация номиналом в 1000 рублей со сроком до погашения 1 год и ежеквартальным купоном 20 рублей, что соответствует купонной ставке 8 % годовых (20 x 4 / 1000 = 0,08). Владелец облигации получает в первые три квартала по 20 рублей, а в четвёртом квартале — 20 рублей и сумму погашения. Таким образом, структура выплат следующая: 20 + 20 + 20 + 1020. Периоды между платежами равные.
Теперь продисконтируем данный поток платежей. Допустим, ставка дисконтирования равна 6,14 % годовых (например, это ожидаемая инфляция или 5,5 % безрисковая ставка плюс премия за риск 0,64 % для инструментов с данным риском — цифра условная для примера). Можно посчитать квартальную ставку как 

То же самое можно рассчитать непосредственно через годовую ставку, не рассчитывая квартальную ставку, а используя время в долях от года:

Дисконтированная стоимость некоторых денежных потоков[править | править код]
Дисконтированная стоимость аннуитета[править | править код]
Если поток платежей аннуитетный, то есть платежи имеют одинаковую величину и выплачиваются через равные промежутки времени, то эта формула принимает вид (исходя из известной формулы суммы геометрической прогрессии):
,
где 




Дисконтированная стоимость вечных аннуитетов (перпетуитетов)[править | править код]
Для вечного аннуитета, то есть при бесконечно большом 
Дисконтированная стоимость платежей с постоянным темпом роста[править | править код]
Если платежи растут с постоянным темпом прироста g, то их дисконтированная стоимость вычисляется по формуле:
,
где 


В пределе (при бесконечно большом n) при 
Связанные понятия[править | править код]
- Чистый дисконтированный доход (ЧДД) или чистая дисконтированная (приведённая, текущая) стоимость (Net Present Value, NPV) — дисконтированная стоимость будущих доходов от инвестиционного проекта за минусом (дисконтированной) стоимости вложений в проект. Характеризует эффективность инвестиционного проекта и является одним из критериев выбора инвестиционных проектов.
См. также[править | править код]
- Дисконтированный срок окупаемости
Примечания[править | править код]
Литература[править | править код]
- Ширяев А. Н. Основы стохастической финансовой математики. — М.: ФАЗИС, 1998. — Т. 1. Факты. Модели. — 512 с. — ISBN 5-7036-0043-X.
Передача векселедержателями банковским структурам до наступления момента полного погашения ценной бумаги.
Кредитная организация выплачивает сумму по векселю за минусом комиссии (дисконта), соответствующего заранее определенным размерам.
Экономический смысл
Расчеты векселями — удобный способ платежа. Фирма, у которой недостаточно денежных средств для расчета по обязательствам, может выдать кредитору ценную бумагу. Ее оформление, в отличие от традиционных инвестиционных инструментов, не требует составления проекта эмиссии, длительного утверждения или регистрации в контролирующих органах: достаточно получить согласие кредитора и заполнить специальный бланк.
На практике случается, что векселедержателю требуются наличные деньги раньше, чем он может истребовать их по условиям векселя. Чтобы получить средства по ценной бумаге, он вправе обратиться в банк или другую компанию, которая выдаст ему часть суммы долга за минусом собственной комиссии. Эта операция носит название дисконтирования.
Ставка дисконта, используемая банками, аналогична той, что используется финансовыми структурами при выдаче ссуд юридическим лицам. Фактически, дисконтирование — это предоставление кредита владельцу ценной бумаги.
К банку, погасившему вексель, переходят права требования суммы долга с векселедателя и процентов по нему. Он не может продать ценную бумагу, потому что де-юре ее собственником остается уступивший свои права требования векселедержатель.
Векселедатель, к которому обратится банк в обозначенные сроки за погашением векселя, не вправе ставить под сомнение легитимность его требования. Если он считает, что сделка по дисконтированию была совершена с нарушением норм законодательства, он обязан доказать свою правоту в судебном порядке.
Порядок дисконтирования векселей
С точки зрения способа обозначения дохода держателя векселя бывают двух видов:
- Дисконтные. В них указывается твердая сумма, подлежащая выплате векселедержателю. Его доход — это разница между размером погашения ценной бумаги и стоимостью ее приобретения.
- Процентные. В них прописывается процентная ставка, по которой рассчитывается доход векселедержателя. Проценты начинают начисляться со дня, следующего за датой выдачи векселя, и прекращают «капать» в момент его полного погашения.
Для дисконтирования векселей, где указана твердая сумма долга, используется следующая формула:
ДВ = НВ* (1-ЧД* С)
где:
- ДВ — стоимость ценной бумаги, которую владельцу выплатит банк при ее досрочном погашении;
- НВ — номинальная стоимость векселя, указанная на ценной бумаге;
- ЧД — число дней, оставшееся до момента погашения, т.е. до даты, прописанной в векселе;
- С — ставка дисконтирования, объявленная кредитной организацией, т.е. плата, взимая ею за оказанные векселедержателю услуги.
Разница между НВ и ДВ — это сумма вознаграждения, отходящего банку за выполнение посреднических функций. Для процентных векселей используется более сложная формула дисконтирования:
ДВ = НВ* (1-ЧД* С)* (1+ ПО* СВ)
где:
- СВ — ставка процентов, указанная на векселе;
- ПО — период обращения ценной бумаги (в днях) до момента ее учета в банке.
Когда векселедержатель погашает вексель в кредитном учреждении раньше срока платежа, он автоматически теряет часть процентов по ценной бумаге, которые отходят в качестве вознаграждения банковской структуре.






