Дисконтированная (приведённая, текущая) стоимость — оценка стоимости (текущий денежный эквивалент) будущего потока платежей исходя из различной стоимости денег, полученных в разные моменты времени (концепция временно́й ценности денег). Денежная сумма, полученная сегодня, обычно имеет более высокую стоимость, чем та же сумма, полученная в будущем. Это связано с тем, что деньги, полученные сегодня, могут принести в будущем доход после их инвестирования. Кроме того, деньги полученные в будущем в условиях инфляции обесцениваются (на ту же сумму в будущем можно приобрести меньшее количество товаров и услуг). Также есть другие факторы, снижающие стоимость будущих платежей. Неравноценность разновременных денежных сумм численно выражается в ставке дисконтирования.
Дисконтированная стоимость некоторой будущей суммы 

Дисконтированная стоимость широко используется в экономике и финансах как инструмент сравнения потоков платежей, получаемых в разные сроки. Модель дисконтированной стоимости позволяет определить, какой объём финансовых вложений готов сделать инвестор для получения данного денежного потока. Дисконтированная стоимость будущего потока платежей является функцией ставки дисконтирования, которая может определяться в зависимости от:
- доходности альтернативных вложений;
- стоимости привлечения (заимствования) средств;
- инфляции;
- срока, через который ожидается будущий поток платежей;
- риска, связанного с данным будущим потоком платежей;
- других факторов.
Показатель дисконтированной стоимости используется в качестве основы для вычисления амортизации финансовых заимствований.
Практическое объяснение[править | править код]
Ценность денежных средств изменяется со временем. 100 рублей, полученные через пять лет, имеют иную (в большинстве случаев, меньшую) ценность чем 100 рублей, которые имеются в наличии. Имеющиеся в наличии денежные средства можно инвестировать в банковский депозит или любой другой инвестиционный инструмент, что обеспечит процентный доход. То есть 100 руб. сегодня, дают 100 руб. плюс процентный доход через пять лет. Кроме того, на имеющиеся в наличии 100 руб. можно приобрести товар, который через пять лет будет иметь более высокую цену вследствие инфляции. Следовательно 100 руб. через пять лет не позволят приобрести тот же товар. В данном примере показатель дисконтированной стоимости позволяет вычислить сколько на сегодняшний день стоят 100 руб., которые будут получены через пять лет.
Наращение процентов и дисконтирование[править | править код]
Пусть некоторая денежная сумма 



Соответственно, если дана денежная сумма 




Величину 


В общем случае сумма может быть приведена к любому моменту времени (не только к текущему):

Приведение разновременных сумм к одному и тому же моменту времени делает их сопоставимыми (равноценными) с точки зрения концепции временно́й ценности денег. Предполагается, что существует возможность вложить любую сумму в любой момент времени в некоторый инструмент (например, банковский депозит) с доходностью 


Пример[править | править код]
Если через 1 год ожидается сумма 121 рубль, то при ставке дисконтирования 10 % годовых дисконтированная стоимость будет равна 

В табличных процессорах в состав финансовых функций входит функция для вычисления дисконтированной стоимости. В OpenOffice.org Calc для вычисления дисконтированной стоимости различных видов платежей применяется функция PV.
Дисконтированная стоимость денежных потоков[править | править код]
Денежные потоки[править | править код]
Денежным потоком называют распределённое во времени движение денежных средств. Во многих случаях (депозиты, кредиты, ценные бумаги и др.) денежный поток представляет собой упорядоченную по времени совокупность денежных сумм (платежей) — это так называемый дискретный денежный поток или поток платежей. Таким образом, поток платежей 



В некоторых случаях частота платежей может быть настолько большой, что денежный поток можно считать непрерывным. В частности, это имеет место для денежных потоков от обычной операционной деятельности компаний, потоков от инвестиционных проектов и т. д. Формально для непрерывных потоков можно ввести функцию плотности потока 

Таким образом, можно считать, что денежный поток CF задаётся всегда упорядоченной совокупностью денежных сумм 
Дисконтированная стоимость потока платежей[править | править код]
Дисконтированная стоимость потока платежей 



Вывод формулы
Поток платежей разобьём на первый 






Аналогичным образом можно разделить остаточный поток на платёж 


Подставив это в первую формулу получим

Поступая аналогичным образом и далее до последнего платежа, окончательно получим формулу дисконтированной стоимости всего денежного потока

Интерпретация
При вложении суммы 



Таким образом, эта сумма равна сумме, которая будет получена в этот же момент, если последовательно под ту же ставку вкладывать отдельные элементы потока до времени t. Таким образом, дисконтированная стоимость денежного потока равна дисконтированной стоимости наращенной суммы этого потока.
Если платежи осуществляются через равные промежутки времени, то формулу можно записать без дополнительного индекса нумерации платежей 

В этих формулах время измеряется в единицах периода ставки дисконтирования i. Обычно ставка даётся годовая, а время может быть дано в днях, месяцах, кварталах и т. д. В этом случае в качестве времени используют отношение времени в заданных единицах к продолжительности года в тех же единицах (например, если выплата через квартал, то это 0,25 года). Если платежи осуществляются через равные промежутки времени, пересчитывают ставку на этот период по формуле сложных процентов: 
Пример[править | править код]
Имеется облигация номиналом в 1000 рублей со сроком до погашения 1 год и ежеквартальным купоном 20 рублей, что соответствует купонной ставке 8 % годовых (20 x 4 / 1000 = 0,08). Владелец облигации получает в первые три квартала по 20 рублей, а в четвёртом квартале — 20 рублей и сумму погашения. Таким образом, структура выплат следующая: 20 + 20 + 20 + 1020. Периоды между платежами равные.
Теперь продисконтируем данный поток платежей. Допустим, ставка дисконтирования равна 6,14 % годовых (например, это ожидаемая инфляция или 5,5 % безрисковая ставка плюс премия за риск 0,64 % для инструментов с данным риском — цифра условная для примера). Можно посчитать квартальную ставку как 

То же самое можно рассчитать непосредственно через годовую ставку, не рассчитывая квартальную ставку, а используя время в долях от года:

Дисконтированная стоимость некоторых денежных потоков[править | править код]
Дисконтированная стоимость аннуитета[править | править код]
Если поток платежей аннуитетный, то есть платежи имеют одинаковую величину и выплачиваются через равные промежутки времени, то эта формула принимает вид (исходя из известной формулы суммы геометрической прогрессии):
,
где 




Дисконтированная стоимость вечных аннуитетов (перпетуитетов)[править | править код]
Для вечного аннуитета, то есть при бесконечно большом 
Дисконтированная стоимость платежей с постоянным темпом роста[править | править код]
Если платежи растут с постоянным темпом прироста g, то их дисконтированная стоимость вычисляется по формуле:
,
где 


В пределе (при бесконечно большом n) при 
Связанные понятия[править | править код]
- Чистый дисконтированный доход (ЧДД) или чистая дисконтированная (приведённая, текущая) стоимость (Net Present Value, NPV) — дисконтированная стоимость будущих доходов от инвестиционного проекта за минусом (дисконтированной) стоимости вложений в проект. Характеризует эффективность инвестиционного проекта и является одним из критериев выбора инвестиционных проектов.
См. также[править | править код]
- Дисконтированный срок окупаемости
Примечания[править | править код]
Литература[править | править код]
- Ширяев А. Н. Основы стохастической финансовой математики. — М.: ФАЗИС, 1998. — Т. 1. Факты. Модели. — 512 с. — ISBN 5-7036-0043-X.
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Что такое ставка дисконтирования, для чего она нужна и как ее рассчитывать. Рассказываем об этом в нашем обзоре

В этой статье вы узнаете
- Что это
- Как появилась
- Как рассчитать
- Интуитивные методы определения ставки
- Модели расчета на основе премий за риск
- Аналитические методы расчета
- Как применяется
Что такое ставка дисконтирования
Ставка дисконтирования — это эталонная величина, выраженная в процентах, применяемая для сравнительной оценки эффективности инвестиций.
Например, вам нужно выбрать: положить деньги в банк со ставкой депозита 12% сроком на пять лет с ежегодной выплатой процента или купить
облигации
с погашением через девять лет с купоном 8,5%, выплачиваемым дважды в год и с текущей ценой 91% от номинала. Как вы будете выбирать, да еще учитывая, что уровень инфляции составляет около 8%?

Аналитик занимается оценкой стоимости
(Фото: Shutterstock)
Для решения этих задач используется прием, который называют дисконтированием. С помощью дисконтирования можно сопоставить будущие денежные потоки и выбрать из нескольких вариантов инвестиций самый выгодный. А ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.
Правильный расчет ставки дисконтирования позволит вам:
- оценить эффективность инвестиций относительно надежных вкладов;
- сравнить варианты инвестиций с разной длительностью вложения;
- сравнивать доходность вложений инструментов с разной степенью риска.
Ставка дисконтирования зависит от множества факторов: уровень инфляции, доступные для инвестора варианты вложений, риск вложений, стоимость вашего капитала и др. Но далеко не все внешние факторы можно достоверно учесть в ставке.
Как появилась ставка дисконтирования
Первоначально ставка дисконтирования применялась при учете векселей. Принимая к оплате вексель, банкиры знали сумму, которую они получат, когда предъявят вексель к погашению. Но чтобы им самим заработать, банкиры выплачивали предъявителю деньги со скидкой — дисконтом. А процентная ставка, в которой измерялся их доход, называлась учетной ставкой, или ставкой дисконтирования (discount rate). Сумма, которая выплачивалась предъявителю векселя, рассчитывалась как раз с помощью дисконтирования — зная, сколько он получит в будущем и учитывая текущий уровень процентных ставок, банкир определял текущую стоимость денег.
Этот прием оказался настолько универсальным и полезным, что стал широко применяться при оценке и сравнении эффективности вложений в разные инструменты или проекты. При дисконтировании инвестор, как и банкир при учете векселей, пересчитывает стоимость денег, которые он получит в будущем, причем в совершенно разные сроки, на текущую стоимость. Он как бы проецирует стоимость денег из будущего на плоскость настоящего времени. А центральным звеном расчетов выступает ставка дисконтирования.

Как рассчитать ставку дисконтирования
При расчете ставки дисконтирования очень важно определить ставку, которая позволит максимально корректно привести будущую стоимость доходов и расходов к текущей. Для этого нужно учитывать и общий уровень процентных ставок, и факторы риска вложений в отдельные инструменты.
При расчете ставки дисконтирования нужно учесть два основных вида факторов:
- Уровень безрисковых ставок.
- Премии за риск.
Безрисковые ставки — это процентные ставки инструментов с минимальным для инвестора уровнем риска. Обычно такими инструментами являются облигации центрального правительства — ОФЗ в России, US Treasuries в США и т. п. Также в качестве безрисковых ставок могут учитываться ставки по депозитам системообразующих банков. Иногда как безрисковая ставка может рассматриваться ключевая ставка центральных банков.
Уровень безрисковых ставок является фундаментальным — он определяет минимальный уровень всех ставок дисконтирования.
Премии за риск — это надбавки к уровню безрисковых ставок, которые стоит учитывать при вложении в отдельные инструменты или проекты. Это могут быть общие факторы — уровень инфляции, надбавка за страновой риск; факторы, учитывающие риск вложения в отдельные инструменты, — надбавка за отраслевой риск, надбавка за индивидуальный риск (зависит от надежности эмитента, инструмента или проекта).
Учет премий за риск позволит более точно настроить инструмент дисконтирования, чтобы избежать ошибок в сравнении разных инвестиций.
При расчете ставки дисконтирования используются различные способы и методы, которые можно объединить в такие основные группы:
- интуитивные методы;
- модели на основе премий за риск;
- аналитические модели.
Интуитивные методы
В эту группу включается:
- собственно интуитивный метод.
- экспертный метод.
Интуитивный метод — это способ определения ставки дисконтирования на основе субъективного видения инвестора. Проще говоря, когда инвестор прикидывает ставку дисконтирования практически на глазок. Например, он рассуждает так: «Я могу положить деньги на депозит в надежном банке под 12–15%. Тогда эффективность других вложений я буду сравнивать с таким уровнем ставок».
Экспертный метод — это, по сути, тот же интуитивный метод, только итоговая величина ставки дисконтирования выводится как совокупный консенсус нескольких экспертов с тем или иным уровнем обоснованности их мнений.

Аналитики совещаются
(Фото: Shutterstock)
Модели на основе премий за риск
К моделям на основе премий за риск относятся, например, такие модели, как:
- модель кумулятивного построения;
- модель капитальных активов CAPM.
Общим для этих моделей является то, что ставка дисконтирования выводится как сумма безрисковой ставки и премий за риск.
Модели кумулятивного построения — это метод определения ставки дисконтирования, при котором к безрисковой процентной ставке прибавляются все премии за риск, которые можно определить для конкретного инструмента.
Формула расчета ставки дисконтирования кумулятивным способом выглядит так:
![]()
где r0 — безрисковая ставка,
r1, r2, rn — все премии за риск для оцениваемого инструмента.
Модель капитальных активов CAPM (Capital Asset Pricing Model, модель оценки капитальных активов) — это метод определения ставки дисконтирования для сравнительной оценки эффективности вложений в акции, при котором к безрисковой процентной ставке прибавляется премия за риск по отдельному инструменту с учетом его β-коэффициента.
β-коэффициент (бета-коэффициент) — это мера рыночного риска акции, которая показывает изменчивость доходности акции к доходности на рынке в среднем. β-коэффициент численно показывает, на сколько процентов изменяется цена акции бумаги при росте или снижении индекса на 1%. Положительный коэффициент говорит о том, что акция двигается в одном направлении с рынком, а отрицательный коэффициент означает, что акция двигается в противоположную от общего направления рынка сторону.
β-коэффициенты рассчитываются и публикуются и аналитиками, и торговыми площадками, например Московской биржей.
Формула расчета ставки дисконтирования по CAPM выглядит так:
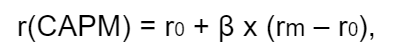
где r0 — безрисковая ставка,
β — β-коэффициент,
rf — средняя доходность фондового рынка (биржевого индекса).

Аналитические диаграммы
(Фото: Shutterstock)
Аналитические методы
Аналитические методы — способы расчета ставки дисконтирования с применением элементов финансового анализа. Среди аналитических методов можно выделить:
- WACC;
- мультипликативные методы.
WACC — это средневзвешенная стоимость капитала (Weighted Average Cost of Capital). WACC используется компаниями для сравнительной оценки эффективности инвестиционных проектов.
Как правило, у компании есть два вида используемого капитала — собственный и заемный. Собственный капитал равен сумме средств, принадлежащих самой компании или причитающихся ее акционерам. Заемный капитал — это средства, привлеченные компанией извне (кредиты и займы). Заемный капитал достается компании не бесплатно — по кредитам и займам она должна платить проценты.
В случае когда у компании или у инвестора только заемные деньги, то для них самым главным становится то, чтобы инвестиционные проекты приносили больше, чем приходится платить по кредиту. В этом случае при оценке инвестиционных проектов в качестве ставки дисконтирования можно использовать ставку по кредиту, скорректированную на ставку налога на прибыль.
Но когда у компании есть и собственный, и заемный капитал, то ставка дисконтирования по модели WACC считается следующим образом:
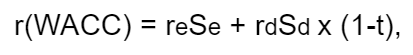
где re — стоимость собственного капитала,
Se — доля собственного капитала,
rd — стоимость заемного капитала,
Sd — доля заемного капитала,
t — ставка налога на прибыль.
Стоимость заемного капитала rd — это средневзвешенный процент по имеющимся займам и кредитам.
Стоимость собственного капитала re может определяться либо методом CAPM, описанным выше, либо другим способом — например, с помощью модели Гордона.
Модель Гордона для оценки стоимости собственного капитала компании предполагает, что за возможность использования собственного капитала компания платит дивидендами. Значит, стоимость собственного капитала определяется отношением суммы выплаченных дивидендов к сумме денег, привлеченных в ходе размещения акций.
В итоге формула, по которой рассчитывается стоимость собственного капитала по Гордону, выглядит так:
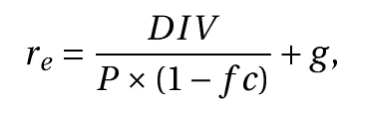
где DIV — это сумма годовых ожидаемых дивидендов на одну акцию;
P — цена размещения акций,
fc — затраты на эмиссию (в %),
g — темпы прироста дивидендов.
Мультипликативные методы — это способы расчета ставки дисконтирования на основе различных коэффициентов прироста и других коэффициентов предприятий.
Это может быть, например:
- расчет ставки на основе рентабельности капитала (ROE), когда за ставку дисконтирования принимают показатель ROE;
- расчет ставки на основе рентабельности активов (ROA), когда за ставку дисконтирования принимают показатель ROA;
- расчет ставки на основе рыночных мультипликаторов, когда за ставку дисконтирования принимают значение доходности как отношения прогнозного дохода к текущей рыночной стоимости компании. Например, прогнозное значение чистой прибыли на акцию (EPS) к рыночной стоимости акций или прогнозное значение денежного потока к капитализации

Как применяется ставка дисконтирования
Как мы писали вначале, ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.
Дисконтирование — это приведение будущей стоимости денежных потоков к стоимости в настоящее время по ставке дисконтирования.
Один из частых результатов дисконтирования — получение чистой текущей (приведенной) стоимости денег.
Чистая текущая стоимость (NPV, Net Present Value) — разница между всеми денежными притоками и оттоками, приведенными к текущему моменту времени по ставке дисконтирования. Эта величина показывает сумму денежных средств, которую инвестор ожидает получить от проекта, пересчитанную к настоящему времени.
Сравнив NPV разных по длительности инвестиционных вариантов, инвестор может выбрать наиболее доходный.
Узнайте о возможностях нашего Каталога в телеграм-канале «РБК Инвестиций»
Долговая ценная бумага, владелец которой имеет право получить от выпустившего облигацию лица, ее номинальную стоимость в оговоренный срок. Помимо этого облигация предполагает право владельца получать процент от ее номинальной стоимости либо иные имущественные права.
Облигации являются эквивалентом займа и по своему принципу схожи с процессом кредитования. Выпускать облигации могут как государства, так и частные компании.
Ставка дисконтирования: суть и методы расчета
Оценка инвестиционных проектов производится с помощью дисконтирования. О том, что это такое и каким образом рассчитывается эта ставка, — в статье.

В основе дисконтирования лежит фундаментальный экономический закон. Он заключается в постоянном снижении покупательной способности денег с течением времени. Скорость падения стоимости денег зависит от ставки дисконтирования, которая для каждого конкретного проекта индивидуальна.
- Как выглядит формула дисконтирования
- В поиске консенсуса
- Метод расчета WACC
- Модель оценки капитальных активов CAPM
- Метод кумулятивного построения рисков
- Другие модели расчета
- Кратко
Как выглядит формула дисконтирования
Формула дисконтирования представляет собой деление будущей денежной суммы на фактор снижения стоимости денег:

Таким образом, чем выше ставка дисконтирования, тем ниже оказывается стоимость будущих денег, приведенная к настоящему моменту времени. Как следствие, ниже рентабельность инвестиционного проекта и длиннее срок окупаемости вложений. При этом чем больше рисков у проекта, тем меньше желающих в него инвестировать и тем дороже цена привлеченного капитала, а значит, и выше ставка дисконтирования.
Если будущий доход — определенная инвестором целевая величина, то чему должна быть равна ставка дисконтирования — большой вопрос. В любом случае ее значение должно быть достаточным, чтобы учитывать размер инфляции и совокупность рисков.
Существует несколько способов расчета ставки дисконтирования, остановимся на основных методах и моделях.
В поиске консенсуса
Методы экспертных оценок основаны на опыте и интуиции специалистов, привлеченных для расчета ставки дисконтирования. В простейшем случае таким специалистом будет один человек, и это сам инвестор. Он определяет величину ставки дисконтирования для конкретного объекта вложений на основе собственного опыта и представлений о рисках и трендах рынка.
Однако, если дело касается крупных проектов, к оценке привлекают нескольких профессиональных экспертов, чаще всего специализирующихся на отдельных областях знаний: рисках, фондовом рынке, строительстве, технологиях и прочем. В этом случае организуют либо очное обсуждение величины ставки дисконтирования, либо проводят заочный опрос экспертов. В итоге ставка дисконтирования определяется либо в результате консенсуса экспертов, либо как средняя величина полученных экспертных оценок.
Эксперты учитывают множество факторов, влияющих на величину ставки дисконтирования, в числе которых:
- размер компании и стадия ее жизненного цикла;
- ликвидность акций компании, их волатильность;
- финансовое состояние и кредитный рейтинг;
- деловая репутация компании;
- отрасль, в которой работает компания, и присущие этой отрасли риски;
- инфляционные ожидания;
- страновые риски и другие факторы.
Нередко эксперты обсуждают даже не величину ставки дисконтирования, а поправочный коэффициент, на который умножается безрисковая ставка, в роли которой выступает доходность по ценным бумагам, эмитированным государством. Такими активами в России являются облигации федерального займа (ОФЗ).
Заметим, что безрисковая ставка сама по себе подвержена изменениям. В самом обычном случае она зависит от политики центрального банка, который регулирует рынок с помощью величины учетной ставки, изменяющейся достаточно плавно. Однако при наступлении чрезвычайных событий в экономике безрисковая ставка может изменяться кардинально.
Следует учесть, что качество результатов, полученных методами экспертных оценок, всегда будет страдать от субъективности оценок специалистов. Поэтому проверку валидности оценки ставки дисконтирования обычно проводят с помощью количественных методов.
Метод расчета WACC
Классический метод расчета ставки дисконтирования носит название средневзвешенной стоимости совокупного капитала фирмы (Weighted Average Cost of Capital, WACC). Он учитывает, что капитал фирмы состоит из капитала акционеров и заемных средств. Экономический смысл метода WACC заключается в том, что доходы компании должны превышать затраты на капитал.
Формула расчета по методу WACC выглядит следующим образом:

Стоимость заемного капитала снижается на величину налога на прибыль, поскольку проценты по внешнему долгу относятся на себестоимость согласно ст. 265 НК РФ, в то время как налогового вычета в отношении собственного капитала нет.
Величины доли собственного и заемного капитала вычисляются на основе баланса компании или годовых отчетов акционерных обществ, при условии если они публикуются. Ставку по заемным средствам можно определить на основе информации Банка России по долгосрочным кредитам свыше трех лет. А вот величину процентов за пользование собственным капиталом можно рассчитать либо с помощью метода CAPM, или метода Гордона (об этом читайте ниже), либо методом экспертных оценок.
Расчет по модели WACC может быть осложнен из-за отсутствия доступных данных о финансовом состоянии компании. Кроме того, данная модель не учитывает риски, которые могут проявиться в будущем.
Модель оценки капитальных активов CAPM
Модель CAPM (Capital Asset Pricing Model) была предложена независимо друг от друга несколькими группами ученых в 1960-х годах для оценки доходности инвестирования в акции или собственный капитал компаний. Таким образом, CAPM можно применять как для расчета доходности собственного капитала в модели WACC, так и в качестве определения ставки дисконтирования при вложениях в акции.
В упрощенном виде формула представляет собой сумму:

Второе слагаемое характеризует премию за риск, при этом rf представляет собой ожидаемую ставку доходности акций, а коэффициент β характеризует чувствительность оцениваемой акции к изменениям средней рыночной доходности. Его величина показывает, на сколько процентов изменится цена акции при росте или снижении стоимости портфеля акций на 1%. Если β — положительная величина, то движения цены акций будут синхронизированы с рынком. При отрицательных β изменения цены акций происходят против движения цен рынка.
Расчеты коэффициентов β для крупных эмитентов публикуют аналитические компании и биржи. Для компаний, чьи акции котируются на бирже, но для которых коэффициент β не опубликован, его можно рассчитать на основе статистических данных о торгах. Для непубличных компаний премию за риск определяют на основе экспертных оценок.
Существует несколько популярных модификаций модели CAPM, которые учитывают различные виды рисков.
Ученые Ю. Фама и К. Френч обнаружили, что доходность акций компаний с малой капитализацией выше среднерыночных показателей, а кроме того, рост стоимости акций зависит от отношения балансовой стоимости акционерного капитала компании к его рыночной стоимости. Они предложили трехфакторную модель CAPM, добавив в классическую формулу поправки на размер компании и ее финансовое состояние.
М. Кархарт пошел еще дальше и предложил четырехфакторную модель CAPM. Дополнительный параметр характеризует скорость изменения цены акций.
Метод кумулятивного построения рисков
В этих моделях безрисковая ставка и величина инфляции суммируются с отдельными рисковыми премиями для рассматриваемой компании или инвестиционного инструмента.
Например, согласно методике компании Альт-Инвест, премия за риск при расширении производства должна составлять 3%, а если компания выходит на новые рынки — 6%, создает новый продукт — 9%, если приступает к проекту в новой для себя отрасли — 12%.
Исследователи П. Л. Виленский, В. Н. Лившиц и С. А. Смоляк предложили к безрисковой ставке добавлять премию за риск, зависящую от проведения исследовательских работ, применяемых технологий, внешней среды, цикличности производства. Премии за риск могут достигать 47%.
Также в свое время правительство России разработало «Положение об оценке эффективности инвестиционных проектов при размещении на конкурсной основе централизованных инвестиционных ресурсов бюджета развития Российской Федерации» (утверждено Постановлением Правительства РФ №1470 от 22.11.1997), в котором рисковая премия зависела от типа проекта. В частности, инвестиции при интенсификации производства на базе освоенной техники добавляют к безрисковой ставке 3–5%, а вложения в исследования и инновации — 18–20%.
Другие модели расчета
Модель постоянного роста М. Дж. Гордона применима для предприятий, регулярно выплачивающих дивиденды. Она предполагает, что дивиденды будут расти в будущем с одинаковым темпом роста, что, безусловно, ограничивает область применения модели.
Метод расчета ставки дисконтирования на основе рентабельности капитала может применяться для компаний, акции которых не котируются на фондовом рынке. Для оценки ставки дисконтирования могут применяться различные показатели: рентабельности собственного капитала, рентабельности активов и другие. Однако следует принять во внимание, что оценка инвестиционных проектов в данном случае будет происходить по историческим данным, что не совсем надежно.
Кратко
-
1
Оценка инвестиционных проектов производится с помощью дисконтирования — приведения будущей стоимости к настоящему моменту времени. Скорость падения стоимости денег зависит от ставки дисконтирования, которая для каждого конкретного проекта индивидуальна. -
2
Методы экспертных оценок основаны на опыте и интуиции специалистов, привлеченных для расчета ставки дисконтирования. Качество результатов всегда будет страдать от субъективности оценок специалистов. -
3
Метод средневзвешенной стоимости совокупного капитала фирмы (Weighted Average Cost of Capital, WACC) учитывает стоимость владения собственным и заемным капиталом, но не учитывает риски. -
4
Метод CAPM можно применять как для расчета доходности собственного капитала в модели WACC, так и в качестве определения ставки дисконтирования при вложениях в акции. -
5
В моделях кумулятивного построения рисков безрисковая ставка и величина инфляции суммируются с отдельными рисковыми премиями. -
6
Другие модели, в частности модель постоянного роста М. Дж. Гордона и расчет ставки дисконтирования на основе рентабельности капитала, имеют ограничения.
Данный справочный и аналитический материал подготовлен компанией ООО «Ньютон Инвестиции» исключительно в информационных целях. Оценки, прогнозы в отношении финансовых инструментов, изменении их стоимости являются выражением мнения, сформированного в результате аналитических исследований сотрудников ООО «Ньютон Инвестиции», не являются и не могут толковаться в качестве гарантий или обещаний получения дохода от инвестирования в упомянутые финансовые инструменты. Не является рекламой ценных бумаг. Не является индивидуальной инвестиционной рекомендацией и предложением финансовых инструментов. Несмотря на всю тщательность подготовки информационных материалов, ООО «Ньютон Инвестиции» не гарантирует и не несет ответственности за их точность, полноту и достоверность.
Читайте также
Общество с ограниченной ответственностью «Ньютон Инвестиции» осуществляет деятельность на
основании лицензии профессионального участника рынка ценных бумаг на осуществление
брокерской деятельности №045-14007-100000, выданной Банком России 25.01.2017, а также
лицензии на осуществление дилерской деятельности №045-14084-010000, лицензии на
осуществление деятельности по управлению ценными бумагами №045-14085-001000 и лицензии
на осуществление депозитарной деятельности №045-14086-000100, выданных Банком России
08.04.2020. ООО «Ньютон Инвестиции» не гарантирует доход, на который рассчитывает инвестор,
при условии использования предоставленной информации для принятия инвестиционных
решений. Представленная информация не является индивидуальной инвестиционной
рекомендацией. Во всех случаях решение о выборе финансового инструмента либо совершении
операции принимается инвестором самостоятельно. ООО «Ньютон Инвестиции» не несёт
ответственности за возможные убытки инвестора в случае совершения операций либо
инвестирования в финансовые инструменты, упомянутые в представленной информации.
С целью оптимизации работы нашего веб-сайта и его постоянного обновления ООО «Ньютон
Инвестиции» используют Cookies (куки-файлы), а также сервис Яндекс.Метрика для
статистического анализа данных о посещениях настоящего веб-сайта. Продолжая использовать
наш веб-сайт, вы соглашаетесь на использование куки-файлов, указанного сервиса и на
обработку своих персональных данных в соответствии с «Политикой конфиденциальности» в
отношении обработки персональных данных на сайте, а также с реализуемыми ООО «Ньютон
Инвестиции» требованиями к защите персональных данных обрабатываемых на нашем сайте.
Куки-файлы — это небольшие файлы, которые сохраняются на жестком диске вашего
устройства. Они облегчают навигацию и делают посещение сайта более удобным. Если вы не
хотите использовать куки-файлы, измените настройки браузера.
Условия обслуживания могут быть изменены брокером в одностороннем порядке в любое время в соответствии с условиями
регламента брокерского обслуживания. Клиент обязан самостоятельно обращаться на
сайт брокера
за сведениями об изменениях, произведенных в регламенте
брокерского обслуживания и несет все риски в полном объеме, связанные с неполучением или несвоевременным получением
сведений в результате неисполнения или ненадлежащего исполнения указанной обязанности.
© 2023 Ньютон Инвестиции
Метод дисконтирования основан на известном экономическом законе, который заключается в убывающей стоимости денег. Деньги со временем обесцениваются — это заметно даже тем, кто не знаком с экономической теорией. При растущих ценах реальная стоимость денег уменьшается, то есть на условные 1000 руб. завтра мы сможем купить меньше, чем сегодня, и меньше, чем вчера. Чтобы ответить на вопрос, сколько в будущем будут стоить сегодняшние 1000 руб., используется метод дисконтирования денежных потоков. Пример расчета и наглядное объяснение данного метода вы найдете в статье ниже.
Расчет дисконтированного денежного потока
Стоимость денег может изменяться не только под влиянием инфляции, но и за счет других факторов. Например, деньги в форме депозита в банке могут принести прибыль, а при выдаче денег в кредит всегда существует риск недополучения предполагаемой возвратной суммы. Точка отсчета в методе дисконтирования — настоящий момент. Именно на текущую дату определяется стоимость будущих денежных потоков.
Дисконтирование денежных потоков— это приведение размера денежных средств, полученных в разные интервалы времени в соответствие с их реальной стоимостью на текущий момент. Метод применяется при оценке бизнеса и анализе экономической эффективности инвестиционных проектов, расчете их окупаемости и составлении бизнес-планов. Рассчитывая экономическую целесообразность будущего бизнес-проекта, инвестор приводит в соответствие планируемый объем будущих денежных потоков к их текущей реальной стоимости.
Формулы сложных процентов и дисконтирования
Смысл операции дисконтирования легко объяснить на небольшом примере. Например, в наличии сумма S0 = 1000 руб. Если положить эту сумму в банк под 7% годовых с ежегодной капитализацией процентов, т.е. зачислением их во вклад в конце года, мы получим через год:
S1 =1000 + 0,07 х 1000 = (1 + 0,07) х 1000 = 1070 руб.
Через 2 года: S2 = (1 + 0,07) х (1 + 0,07) х 1000 = (1+ 0,07)2 х 1000 = 1144,90 руб.
Через 3 года: S3 = (1+0,07)3 х 1000 = 1225,04 руб.
Через n-лет: Sn = (1+0,07)n х 1000, и таким образом формула сложных процентов выглядит так:
Sn = (1+P)n х S0, где
Sn — сумма денег через n-периодов начисления процентов;
S0 — первоначальная сумма денег;
P — процентная ставка по депозиту за период.
Подведем итог: при размещении денег на депозите сумма в размере 1000 руб., которая имеется в наличии сейчас, будет равняться по стоимости 1070 рублям, полученным через 1 год, и сумме 1225,04 руб., выплаченной через 3 года и т. д.
Расчет дисконтированного денежного потока – задание, обратное предыдущему: необходимо вычислить сумму S0 на текущий момент времени, равную по стоимости сумме Snчерез n-количество лет. Другими словами,величина Sn нам известна, нужно рассчитать S0.
Формула дисконтирования после простых математических преобразований расчета сложных процентов будет выглядеть так:
S0 = Sn / (1+P)n.
Величина P в этом расчете не процентная ставка, а ставка дисконтирования.
S0 — это продисконтированный денежный поток;
Sn — денежный поток каждого расчетного периода. Число n в формуле обозначает количество расчетных периодов, как правило, расчетным периодом в экономических расчетах считают год, иногда квартал или месяц.
Таким образом, если вернуться к предыдущему примеру, при ставке дисконтирования 7% деньги в сумме 1070 руб., выплаченные через 1 год, будут равняться 1000 руб. в настоящем: 1070 / (1+ 0,07) = 1000.
Инструменты дисконтирования: денежные потоки и ставка
В начале расчетов денежные потоки группируют в разрезе некоторых временных интервалов: год, квартал, месяц, а затем суммируют. Полученные величины могут быть с плюсом (поступления больше оттоков) или с минусом, убыточными (отток превышает сумму поступлений). В качестве денежного потока в расчетах могут считать:
-
чистый доход, равный поступившим доходам за вычетом расходов;
-
прибыль, рассчитываемая до исчисления налогов;
-
чистый поток наличности, из которого исключаются текущие затраты на содержание и реконструкцию объекта.
Вычисление ставки дисконтирования — наиболее ответственный момент в расчетах. В самом простом варианте, когда инвестор планирует разместить деньги на депозите, защитив их от инфляции, в качестве основы для расчета ставки применяют прогнозируемый индекс инфляции. Если кроме сбережения финансов планируется еще и получение дополнительной прибыли, то к ставке инфляции добавляется желаемый процент дохода. При инвестициях, особенно долгосрочных, необходимо учитывать не только инфляцию и норму ожидаемой прибыли, но различные сопутствующие риски. Поэтому в ставку дисконтирования закладываются еще и так называемые премии за риск, а при пользовании заемными средствами для реализации инвестиционного проекта к ставке добавляют еще процент по банковским кредитам, выпуску облигаций и т. п.
Чаще всего при анализе окупаемости дисконтная ставка складывается из безрисковой базовой доходности, приравненной к ключевой ставке ЦБ РФ или средневзвешенному проценту по банковским депозитам с добавлением премии за риск.
Дисконтирование денежных потоков: пример расчета
Проведем расчет дисконтированных денежных потоков для инвестиционных вложений сроком на 3 года. В нашем примере дисконтная ставка равна 15%, из них 8% — средневзвешенная ставка банковских депозитов и 7% — премия за риск. Период дисконтирования равен 1 году.
1. Выпишем для каждого годового периода ожидаемую сумму дохода и расходов в рублях. Будем считать, что расходы каждый год будут неизменными, а размер поступлений будет меняться.
2. Рассчитаем разность между доходами и расходами на каждый год.
Таблица расчета:
|
Период |
Доходы |
Расходы |
Чистый доход |
|
1 год |
80 000 |
90 000 |
-10 000 |
|
2 год |
120 000 |
90 000 |
+30 000 |
|
3 год |
150 000 |
90 000 |
+ 60 000 |
3. Приводим финансовые потоки в соответствие к текущему моменту, используя ставку дисконтирования 15%. Применяем коэффициент дисконтирования (1 + 0,15)n, дисконтирующий каждый поток, где n — число каждого года, для которого делаем расчет. Итак:
1 год: -10 000 / (1 + 0,15) = -8 695,65 руб.
2 год: +30 000 / (1 + 0,15)2 = 22 727,27 руб.
3 год: +60 000 / (1 + 0,15)3 = 39 473,68 руб.
4. Полученные суммы складываем:
-8 695,65 + 22 727,27 + 39 473,68 = 53 505,30 руб.
Сумма 53 505,30 – это дисконтированный денежный поток. Положительная величина свидетельствует о привлекательности данного проекта для инвесторов и возможности последующего анализа его перспективности.






