Решение уравнений с дробями

О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:


Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:


На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение: 
- Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение  .
.
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
 .
.
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
 .
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
 .
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
 .
.
 .
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
 .
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
 .
.
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:

Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
 .
.
 .
.
Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:
 ,
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
 .
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
 .
.
Общий знаменатель — выражение

Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:

Выполнив преобразования, придём к квадратному уравнению
 .
.
 .
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
 .
.
Решение. Введём новую переменную, обозначив  . Получим уравнение с переменной y :
. Получим уравнение с переменной y :
 .
.
Корни этого уравнения:

 или
или  .
.
Из уравнения  находим, что
находим, что
 .
.
Из уравнения  находим, что
находим, что
 .
.
Итак, данное уравнение имеет четыре корня:
 ,
,  .
.
Как решать квадратные уравнения? Дискриминант.
Поработаем с квадратными уравнениями. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:




Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:


Какие случаи возможны при использовании этой формулы? Всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!
Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:



Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:


Это неполные квадратные уравнения. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с.
Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0, или х = 4
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х = +3 и х = -3.
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
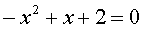
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Дробные уравнения. ОДЗ.
Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения. Или их ещё называют гораздо солиднее – дробные рациональные уравнения. Это одно и то же.
Дробные уравнения.
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе. Хотя бы в одном. Например:


Напомню, если в знаменателях только числа, это линейные уравнения.
Как решать дробные уравнения? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.
Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.
Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:

Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?
В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2). Умножаем:

Это обычное умножение дробей, но распишу подробно:

Обратите внимание, я пока не раскрываю скобку (х + 2)! Так, целиком, её и пишу:

В левой части сокращается целиком (х+2), а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:

А это уравнение уже решит всякий! х = 2.
Решим ещё один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2х = 2х/1, можно записать:

И опять избавляемся от того, что нам не очень нравится – от дробей.
Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2). А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:

Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.

С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!

А вот теперь уже раскрываем скобки:

Приводим подобные, переносим всё в левую часть и получаем:

Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:

Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3. Два корня.
Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым. Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет! При любом иксе получается неправда.
Осознали главный способ решения дробных уравнений? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.
Однако менять исходное выражение в нужную нам сторону надо по правилам, да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.
Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ! Но для начала посмотрим, попадаете вы в неё, или нет?
Разберём простой пример:

Дело уже знакомое, умножаем обе части на (х – 2), получаем:

Напоминаю, со скобками (х – 2) работаем как с одним, цельным выражением!

Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2 ничего нет, можно и не рисовать. Сокращаем:
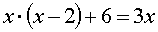
Раскрываем скобки, переносим всё влево, приводим подобные:

Решаем, проверяем, получаем два корня. х = 2 и х = 3. Отлично.
Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?
Если решите, что ответ 5, – вы попали в засаду. И задание вам не засчитают. Зря трудились… Правильный ответ 3.
В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный пример. И если при х = 3 у нас всё чудненько срастётся, получим 9 = 9, то при х = 2 получится деление на ноль! Чего делать нельзя категорически. Значит х = 2 решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3.
Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!
Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля. А х – 2 при х = 2 равно нулю! Так что всё честно.
И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!
Спокойно! Без паники!
В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ. Область Допустимых Значений.
источники:
http://function-x.ru/sq_fractional_equations.html
http://megalektsii.ru/s62947t7.html
Как найти дискриминант квадратного уравнения

О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, содержащее переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим:
13 = 12 — противоречие.
Значит, х = 5 не является корнем уравнения.
Если же х = 4, то при подстановке в уравнение мы получим:
12 = 12 — верное равенство.
Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.
Такое уравнение можно решить с помощью формулы дискриминанта.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Определим, чему равны коэффициенты a, b, c.
Вычислим значение дискриминанта по формуле D = b2 − 4ac.
Если дискриминант D 0, то у уравнения две корня, равные
Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x 2 – 4x + 2 = 0.
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 3 * 2 = 16 – 24 = -8.
Ответ: D 2 – 6x + 9 = 0.
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b 2 – 4ac = (-6) 2 – 4 * 1 * 9 = 36 – 36 = 0.
D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x 2 – 4x – 5 = 0.
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 1 * (-5) = 16 + 20 = 36.
D > 0, значит уравнение имеет два корня:
Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Как решать квадратные уравнения? Дискриминант.
Поработаем с квадратными уравнениями. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:




Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:


Какие случаи возможны при использовании этой формулы? Всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!
Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:



Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:


Это неполные квадратные уравнения. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с.
Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0, или х = 4
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х = +3 и х = -3.
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
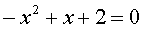
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось – надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий. Если в вашем уравнении есть дробные коэффициенты, – избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Дробные уравнения. ОДЗ.
Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения. Или их ещё называют гораздо солиднее – дробные рациональные уравнения. Это одно и то же.
Дробные уравнения.
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе. Хотя бы в одном. Например:


Напомню, если в знаменателях только числа, это линейные уравнения.
Как решать дробные уравнения? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.
Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.
Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:

Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?
В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2). Умножаем:

Это обычное умножение дробей, но распишу подробно:

Обратите внимание, я пока не раскрываю скобку (х + 2)! Так, целиком, её и пишу:

В левой части сокращается целиком (х+2), а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:

А это уравнение уже решит всякий! х = 2.
Решим ещё один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2х = 2х/1, можно записать:

И опять избавляемся от того, что нам не очень нравится – от дробей.
Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2). А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:

Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.

С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!

А вот теперь уже раскрываем скобки:

Приводим подобные, переносим всё в левую часть и получаем:

Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:

Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3. Два корня.
Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым. Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет! При любом иксе получается неправда.
Осознали главный способ решения дробных уравнений? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.
Однако менять исходное выражение в нужную нам сторону надо по правилам, да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.
Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ! Но для начала посмотрим, попадаете вы в неё, или нет?
Разберём простой пример:

Дело уже знакомое, умножаем обе части на (х – 2), получаем:

Напоминаю, со скобками (х – 2) работаем как с одним, цельным выражением!

Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2 ничего нет, можно и не рисовать. Сокращаем:
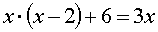
Раскрываем скобки, переносим всё влево, приводим подобные:

Решаем, проверяем, получаем два корня. х = 2 и х = 3. Отлично.
Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?
Если решите, что ответ 5, – вы попали в засаду. И задание вам не засчитают. Зря трудились… Правильный ответ 3.
В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный пример. И если при х = 3 у нас всё чудненько срастётся, получим 9 = 9, то при х = 2 получится деление на ноль! Чего делать нельзя категорически. Значит х = 2 решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3.
Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!
Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля. А х – 2 при х = 2 равно нулю! Так что всё честно.
И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!
Спокойно! Без паники!
В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ. Область Допустимых Значений.
Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых – дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
.
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель –
.
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
.
.
Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель – выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению
.
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 – корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y :
.
Корни этого уравнения:
или .
Из уравнения находим, что
.
Из уравнения находим, что
.
Итак, данное уравнение имеет четыре корня:
, .
[spoiler title=”источники:”]
http://megalektsii.ru/s62947t7.html
http://function-x.ru/sq_fractional_equations.html
[/spoiler]
Решение квадратных уравнений – самая любимая часть школьной математики. Почему самая любимая? Да потому что максимально стандартизирована. Смело могу утверждать, что 99 процентов людей помнит, что дискриминант применяется при решении квадратных уравнений, процентов 50 помнит его формулу…. А сколько людей знает, как эта формула выводится? Я думаю, немного. Исправим это недоразумение прямо сейчас.
Пусть дано квадратное уравнение вида
Проведем некоторые преобразования:
Естественно, что поделили на а не равное 0. Произведем нехитрые преобразования, чтобы выделить полный квадрат в левой части уравнения:
Слева в нашем уравнении полный квадрат, справа же сведем две дроби в одну. Отметим, что слева полный квадрат, всегда больший или равный нулю. Числитель дроби справа – это дискриминант, от знака которого зависят решения квадратного уравнения.
Небольшая ремарка: строго говоря, фраза “дискриминант квадратного уравнения” не совсем корректна. Математики вводят вполне конкретное понятие “дискриминанта многочлена” ( в нашем случае – это дискриминант квадратного трехчлена)
Рассмотрим три случая. В первом говорят, что квадратное уравнение не имеет корней, но многие знают, что необходимо уточнять «не имеет вещественных корней», так как в этом случае корни будут комплексными числами.
Во втором случае уравнение имеет единственный корень, но правильнее будет сказать два совпадающих корня.
В третьем случае уравнение имеет два различных вещественных корня
Теперь Вы знаете, откуда «вылезает» дискриминант квадратного уравнения. Кстати, помните теорему Виета? С ней квадратные уравнения решать временами проще и быстрее.
Кстати, есть конкретные формулы определения дискриминанта кубического уравнения и уравнения четвертой степени.
Достаточно сложно для запоминания, не так ли?
************************************************************************
Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием.
**************************************************************************
О чем я еще пишу:
Теорема неслучайности: неравенство Чебышева
Про факториал
Как запомнить синус и косинус основных углов?
Правда интересные числа, “мамой клянусь”
Экзотические тригонометрические формулы, которые не дают в школе
Квадратные уравнения с дробями и корень дискриминанта
Ученик
(18),
закрыт
5 месяцев назад
Федя Булкин
Оракул
(62728)
6 месяцев назад
Решай уравнение как будто коэффициенты – целые числа. Скажу больше – все прекрасно получается. Ничего делить не надо…ты формулу дискриминанта не знаешь? Делить будешь в формуле х, ну, ничего страшного, х запишешь в виде смешанного числа…зачем тебе периоды и бесконечные дроби?
Александр Уш. Ученик (18)
6 месяцев назад
?
Как мне решать уравнение и представлять, что дробь – это целое число? Дело в том, что если дискриминант больше нуля, то в формуле решения нужн знать его корень, который может быть как раз-таки бесконечным либо слишком большим
suffixПросветленный (21503)
6 месяцев назад
Какой нафиг дискриминант конкретно в этом уравнении ?
Федя – посмотрите мой выложенный ответ и может быть поймёте что советы надо давать не от балды !
Natali Belska
Просветленный
(36096)
6 месяцев назад
(3/11)*x^2 – 2x + 3 2/3 = 0
привести к общему знаменателю => избавишься от дроби:
(3x^2)/11 – 2x + 11/3 = 0
общий знаменатель 11*3 = 33 =>
(3/3) * (3x^2)/11 – (33/33) * 2x + (11/11) * 11/3 = 0
9x^2/33 – 66x/33 + 121/33 = 0
(9x^2 – 66x + 121) / 33 = 0
9x^2 – 66x + 121 = 0
(3x)^2 – 2*(3x)*11 + 11^2 = 0
(3x – 11)^2 = 0
3x = 11
x = 11/3
Для теоремы Виета надо привести к виду x^2 + bx + c = 0
9x^2 – 66x + 121 = 0 (то есть разделить всё на 9:
x^2 – (66/9)*x + 121/9 = 0
Дробным уравнением называется уравнение, в котором хотя бы одно из
слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением
является уравнение  .
.
Пример 1. Решить дробное уравнение:
 .
.
Решение. Воспользуемся основным свойством дроби с представим левую и
правую части этого уравнения в виде дробей с одинаковым знаменателем:
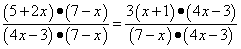 .
.
Эти дроби равны при тех и только тех значениях, при которых равны их
числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а
следовательно, и уравнение не имеет смысла.
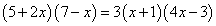 .
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
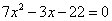 .
.
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются
корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
 .
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное
уравнение. Общий знаменатель —
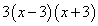 .
.
Заменим исходное уравнение целым. Для этого умножим обе его части на
общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к
квадратному уравнению
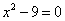 .
.
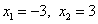 .
.
то же самое, если x = 3.
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а,
поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
 .
.
Решение. Найдём общий знаменатель дробей, входящих в данное
уравнение. Для этого знаменатели дробей разложим на множители:
 .
.
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
 .
.
 .
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно,
числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
 .
.
Решение. Введём новую переменную, обозначив 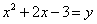
.
Получим уравнение с переменной y:
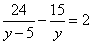 .
.
 или
или 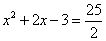 .
.
 .
.
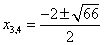 .
.
 ,
, 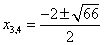 .
.
Проще говоря, это уравнения, в которых есть хотя бы одна дробь с переменной в знаменателе.
(frac{9x^2-1}{3x})(=0)
(frac{1}{2x}+frac{x}{x+1}=frac{1}{2})
(frac{6}{x+1}=frac{x^2-5x}{x+1})
Главное, что надо запомнить про дробно-рациональные уравнения – в них надо писать ОДЗ. И после нахождения корней – обязательно проверять их на допустимость. Иначе могут появиться посторонние корни, и все решение будет считаться неверным.
Алгоритм не заучивайте, 3-5 решенных уравнений – и он запомнится сам.
Пример. Решите дробно-рациональное уравнение (frac{x}{x-2} — frac{7}{x+2}=frac{8}{x^2-4})
Ответ: (3).
Пример. Найдите корни дробно-рационального уравнения (frac{x}{x+2} + frac{x+1}{x+5}-frac{7-x}{x^2+7x+10})(=0)
Ответ: (frac{1}{2}).
Как решать уравнения с дробями онлайн калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. В 5 классе школьники по математике изучают довольно много новых тем, одной из которых будет
дробные уравнения. Для многих это довольно сложная тема, в которой родители должны помочь разобраться своим
детям, а если родители забыли математику, то они всегда могут воспользоваться онлайн программами, решающими
уравнения. Так на примере вы сможете быстро понять алгоритм решения уравнений с дробями и помочь своему
ребенку.

Так же читайте нашу статью «Решить дробное уравнение онлайн
решателем»
Ниже для наглядности мы решим несложное дробное линейное уравнение следующего вида:
[frac{x-2}{3} — frac{3x}{2}=5]
Чтобы решить данного рода уравнения необходимо определить НОЗ и умножить на него левую и правую часть
уравнения:
НОЗ = 6
[frac {x-2}{3} — frac{3x}{2}=5]
Благодаря этому мы получим простое линейное уравнение, поскольку общий знаменатель, а также знаменатель
каждого дробного члена сократится:
[2(2-x)-9x=30]
Далее нам необходимо открыть скобки:
[2x-4-9x=30]
Сделаем перенос членов с неизвестной в левую сторону:
[-7x=30+4]
Выполним деление левой и правой части на -7:
[x=-frac{34}{7}]
Из полученного результата можно выделить целую часть, что и будет конечным результатом решения данного
дробного уравнения:
[x=-4frac {6}{7}]
Где можно решить уравнение с дробями онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Дробно-рациональные уравнения | Алгебра
Дробн0-рациональные уравнения (дробные рациональные уравнения или просто дробные уравнения) — это уравнения c одной переменной вида
где f(x) и g(x) — рациональные выражения, хотя бы одно из которых содержит алгебраическую дробь (то есть в таких уравнениях в знаменателе есть переменная).
В общем виде дробно-рациональные уравнения решают по следующей схеме:
1) Все слагаемые переносим в одну сторону.
2) Дроби приводим к НОЗ (наименьшему общему знаменателю).
3) После упрощения решаем уравнение типа «дробь равна нулю«.
В частных случаях дробно-рациональные уравнения могут быть решены с помощью замены переменной либо разложением на множители.
Начнем с рассмотрения примеров общего случая.
Решить дробно-рациональные уравнения:
Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:
Пришли к уравнению типа «дробь равна нулю» Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
Находим значения переменной, при которых знаменатель обращается в нуль, и исключаем их из области допустимых значений:
Теперь находим значения переменных, при которых числитель обращается в нуль:
Это — квадратное уравнение. Его корни
Оба корня удовлетворяют условиям x≠2, x≠ -4.Ответ: 5; -6.
Переносим все слагаемые в одну сторону и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной знаменатель обращается в нуль, поэтому их исключаем из ОДЗ.
Из двух корней квадратного уравнения
— второй не входит в ОДЗ. Поэтому в ответ включаем лишь первый корень.
Ответ: -4.
Переносим все слагаемые в одну сторону и приводим дроби к НОЗ:
Значение переменной, при котором знаменатель обращается в нуль, исключаем из ОДЗ:
Уравнение
— частный случай линейного уравнения. Оно имеет бесконечное множество решений: какое бы число мы не подставили вместо x, получим верное числовое равенство. Единственное значение x, который не входит в множество решений данного уравнения — 3.
Ответ: x — любое число, кроме 3.
Переносим все слагаемые в левую часть и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной дробь не имеет смысла, поскольку знаменатель обращается в нуль.
Так как 2 не входит в ОДЗ, данное уравнение не имеет корней.
Ответ: корней нет.
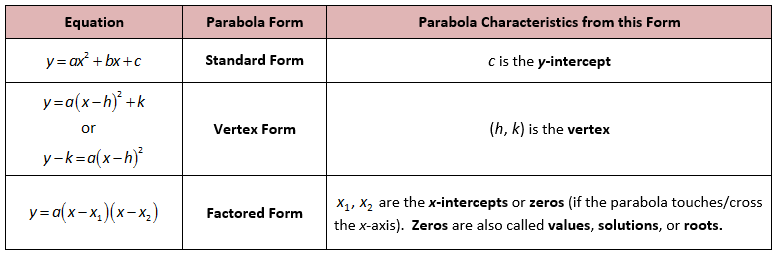
квадратичных уравнений
Пример квадратного уравнения :
Квадратные уравнения создают хорошие кривые, как этот:
Имя
Название Quadratic происходит от квадрата, означающего квадрат, потому что переменная получает квадрат (например, x 2 ).
Это также называется «уравнение степени 2» (из-за «2» на x )
Стандартная форма
Стандартная форма квадратного уравнения выглядит следующим образом:
- a , b и c являются известными значениями. a не может быть 0.
- « x » — это переменная , или неизвестно (мы пока не знаем).
Вот несколько примеров:
| 2x 2 + 5x + 3 = 0 | В этом a = 2 , b = 5 и c = 3 | |
| x 2 — 3x = 0 | Это немного сложнее:
|
|
| 5x — 3 = 0 | Ой! Это , а не квадратное уравнение: оно отсутствует x 2 (другими словами a = 0 , что означает, что оно не может быть квадратичным) |
поиграй с ним
Поиграйте в «Исследователь квадратичных уравнений», чтобы увидеть:
- график, который он делает, и
- решений (называемых «корнями»).
Скрытые квадратные уравнения!
Как мы видели ранее, стандартная форма квадратного уравнения равна
Но иногда квадратное уравнение выглядит не так!
Например:
| замаскированный | В стандартной форме | а, б и в | |
|---|---|---|---|
| x 2 = 3x — 1 | Переместить все термины в левую часть | x 2 — 3x + 1 = 0 | a = 1, b = −3, c = 1 |
| 2 (Вт 2 — 2 Вт) = 5 | Расширить (отменить скобки), и переместить 5 влево |
2 Вт 2 — 4 Вт — 5 = 0 | a = 2, b = −4, c = −5 |
| z (z − 1) = 3 | Разверните и переместите 3 влево | z 2 — z — 3 = 0 | a = 1, b = −1, c = −3 |
Как их решить?
«Решения » для квадратного уравнения — это где равно нулю .
Их также называют « корни », или иногда « нули »
Обычно есть 2 решения (как показано на этом графике).
И есть несколько способов найти решение:
Или мы можем использовать специальную квадратичную формулу :
Просто подключите значения a, b и c и выполните расчеты.
Мы рассмотрим этот метод более подробно сейчас.
О квадратичной формуле
Плюс / Минус
Прежде всего, что это за плюс / минус, что выглядит как ±?
± означает, что есть ДВА ответа:
x = −b + √ (b 2 — 4ac) 2a
x = −b — √ (b 2 — 4ac) 2a
Вот пример с двумя ответами:
Но так не всегда получается!
- Представьте, что кривая «просто касается» оси X.
- Или представьте, что кривая настолько высока, что и даже не пересекают ось X!
Здесь «Дискриминант» помогает нам …
Дискриминант
Видите ли вы b 2 — 4ac в формуле выше? Он называется Дискриминант , потому что он может «различать» между возможными типами ответа:
- , когда b 2 — 4ac положительно, мы получаем два реальных решения
- , когда он равен нулю, мы получаем ОДНО реальное решение (оба ответа одинаковы)
- , когда оно отрицательное, мы получаем пару комплексных решений
Комплексные решения? Давайте поговорим о них после того, как посмотрим, как использовать формулу.
Использование квадратичной формулы
Просто поместите значения a, b и c в квадратную формулу и выполните вычисления.
Пример: Решить 5x 2 + 6x + 1 = 0
Коэффициенты: а = 5, б = 6, с = 1
Квадратичная формула: x =
−b ± √ (b 2 — 4ac)
2а
Положите в a, b и c: x =
−6 ± √ (6 2 — 4 × 5 × 1)
2 × 5
Решить: х =
−6 ± √ (36 — 20)
10
х =
−6 ± √ (16)
10
х =
−6 ± 4
10
x = −0.2 или −1
Ответ: x = −0.2 или x = −1
И мы видим их на этом графике.
| Чек -0,2 : | 5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1 = 5 × (0,04) + 6 × (–0,2) + 1 = 0,2 — 1,2 + 1 = 0 |
|
| Чек -1 : | 5 × ( -1 ) 2 + 6 × ( -1 ) + 1 = 5 × (1) + 6 × (-1) + 1 = 5 — 6 + 1 = 0 |
Вспоминая Формулу
Добрая читательница предложила спеть ее для «Pop Goes the Weasel»:
| ♫ | «x равно минус b | ♫ | «Все вокруг куста шелковицы | |
| плюс или минус квадратный корень | Обезьяна преследовала ласку | |||
| б-квадрат минус четыре а с | Обезьяна подумала, что все в порядке | |||
| ВСЕ более двух « | Поп! идет ласка « |
Попробуйте спеть его несколько раз, и он застрянет у вас в голове!
Или вы можете вспомнить эту историю:
х =
−b ± √ (b 2 — 4ac)
2а
«Отрицательный мальчик думал о да или нет о том, чтобы пойти на вечеринку,
на вечеринке он говорил с квадратным парнем, но не с 4 потрясающими цыпочками.
Все закончилось в 2 часа ночи. «
Комплексные решения?
Когда дискриминант (значение b 2 — 4ac ) отрицателен, мы получаем пару комплексных решений … что это значит?
Это означает, что наш ответ будет включать в себя мнимые числа. Вот Это Да!
Пример: Решить 5x 2 + 2x + 1 = 0
Коэффициенты : : a = 5, b = 2, c = 1
Обратите внимание, что дискриминант является отрицательным: b 2 — 4ac = 2 2 — 4 × 5 × 1
= −16
Используйте квадратичную формулу : x =
-2 ± √ (−16)
10
√ (−16)
= 4 i
(где i — мнимое число √ − 1)
Итак: х =
-2 ± 4 i
10
Ответ: x = −0.2 ± 0,4 i
График не пересекает ось X. Вот почему мы получили комплексные числа.
В некотором смысле это проще: нам не нужно больше вычислений, просто оставьте это как -0,2 ± 0,4 i .
Пример: Решить x 2 — 4x + 6,25 = 0
Коэффициенты : : a = 1, b = −4, c = 6.25
Обратите внимание, что дискриминант отрицателен: b 2 — 4ac = (−4) 2 — 4 × 1 × 6.25
= −9
Используйте квадратичную формулу : x = — (- 4) ± √ (−9) 2
√ (−9) = 3 i
(где i — мнимое число √ − 1)
Итак: x = 4 ± 3 i 2
Ответ: x = 2 ± 1,5 i
График не пересекает ось X.Вот почему мы получили комплексные числа.
, НО перевернутое зеркальное изображение нашего уравнения пересекает ось X при 2 ± 1,5 (примечание: отсутствует i ).
Просто интересный факт для вас!
Резюме
- Квадратичное уравнение в стандартной форме: топор 2 + bx + c = 0
- Квадратичные уравнения могут быть учтены
- Квадратичная формула: x =
−b ± √ (b 2 — 4ac)
2а - Когда дискриминант ( b 2 −4ac ) равен:
- положительных, есть 2 реальных решения
- ноль, есть одно реальное решение
- минус, есть 2 комплексных решения
,
Алгебра. Квадратичные уравнения. Часть II
Пол Заметки Онлайн
Ноты
Быстрая навигация
Скачать
- Перейти к
- Ноты
- Проблемы практики
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Квадратичные уравнения — Часть I
- Квадратичные уравнения: краткое изложение
- глав
- Предварительные сведения
- Графика и функции
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
Уравнения
- Предварительные
.
Решение квадратичных уравнений
Решение квадратичных уравнений
Квадратное уравнение — это уравнение, которое можно записать как
топор 2 + bx + c = 0
когда а 0.
Существует три основных метода решения квадратных уравнений: факторинг, использование квадратной формулы и заполнение квадрата.
Факторинг
Чтобы решить квадратное уравнение с помощью факторинга,
-
Поместите все члены на одну сторону знака равенства, оставив ноль на другой стороне.
-
Фактор.
-
Установите каждый фактор равным нулю.
-
Решите каждое из этих уравнений.
-
Проверьте, вставив свой ответ в исходное уравнение.
Пример 1
Решить x 2 — 6 x = 16.
Следуя инструкциям,
x 2 — 6 x = 16 становится x 2 — 6 x — 16 = 0
Фактор.
( x — 8) ( x + 2) = 0
Установка каждого фактора на ноль, 
Тогда, чтобы проверить, 
Оба значения, 8 и –2, являются решениями исходного уравнения.
Пример 2
Решить y 2 = — 6 y — 5.
Установка всех слагаемых, равных нулю,
y 2 + 6 y + 5 = 0
Фактор.
( y + 5) ( y + 1) = 0
Установка каждого коэффициента на 0, 
Для проверки, y 2 = –6 y — 5

Квадратик с отсутствующим термином называется неполным квадратичным (до тех пор, пока не исчезнет топор 2 ).
Пример 3
Решить x 2 — 16 = 0.
Фактор.

Для проверки, x 2 — 16 = 0

Пример 4
Решить x 2 + 6 x = 0.
Фактор.

Для проверки, x 2 + 6 x = 0

Пример 5
Решить 2 x 2 + 2 x — 1 = x 2 + 6 x — 5.
Во-первых, упростите, поместив все термины на одну сторону и объединив одинаковые термины.

Теперь фактор.

Для проверки: 2 x 2 + 2 x — 1 = x 2 + 6 x — 5

Квадратичная формула
Многие квадратные уравнения не могут быть решены с помощью факторинга. Это обычно верно, когда корни или ответы не являются рациональными числами.Второй метод решения квадратных уравнений предполагает использование следующей формулы: 
a, b, и c взяты из квадратного уравнения, записанного в его общей форме
топор 2 + bx + c = 0
, где a — это число перед x 2 , b — это число перед x , а c — это число без переменной рядом с ним (a ,к.а., «константа»).
При использовании квадратной формулы вы должны знать о трех возможностях. Эти три возможности отличаются частью формулы, называемой дискриминантом. Дискриминант — это значение под знаком радикала, b 2 — 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее значение:
-
Два разных реальных корня, если дискриминант b 2 — 4 ac является положительным числом.
-
Один действительный корень, если дискриминант b 2 — 4 ac равен 0.
-
Нет реального корня, если дискриминант b 2 — 4 ac является отрицательным числом.
Пример 6
Решить для x : x 2 — 5 x = –6.
Установка всех слагаемых, равных 0,
x 2 — 5 x + 6 = 0
Затем подставьте 1 (который понимается перед x 2 ), –5 и 6 для a , b и c, соответственно в квадратной формуле и упростите.

Поскольку дискриминант b 2 — 4 ac положителен, вы получаете два разных реальных корня.
Пример
производит рациональные корни. В примере
квадратная формула используется для решения уравнения, корни которого не рациональны.
Пример 7
Решить за у : у 2 = –2y + 2.
Установка всех слагаемых, равных 0,
y 2 + 2 y — 2 = 0
Затем замените 1, 2 и –2 для на , b и c, соответственно в квадратной формуле и упростите.

Обратите внимание, что два корня иррациональны.
Пример 8
Решить для x : x 2 + 2 x + 1 = 0.
Подставляя в квадратную формулу,

Поскольку дискриминант b 2 — 4 ac равен 0, уравнение имеет один корень.
Квадратичная формула также может быть использована для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в системе вещественных чисел.
Пример 9
Решить для x : x ( x + 2) + 2 = 0 или x 2 + 2 x + 2 = 0.
Подставляя в квадратную формулу,

Поскольку дискриминант b 2 — 4 ac отрицателен, это уравнение не имеет решения в системе вещественных чисел.
Но если бы вы выразили решение, используя мнимые числа, решения были бы  .
.
Завершение квадрат
Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.
-
Поместите уравнение в форму ax 2 + bx = — c .
-
Убедитесь, что a = 1 (если a ≠ 1, перед продолжением умножьте уравнение на
 ).
). -
Используя значение b из этого нового уравнения, добавьте
 к обеим сторонам уравнения, чтобы сформировать идеальный квадрат в левой части уравнения.
к обеим сторонам уравнения, чтобы сформировать идеальный квадрат в левой части уравнения. -
Найдите квадратный корень с обеих сторон уравнения.
-
Решите полученное уравнение.
Пример 10
Решить для x : x 2 — 6 x + 5 = 0.
Упорядочить в виде

Поскольку a = 1, добавьте  или 9 с обеих сторон, чтобы завершить квадрат.
или 9 с обеих сторон, чтобы завершить квадрат.

Возьмите квадратный корень с обеих сторон.
x — 3 = ± 2
Решить.

Пример 11
Решить за г. : г. 2 + 2 г. — 4 = 0.
Упорядочить в виде

Поскольку a = 1, добавьте  или 1 к обеим сторонам, чтобы завершить квадрат.
или 1 к обеим сторонам, чтобы завершить квадрат.

Возьмите квадратный корень с обеих сторон.

Решить.

Пример 12
Решить для x : 2 x 2 + 3 x + 2 = 0.
Упорядочить в виде

Поскольку a ≠ 1, умножьте уравнение на  .
.

Добавьте  или
или  в обе стороны.
в обе стороны.

Возьмите квадратный корень с обеих сторон.

Нет решения в реальной системе счисления. Возможно, вам будет интересно узнать, что завершающий квадратный процесс для решения квадратных уравнений был использован для уравнения ax 2 + bx + c = 0 для получения квадратной формулы.
,
Quadratic Equation
Привет друзья! Квадратичные уравнения являются неотъемлемой частью математики, которая также применяется в различных других областях. Поэтому мы создали этот сайт, чтобы объяснить вам , что такое квадратное уравнение. После понимания концепции квадратичных уравнений вы сможете легко решать квадратные уравнения .
Теперь давайте объясним вам, что такое квадратное уравнение. Это математическое уравнение с наибольшей степенью 2.Он имеет форму топор ² + bx + c . Здесь x представляет неизвестное значение, а a, b и c представляют известные числа. Решения квадратных уравнений можно использовать с помощью квадратной формулы. Существуют и другие методы поиска решений квадратных уравнений, такие как разложение на множители, заполнение квадрата или построение графиков. Поскольку квадратные уравнения имеют наивысшую степень 2, всегда будет два решения для x, которые будут приняты. Эти значения x, которые удовлетворяют уравнению, называются корнями или нулями уравнения.Следовательно, квадратное уравнение всегда будет иметь два корня или решения.
Здесь, в этой статье, мы попытались объяснить вам все понятия квадратичных уравнений. Если вы студент, то изучение этих понятий очень важно, поскольку это поможет вам решить проблемы в школе. Это важная концепция, которая имеет широкий спектр применения в таких областях, как физика, химия, машиностроение и т. Д.
Определение уравнения с квадратичной формулой
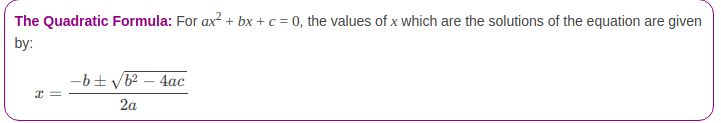
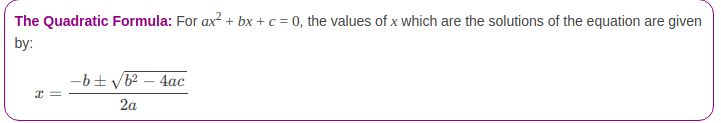
Мы обсудили с вами общий формат квадратного уравнения.Теперь, если вам требуется решить квадратное уравнение, вы должны использовать квадратную формулу. Любое квадратное уравнение имеет два решения или корни. Таким образом, вы получите два корня, один в «+» и один в «-», и оба являются решениями уравнения.
Здесь мы предоставили вам таблицу с квадратной формулой, поэтому вам будет легко ее запомнить и применить.
Калькулятор квадратного уравнения
Калькулятор квадратного уравнения — это специальный калькулятор, который используется для решения сложных квадратных уравнений.Хотя для вычисления корней квадратного уравнения можно использовать научный калькулятор, он не всегда удобен. Поэтому многие онлайн-сайты предоставляют калькулятор квадратного уравнения, который очень прост в использовании. Вам просто нужно ввести известные значения a, b и c. Он рассчитает корни квадратного уравнения автоматически.
Здесь мы предоставили вам калькулятор квадратного уравнения, где вам просто нужно ввести коэффициенты квадратного уравнения.
Рабочие таблицы по квадратным уравнениям PDF


Даже если вы знаете, как правильно решать квадратные уравнения, вам нужно попрактиковаться в их решении, чтобы овладеть концепцией. Как студенты, практика темы важна для того, чтобы быть прекрасной в этом. Следовательно, вы можете оценить, как много вы узнали о квадратных уравнениях, решив задачи, приведенные в этой таблице.
Этот лист представлен в формате PDF, поэтому вы можете взять его распечатку и взять с собой куда угодно.
График квадратного уравнения
График квадратного уравнения представляет собой график, отображающий значения всех корней квадратного уравнения. Поскольку в квадратном уравнении существуют как отрицательные, так и положительные корни, график принимает форму параболы. Следовательно, вы можете построить график квадратного уравнения, найдя различные корни x, которые решают равенство.
Чтобы помочь вам лучше понять график квадратичного уравнения, мы предоставили вам график квадратного уравнения, который поможет вам понять, как вы можете построить график квадратичного уравнения.
Стандартная форма квадратного уравнения
Стандартная форма квадратного уравнения — это уравнение в форме ах 2 + bx + c = 0. Здесь x — неизвестное значение, и a, b и c являются переменными. Но иногда квадратные уравнения могут не прийти в стандартной форме, и нам, возможно, придется расширить их.
Здесь мы предоставили вам таблицу, показывающую примеры различных форм квадратных уравнений, таких как форма вершины и фактор-форма.
Вершинная форма квадратного уравнения задается следующим образом:
f ( x ) = a ( x — h ) 2 + k , где ( ч, k ) это вершина параболы.
Факторизованная форма квадратного уравнения говорит нам о корнях квадратного уравнения. Он записывается в виде a⋅ (x − p) ⋅ (x − q) или a⋅ (x − p) 2
Дискриминант квадратного уравнения
В математике дискриминант является полиномиальной функцией своего коэффициента , что позволяет нам иметь представление о некоторых свойствах корней без их вычисления.Следовательно, в случае квадратного уравнения дискриминант является частью квадратного уравнения под квадратным корнем. Это помогает нам определить число корней для квадратного уравнения.
Здесь мы предоставили вам пример дискриминанта квадратного уравнения.
Как решить квадратное уравнение
Как известно, квадратное уравнение является полиномом со степенью 2. Существуют различные методы, с помощью которых можно решить квадратное уравнение.Ниже приведены методы решения квадратного уравнения:
- Факторинг
Давайте посмотрим, как использовать метод факторинга для решения квадратного уравнения.
Например, давайте решим уравнение (x + 4) (x-3) = 0
. Мы будем сохранять значение каждого фактора равным 0.
(x + 4) = 0 и (x-3) = 0
Следовательно, x + 4 — 4 = 0 -4; или x-3 + 3 = 0 + 3
x = -4 или x = 3
2. Завершение квадрата
Иногда некоторые квадратные уравнения могут быть учтены как идеальные квадраты.
Например, квадратное уравнение x² + 6x + 5 не является идеальным квадратом. Но если мы добавим 4 к нему, он станет идеальным квадратом. И результирующее выражение, которое мы получили бы (x + 3) ².
3. Квадратичная формула
Это наиболее распространенный метод решения квадратного уравнения. Это включает использование квадратной формулы, чтобы найти решение или корни квадратного уравнения.
Ниже приведена квадратная формула, используемая для решения любого квадратного уравнения:
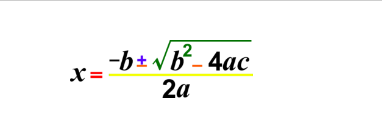
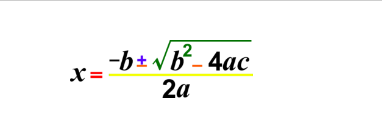
4.Graphing
Используя этот метод, все корни квадратного уравнения можно получить, подставив любое значение для x, которое решает равенство.
Прежде чем графически решить квадратное уравнение, мы должны понять, что такое x-intercept и y-intercept. X-перехват относится к корням квадратичных уравнений, которые пересекают график по оси X. Точно так же Y-перехват относится к корням квадратного уравнения, которое пересекает график по оси Y. Значимость x и y-перехватчиков заключается в том, что они изображают насест или решение квадратного уравнения.Вы можете использовать любое значение для x-перехвата, чтобы найти различные значения y-перехвата и построить соответствующие точки на графике.
Использование квадратичной формулы
Мы рассказали вам о различных методах, с помощью которых вы можете найти решения квадратных уравнений. В то время как другие обычно используемые методы, такие как факторинг и построение графиков, могут использоваться для поиска решений для квадратных уравнений, процесс может усложниться, и результат также может быть неточным.
Следовательно, наиболее предпочтительным методом решения квадратного уравнения является использование квадратной формулы.
Квадратичная формула дается в виде:
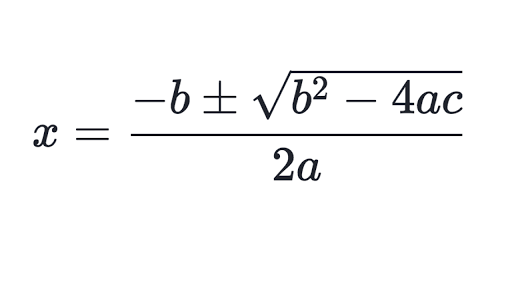
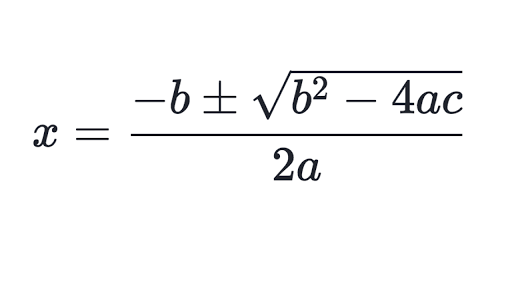
Здесь мы объясним вам, как вы можете применять квадратное уравнение для решения задач. Вы можете следовать этим пошаговым инструкциям для решения любого квадратного уравнения:
Например, возьмите квадратное уравнение x 2 + 2x + 1 = 0
Теперь давайте найдем дискриминанты уравнения:
Дискриминант формула = b 2 — 4ac
Применение значений a, b и c в приведенном выше уравнении:
22 — 4 × 1 × 1 = 0
Теперь примените квадратную формулу:
x = (−2 ± √0) / 2 = −2/2
Следовательно, x = -1
Решатель квадратичных уравнений
Часто мы сталкиваемся с решением сложных квадратных уравнений, которое может быть сложным и требует сложных вычислений.Кроме того, существует риск ошибочного результата. Таким образом, вы можете воспользоваться помощью решателя квадратного уравнения, который в основном калькулятор квадратного уравнения.
Этот калькулятор прост в использовании и даст вам правильные результаты в считанные секунды. Вам просто нужно ввести коэффициенты для a, b и c, и он автоматически найдет для вас значение обоих корней квадратного уравнения.
Чтобы объяснить вам, как вы можете решать квадратные уравнения онлайн с помощью решателя квадратичных уравнений, здесь мы предоставили вам видео.
Заключение
Таким образом, в этой статье мы попытались объяснить вам все понятия квадратичных уравнений и различные методы, с помощью которых вы можете их решать. Используя такие методы, как факторинг и построение графиков, вы можете легко найти решения любого квадратного уравнения. Но наиболее предпочтительным методом, который можно использовать для решения любого квадратного уравнения, является квадратная формула. Мы надеемся, что эта статья помогла вам лучше понять квадратные уравнения и позволит вам легко решить любое квадратное уравнение.
.