Найти корни квадратного уравнения
Вычислить корни квадратного уравнения,
коэффициенты a, b, c которого вводятся с клавиатуры.
Решение задачи на языке программирования Python
Квадратное уравнение имеет вид
ax2 + bx + c = 0
При его решении сначала вычисляют дискриминант по формуле
D = b2 - 4ac
Если D > 0, то квадратное уравнение имеет два корня:
,
Если D = 0, то 1 корень:
И если D < 0, то делают вывод, что корней нет.
Таким образом, программа для нахождения корней квадратного уравнения должна иметь три ветви условного оператора.
Функция float преобразует переданный ей аргумент в вещественное число.
import math print("Введите коэффициенты для уравнения") print("ax^2 + bx + c = 0:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) discr = b ** 2 - 4 * a * c print("Дискриминант D = %.2f" % discr) if discr > 0: x1 = (-b + math.sqrt(discr)) / (2 * a) x2 = (-b - math.sqrt(discr)) / (2 * a) print("x1 = %.2f nx2 = %.2f" % (x1, x2)) elif discr == 0: x = -b / (2 * a) print("x = %.2f" % x) else: print("Корней нет")
Примеры выполнения кода:
Введите коэффициенты для уравнения ax^2 + bx + c = 0: a = 2 b = 4 c = 2 Дискриминант D = 0.00 x = -1.00
Введите коэффициенты для уравнения ax^2 + bx + c = 0: a = 3.2 b = -7.8 c = 1 Дискриминант D = 48.04 x1 = 2.30 x2 = 0.14
Введите коэффициенты для уравнения ax^2 + bx + c = 0: a = 8 b = 4 c = 2 Дискриминант D = -48.00 Корней нет
Обратите внимание, что для данной программы коэффициент a не должен быть равен нулю. Иначе в теле условного оператора будет происходить попытка деления на 0, что приведет к аварийному завершению программы.
Если a = 0, то квадратное уравнение превращается в линейное, которое решается иным способом. Оно всегда имеет один корень.
Больше задач в PDF
Здравствуйте, дорогие друзья. Сегодня мы напишем простенький алгоритм на языке программирования Python. Естественно, существует огромное количество сайтов для подсчёта дискриминанта. Но я предлагаю вам блеснуть знаниями перед товарищами и вашими учителями информатики и математики и написать исходный код, считающий дискриминант.
Внимательно смотрим на скриншот и читаем комментарии.
Далее сохраняем наш исходный код и запускаем написанную программу по нажатию клавиши F5.
Вот такая вот не сложная, но достаточно полезная программа по решению квадратного уравнения и нахождению корней дискриминанта на Python, версия языка 3.8.2.
Если информация была интересной для вас, то заходите на наш Ютуб-канал ПиМ [ZveKa]. Там много всего интересного. До новых встреч на просторах Яндекс Дзена.
Квадратное уравнение в Python:
Квадратное уравнение образовано от латинского термина «quadrates», что означает «квадрат». Это специальный тип уравнения, имеющий форму:
ах2+bх+с=0
Здесь «x» неизвестное, которое вы должны найти, «a», «b», «c» задает числа, такие что «a» не равно 0. Если a = 0, то уравнение становится линейным, а не квадратным. В уравнении a, b и c называются коэффициентами.
Возьмем пример решения квадратного уравнения 8x2 + 16x + 8 = 0.
См. этот пример:
# import complex math module
import cmath
a = float(input('Enter a: '))
b = float(input('Enter b: '))
c = float(input('Enter c: '))
# calculate the discriminant
d =(b**2) -(4*a*c)
# find two solutions
sol1 =(-b-cmath.sqrt(d))/(2*a)
sol2 =(-b+cmath.sqrt(d))/(2*a)
print('The solution are {0} and {1}'.format(sol1,sol2))
Выход:
Enter a: 8 Enter b: 5 Enter c: 9 The solution are(-0.3125-1.0135796712641785j) and(-0.3125+1.0135796712641785j)
Объяснение:
В первой строке мы импортировали модуль cmath и определили три переменные с именами a, b и c, которые получают ввод от пользователя. Затем вычисляем дискриминант по формуле. С помощью метода cmath.sqrt() мы вычислили два решения и распечатали результат.
Второй метод
Мы можем получить решение квадратного уравнения, используя прямую формулу. Давайте разберем следующий пример.
Вышеприведенная формула состоит из следующих случаев.
- Если b2 < 4ac, то корни комплексные (не вещественные). Например – x2 + x + 1, корни -0,5 + i1,73205 и +0,5 – i1,73205.
- Если b2 == 4ac, то оба корня одинаковы. Например – x2 + x + 1, корни равны -0,5 + i1,73205 и +0,5 – i1,73205.
- Если b2 > 4ac, то корни действительны и различны. Например – х2 – 7 х – 12, корни 3 и 4.
Пример:
# Python program to find roots of quadratic equation
import math
# function for finding roots
def findRoots(a, b, c):
dis_form = b * b - 4 * a * c
sqrt_val = math.sqrt(abs(dis_form))
if dis_form > 0:
print(" real and different roots ")
print((-b + sqrt_val) /(2 * a))
print((-b - sqrt_val) /(2 * a))
elif dis_form == 0:
print(" real and same roots")
print(-b /(2 * a))
else:
print("Complex Roots")
print(- b /(2 * a), " + i", sqrt_val)
print(- b /(2 * a), " - i", sqrt_val)
a = int(input('Enter a:'))
b = int(input('Enter b:'))
c = int(input('Enter c:'))
# If a is 0, then incorrect equation
if a == 0:
print("Input correct quadratic equation")
else:
findRoots(a, b, c)
Выход:
Enter a:7 Enter b:5 Enter c:2 Complex Roots -0.35714285714285715 + i 5.5677643628300215 -0.35714285714285715 - i 5.5677643628300215
Объяснение:
В приведенном выше коде мы импортировали математический модуль и определили формулу для вычисления дискриминанта. Затем мы определили функцию findRoots, которая принимает три целых значения в качестве аргументов. Затем мы проверили корни с помощью оператора if-elif-else.
Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Перейти к содержанию
На чтение 2 мин Просмотров 643 Опубликовано 28.02.2023
Содержание
- Введение
- Решение квадратных уравнений в Python
- Заключение
Введение
В ходе статьи научимся решать квадратные уравнения при помощи языка программирования Python.
Решение квадратных уравнений в Python
Для написания кода нам понадобится метод sqrt() из модуля math, который возвращает квадратный корень числа. Импортируем его:
Теперь дадим пользователю возможность ввести коэффициенты a, b и c:
from math import sqrt
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))Вычислим дискриминант по формуле:
from math import sqrt
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
d = b**2 - 4 * a * cПерейдём к нахождению корней. Зададим условие, что если дискриминант больше нуля, то x1 и x2 будут высчитаны по формуле:
x1, x2 = frac{-bpmsqrt{D}}{2a}
from math import sqrt
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
d = b**2 - 4 * a * c
if d > 0:
x1 = (-b + sqrt(d) / (2 * a))
x2 = (-b - sqrt(d) / (2 * a))
print(f'x1 = {x1:.2f}; x2 = {x2:.2f}')Если же дискриминант равен нулю, то будет всего один корень по формуле:
from math import sqrt
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
d = b**2 - 4 * a * c
if d > 0:
x1 = (-b + sqrt(d) / (2 * a))
x2 = (-b - sqrt(d) / (2 * a))
print(f'x1 = {x1:.2f}; x2 = {x2:.2f}')
elif d == 0:
x1 = -b / (2 * a)
print(f'x1 = {x1:.2f}')Если же дискриминант оказался отрицательным, это означает что корней нет:
from math import sqrt
a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))
d = b**2 - 4 * a * c
if d > 0:
x1 = (-b + sqrt(d) / (2 * a))
x2 = (-b - sqrt(d) / (2 * a))
print(f'x1 = {x1:.2f}; x2 = {x2:.2f}')
elif d == 0:
x1 = -b / (2 * a)
print(f'x1 = {x1:.2f}')
else:
print('Нет корней')Заключение
В ходе статьи мы с Вами написали небольшую программку на языке программирования Python, которая умеет решать квадратные уравнения. Надеюсь Вам понравилась статья, желаю удачи и успехов! 🙂
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a quadratic equation the task is solve the equation or find out the roots of the equation. Standard form of quadratic equation is –
ax2 + bx + c = 0 where, a, b, and c are coefficient and real numbers and also a ≠ 0. If a is equal to 0 that equation is not valid quadratic equation.
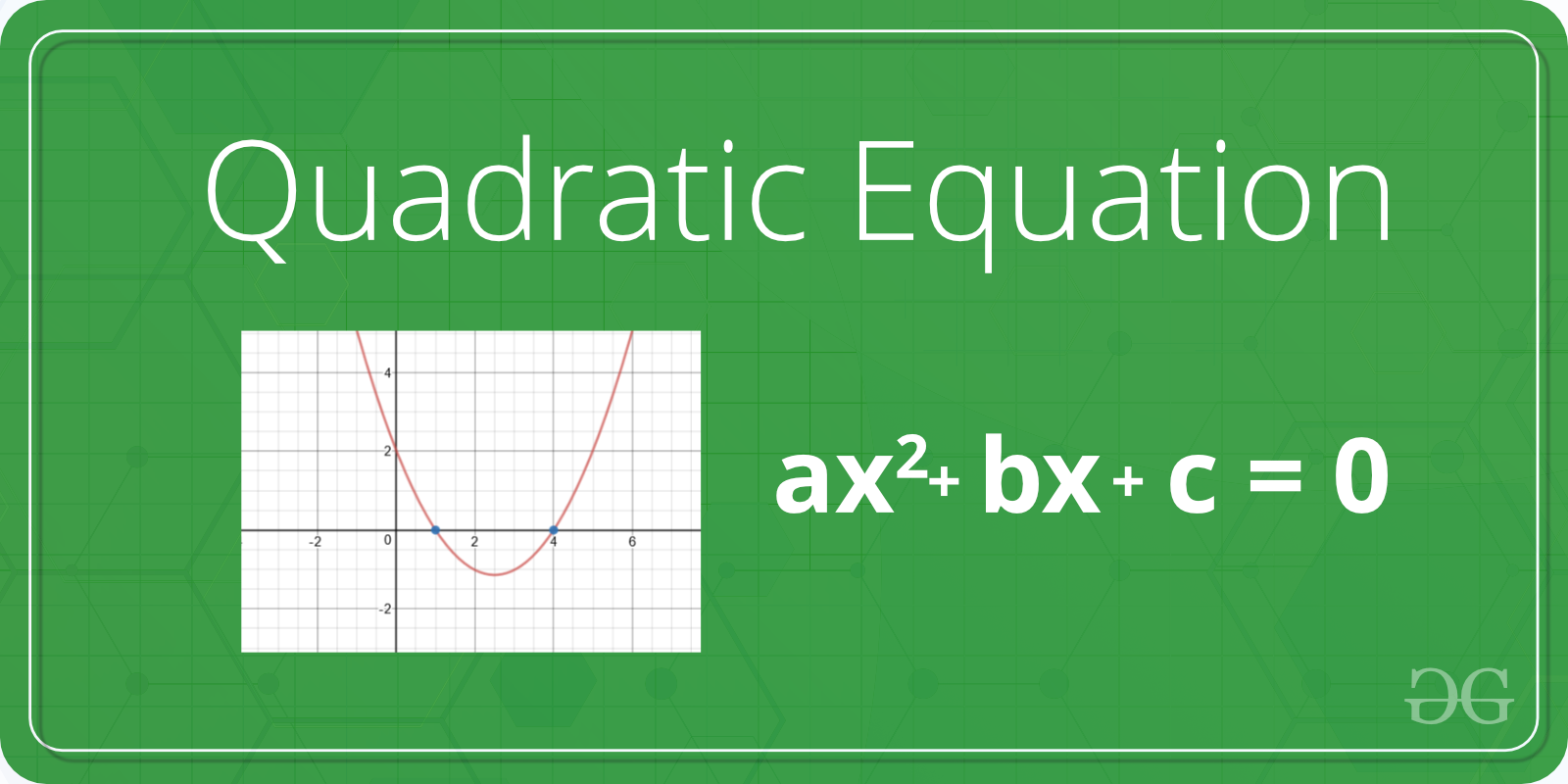Examples:
Input :a = 1, b = 2, c = 1 Output : Roots are real and same -1.0 Input :a = 2, b = 2, c = 1 Output : Roots are complex -0.5 + i 2.0 -0.5 - i 2.0 Input :a = 1, b = 10, c = -24 Output : Roots are real and different 2.0 -12.0
Method 1: Using the direct formula Using the below quadratic formula we can find the root of the quadratic equation. 
There are following important cases.
If b*b < 4*a*c, then roots are complex (not real). For example roots of x2 + x + 1, roots are -0.5 + i1.73205 and -0.5 - i1.73205 If b*b == 4*a*c, then roots are real and both roots are same. For example, roots of x2 - 2x + 1 are 1 and 1 If b*b > 4*a*c, then roots are real and different. For example, roots of x2 - 7x - 12 are 3 and 4
Python3
import math
def equationroots( a, b, c):
dis = b * b - 4 * a * c
sqrt_val = math.sqrt(abs(dis))
if dis > 0:
print(" real and different roots ")
print((-b + sqrt_val)/(2 * a))
print((-b - sqrt_val)/(2 * a))
elif dis == 0:
print(" real and same roots")
print(-b / (2 * a))
else:
print("Complex Roots")
print(- b / (2 * a), " + i", sqrt_val)
print(- b / (2 * a), " - i", sqrt_val)
a = 1
b = 10
c = -24
if a == 0:
print("Input correct quadratic equation")
else:
equationroots(a, b, c)
Output:
real and different roots 2.0 -12.0
Method 2: Using the complex math module First, we have to calculate the discriminant and then find two solution of quadratic equation using cmath module.
Python3
import cmath
a = 1
b = 4
c = 2
dis = (b**2) - (4 * a*c)
ans1 = (-b-cmath.sqrt(dis))/(2 * a)
ans2 = (-b + cmath.sqrt(dis))/(2 * a)
print('The roots are')
print(ans1)
print(ans2)
Output:
The roots are (-3.414213562373095+0j) (-0.5857864376269049+0j)
Last Updated :
16 Mar, 2023
Like Article
Save Article
