Это уравнение вида ax2+bx+c=0ax^2 + bx + c = 0,
где aa – коэффициент перед x2x^2,
bb – коэффициент перед xx,
cc – свободное число.
Существуют разные способы нахождения корней квадратного уравнения. Пожалуй, самый основной и распространенный способ – через вычисление дискриминанта. В этом случае он рассчитывается по формуле:
D=b2–4acD = b^2 – 4ac
Если второй коэффициент уравнения четный, можно решать уравнение через kk, тогда будет другая формула дискриминанта:
D1=k2–acD_1 = k^2 – ac
Если первый коэффициент уравнения равен 1, то можно воспользоваться теоремой Виета, которая имеет 2 условия:
x1+x2=−bx_1 + x_2 = -b
x1⋅x2=cx_1 cdot x_2 = c
Но если мы захотим решить уравнение основным способом, ошибки не будет. Нахождение корней уравнения через дискриминант – универсальный способ, а остальные введены для удобства вычислений.
Задача 1
Решим уравнение: 3×2+7x−6=0.3x^2 + 7x – 6 = 0.
Обозначим коэффициенты:
a=3a = 3,
b=7b = 7,
c=−6c = -6
Далее находим дискриминант по формуле:
D=b2–4acD = b^2 – 4ac
D=72–4∗3∗(−6)=49+72=121=112D = 7^2 – 4 * 3 * (-6) = 49 + 72 = 121 = {11}^2
D>0D > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b – √D) / 2a
Подставляем численные значения:
x1=(−7+11)/2∗3=4/6=23x_1 = (-7 + 11) / 2*3 = 4 / 6 = frac{2}{3}
x2=(−7–11)/2∗3=−18/6=−3x_2 = (-7 – 11) / 2*3 = -18 / 6 = -3
Ответ: x1=23x_1 = frac{2}{3}, x2=−3x_2 = -3.
Задача 2
Решим уравнение: −x2+7x+8=0.-x^2 + 7x + 8 = 0.
Обозначим коэффициенты:
a=−1a = -1,
b=7b = 7,
c=8.c = 8.
Далее находим дискриминант по формуле:
D=b2–4acD = b^2 – 4ac
D=72–4⋅(−1)⋅8=49+32=81=92D = 7^2 – 4 cdot (-1) cdot 8 = 49 + 32 = 81 = 9^2
D>0D > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b – √D) / 2a
Подставляем численные значения:
x1=(−7+9)/2∗(−1)=2/(−2)=−1x_1 = (-7 + 9) / 2 * (-1) = 2 / (-2) = -1
x2=(−7–9)/2∗(−1)=−16/(−2)=8x_2 = (-7 – 9) / 2 * (-1) = -16 / (-2) = 8
Ответ: x1=−1x_1 = -1, x2=8x_2 = 8.
Задача 3
Решим уравнение: 4×2+4x+1=0.4x^2 + 4x + 1 = 0.
Обозначим коэффициенты:
a=4a = 4,
b=4b = 4,
c=1.c = 1.
Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac
D=42–4⋅4⋅1=16–16=0D = 4^2 – 4 cdot 4 cdot 1 = 16 – 16 = 0
D=0D = 0 – значит, уравнение имеет 1 корень.
Находим корень уравнения по следующей формуле: x=−b/2ax = -b / 2a
Подставляем численные значения:
x=−4/2⋅4=−4/8=−1/2=−0,5x = -4 / 2 cdot 4 = -4 / 8 = -1 / 2 = -0,5
Ответ: x=−0,5.x = -0,5.
Задача 4
Решим уравнение: 2×2+x+1=0.2x^2 + x + 1 = 0.
Обозначим коэффициенты:
a=2a = 2,
b=1b = 1,
c=1.c = 1.
Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac
D=12–4∗2∗1=1–8=−7D = 1^2 – 4 * 2 * 1 = 1 – 8 = -7
D<0D < 0 – значит, уравнение корней не имеет.
Ответ: корней нет.
Решение квадратного уравнения через k
Если у квадратного уравнения коэффициент bb четный, то можно решать уравнение через kk, при этом k=12bk = frac{1}{2} b.
Задача 5
Решим уравнение: −x2+2x+8=0.-x^2 + 2x + 8 = 0.
Обозначим коэффициенты:
a=−1a = -1,
b=2b = 2,
c=8c = 8
bb – четное.
k=12b=1k = frac {1}{2} b = 1.
Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac
D1=12–(−1)∗8=1+8=9=32D_1 = 1^2 – (-1) * 8 = 1 + 8 = 9 = 3^2
D1>0D_1 > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−k+D1)/ax_1 = (-k + {sqrt D}_1) / a
x2=(−k−D1)/ax_2 = (-k – {sqrt D}_1) / a
Подставляем численные значения:
x1=(−1+3)/(−1)=2/(−1)=−2x_1 = (-1 + 3) / (-1) = 2 / (-1) = -2
x2=(−1–3)/(−1)=−4/(−1)=4x_2 = (-1 – 3) / (-1) = -4 / (-1) = 4
Ответ: x_1 = -2, x_2 = 4.
Задача 6
Решим уравнение: 9×2–6x+1=0.9x^2 – 6x + 1 = 0.
Обозначим коэффициенты:
a=9a = 9,
b=−6b = -6,
c=1c = 1
bb – четное.
K=12b=−3.K = frac{1}{2} b = -3.
Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac
D1=(−3)2–9∗1=9–9=0D_1 = {(-3)}^2 – 9 * 1 = 9 – 9 = 0
D1=0D_1 = 0 – значит, уравнение имеет 1 корень.
Находим корень уравнения по следующей формуле: x=−k/ax = -k / a
Подставляем численные значения:
x=3/9=13x = 3 / 9 = frac{1}{3}
Ответ: x=13.x = frac{1}{3}.
Нахождение корней уравнения по теореме Виета
Если в квадратном уравнении a=1a = 1, то можно найти корни уравнения по теореме Виета.
Задача 7
Найдем корни уравнения: x2+3x+2=0.x^2 + 3x + 2 = 0.
Обозначим коэффициенты:
a=1a = 1,
b=3b = 3,
c=2c = 2.
Запишем 2 условия теоремы Виета:
x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c
Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа -2 и -1.
Значит, корни уравнения равны:
x1=−2x_1 = -2
x2=−1x_2 = -1
Ответ: x1=−2x_1 = -2, x2=−1x_2 = -1.
Задача 8
Найдем корни уравнения: x2–5x+6=0.x^2 – 5x +6 = 0.
Обозначим коэффициенты:
a=1a = 1,
b=−5b = -5,
c=6c = 6
Запишем 2 условия теоремы Виета:
x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c
Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа 2 и 3.
Значит, корни уравнения равны:
x1=2x_1 = 2
x2=3x_2 = 3
Ответ: x1=2x_1 = 2, x2=3.x_2 = 3.
Тест по теме «Примеры решения квадратных уравнений»
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Дискриминант
квадратного уравнения
Поддержать сайт![]()
Мы уже разобрали,
как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют
дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Запомните!
![]()
Выражение «b2 − 4ac», которое находится под корнем,
принято называть дискриминантом и обозначать буквой «D».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 = , где «D = b2 − 4ac»
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака «D» (дискриминанта)
квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
2x2 + 5x −7 = 0
D = b2 − 4ac
D = 52 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = 1 |
x2 = −3 |
| x1 = 1 |
x2 = −3 |
Ответ: x1 = 1;
x2 = −3
Вывод: когда «D > 0» в квадратном уравнении два корня.
II случай
D = 0
(дискриминант равен нулю)
16x2 − 8x + 1 = 0
D = b2 − 4ac
D = (−8)2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
x1;2 =
x1;2 =
x =
x =
Ответ: x =
Вывод: когда «D = 0» в квадратном уравнении один корень.
III случай
D < 0
(дискриминант меньше нуля)
9x2 − 6x + 2 = 0
D = b2 − 4ac
D = (−6)2 − 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
x1;2 =
x1;2 =
Ответ: нет действительных корней
Вывод: когда «D < 0» в квадратном уравнении нет корней.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Решение квадратных уравнений
6 июля 2011
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D < 0, корней нет;
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x2 − 8x + 12 = 0;
- 5x2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
![]()
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- 15 − 2x − x2 = 0;
- x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
![]()
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
[begin{align} & {{x}_{1}}=frac{2+sqrt{64}}{2cdot left( -1 right)}=-5; \ & {{x}_{2}}=frac{2-sqrt{64}}{2cdot left( -1 right)}=3. \ end{align}]
Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
[x=frac{-12+sqrt{0}}{2cdot 1}=-6]
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x2 + 9x = 0;
- x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
![]()
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a) < 0, корней нет.
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
![]()
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x2 − 7x = 0;
- 5x2 + 30 = 0;
- 4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Смотрите также:
- Теорема Виета

- Следствия из теоремы Виета

- Тест на тему «Значащая часть числа»

- Метод коэффициентов, часть 1

- Однородные тригонометрические уравнения: общая схема решения

- Задача B4: строительные бригады

На чтение 7 мин. Просмотров 7.5k.
Важная характеристика квадратных уравнений – их дискриминант. По значению этой величины определяют, сколько корней у данного уравнения и есть ли они.
В 8 классе по алгебре начинают изучать квадратные уравнения и самый популярный способ их решения – через дискриминант. Формула вычисления дискриминанта известна
![]()
Дискриминант в математике используется чтобы определить сколько корней в уравнении — 1 корень, 2 корня или действительных корней нет. В этой статье определим, что такое дискриминант и выведем формулу дискриминанта.
Определение
Определим что такое дискриминант и зачем он нужен в математике, а также как его рассчитать.
Дискриминантом называют число, описывающее свойство коэффициентов квадратного многочлена. Хотя есть дискриминанты и кубических многочленов.
По этому числу определяют характер корней уравнения, полученному если многочлен приравнять к нулю. Так, если дискриминант больше нуля, то уравнение будет иметь два корня, равен нулю, то 1 корень, а если будет меньше нуля, то корней не будет.
Дискриминант (определение) помогает определить наличие или отсутствие корней квадратного уравнения, не решая его.
Обозначается дискриминант квадратного уравнения буквой
или знаком Δ. И находится по формуле:
D=b^2-4ac , где
,
и
— коэффициенты уравнения:
ax^2+bx+c=0
Корни через дискриминант определяются по формулам:
displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}
Пример вычисления дискриминанта:
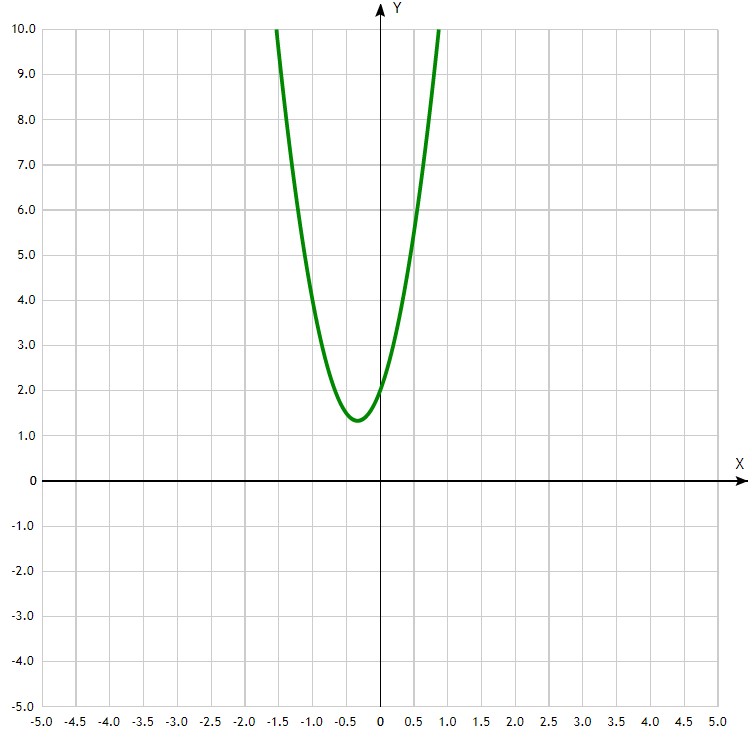
Вычислим дискриминант в уравнении 6x^2+4x+2=0 .
По формуле находим:
D=b^2-4ac=4^2-4cdot 6 cdot 2=16-48=-32
Мы получили отрицательный дискриминант, значит, данное уравнение не имеет действительных корней. Действительно, так как корни квадратного уравнения находят по формулам:
displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}
Подставим значения для исходного уравнения:
displaystyle x_1=frac{-4-sqrt{-32}}{12} и displaystyle x_2=frac{-4+sqrt{-32}}{12}
Как видим, мы никак не сможем посчитать корни — у нас отрицательное число под знаком радикала. И, действительно, если вы построите график функции f (x)=6x^2+4x+2 — он нигде не пересечет ось ![]() , то есть ни при каком
, то есть ни при каком ![]() мы не получим ноль.
мы не получим ноль.
![]()
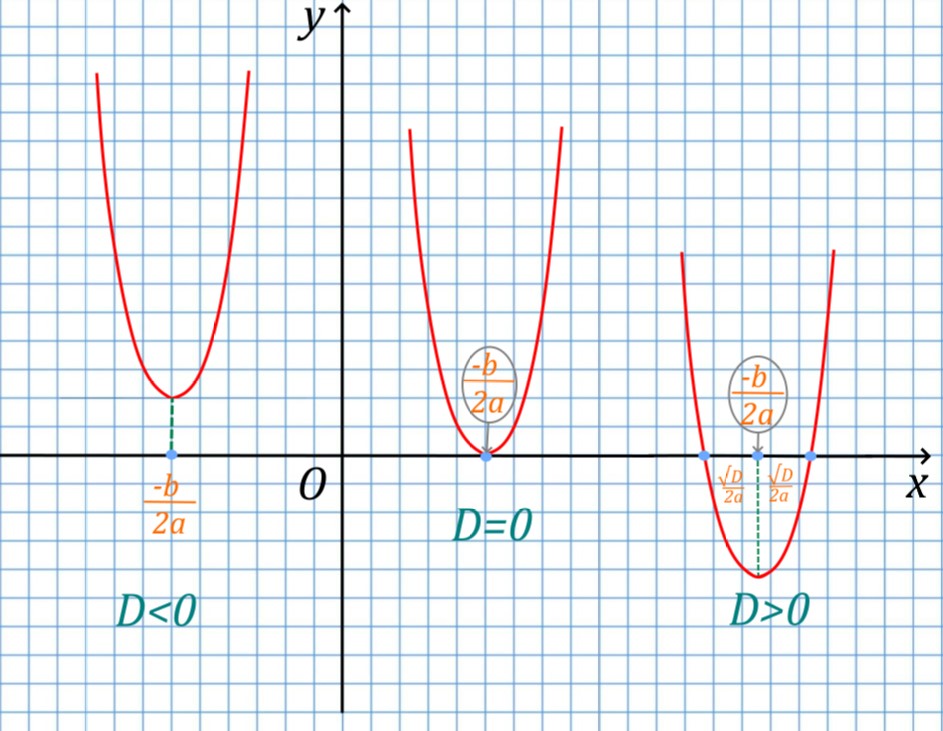
Геометрический смысл дискриминанта
Что означает дискриминант на графике, каков его геометрический смысл? Графически дискриминант квадратного уравнения характеризует расстояние по оси абсцисс между точкой — вершиной параболы (парабола — график квадратичной функции) и точкой пересечения графика с осью абсцисс. Посмотрите на рисунок. На нем видно:
- Если дискриминант равен нулю (D=0), это значит, что вершина параболы и является точкой пересечения с осью абсцисс — расстояние между точкой пересечения и вершиной параболы равно нулю.
- Когда D>0, то справа и слева от точки абсцисс вершины параболы на одинаковом расстоянии displaystyle frac{sqrt{D}}{2a} будут находиться точки пересечения параболы ax^2+bx+c=y, которые являются корнями уравнения ax^2+bx+c=0.
- Когда D<0 — это означает, что точек действительных отметить на оси абсцисс нельзя, то есть от вершины отложить расстояние до точек пересечения графика с осью абсцисс невозможно, то есть этих точек пересечения нет. График не пересекает ось абсцисс и корней уравнения [katex]ax^2+bx+c=0[/katex] нет.
Корни квадратного уравнения через дискриминант.
Полное квадратное уравнение
Пусть нам дано уравнение вида ax^2+bx+c=0. Вычисляем дискриминант по известной формуле. Затем определяем корни уравнения.
- Если D>0 получаем два вещественных корня displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}.
- Если D=0 корни будут совпадать: displaystyle x_1=x_2=frac{-b}{2a}
- Если D<0, вещественных корней нет, но есть мнимые корни или так называемые комплексные корни (обычно изучаются в курсе математического анализа в ВУЗах, хотя иногда и встречаются в алгебре 9-11 классов).
Неполное квадратное уравнение
Неполным называется такое квадратное уравнение, когда один из коэффициентов такого уравнения равен нулю.
- Пусть коэффициент a=0, тогда уравнение сводится к линейному уравнению вида kx+b=0 и уже не будет считаться неполным.
- Если равны нулю два коэффициента:
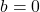 и
и 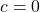 , тогда
, тогда 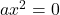 . Решением такого уравнения будет:
. Решением такого уравнения будет: 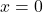 .
. - Если равен нулю коэффициент b, то имеем D=-4ac и displaystyle x_1= frac{sqrt{D}}{2a} и displaystyle x_2= -frac{sqrt{D}}{2a}.
- При равенстве нулю свободного члена c=0 имеем D=b^2 и displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}.
Приведенное квадратное уравнение
Приведенным квадратным уравнением называется такое уравнение вида ![]() , в котором старший коэффициент равен a=1. Оно решается обычно по теореме Виета.
, в котором старший коэффициент равен a=1. Оно решается обычно по теореме Виета.
Дискриминант находится по формуле: ![]() .
.
Если второй коэффициент кратен 2
Если коэффициент b можно разделить на 2 (с четным вторым коэффициентом), то тогда вычисляется не полный дискриминант, а displaystyle frac{D}{4} по формуле:
displaystyle frac{D}{4}=left ( frac{b}{2} right)^2-ac,
а корни: displaystyle x_1=frac{-frac{b}{2}-sqrt{frac{D}{4}}}{a} и второй корень displaystyle x_2=frac{-frac{b}{2}+sqrt{frac{D}{4}}}{a}.
Примеры нахождения корней уравнения с помощью дискриминанта
Пример 1
Решим уравнение: 4x^2+5x-5=0
Находим дискриминант: D=25-4 cdot 4 cdot (-5)=25+80=105
Корни: displaystyle x_1=frac{-5-sqrt{105}}{2cdot 4}, displaystyle x_2=frac{-5+sqrt{105}}{2cdot 4}
или
displaystyle x_1=frac{-5-sqrt{105}}{8}, displaystyle x_2=frac{-5+sqrt{105}}{8}
Пример 2
Сколько корней в данном уравнении 2x^2-3x+6=0?
Для ответа на этот вопрос необходимо найти дискриминант:
D=3^2-4 cdot 2 cdot 6=9-48=-39
D<0[/katex] — действительных корней нет.</p> <h3>Пример 3</h3> <p>[katex]x^2-6x-72=0 — найти корень.
D=b^2-4ac=(-6)^2-4 cdot (-72)=36+288=324
Так как ![]() , имеем два корня:
, имеем два корня:
displaystyle x_1=frac{6-sqrt{324}}{2}, x_2=frac{6+sqrt{324}}{2}
displaystyle x_1=frac{6-18}{2}=-6, x_2=frac{6+18}{2}=12
Пример 4
Решить неполное уравнение
x^2-4=0
Способ 1
Разложим левую часть по формуле разность квадратов:
(x-2)(x+2)=0
Тогда корни:
x_1=-2, x_2=2
Способ 2
Решим задачу с помощью дискриминанта: ![]() , тогда displaystyle x_1=sqrt{D}/2=sqrt{16}/2=4/2=2,
, тогда displaystyle x_1=sqrt{D}/2=sqrt{16}/2=4/2=2,
displaystyle x_2=-sqrt{D}/2=-sqrt{16}/2=-4/2=-2
Пример 5
Придумайте такое квадратное уравнение, в котором будет нулевой дискриминант.
Решение:
Так как формула дискриминанта: D=b^2-4ac, то выберем любые коэффициенты ![]() и
и ![]() , а
, а ![]() найдем, если приравняем D=b^2-4ac к нулю.
найдем, если приравняем D=b^2-4ac к нулю.
Пусть ![]() , a
, a ![]() , тогда displaystyle D=4^2-4cdot 7cdot c=0
, тогда displaystyle D=4^2-4cdot 7cdot c=0
4^2-4cdot 7cdot c=0
16-28c=0
-28c=-16 Разделим левую и правую части на -4.
7c=4
displaystyle c=frac{4}{7}
И, получаем: displaystyle 7x^2+4x+frac{4}{7}=0
Ответ: displaystyle 7x^2+4x+frac{4}{7}=0
Выводы
Самое важное, что надо запомнить, это формулу:
D=b^2-4ac
и как определяются корни квадратного уравнения:
displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}
Можно забыть, как определяются корни в разных видах квадратных уравнений, неполных, приведенных, но если вы знаете главное — как определяется дискриминант и корни в полном квадратном уравнении, то вы сможете решить любое уравнение второй степени.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье “Решение неполных квадратных уравнений”.
Какие же квадратные уравнения называются полными? Это уравнения вида ах2 + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b2 – 4ас .
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D < 0),то корней нет.
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х1 = (-b – √D)/2a , и х2 = (-b + √D)/2a .
Например. Решить уравнение х2 – 4х + 4= 0.
D = 42 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х2 + х + 3 = 0.
D = 12 – 4 · 2 · 3 = – 23
Ответ: корней нет.
Решить уравнение 2х2 + 5х – 7 = 0.
D = 52 – 4 · 2 · (–7) = 81
х1 = (-5 – √81)/(2·2)= (-5 – 9)/4= – 3,5
х2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1.
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 32 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах2, затем с меньшим – bx, а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х2 равен единице и уравнение примет вид х2 + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х2.
На рисунке 3 приведена схема решения приведенных квадратных уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 62 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х1 = (-6 – 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3
х2 = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D1 = 32 – 3 · (– 6) = 9 + 18 = 27
√(D1) = √27 = √(9 · 3) = 3√3
х1 = (-3 – 3√3)/3 = (3 (-1 – √(3)))/3 = – 1 – √3
х2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного  уравнения рисунок 3.
уравнения рисунок 3.
D2 = 22 – 4 · (– 2) = 4 + 8 = 12
√(D2) = √12 = √(4 · 3) = 2√3
х1= (-2 – 2√3)/2 = (2 (-1 – √(3)))/2 = – 1 – √3
х2= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
