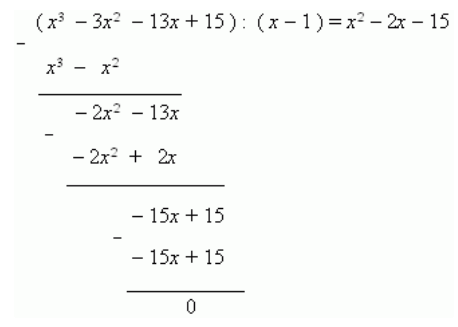Как найти дискриминант с кубом

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.

Кубическим уравнением называется уравнение вида

• ax³ + bx² + cx +d = 0 , (1)
• где a, b,c ,d – постоянные коэффициенты, а х – переменная.

Мы рассмотрим случай, когда коэффициенты являются веществеными числами.

Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.

Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.

Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:

Δ= -4b³d + b²c² – 4ac³ + 18abcd – 27a²d²  (Да, это дискриминант кубического уравнения)

Итак, возможны только 3 следующих случая:

• Δ > 0 – тогда уравнение имеет 3 различных корня. (Для продвинутых – три различных вещественных корня)
• Δ < 0 – уравнение имеет лишь 1 корень. (1 вещественный и пару комплексно сопряженных корней)
• Δ = 0 – хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)

На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.

Формула Кардано решения кубических уравнений (нахождения корней).

Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).

Канонической формой кубического уравнения называется уравнение вида

y³ + py + q = 0 (2)

К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:

• x= y – b/3a (3)
• p= – b²/3a² + c/a
• q= 2b³/27a³ – bc/3a² + d/a

Итак, приступим к вычислению корней. Найдем следующие величины:

• Q=(p/3)³ + (q/2)²
• α = (-q/2 + Q^1/2)^1/3
• β = (-q/2 – Q^1/2)^1/3

Дискриминант уравнения (2) в этом случае равен

Δ = – 108Q

Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:

• y₁= α + β
• y₂= – (α + β)/2 + (3^1/2(α – β)/2)i
• y₃ =- (α + β)/2 – (3^1/2(α – β)/2)i

Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y₁. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y₂, y₃ и подставьте их в (3).

Если Q<0, то уравнение (2), как и уравнение (1) имеет три различных вещественных корня, но для их вычисления нужно уметь извлекать квадратный корень из отрицательного числа. Если вы это умеете, то проделайте расчеты, получите три корня y₁, y₂, y₃ и подставьте их в (3).

Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем

• α = β, и
• y₁=2α,
• y₂= y₃ = – α.

Аналогично подставляем в (3) и получаем ответ.

Тригонометрическая формула Виета решения кубических уравнений (нахождения корней).

Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида

x³ + ax² + bx +c = 0 (4)

Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.

Итак, алгоритм применения этой формулы:

1. Вычисляем

• Q=(a²– 3b)/9
• R=(2a³ – 9ab + 27c)/54

2. Вычисляем

S = Q³ – R²

3. a) Если S>0, то вычисляем

φ=(arccos(R/Q^3/2))/3

И наше уравнение имеет 3 корня (вещественных):

• x₁= – 2(Q)^1/2cos(φ) – a/3
• x₂= – 2(Q)^1/2cos(φ+2π/3) – a/3
• x₃= – 2(Q)^1/2cos(φ-2π/3) – a/3

б) Если S<0, то заменим тригонометрические функции гиперболическими.

Вычисляем

φ=(Arch( |R|/|Q|^3/2)/3

Тогда единственный корень (вещественный): x₁= -2sgn(R)*|Q|^1/2*ch(φ) – a/3

Для тех, кого интересуют также и мнимые корни:

• x₂= sgn(R)*|Q|^1/2*ch(φ) – a/3 +(3|Q|)^1/2 sh(φ)i
• x₃= sgn(R)*|Q|^1/2*ch(φ) – a/3 -(3|Q|)^1/2sh(φ)i

ГДЕ:

• ch(x)=(e^x+e^-x)/2
• Arch(x) = ln(x + (x²-1)^1/2)
• sh(x)=(e^x-e^-x)/2
• sgn(x) – знак х

в) Если S=0,то уравнение имеет меньше трех различных решений:

• x₁= -2*R^1/3 – a/3
• x₂=x₃=R^1/3 – a/3

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.

Кубическим уравнением называется уравнение вида

• ax 3 + bx 2 + cx +d = 0 , (1)
• где a, b,c ,d – постоянные коэффициенты, а х – переменная.

Мы рассмотрим случай, когда коэффициенты являются веществеными числами.

Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.

Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.

Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:

Δ= -4b 3 d + b 2 c 2 – 4ac 3 + 18abcd – 27a 2 d 2 (Да, это дискриминант кубического уравнения)

Итак, возможны только 3 следующих случая:

• Δ > 0 – тогда уравнение имеет 3 различных корня. (Для продвинутых – три различных вещественных корня)
• Δ 3 + py + q = 0 (2)

К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:

• x= y – b/3a (3)
• p= – b 2 /3a 2 + c/a
• q= 2b 3 /27a 3 – bc/3a 2 + d/a

Итак, приступим к вычислению корней. Найдем следующие величины:

Дискриминант уравнения (2) в этом случае равен

Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:

Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y₁. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y₂, y₃ и подставьте их в (3).

Если Q 3 + ax 2 + bx +c = 0 (4)

Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.

Итак, алгоритм применения этой формулы:

3. a) Если S>0, то вычисляем

И наше уравнение имеет 3 корня (вещественных):

Тогда единственный корень (вещественный): x₁= -2sgn(R)*|Q| 1/2 *ch(φ) – a/3

Для тех, кого интересуют также и мнимые корни:

• ch(x)=(e x +e -x )/2
• Arch(x) = ln(x + (x 2 -1) 1/2 )
• sh(x)=(e x -e -x )/2
• sgn(x) – знак х

в) Если S=0,то уравнение имеет меньше трех различных решений:

Консультации и техническая
поддержка сайта: Zavarka Team

Решение кубических уравнений

Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.

Решение двучленного кубического уравнения вида A x 3 + B = 0

Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что

x 3 + B A = 0 x + B A 3 x 2 – B A 3 x + B A 2 3 = 0

Результат первой скобки примет вид x = – B A 3 , а квадратный трехчлен – x 2 – B A 3 x + B A 2 3 , причем только с комплексными корнями.

Найти корни кубического уравнения 2 x 3 – 3 = 0 .

Решение

Необходимо найти х из уравнения. Запишем:

2 x 3 – 3 = 0 x 3 – 3 2 = 0

Необходимо применить формулу сокращенного умножения. Тогда получим, что

x 3 – 3 2 = 0 x – 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0

Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.

Ответ: x = 3 3 2 6 .

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0

Вид квадратного уравнения – A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что

A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 – x + 1 + B x x + 1 = x + 1 A x 2 + x B – A + A

Корень уравнения равен х = – 1 , тогда для получения корней квадратного трехчлена A x 2 + x B – A + A необходимо задействовать через нахождение дискриминанта.

Решить уравнение вида 5 x 3 – 8 x 2 – 8 x + 5 = 0 .

Решение

Уравнение является возвратным. Необходимо произвести группировку. Получим, что

5 x 3 – 8 x 2 – 8 x + 5 = 5 x 3 + 1 – 8 x 2 + x = = 5 x + 1 x 2 – x + 1 – 8 x x + 1 = x + 1 5 x 2 – 5 x + 5 – 8 x = = x + 1 5 x 2 – 13 x + 5 = 0

Если х = – 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 – 13 x + 5 :

5 x 2 – 13 x + 5 = 0 D = ( – 13 ) 2 – 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 – 69 2 · 5 = 13 10 – 69 10

Ответ:

x 1 = 13 10 + 69 10 x 2 = 13 10 – 69 10 x 3 = – 1

Решение кубических уравнений с рациональными корнями

Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .

Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .

Решение

3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0

Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что

D = 4 2 – 4 · 3 · 2 = – 8 . Так как его значение отрицательное, то корней трехчлена нет.

Ответ: х = 0 .

Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :

A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2

Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x – x 1 . Тогда сможем найти корни квадратного трехчлена.

Найти корни заданного уравнения 2 x 3 – 11 x 2 + 12 x + 9 = 0 .

Решение

Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что

2 x 3 – 11 x 2 + 12 x + 9 = 0 2 3 x 3 – 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 – 11 y 2 + 24 y + 36 = 0

Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:

± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36

Необходимо произвести подстановку y 3 – 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида

1 3 – 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( – 1 ) 3 – 11 · ( – 1 ) 2 + 24 · ( – 1 ) + 36 = 0

Отсюда видим, что у = – 1 – это корень. Значит, x = y 2 = – 1 2 .

Далее следует деление 2 x 3 – 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:

x i	Коэффициенты многочлена
2	– 11	12	9
– 0 . 5	2	– 11 + 2 · ( – 0 . 5 ) = – 12	12 – 12 · ( – 0 . 5 ) = 18	9 + 18 · ( – 0 . 5 ) = 0

2 x 3 – 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 – 12 x + 18 = = 2 x + 1 2 x 2 – 6 x + 9

После чего необходимо найти корни квадратного уравнения вида x 2 – 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 – 6 x + 9 = x – 3 2 , где х = 3 будет его корнем.

Ответ: x 1 = – 1 2 , x 2 , 3 = 3 .

Алгоритм можно применять для возвратных уравнений. Видно, что – 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.

Решение кубических уравнений по формуле Кардано

Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .

После чего p = – B 1 2 3 + B 2 и q = 2 B 1 3 27 – B 1 B 2 3 + B 3 .

Полученные p и q в формулу Кардано. Получим, что

y = – q 2 + q 2 4 + p 3 27 3 + – q 2 – q 2 4 + p 3 27 3

Подбор кубических корней должен удовлетворять на выходе значению – p 3 . Тогда корни исходного уравнения x = y – B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.

Найти корни заданного уравнения 2 x 3 – 11 x 2 + 12 x + 9 = 0 .

Решение

Видно, что A 0 = 2 , A 1 = – 11 , A 2 = 12 , A 3 = 9 .

Необходимо найти B 1 = A 1 A 0 = – 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .

Отсюда следует, что

p = – B 1 2 3 + B 2 = – – 11 2 2 3 + 6 = – 121 12 + 6 = – 49 12 q = 2 B 1 3 27 – B 1 B 2 3 + B 3 = 2 · – 11 2 3 27 – – 11 2 · 6 3 + 9 2 = 343 108

Производим подстановку в формулу Кордано и получим

y = – q 2 + q 2 4 + p 3 27 3 + – q 2 – – q 2 4 + p 3 27 3 = = – 343 216 + 343 2 4 · 108 2 – 49 3 27 · 12 3 3 + – 343 216 – 343 2 4 · 108 2 – 49 3 27 · 12 3 3 = = – 343 216 3 + – 343 216 3

– 343 216 3 имеет три значения. Рассмотрим их ниже.

– 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2

Если k = 0 , тогда – 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2

Если k = 1 , тогда – 343 216 3 = 7 6 cosπ + i · sinπ = – 7 6

Если k = 2 , тогда – 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 – i · 3 2

Необходимо произвести разбиение по парам, тогда получим – p 3 = 49 36 .

Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 – i · 3 2 , – 7 6 и – 7 6 , 7 6 1 2 – i · 3 2 и 7 6 1 2 + i · 3 2 .

Преобразуем при помощи формулы Кордано:

y 1 = – 343 216 3 + – 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 – i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = – 343 216 3 + – 343 216 3 = – 7 6 + – 7 6 = – 14 6 y 3 = – 343 216 3 + – 343 216 3 = = 7 6 1 2 – i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6

x 1 = y 1 – B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 – B 1 3 = – 14 6 + 11 6 = – 1 2 x 3 = y 3 – B 1 3 = 7 6 + 11 6 = 3

Ответ: x 1 = – 1 2 , x 2 , 3 = 3

При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.

Примеры решений кубических уравнений

Обзор методов решения кубических уравнений приведен на странице “Решение кубических уравнений”. Здесь мы приводим два примера, используя формулы Кардано и Виета.

Пример решения кубического уравнения с комплексными корнями

Решить кубическое уравнение:
(1.1) .

Решение

Поиск целых корней

Уравнение (1.1) имеет целые коэффициенты. Проверим, не содержит ли это уравнение целых корней. Член без – это 1. У числа 1 есть два делителя: 1 и – 1 . Подставим в уравнение (1.1) и . Ни для одного из этих чисел уравнение не выполняется. Следовательно, целых корней нет.

Сведение уравнения к приведенному виду

Пусть обозначают коэффициенты при , и свободный член. Делаем подстановку
(1.2) .
В результате получаем уравнение приведенного вида:
(1.3) ,
где
;
.

Определение вида корней

Определяем, имеет ли уравнение комплексные корни. Для этого находим дискриминант:
.
Дискриминант положителен. Следовательно, уравнение имеет один действительный корень и два комплексно сопряженных.

Нахождение корней по формуле Кардано

Поскольку дискриминант положителен, то находим корни по формуле Кардано:
, ,
где
; ; .
При , для величин и , можно взять действительные значения корней. Тогда соотношение выполняется автоматически.

Итак, мы нашли корни неполного кубического уравнения. По формуле (1.2) находим корни исходного уравнения:
.

Ответ

Пример с действительными корнями

Решить кубическое уравнение:
(2.1) .

Решение

Поиск целых корней

Уравнение (2.1) имеет целые коэффициенты. Проверим, нет ли у этого уравнения целых корней. Свободный член – это 1. У него есть два делителя: 1 и – 1 . Подставим в уравнение (2.1) и . Уравнение не выполняется ни для одного из этих чисел. Следовательно, целых корней нет.

Сведение уравнения к приведенному виду

В исходном уравнении (2.1),
.
Делаем подстановку
(2.2)
и приводим уравнение (2.1) к приведенному (неполному) виду:
(2.3) ,
где
;
.

Определение вида корней

Определяем, имеет ли уравнение комплексные корни. Находим дискриминант:
.
Дискриминант отрицателен. Следовательно, уравнение имеет три действительных корня.

Нахождение корней по формуле Виета

Итак, мы нашли корни приведенного кубического уравнения. По формуле (2.2) находим корни исходного уравнения:
.

Ответ

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Автор: Олег Одинцов . Опубликовано: 02-10-2016

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/systems/reshenie-kubicheskih-uravnenij/

http://1cov-edu.ru/mat_analiz/funktsii/ratsionalnye/mnogochleny/kubicheskie-uravneniya/primery/

[/spoiler]

Рада приветствовать всех на своем канале!

Сегодня поговорим о важной теме – кубических уравнениях и способах их решений. В школах им несправедливо уделяется куда меньшее внимание по сравнению с другими типами уравнений (конечно же, я намекаю на линейные и квадратные ;)). Однако на экзаменах и олимпиадах без навыка решения кубических уравнений обойтись практически невозможно.

На ОГЭ, например, уравнения данного типа периодически встречаются в самом первом номере второй части. На ЕГЭ умение раскладывать кубический многочлен на множители может понадобиться в номерах 13, 15 или 18. Про олимпиады и говорить нечего: навык решения уравнений третьей степени просто необходим всем, кто хочет быть в призерах!

Ну что, начнём???

Кубическое уравнение имеет общий вид:

Рассмотрим 3 возможных способа его решения.

1-й способ – группировка

В отдельных случаях при удачном подборе коэффициентов с помощью группировки удается разложить кубический многочлен на множители, после чего легко находятся все корни уравнения.

Внимание! Любое кубическое уравнение всегда имеет от одного до трех действительных корней.

Рассмотрим пример, в котором удобно сгруппировать первое и третье слагаемые, а также второе и четвертое:

откуда находим, что уравнение имеет единственный корень x = 2,
так как вторая скобка при любом значении x принимает исключительно положительные значения.

Но в самом общем случае коэффициенты уравнения могут быть подобраны менее удачно, тогда решить его подобным способом не получится. В этом случае применим следующий алгоритм.

Более универсальный 2-й способ

• Ищем такой x, при котором вся левая часть уравнения обращается в ноль, т.е. находим подбором первый корень x_1. Практически всегда подходит одно из чисел: 1, 2, 3, 4, -1, -2, -3, -4, 0.5, -0.5.
• Производим операцию деления многочлена на многочлен в столбик: делим исходный кубический многочлен на(x−x_1),
  где x_1 – корень, найденный в предыдущем пункте. В результате деления получаем квадратичную функцию, корни которой находятся без труда (дискриминант или теорема Виета всем в помощь).
• В ответ записываем корень x_1 и корни квадратичной функции, найденной во 2-м пункте.

Пример:

подбором находим, что корнем уравнения является число 1, т.е. y_1=1. Далее в столбик делим кубический четырехчлен, стоящий в левой части уравнения, на y−1 и получаем квадратичную функцию

Приравниваем её к нулю, решаем квадратное уравнение и находим еще два корня. В данном случае это числа 2 и 1. Таким образом, весь кубический многочлен можно записать в виде произведения:

Теперь прекрасно видно, что корнями исходного кубического уравнения являются числа 1 и 2, причем корень 1 имеет кратность, равную двум!

А как быть, если первый корень не находится подбором?

В этом случае помочь может только одно…

3-й способ – формула Кардано

Эта формула 100% сможет расколоть любое кубическое уравнение, даже с самыми страшными коэффициентами! Правда, есть у неё один минус… Она громоздкая и сложная. Настолько, что порой Вы задумаетесь, а так ли сильно хотите решить рассматриваемое уравнение 🙂

Если не испугались, то делюсь полезной ссылкой, по которой Вы сможете подробно ознакомиться с формулой Кардано, её выводом и примерами использования.

Именно эта формула, а точнее целый набор формул, находится внутри всех компьютерных программ, которые за считанные доли секунды способны выдать корни кубического уравнения. Однако, на экзаменах и олимпиадах полагаться приходится только на себя – никаких калькуляторов и прочих чудес техники…

В заключении статьи хочу предложить Вам проверить свои силы и закрепить пройденный материл. Для этого я приготовила три кубических уравнения. Попробуйте решить их разными способами 😉 Ответы жду в комментариях!

До скорых встреч!

P.s. На канале есть и другие публикации, которые могут быть Вам интересны:

Простые советы для успешной сдачи ЕГЭ по математике.

Разбираем самое “опасное” уравнение из первой части ЕГЭ по математике.

Лиге чемпионов посвящается. Подборка задач из ЕГЭ по математике с футбольным сюжетом.

Всё ли Вы знаете о ЕГЭ по математике?

ЕГЭ по математике 2020. Как это было. Подводим итоги.

Топ-5 отличий потенциального СТОбалльника ЕГЭ от обычного школьника

ЕГЭ 2021. Что год грядущий нам готовит.

В уравнении такого типа a не равно 0, вместо b,c,d могут быть любые однозначные числа.

Данный вид уравнения имеет как минимум один корень – y₁.

Решение таких равнений может осуществляться разными способами. Оно может преобразовываться в стандартное квадратное уравнение. В таком случае предстоит выбрать один из трех вариантов решения квадратного уравнения:

• разложение на множители;
• применение формул для квадратных уравнений;
• метод дополнения.

Решение кубических уравнений может осуществляться посредством формулы Кардано, а также теоремы Виета. Теорема Виета применяется для решения последней, четвертой степени.

Решение кубических уравнений с двумя членами

Деление на a предполагает вместо нее любую цифру, кроме 0. После преобразования можно применить формулы для решения кубических уравнений, например, сокращенного умножения суммы кубов:

y3=b/a=0

(y+³√b/a)(y²—³√b/a*y+³√(b/a)²)=0

В результате из первой скобки выводим:

y=-³√b/a

во второй скобке получаем выражение – трехчлен:

y2-3√b/a*y+3√(b/a)2

Методы решения кубических уравнений возвратного вида

Первым делом при решении таких уравнений в математике выполняется группировка:

ay3+by2+by+a=a(y³+1)+b(y²+y)=a(y+1)(y²-y+1)+by(y+1)=(y+1)(ay²+y(b-a)+a)

В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay²+y(b-a)+a, потребуется найти дискриминант.

Решение кубических уравнений в составе которых рациональные корни

Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:

ay³+by²+cy+d=0

При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:

ay3+by2+cy=0

Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:

y(ay²+by+c)=0

Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:

5y³+2y²+4y=0

Решение:

Первым делом стоит упростить уравнение.

5y³+2y²+4y=0

Получим уравнение вида:

y(5y²+2y+4)=0

y=0, так как является корнем выражения.

Следующий шаг – поиск корней квадратного трехчлена 5y²+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.

В ходе решения кубического уравнения с дискриминантом получим:

D=2²-2*5*4=-38

Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.

Если в уравнениях вида ay³+by²+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.

В случае, когда a не равно 0, при умножении на a² каждой составляющей уравнения происходит замещение переменных, и получается: x=ay

ay³+by²+cy+d=0

Каждую составляющую выражения умножаем на a²:

a³*y³+b*a²*y²+c*a*a*y+d*a²=0

Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:

x²+b*x²+c*a*x+d*a²

Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x₁ будет корнем, и в то же время корнем начального уравнения:

x₁=y₁/a

Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y_1.

Рассмотрим решение кубических уравнений такого вида на примере.

Пример:

Решить уравнение [x 3-3 x 2-13 x+15=0].

Решение:

Ищем первый корень перебором чисел: [0, pm1, pm2, pm3, pm5, pm15] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:

Теперь, решая квадратное уравнение: [x 2-2 x-15=0], находим оставшиеся два корня: x1=-3 и x2=5.

Ответ: 1; -3; 5.

Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений. Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.

Решение кубического уравнения с помощью формулы Кардано

Есть еще один способ — формула Кардано для решения кубических уравнений.

Если взять уравнение вида B₀y³+B₁y²+B₂y+B₃=0, то A₁=B₁/B₀, A₂=B₂/B₀, A₃=B₃/B₀.

Z=-A²₁/3+A₂

P=2A³₁/27-A₁A₂/3+A₃.

Выведенные значение Z и P подставим в формулу Кардано.

X=³√-P/2+√P²/4+Z³/27+³√-P/2-+√P2/4+Z3/27

В итоге подбор кубических корней должен соответствовать значению –Z/3. В этом случае корни исходного уравнения будут выглядеть следующим образом:

y=x-A₁/3

Применить формулу Кордано можно на примере для наглядности.

В данном случае для корней начального уравнения мы получим:

x₁=y₁-2=3-2=1;

x₂=y₂-2=-3-2=-5;

x₃=y₃-2=0-2=-2.

Получаем ответы: 1, -5, -2.

Общее решение кубического уравнения, если известен один из корней

За исходное уравнение возьмем следующее:

y³+ay²+by+c=0

Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y₁. В таком случае, если произвести деление начального уравнения y³+ay²+by+c=0 на y-y₁ получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y₂ и y₃.

Чтобы доказать это, преобразуем кубический многочлен следующим образом:

y₃+ay₂+by+c=(y-y₁)(y-y₂)(y-y₃)

При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.

Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.

Была ли эта статья полезной?