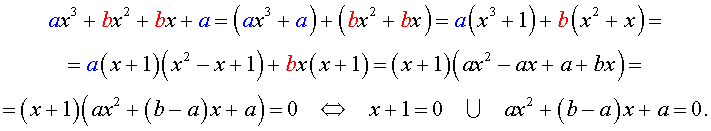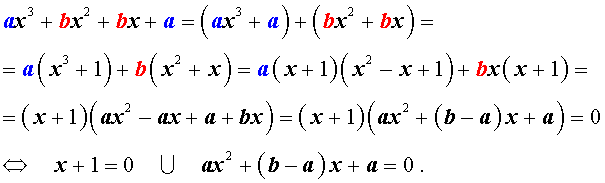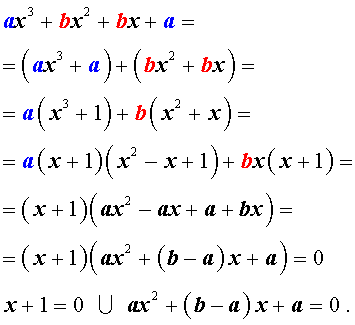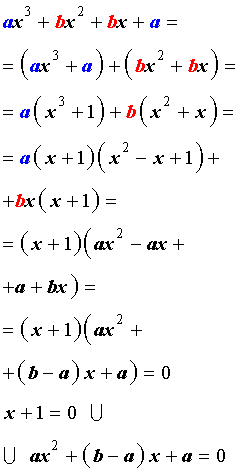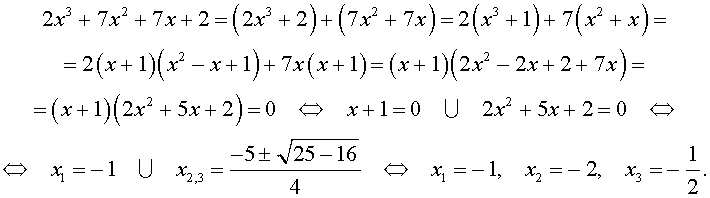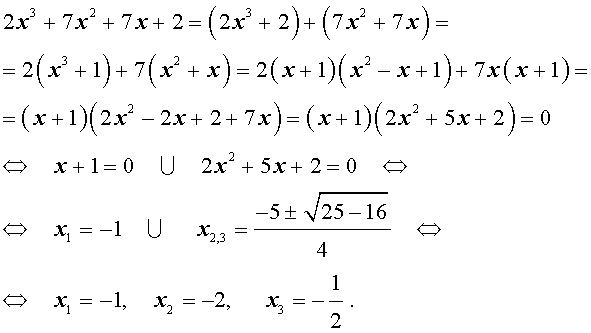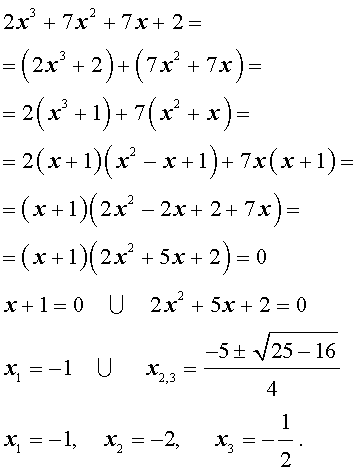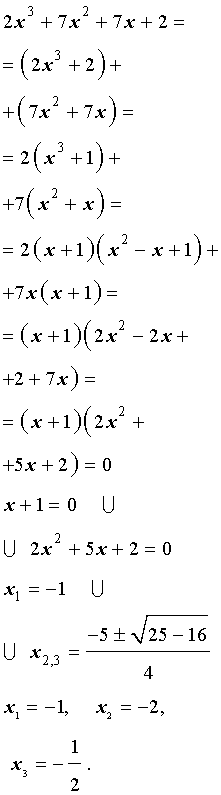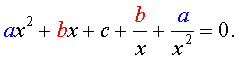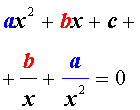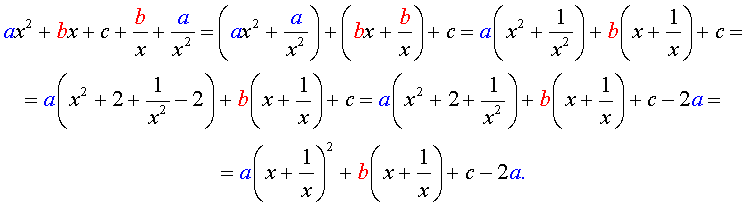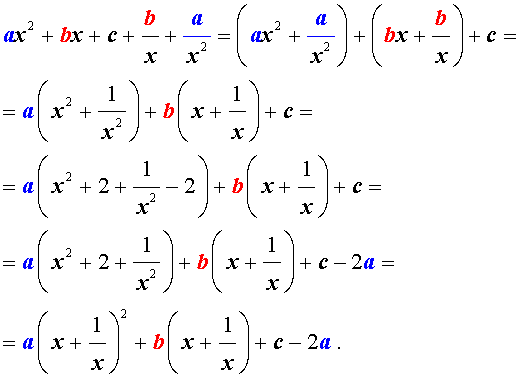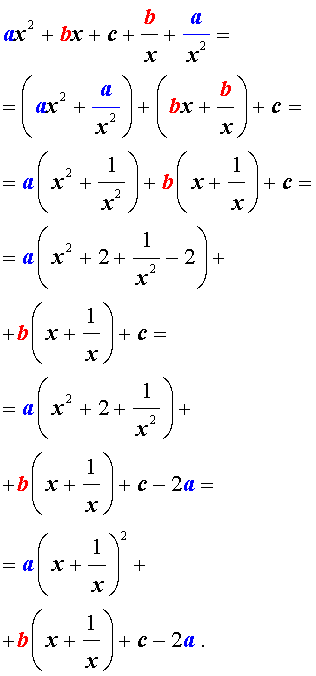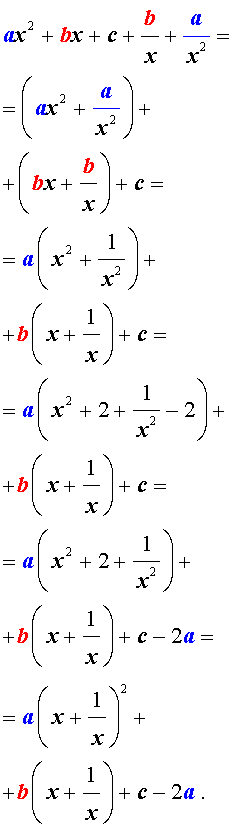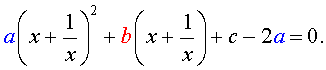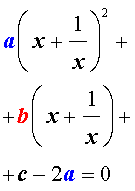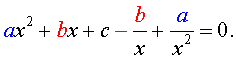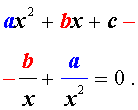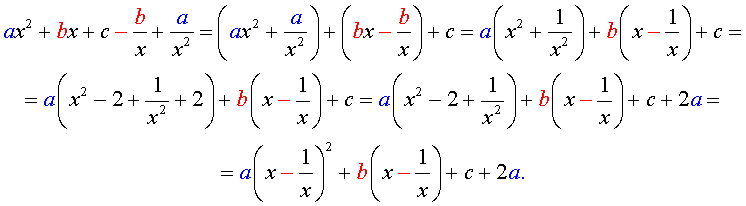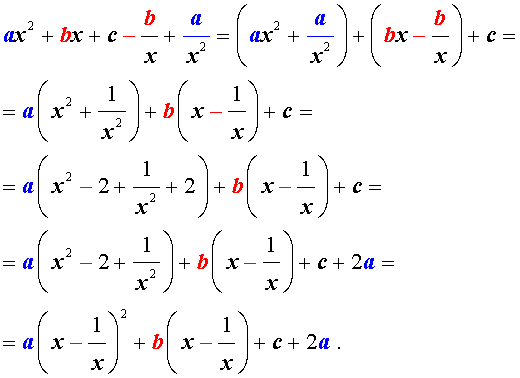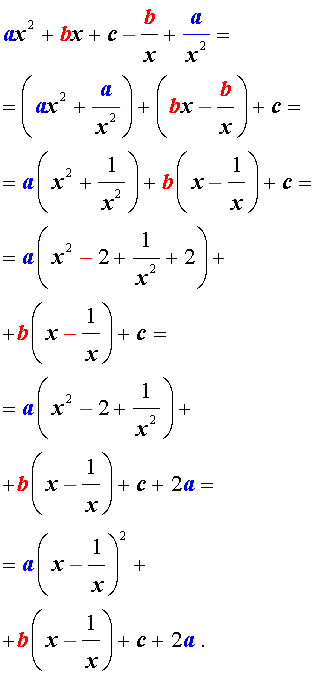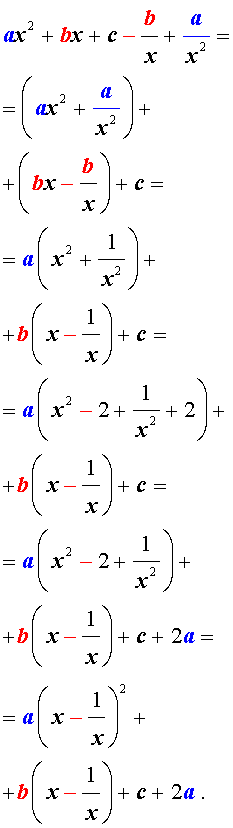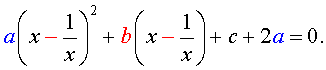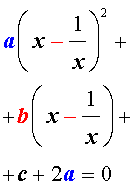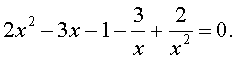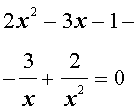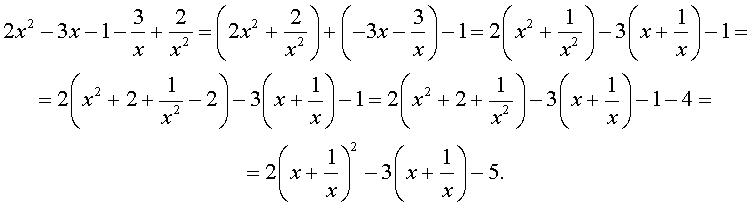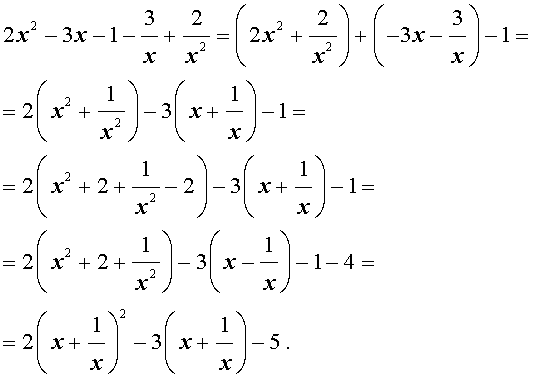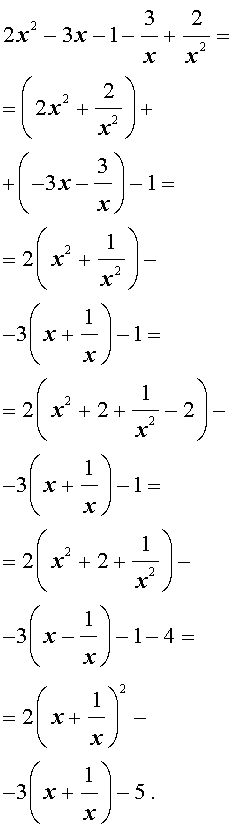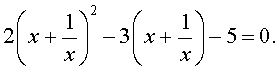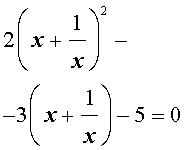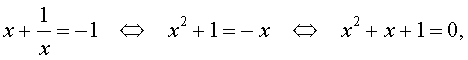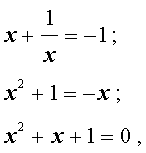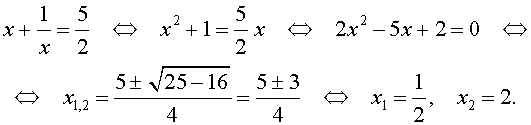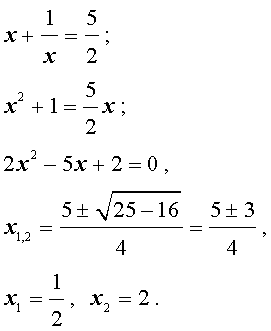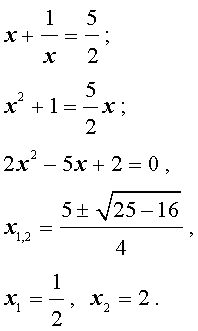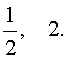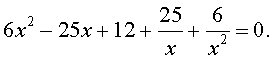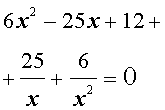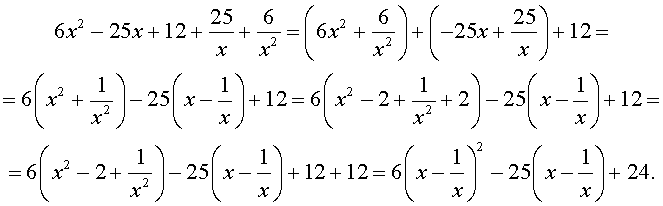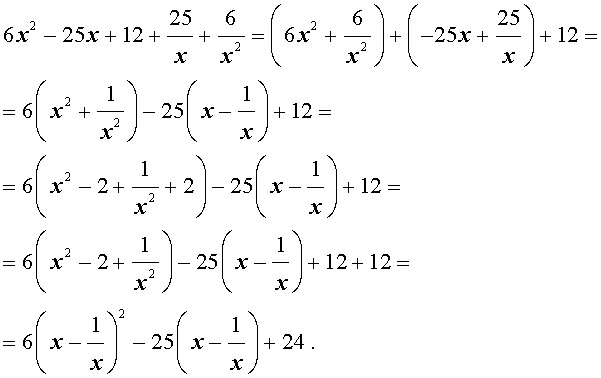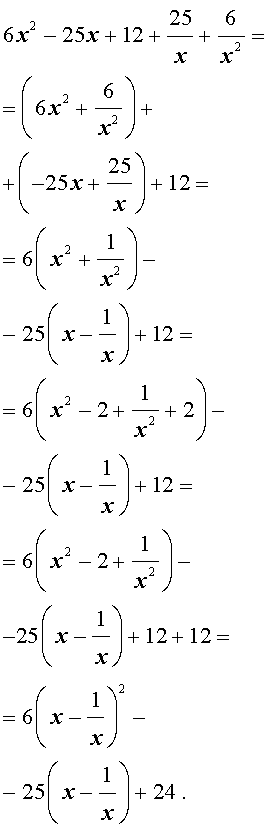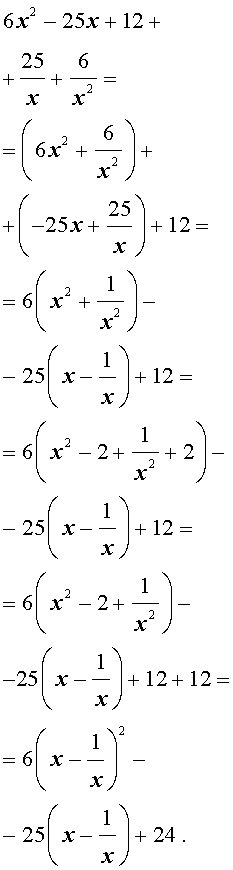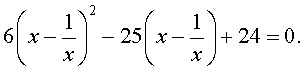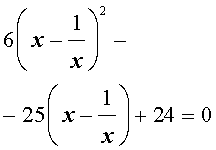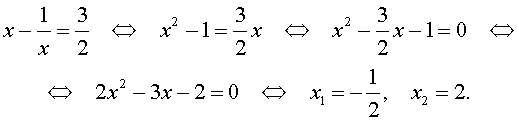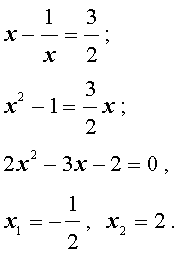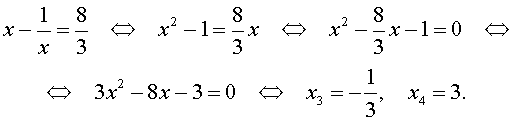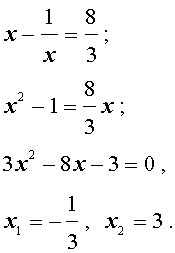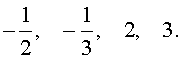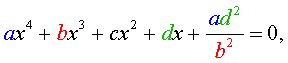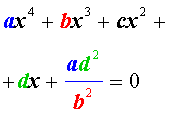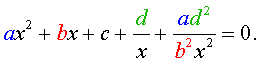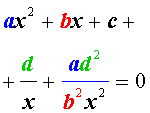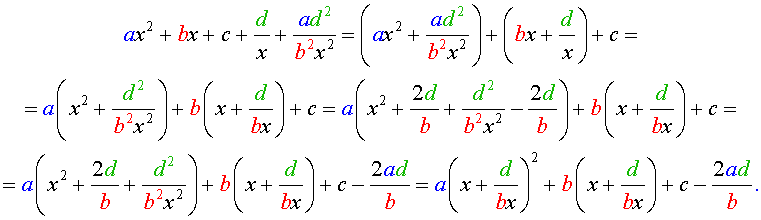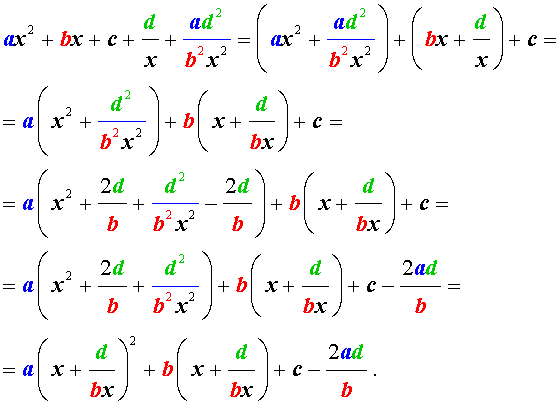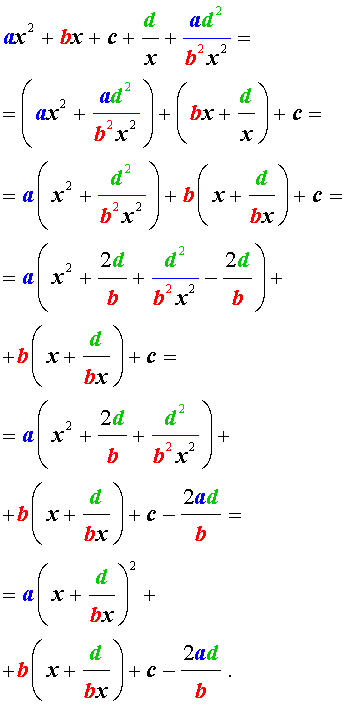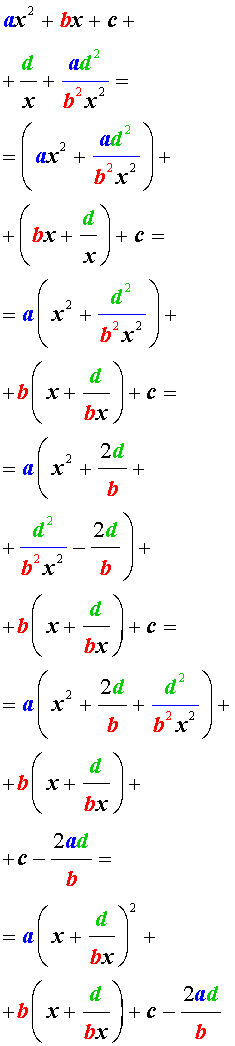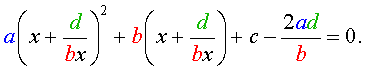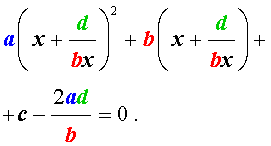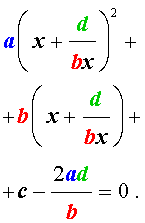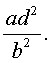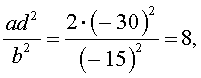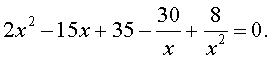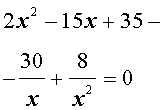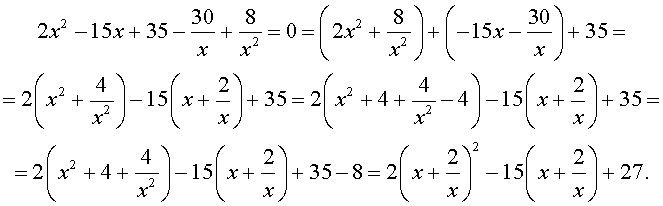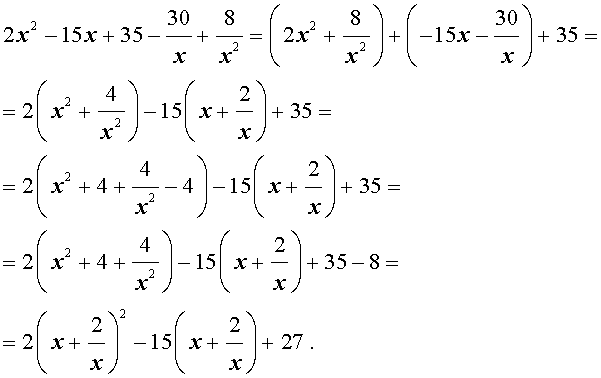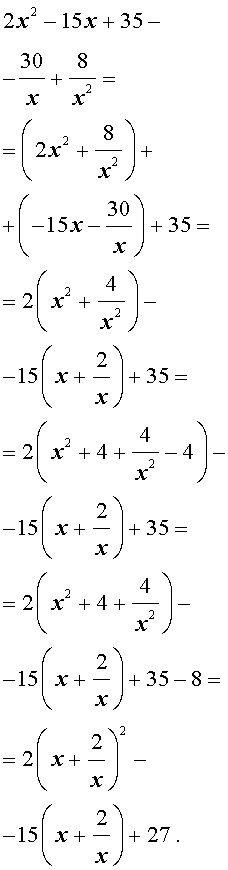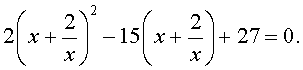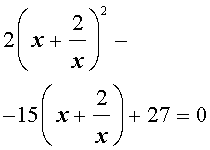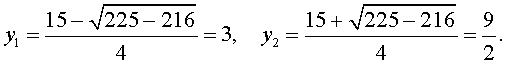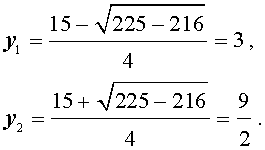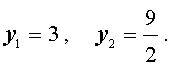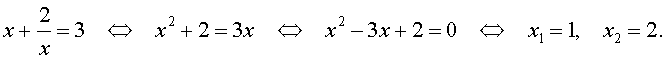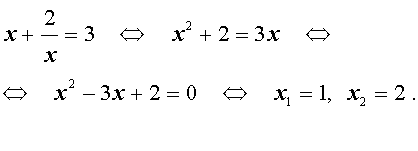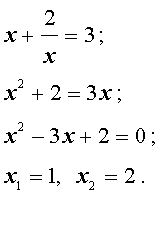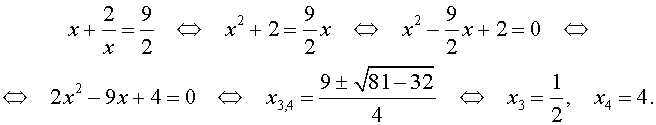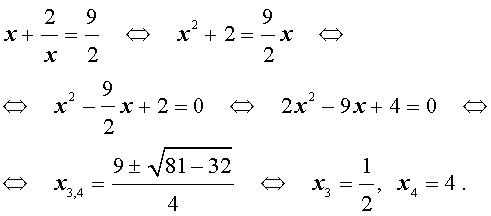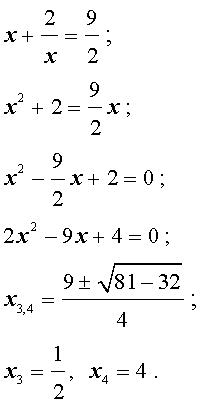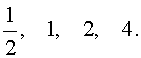Как найти дискриминант уравнения 4 степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид Ax4+B=0.

Остается лишь найти корни квадратных трехчленов.

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид Ax4+Bx3+Cx2+Bx+A=0

х=0 не является корнем этого уравнения: A·04+B·03+C·02+B·0+A=A≠0. Поэтому на x2 можно смело разделить обе части этого уравнения:

Ax4+Bx3+Cx2+Bx+A=0Ax2+Bx+C+Bx+Ax2=0Ax2+Ax2+Bx+Bx+C=0Ax2+1×2+Bx+1x+C=0

Проведем замену переменных x+1x=y⇒x+1×2=y2⇒x2+1×2=y2-2:

Ax2+1×2+Bx+1x+C=0A(y2-2)+By+C=0Ay2+By+C-2A=0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид Ax4+Bx2+C=0. Мы можем свести такое уравнение к квадратному Ay2+By+C=0 путем замены y=x2. Это стандартный прием.

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x4+Ax3+Bx2+Cx+D=0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y0. Это любой из корней кубического уравнения y3-By2+AC-4Dy-A2D+4BD-C2=0. После этого необходимо решить два квадратных уравнения x2+A2x+y02+A24-B+y0x2+A2y0-Cx+y024-D=0, у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Уравнения, сводящиеся к квадратным уравнениям:
возвратные (симметричные) уравнения

Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.

К таким уравнениям, в частности, относятся уравнения следующих типов:

Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .

Возвратные (симметричные) уравнения 3-ей степени

Возвратным уравнением 3-ей степени называют уравнение вида

a x 3 + b x 2 + b x + a = 0,

(1)

где a , b – заданные числа.

Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:

Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение

Пример 1 . Решить уравнение

2x 3 + 7x 2 + 7x + 2 = 0.

(2)

Решение . Разложим левую часть уравнения (2) на множители:

Ответ :.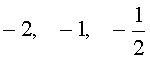

Возвратные (симметричные) уравнения 4-ой степени

Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида

a x 4 + b x 3 + cx 2 + + b x + a = 0,

(3)

а также уравнения вида

a x 4 + b x 3 + cx 2 – – b x + a = 0,

(4)

Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение

Преобразуем левую часть уравнения (5):

В результате этого преобразования уравнение (5) принимает вид

Если теперь обозначить

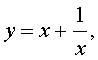(7)

то уравнение (6) станет квадратным уравнением:

a y 2 + b y + c – 2 a = 0.

(8)

Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .

Описание метода решения уравнений вида (3) завершено.

Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение

Преобразуем левую часть уравнения (9):

В результате этого преобразования уравнение (9) принимает вид

Если теперь обозначить

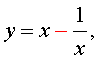(11)

то уравнение (10) станет квадратным уравнением:

a y 2 + b y + c + 2 a = 0.

(12)

Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .

Описание метода решения уравнений вида (4) завершено.

Пример 2 . Решить уравнение

2x 4 – 3x 3 – x 2 – – 3x + 2 = 0.

(13)

Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение

Преобразуем левую часть уравнения (14):

В результате этого преобразования уравнение (14) принимает вид

Если теперь обозначить

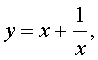(16)

то уравнение (15) станет квадратным уравнением:

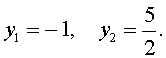(18)

В первом случае из равенства (16) получаем уравнение:

которое решений не имеет.

Во втором случае из равенства (16) получаем:

Ответ :

Пример 3 . Решить уравнение

6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0.

(19)

Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение

Преобразуем левую часть уравнения (20):

В результате этого преобразования уравнение (20) принимает вид

Если теперь обозначить

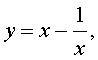(22)

то уравнение (21) станет квадратным уравнением:

6y 2 – 25y + 24 = 0.

(23)

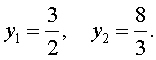(24)

В первом случае из равенства (22) получаем:

Во втором случае из равенства (22) получаем:

Ответ :

Обобщенные возвратные уравнения 4-ой степени

Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида

где a , b , c, d – заданные числа.

Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение

Преобразуем левую часть уравнения (26):

В результате этого преобразования уравнение (26) принимает вид

Если теперь обозначить

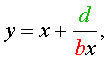(28)

то уравнение (27) станет квадратным уравнением:

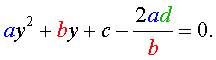(29)

Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .

Описание метода решения уравнений вида (25) завершено.

Пример 4 . Решить уравнение

2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0.

(30)

Решение . Введем для коэффициентов уравнения (30) следующие обозначения

и найдем значение выражения

то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение

Преобразуем левую часть уравнения (31):

В результате этого преобразования уравнение (31) принимает вид

Если теперь обозначить

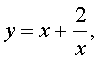(33)

то уравнение (32) станет квадратным уравнением:

2y 2 – 15y + 27 = 0.

(34)

В первом случае из равенства (33) получаем:

Во втором случае из равенства (33) получаем:

Ответ :

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .

Для решения этого типа уравнений применяются формулы сокращенного умножения:

A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A – 2 B A x 2 = 0 x 2 + B A 2 – 2 B A x 2 = 0 x 2 – 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0

Остается лишь найти корни квадратных трехчленов.

Решить уравнение четвертой степени 4 x 4 + 1 = 0 .

Решение

Для начала проведем разложение многочлена 4 x 4 + 1 на множители:

4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 – 4 x 2 = 2 x 2 – 2 x + 1 ( 2 x 2 + 2 x + 1 )

Теперь найдем корни квадратных трехчленов.

2 x 2 – 2 x + 1 = 0 D = ( – 2 ) 2 – 4 · 2 · 1 = – 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 – D 2 · 2 = 1 2 – i

2 x 2 + 2 x + 1 = 0 D = 2 2 – 4 · 2 · 1 = – 4 x 3 = – 2 + D 2 · 2 = – 1 2 + i x 4 = – 2 – D 2 · 2 = – 1 2 – i

Мы получили четыре комплексных корня.

Ответ: x = 1 2 ± i и x = – 1 2 ± i .

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0

х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:

A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0

Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 – 2 :

A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 – 2 ) + B y + C = 0 A y 2 + B y + C – 2 A = 0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :

2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0

2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0

Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 – 2

2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 – 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0

Решим полученное квадратное уравнение:

D = 2 3 + 2 2 – 4 · 2 · 6 = 12 + 4 6 + 2 – 8 6 = = 12 – 4 6 + 2 = 2 3 – 2 2 y 1 = – 2 3 – 2 + D 2 · 2 = – 2 3 – 2 + 2 3 – 2 4 = – 2 2 y 2 = – 2 3 – 2 – D 2 · 2 = – 2 3 – 2 – 2 3 + 2 4 = – 3

Вернемся к замене: x + 1 x = – 2 2 , x + 1 x = – 3 .

Решим первое уравнение:

x + 1 x = – 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 – 4 · 2 · 2 = – 14 x 1 = – 2 – D 2 · 2 = – 2 4 + i · 14 4 x 2 = – 2 – D 2 · 2 = – 2 4 – i · 14 4

Решим второе уравнение:

x + 1 x = – 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 – 4 · 1 · 1 = – 1 x 3 = – 3 + D 2 = – 3 2 + i · 1 2 x 4 = – 3 – D 2 = – 3 2 – i · 1 2

Ответ: x = – 2 4 ± i · 14 4 и x = – 3 2 ± i · 1 2 .

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.

Решить биквадратное уравнение 2 x 4 + 5 x 2 – 3 = 0 .

Решение

Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:

2 y 2 + 5 y – 3 = 0 D = 5 2 – 4 · 2 · ( – 3 ) = 49 y 1 = – 5 + D 2 · 2 = – 5 + 7 4 = 1 2 y 2 = – 5 – D 2 · 2 = – 5 – 7 4 = – 3

Следовательно, x 2 = 1 2 или x 2 = – 3 .

Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .

Ответ: x = ± 1 2 и x = ± i · 3 .

Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .

Решение

Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

16 y 2 + 145 y + 9 = 0 D = 145 2 – 4 · 16 · 9 = 20449 y 1 = – 145 + D 2 · 16 = – 145 + 143 32 = – 1 16 y 2 = – 145 – D 2 · 16 = – 145 – 143 32 = – 9

Поэтому, в силу замены переменной, x 2 = – 1 16 или x 2 = – 9 .

Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 – B y 2 + A C – 4 D y – A 2 D + 4 B D – C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 – B + y 0 x 2 + A 2 y 0 – C x + y 0 2 4 – D = 0 , у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Найти корни уравнения x 4 + 3 x 3 + 3 x 2 – x – 6 = 0 .

Решение

Имеем А = 3 , В = 3 , С = – 1 , D = – 6 . Применим метод Феррари для решения данного уравнения.

Составим и решим кубическое уравнение:
y 3 – B y 2 + A C – 4 D y – A 2 D + 4 B D – C 2 = 0 y 3 – 3 y 2 + 21 y – 19 = 0

Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 – 3 · 1 2 + 21 · 1 – 19 = 0 .

Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 – B + y 0 x 2 + A 2 y 0 – C x + y 0 2 4 – D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0

x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 – 1 2 x – 5 2 = 0

x 2 + 2 x + 3 = 0 или x 2 + x – 2 = 0

Корнями первого уравнения будут x = – 1 ± i · 2 , корнями второго х = 1 и х = – 2 .

Ответ: x 1 , 2 = – 1 ± i 2 , x 3 = 1 , x 4 = – 2 .

Уравнение четвертой степени

Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех значений неизвестного (неизвестных), при которых соблюдается верное равенство. Такие значения неизвестного (неизвестных) являются корнями или решением уравнения.

Уравнение вида ах 4 + bх 3 + сх 2 + dх + е = 0 называется уравнением 4-й степени с одним неизвестным. В результате решения уравнения получается 4 комплексных или вещественных корня.

Для решения приведенного уравнения 4-й степени вида: х 4 + Ах 3 + Вх 2 +Сх + D = 0 можно воспользоваться методом Феррари.

Составим кубическое уравнение: у 3 — Ву 2 + (АС — 4D)у — А 2 D + 4ВD — С 2 = 0.

Решаем полученное уравнение, находим один из его вещественных корней у₀, который используем для дальнейшего нахождения корней квадратных уравнений.
Получаем и решаем два квадратных уравнения: 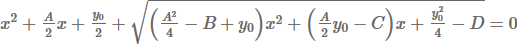. Корни уравнений будут корнями первоначального уравнения 4-й степени.

Если дано биквадратное уравнение 4-й степени вида: Ах 4 + Вх 2 + С = 0 и нужно найти его корни, можно свести его к квадратному, заменив переменную х 2 на у (у = х 2 ). В результате получим уравнение вида: Ау 2 + Ву + С = 0. Далее решаем квадратное уравнение через дискриминант.

Если дано возвратное уравнение 4-й степени вида: Ах 4 + Вх 3 + Сх 2 + Вх + А = 0 и нужно найти его корни, следует разделить уравнение на х 2 , получим:
Ах 2 + Вх + С + В / х + А / х 2 = 0.

Группируем и выносим коэффициенты за скобки: Ах 2 + А / х 2 + Вх + В / х + С = 0; А(х 2 + 1 / х 2 ) + В(х + 1 / х) + С = 0.

Произведем замену переменных: х + 1 / х = у; х 2 + 1 / х 2 = у 2 — 2, получим: А(у 2 — 2) + Ву + С = 0.

Сводим уравнение 4-й степени к квадратному уравнению и решаем его через дискриминант Ау 2 + Ву + С — 2А = 0.

Находим у₁ и у₂, после чего возвращаемся к замене и находим корни.

Быстро решить любое уравнение вы сможете с помощью представленного на сайте онлайн калькулятора.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-chetvertoj-stepeni/

[/spoiler]

Всем привет! 🖐🖐🖐

🎯 В этой статье мы разберемся как отличить и как решать уравнение 4 степени!
🎯 Задания из ЕГЭ, ОГЭ, ВПР, иногда из учебников

✅ Решения подробные, будет понятно 😎
✅ В конце задания для тренировки 💪
✅ В комментах отвечу на ваши вопросы 😊
✅ И без лишней воды ☔☔☔

Вот какие уравнения мы разберем сегодня:

📝 Как отличить и как решать уравнение 4 степени

Рассматриваем чем отличается уравнение 4 степени.

Способы решения:
◽ группировка и вынесение общего множителя
◽ деление столбиком многочлена на скобку (теорема Безу)
◽ формулы сокращенного умножения
◽ замена

Скрин:

📝 Уравнение 1

Как решить такие простые уравнения 4 степени? Избавляемся от 4 степени.

Скрины решения:

📝 Уравнение 2

Данное уравнение 4 степени является биквадратным. Делаем замену x²=t.

Скрины решения:

📝 Уравнение 3

Решаем:
◽ 1 способ – группировка и вынесение общего множителя за скобку
◽ 2 способ – деление столбиком многочлена на скобку

Скрины решения:

📝 Уравнение 4

Способы решения:
◽ 1 способ – группировка и вынесение общего множителя за скобку
◽ 2 способ – деление столбиком многочлена на скобку

Скрины решения:

📝 Уравнение 5

Решаем с помощью замены, сводим к квадратному уравнению.

Скрины решения:

📝 Уравнение 6

Решаем с помощью замены, в итоге сводим к квадратному уравнению.

Скрины решения:

А вот такую замену предложил сделать один мой зритель, очень удобно. Для замены на конце выражения выбирается +5, то есть число, которое находится посередине между +4 и +6. Этот способ замены дает возможность свернуть по формуле сокращенного умножения.

📝 Уравнение 7

Решаем это уравнение с учетом его особенности – в левой части стоит сумма квадратов.

Скрины решения:

📝 Уравнение 8

Способы решения:
◽ 1 способ – разложить на множители
◽ 2 способ – формула сокращенного умножения
◽ 3 способ – избавиться от квадратов

Скрины решения:

📝 Уравнение 9

Способы решения:
◽ 1 способ – формула сокращенного умножения
◽ 2 способ – понизить степень уравнения

Скрины решения:

📝 Уравнение 10

Сначала раскрываем скобки и после этого решаем как биквадратное.

Скрины решения:

📝 Задания для тренировки

Реши сам по аналогии и напиши свои ответы в комментариях! 😋😋😋

⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜⚜

✅ Оглавление:

👉 Как решать любое уравнение (цикл занятий) здесь

✍ Занятие 0 Виды уравнений здесь
✍ Занятие 1 Линейное уравнение здесь
✍ Занятие 2 Часть 1 Полные квадратные уравнения здесь
✍ Занятие 2 Часть 2 Неполные квадратные уравнения здесь
✍ Занятие 2 Часть 3 Квадратные уравнения со скобками здесь
✍ Занятие 3 Часть 1 Стандартные кубические уравнения здесь
✍ Занятие 3 Часть 2 Кубические уравнения со скобками здесь
✍ Занятие 4 Уравнение 4 степени здесь
✍ Занятие 5 Уравнение со скобками (вида Произведение = 0) здесь
✍ Занятие 6 Уравнение со скобками (вида Произведение = выр) здесь
✍ Занятие 7 Дробное уравнение (вида Дробь = 0) здесь
✍ Занятие 8 Дробное уравнение (вида Дробь = выражению) здесь
✍ Занятие 9 Иррациональное уравнение (с корнями) здесь
✍ Занятие 10 Уравнение с модулем здесь
✍ Занятие 11 Часть 1 Простые показательные уравнения здесь
✍ Занятие 11 Часть 2 Сложные показательные уравнения здесь
✍ Занятие 12 Часть 1 Простые логарифмические уравнения здесь
✍ Занятие 12 Часть 2 Сложные логарифмические уравнения здесь
✍ Занятие 13 Тригонометрическое уравнение здесь
✍ Занятие 14 Уравнение смешанного типа здесь

🧭 Путеводитель по каналу Подслушано по Математике

здесь

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).

Так как функция является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если , то функция возрастает до плюс бесконечности с обеих сторон, а значит, имеет глобальный минимум. Аналогично, если , то функция убывает до минус бесконечности с обеих сторон, а значит, имеет глобальный максимум.

Теорема Виета для уравнения четвёртой степени[править | править код]

Корни уравнения четвёртой степени связаны с коэффициентами следующим образом:

История[править | править код]

Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.

Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,^[1] а было опубликовано только в 1545 вместе с решением кубического уравнения наставника Феррари — Джероламо Кардано в книге «Великое искусство»^[2].

То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824.
Записки, оставленные Галуа,
позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.^[3]

Решения[править | править код]

Решение через резольвенту[править | править код]

Решение уравнения четвёртой степени

сводится к решению кубической резольвенты

Корни резольвенты связаны с корнями исходного уравнения (которые и нужно найти) следующими соотношениями:

Корни резольвенты могут быть найдены по формуле Кардано.
Три формулы соотношений между и вместе с уравнением (соотношение Виета для коэффициента при )

дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.

Решение Декарта — Эйлера[править | править код]

В уравнении четвёртой степени

сделаем подстановку , получим уравнение в следующем виде (оно называется «неполным»):

где

Корни такого уравнения равны одному из следующих выражений:

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

причём  — это корни кубического уравнения

Решение Феррари[править | править код]

Решение уравнения четвёртой степени вида может быть найдено по методу Феррари.
Если  — произвольный корень кубического уравнения

(2)

(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений

где подкоренное выражение в правой части является полным квадратом.

Биквадратное уравнение[править | править код]

Биквадратное уравнение^[4] — алгебраическое уравнение четвёртой степени вида , где  — заданные комплексные числа и . Иначе говоря, это уравнение четвёртой степени, у которого второй и четвёртый коэффициенты равны нулю. Подстановкой оно сводится к квадратному уравнению относительно .

Четыре его корня находятся по формуле

Возвратные уравнения четвёртой степени[править | править код]

Возвратное уравнение четвёртой степени является также относительно легко решаемым: для такого, что , решение находится приведением к виду:

,

После замены ищется решение квадратного уравнения , а затем — квадратного уравнения .

Примечания[править | править код]

Литература[править | править код]

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 2003. — 832 с. — 5000 экз. — ISBN 5-8114-0485-9.
• Лекция 4 в кн.: Табачников С. Л., Фукс Д. Б. Математический дивертисмент. — М.: МЦНМО, 2011. — 512 с. — 2000 экз. — ISBN 978-5-94057-731-7.

Ссылки[править | править код]

• Решение Феррари (англ.). Дата обращения: 27 сентября 2009. Архивировано 19 февраля 2012 года.
• Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Biquadratic Equation (англ.) на сайте Wolfram MathWorld.
• Biquadratic equation (англ.) на сайте PlanetMath.

Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.

В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, разложение на множители, группировка, использование симметрии, однородности, деление многочлена на многочлен. Они вполне могут встретиться на ЕГЭ и олимпиадах в уравнениях, неравенствах и задачах с параметрами.
Также мы рассматриваем применение свойств функций, метод оценки, выделение полного квадрата, графический способ.

Вспомним основные понятия.

Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.

Например, число 3 – корень уравнения 2x = 6.

Решить уравнение – значит найти его корни или доказать, что их нет.

Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.

Например, уравнения  и  равносильны. Их корни совпадают:  или 

В этой статье мы рассмотрим рациональные уравнения. В них переменная х входит в целой степени. Стандартный вид такого уравнения: слева многочлен, справа ноль.
Например, уравнение первой степени имеет вид , где По-другому оно называется линейным уравнением, и вы с ним хорошо знакомы.

Уравнение второй степени приводится к виду , где Это квадратное уравнение, и с ним тоже все просто.

Уравнение третьей степени имеет вид , где

В общем виде такие уравнения n-й степени можно записать так:
, где х — переменная, — некоторые числа, причём

Теорема. Уравнение n-й степени имеет не более n действительных корней.

Это значит, что у квадратного уравнения не более двух корней. У уравнения третьей степени не более трех корней.
Как же найти эти корни?

к оглавлению ▴

Метод замены переменной

Замена переменной – ключ к решению многих задач.

Самый простой пример – биквадратное уравнение.

Так называется уравнение вида . Оно решается с помощью замены , где

1. Решим уравнение .

Решение:

Сделаем замену , тогда

или

Значение переменной не удовлетворяет условию замены, так как

Значит,

Ответ:

2.Решим уравнение

Решение:

Пусть Это уравнение имеет два корня: или . Оба корня отрицательны и не удовлетворяют условию . Значит, исходное уравнение не имеет действительных корней.

Ответ:

Такой символ означает, что корней нет, множество корней исходного уравнения является пустым.

3. Решим уравнение:

Решение:

Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.

Сделаем замену  Тогда 

С новой переменной уравнение стало проще:

Умножим обе части на 10t. Получим квадратное уравнение:

Корни этого уравнения:  или 

Вернемся к переменной 

Если , то 

Отсюда 

Дискриминант этого уравнения отрицателен, корней нет.

Если , то  Получим квадратное уравнение для :

У этого уравнения два корня:  или  Это ответ.

4. Решим уравнение

Решение:
Мы видим, что выражение в уравнении встречается дважды. Хорошо бы обозначить его новой переменной, сделать замену.

Введем новую переменную

Уравнение примет вид: или

Возвращаемся к переменной х:

У нас появилось новое обозначение: – знак совокупности.
Такой знак означает «или».

Мы получили совокупность из двух квадратных уравнений.

Решим эти уравнения по очереди.

2) Уравнение не имеет корней. Его дискриминант отрицателен.

Ответ: 1; 0,25

5. Решим уравнение

Решение:

Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.

Посмотрим на уравнение внимательно.

На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки 

Сделаем замену , тогда .

Тогда:

Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:

И еще одна замена: .

Обычное квадратное уравнение. Замечательно!

Подберем его корни по теореме Виета. Заметим, что

;  отсюда  ,  .

Если , то нет решений.

Если , то Тогда или

Если , то .

Если , то .

Ответ: 4; –8.

Дальше – еще интереснее.

6. Решите уравнение

Решение:

Сделаем замену . То, что в правой части в скобках, заменили на новую переменную.

.

Получили квадратное уравнение:

Если , то

Если , то

Ответ:

к оглавлению ▴

Метод разложения на множители

Этот метод удобен, когда в правой части уравнения стоит ноль, а в левой – выражение, зависящее от переменной.

Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а остальные при этом не теряют смысла.

7. Решим уравнение .

Конечно, не нужно перемножать все «скобки». Левая часть уравнения равна нулю, если х=0 или х=2 или х=3 или х=5. Все эти значения переменной – корни уравнения.

Ответ: 0; 2; 3; 5.

8. Решим уравнение

Решение:

Вынесем за скобки ,то есть разложим левую часть на множители.

Ответ:

Мы записали корни уравнения в виде множества из двух значений переменной, -2 и 0. Это одна из возможных форм записи ответа.
Метод разложения на множители часто применяется вместе с методом группировки.

к оглавлению ▴

Метод группировки слагаемых

9. Решите уравнение

Решение:

Разложим левую часть уравнения на множители. Сгруппируем слагаемые:

Первые два слагаемых – сумма кубов. Применим формулу: . Получим:

.

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Записывается это так:

Ответ: -2; 1; 4.

Здесь мы тоже использовали знак совокупности.

Запись читается как « или или ».

Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.

10. Решите уравнение

Решение:

Разложим левую часть уравнения множители методом группировки.

Ответ:

11. Решите уравнение

Решение:

Сгруппируем слагаемые:

А если сделать замену ?

Тогда .

Получаем квадратное уравнение: . Удачная замена!

Если , то , нет решений.

Если , то

, .

Ответ: .

к оглавлению ▴

Подбор целого корня и деление многочлена на многочлен уголком

Рассмотрим еще один метод решения уравнений третьей, четвертой и более высоких степеней.

12. Решите уравнение

Решение:

Разложить левую часть на множители с первой попытки не удается.

Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.

Выпишем целые делители числа 24:

1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24

Подставляя их по очереди в уравнение, при получаем верное равенство:

Это значит, что левую часть уравнения можно разложить на множители:

, где .

Чтобы найти , поделим выражение на . В столбик. Так же, как мы делим друг на друга числа.

Немного непривычно, да? Потренируйтесь – у вас получится!

Ответ: 2; 3; 4.

13. Решите уравнение

Решение:

Разложить на множители? Но как? И замена не видна сразу. Посмотрим на уравнение внимательно. Его коэффициенты: 1, – 5, 4, – 5, 1.

Такое уравнение называется симметрическим, или возвратным.

Разделим обе его части на . Мы можем это сделать, поскольку не является корнем нашего уравнения.

Теперь группируем слагаемые:

Сделаем замену .

Тогда

Получили уравнение . Легко!

Ответ:

14. Решите уравнение

Решение:

Разделив обе части уравнения на , получим:

Группируем слагаемые:

Сделаем замену , тогда

Наше уравнение примет вид:

Обратная замена:

Ответ:

к оглавлению ▴

Однородные уравнения

В школьном курсе математики проходят однородные показательные и однородные тригонометрические уравнения. Однородные алгебраические уравнения решаются тем же методом: делением на старшую степень.

15. Решите уравнение

Решение:

Это однородное уравнение. Разделим каждое слагаемое на при условии .

Получим:

Выполним замену:

Получим уравнение:

Обратная замена приведет нас к совокупности квадратных уравнений:

Решим эти квадратные уравнения.

Мы сказали, что поделить обе части уравнения на можно, только если Проверим, что будет, если . Тогда . Такое значение переменной не является корнем уравнения.

Ответ:

Рассмотрим еще одно однородное уравнение.

16. Решите уравнение

Решение:

не является корнем уравнения, поэтому разделим уравнение на и получим

Замена приводит к квадратному уравнению:

Его корни и

Обратная замена дает совокупность квадратных уравнений:

Решив эти квадратные уравнения, получаем корни:

Ответ:

Покажем еще несколько методов решения алгебраических уравнений. Они встречаются также в задачах с параметрами.

к оглавлению ▴

Выделение полного квадрата

17. Решите уравнение

Решение:

В правой части уравнения сумма двух квадратов. Добавим и вычтем удвоенное произведение двух выражений:

Свернем полный квадрат по формуле сокращенного умножения.

Замена приведет уравнение к виду:

или

Обратная замена дает совокупность двух квадратных уравнений:

Корни первого из этих уравнений:

Второе уравнение не имеет корней, его дискриминант отрицателен.

Ответ:

к оглавлению ▴

Метод оценки

18. Решим уравнение

Решение:

Преобразуем правую часть уравнения:

Уравнение примет вид:

Оценим левую и правую части уравнения.

Так как то равенство выполняется, только если и левая, и правая его части равны нулю.

Уравнение равносильно системе:

;

Система решений не имеет.

Ответ: корней нет.

При решении мы пользовались следующей теоремой:
Теорема. Если в уравнении функция ограничена сверху и , а функция ограничена снизу, причем , то уравнение равносильно системе:

Если система решений не имеет, то у данного уравнения корней нет.

Читайте о том, как метод оценки применяется в задачах с параметрами.

к оглавлению ▴

Использование свойств функций

Еще один нетривиальный метод решения уравнений – подобрать корень и доказать, что других корней нет.

Здесь нам поможет следующая теорема:
Теорема. Если в уравнении функция является монотонно возрастающей, а функция монотонно убывающей или постоянной, то уравнение не может иметь более одного корня.

19. Решите уравнение

Решение:

Левая часть уравнения представляет собой функцию, монотонно возрастающую при любом значении переменной х, т.к. является суммой монотонно возрастающих функций, а правая часть постоянна. Поэтому, если уравнения имеет корень, то он единственный.

Подбором находим, что т.к.

Ответ: -1.

20. Решите уравнение

Решение:

Функция является возрастающей (как сумма двух возрастающих функций), а правая часть постоянна. Уравнение имеет не более одного корня. Подбором находим, что — корень, так как

Других корней быть не может.
Ответ: 1.

к оглавлению ▴

Графический метод решения уравнений

Чтобы решить графически уравнение , строим в одной системе координат графики функций и и находим точки пересечения этих графиков. Абсциссы точек пересечения графиков — это корни уравнения .

21. Решите графически уравнение

Решение:

Запишем уравнение в виде . Построим в одной системе координат графики функций и

Графики функций пересекаются в единственной точке — корень уравнения, поскольку Других корней нет.
Ответ: 2.

Список литературы:

1. О. Ю. Черкасов, А. Г. Якушев. Домашний репетитор. Математика. Интенсивный курс подготовки к экзамену.

2. А. Г. Мордкович. Решаем уравнения.