Как найти дискриминант в пайтоне

Перейти к содержанию

from math import sqrt

a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))

from math import sqrt

a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))

d = b**2 - 4 * a * c

x1, x2 = frac{-bpmsqrt{D}}{2a}

from math import sqrt

a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))

d = b**2 - 4 * a * c

if d > 0:
    x1 = (-b + sqrt(d) / (2 * a))
    x2 = (-b - sqrt(d) / (2 * a))
    print(f'x1 = {x1:.2f}; x2 = {x2:.2f}')

from math import sqrt

a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))

d = b**2 - 4 * a * c

if d > 0:
    x1 = (-b + sqrt(d) / (2 * a))
    x2 = (-b - sqrt(d) / (2 * a))
    print(f'x1 = {x1:.2f}; x2 = {x2:.2f}')
elif d == 0:
    x1 = -b / (2 * a)
    print(f'x1 = {x1:.2f}')

from math import sqrt

a = float(input('a = '))
b = float(input('b = '))
c = float(input('c = '))

d = b**2 - 4 * a * c

if d > 0:
    x1 = (-b + sqrt(d) / (2 * a))
    x2 = (-b - sqrt(d) / (2 * a))
    print(f'x1 = {x1:.2f}; x2 = {x2:.2f}')
elif d == 0:
    x1 = -b / (2 * a)
    print(f'x1 = {x1:.2f}')
else:
    print('Нет корней')

Квадратные уравнения являются одним из наиболее распространенных типов уравнений, которые встречаются в математике и науке. Решение квадратных уравнений на Python может быть полезно в различных областях, таких как научные исследования, инженерные расчеты, финансовая аналитика и многих других.

В данной статье мы рассмотрим несколько примеров решения квадратных уравнений на Python с подробными объяснениями.

Решение квадратного уравнения с использованием дискриминанта на Python

main.py

from math import sqrt

def solve_quadratic_equation(a, b, c):
    """
    Решает квадратное уравнение ax^2 + bx + c = 0

    :param a: коэффициент при x^2
    :param b: коэффициент при x
    :param c: свободный член
    :return: корни уравнения
    """
    discriminant = b**2 - 4*a*c
    if discriminant > 0:
        x1 = (-b + sqrt(discriminant)) / (2*a)
        x2 = (-b - sqrt(discriminant)) / (2*a)
        return x1, x2
    elif discriminant == 0:
        x1 = -b / (2*a)
        return x1
    else:
        return None

# Задаем коэффициенты уравнения
a = 1
b = -3
c = 2

# Решение уравнения и вывод результатов
result = solve_quadratic_equation(a, b, c)
if result is None:
    print("Уравнение не имеет действительных корней")
elif isinstance(result, tuple):
    print(f"Корни уравнения: x1 = {result[0]}, x2 = {result[1]}")
else:
    print(f"Корень уравнения: x = {result}")
    
# Корни уравнения: x1 = 2.0, x2 = 1.0

Данный код представляет функцию solve_quadratic_equation, которая решает квадратное уравнение вида ax^2 + bx + c = 0, где a, b и c – коэффициенты уравнения. Функция использует импортированную из модуля math функцию sqrt для вычисления квадратного корня.

Функция solve_quadratic_equation принимает три аргумента – коэффициенты a, b и c уравнения, и возвращает корни уравнения в виде кортежа (tuple) или одиночного значения, в зависимости от количества корней.

Решение системы квадратных уравнений в Python

main.py

import math

def solve_quadratic_equation(a, b, c):
    """
    Решает квадратное уравнение ax^2 + bx + c = 0

    :param a: коэффициент при x^2
    :param b: коэффициент при x
    :param c: свободный член
    :return: корни уравнения
    """
    discriminant = b**2 - 4*a*c
    if discriminant > 0:
        x1 = (-b + math.sqrt(discriminant)) / (2*a)
        x2 = (-b - math.sqrt(discriminant)) / (2*a)
        return x1, x2
    elif discriminant == 0:
        x1 = -b / (2*a)
        return x1
    else:
        return None

def solve_system_of_equations(eq1, eq2):
    """
    Решает систему из двух квадратных уравнений

    :param eq1: кортеж с коэффициентами первого уравнения (a, b, c)
    :param eq2: кортеж с коэффициентами второго уравнения (a, b, c)
    :return: корни системы уравнений
    """
    a1, b1, c1 = eq1
    a2, b2, c2 = eq2

    # Решение первого уравнения
    x1 = solve_quadratic_equation(a1, b1, c1)
    if x1 is None:
        return None

    # Решение второго уравнения
    x2 = solve_quadratic_equation(a2, b2, c2)
    if x2 is None:
        return None

    return x1, x2

# Задаем систему уравнений
eq1 = (1, -3, 2)
eq2 = (2, 5, -3)

# Решение системы уравнений и вывод результатов
result = solve_system_of_equations(eq1, eq2)
if result is None:
    print("Система уравнений не имеет действительных корней")
else:
    x1, x2 = result
    print(f"Корни системы уравнений: x1 = {x1}, x2 = {x2}")
    
# Корни системы уравнений: x1 = (2.0, 1.0), x2 = (0.5, -3.0)

Данный код решает систему из двух квадратных уравнений и выводит результаты.

Функция solve_quadratic_equation(a, b, c) решает квадратное уравнение вида ax^2 + bx + c = 0, где a, b и c – это коэффициенты уравнения. Она использует дискриминант (discriminant), который вычисляется как разность квадрата коэффициента при x (b) и произведения {"4 * a * c"}. Затем, в зависимости от значения дискриминанта, функция возвращает корни уравнения или None, если уравнение не имеет действительных корней.

Решение квадратного уравнения с использованием библиотеки numpy для работы с массивами и матрицами

main.py

import numpy as np

def solve_quadratic_equation(a, b, c):
    """
    Решает квадратное уравнение ax^2 + bx + c = 0

    :param a: коэффициент при x^2
    :param b: коэффициент при x
    :param c: свободный член
    :return: корни уравнения
    """
    discriminant = b**2 - 4*a*c
    if discriminant > 0:
        x1 = (-b + np.sqrt(discriminant)) / (2*a)
        x2 = (-b - np.sqrt(discriminant)) / (2*a)
        return x1, x2
    elif discriminant == 0:
        x1 = -b / (2*a)
        return x1
    else:
        return None

# Задаем коэффициенты уравнения
a = 1
b = -3
c = 2

# Решение уравнения и вывод результатов
result = solve_quadratic_equation(a, b, c)
if result is None:
    print("Уравнение не имеет действительных корней")
elif isinstance(result, tuple):
    print(f"Корни уравнения: x1 = {result[0]}, x2 = {result[1]}")
else:
    print(f"Корень уравнения: x = {result}")
    
# Корни уравнения: x1 = 2.0, x2 = 1.0

Данный код представляет функцию solve_quadratic_equation(a, b, c), которая решает квадратное уравнение вида ax^2 + bx + c = 0, где a, b и c – это коэффициенты уравнения, передаваемые в качестве аргументов в функцию.
Функция использует библиотеку NumPy, импортированную как np, для выполнения математических операций, таких как извлечение квадратного корня.

Заключение

Решение квадратных уравнений на Python может быть полезным навыком при работе с математическими и научными расчетами.

В данной статье мы рассмотрели три примера решения квадратных уравнений на Python.

Квадратное уравнение

Программа, позволяющая находить корни квадратного уравнения, – это один из примеров простых программ, которые можно написать на Python 3. Она хорошо подойдет для начинающих изучать этот язык программирования.

Постановка задачи

Уравнение, которое будем решать, выглядит следующим образом: a·x²+b·x+c=0. Пользователю предлагается ввести значения a, b и с в терминале. После этого программа посчитает дискриминант. На его основе найдем решения уравнения – значения x, для которых будет выполняться равенство.

Вот пример работы программы, которая будет написана.

Программа

Для решения квадратных уравнений на Python 3 напишем код, приведенный ниже. Разберем некоторые моменты, которые мы использовали в этой простой программе:

• print — эта функция выводит на экран информацию.
• input — выводит информацию и предлагает пользователю ввести данные.
• b**2 — это возведение в степень, в данном случае переменная b возводится в квадрат.
• str — эта функция приводит данные к строковому виду.
• if-elif-else — это условные операторы в языке Python. Исходя из значения discriminant мы определяем количество корней квадратного уравнения.
• discriminant ** 0.5 — с помощью такого способа извлекаем квадратный корень. В Python есть несколько способов извлечения корней, например, с помощью функции sqrt из библиотеки math. Про способы извлечения корней в Python описано в отдельной статье.

Запустим программу и введём нужные коэффициенты.

Все посчитано, найдены два корня, которые будут являться решением квадратного уравнения.

Дополнительно

Хотелось бы уделить внимание ещё одному моменту. Если дискриминант отрицательный, то действительных корней нет. Но будут комплексные корни. Если мы хотим их обрабатывать, то следует изменить конструкцию условных операторов следующим образом:

Тогда пример решения уравнения будет выглядеть следующим образом:

Как видим, получили два комплексных корня.

Этот простой код написанный на Python 3 можно для обучения программированию немного усложнить:

• Предлагать запрос в конце программы «Решить ещё одно уравнение (y/n): ». И если пользователь введет «y», то заново запросить коэффициенты. Это нужно делать в цикле. Подробнее о циклах в Python можно прочитать здесь.
• Сделать проверку корректности ввода. Ведь пользователь вместо числа может ввести какую-нибудь строку, которая не будет корректно обработана. Про проверку на число описано в отдельной статье.

Библиотека Sympy: символьные вычисления в Python

Что такое SymPy ? Это библиотека символьной математики языка Python. Она является реальной альтернативой таким математическим пакетам как Mathematica или Maple и обладает очень простым и легко расширяемым кодом. SymPy написана исключительно на языке Python и не требует никаких сторонних библиотек.

Документацию и исходный код этой библиотеки можно найти на ее официальной странице.

Первые шаги с SymPy

Используем SymPy как обычный калькулятор

В библиотеке SymPy есть три встроенных численных типа данных: Real , Rational и Integer . С Real и Integer все понятно, а класс Rational представляет рациональное число как пару чисел: числитель и знаменатель рациональной дроби. Таким образом, Rational(1, 2) представляет собой 1/2 , а, например, Rational(5, 2) — соответственно 5/2 .

Библиотека SymPy использует библиотеку mpmath , что позволяет производить вычисления с произвольной точностью. Таким образом, ряд констант (например, пи, e), которые в данной библиотеке рассматриваются как символы, могут быть вычислены с любой точностью.

Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.

В SymPy есть также класс, представляющий такое понятие в математике, как бесконечность. Он обозначается следующим образом: oo .

Символы

В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:

После их задания, с ними можно производить различные манипуляции.

С символами можно производить преобразования с использованием некоторых операторов языка Python. А именно, арифметических ( + , -` , “* , ** ) и логических ( & , | ,

Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:

Алгебраические преобразования

SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.

Раскрытие скобок

Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:

При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.

Упрощение выражений

Если вы хотите привести выражение к более простому виду (возможно, сократить какие-то члены), то используйте функцию simplify .

Также надо сказать, что для определенных видов математических функций существуют альтернативные, более конкретные функции для упрощения выражений. Так, для упрощения степенных функций есть функция powsimp , для тригонометрических — trigsimp , а для логарифмических — logcombine , radsimp .

Вычисления

Вычисления пределов

Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно limit(function, variable, point) . Например, если вы хотите вычислить предел функции f(x) , где x -> 0 , то надо написать limit(f(x), x, 0) .

Также можно вычислять пределы, которые стремятся к бесконечности.

Дифференцирование

Для дифференцирования выражений в SymPy есть функция diff(func, var) . Ниже даны примеры ее работы.

Проверим результат последней функции при помощи определения производной через предел.

tan 2 (?)+1 Результат тот же.

Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: diff(func, var, n) . Ниже приведено несколько примеров.

Разложение в ряд

Для разложения выражения в ряд Тейлора используется следующий синтаксис: series(expr, var) .

Интегрирование

В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции integrate() . Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:

Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:

Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.

Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).

Решение уравнений

При помощи SymPy можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция solveset() .

Как можно заметить, первое выражение функции solveset() приравнивается к 0 и решается относительно х . Также возможно решать некоторые уравнения с трансцендентными функциями.

Системы линейных уравнений

SymPy способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции solve() , которая используется для таких задач.

Факторизация

Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в SymPy предусмотрена функция factor() , которая способна производить факторизацию очень широкого класса полиномов.

Булевы уравнения

Также в SymPy реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция satisfiable() .

Данный результат говорит нам о том, что выражение (x & y) будет истинным тогда и только тогда, когда x и y истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат False .

Линейная алгебра

Матрицы

Матрицы в SymPy создаются как экземпляры класса Matrix :

В отличие от NumPy , мы можем использовать в матрицах символьные переменные:

И производить с ними разные манипуляции:

Дифференциальные уравнения

При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция dsolve() . Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр cls=Function в функцию symbols() .

Теперь f и g заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав f(x) .

Теперь решим следующее дифференциальное уравнение:

Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент hint=’separable’ .

Английский для программистов

Наш телеграм канал с тестами по английскому языку для программистов. Английский это часть карьеры программиста. Поэтому полезно заняться им уже сейчас

Математическая библиотека Python SymPy

SymPy — это библиотека Python для выполнения символьных вычислений. Это система компьютерной алгебры, которая может выступать как отдельное приложение, так и в качестве библиотеки для других приложений. Поработать с ней онлайн можно на https://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать даже в интерактивном режиме.

В SymPy есть разные функции, которые применяются в сфере символьных вычислений, математического анализа, алгебры, дискретной математики, квантовой физики и так далее. SymPy может представлять результат в разных форматах: LaTeX, MathML и так далее. Распространяется библиотека по лицензии New BSD. Первыми эту библиотеку выпустили разработчики Ondřej Čertík и Aaron Meurer в 2007 году. Текущая актуальная версия библиотеки — 1.6.2.

Вот где применяется SymPy:

• Многочлены
• Математический анализ
• Дискретная математика
• Матрицы
• Геометрия
• Построение графиков
• Физика
• Статистика
• Комбинаторика

Установка SymPy

Для работы SymPy требуется одна важная библиотека под названием mpmath . Она используется для вещественной и комплексной арифметики с числами с плавающей точкой произвольной точности. Однако pip установит ее автоматически при загрузке самой SymPy:

Такие дистрибутивы, как Anaconda, Enthough, Canopy и другие, заранее включают SymPy. Чтобы убедиться в этом, достаточно ввести в интерактивном режиме команду:

Исходный код можно найти на GitHub.

Символьные вычисления в SymPy

Символьные вычисления — это разработка алгоритмов для управления математическими выражениями и другими объектами. Такие вычисления объединяют математику и компьютерные науки для решения математических выражений с помощью математических символов.

Система компьютерной алгебры же, такая как SymPy, оценивает алгебраические выражения с помощью тех же символов, которые используются в традиционных ручных методах. Например, квадратный корень числа с помощью модуля math в Python вычисляется вот так:

Как можно увидеть, квадратный корень числа 7 вычисляется приблизительно. Но в SymPy квадратные корни чисел, которые не являются идеальными квадратами, просто не вычисляются:

Вот каким будет вывод этого кода: sqrt(7) .

Это можно упростить и показать результат выражения символически таким вот образом:

В случае с модулем math вернется число, а вот в SymPy — формула.

Для рендеринга математических символов в формате LaTeX код SymPy, используйте Jupyter notebook:

Если выполнить эту команду в IDLE, то получится следующий результат:

Квадратный корень неидеального корня также может быть представлен в формате LaTeX с помощью привычных символов:

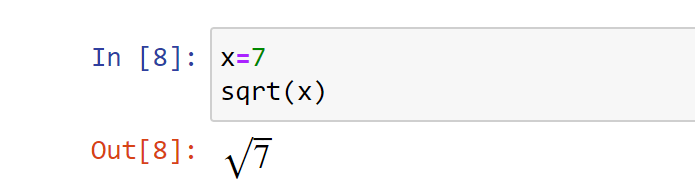
Символьные вычисления с помощью таких систем, как SymPy, помогают выполнять вычисления самого разного рода (производные, интегралы, пределы, решение уравнений, работа с матрицами) в символьном виде.

В пакете SymPy есть разные модули, которые помогают строить графики, выводить результат (LaTeX), заниматься физикой, статистикой, комбинаторикой, числовой теорией, геометрией, логикой и так далее.

Числа

Основной модуль в SymPy включает класс Number , представляющий атомарные числа. У него есть пара подклассов: Float и Rational . В Rational также входит Integer .

Класс Float

Float представляет числа с плавающей точкой произвольной точности:

SymPy может конвертировать целое число или строку в число с плавающей точкой:

При конвертации к числу с плавающей точкой, также можно указать количество цифр для точности:

Представить число дробью можно с помощью объекта класса Rational , где знаменатель — не 0:

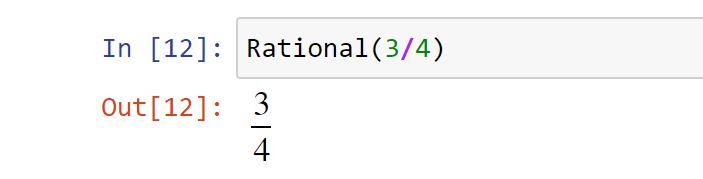
Если число с плавающей точкой передать в конструктор Rational() , то он вернет дробь:

Для упрощения можно указать ограничение знаменателя:

Выведется дробь 1/5 вместо 3602879701896397/18014398509481984.

Если же в конструктор передать строку, то вернется рациональное число произвольной точности:

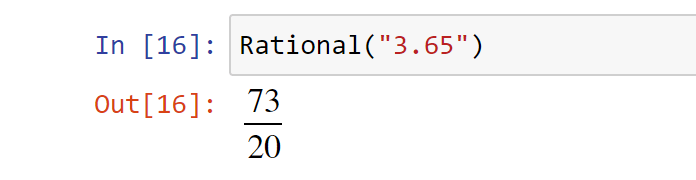
Также рациональное число можно получить, если в качестве аргументов передать два числа. Числитель и знаменатель доступны в виде свойств:

Класс Integer

Класс Integer в SymPy представляет целое число любого размера. Конструктор принимает рациональные и числа с плавающей точкой. В результате он откидывает дробную часть:

Также есть класс RealNumber , который является алиасом для Float . В SymPy есть классы-одиночки Zero и One , доступные через S.Zero и S.One соответственно.

Другие числовые объекты-одиночки — Half , NaN , Infinity и ImaginaryUnit .

Бесконечность представлена в виде объекта-символа oo или как S.Infinity :

ImaginaryUnit можно импортировать как символ I , а получить к нему доступ — через S.ImaginaryUnit .

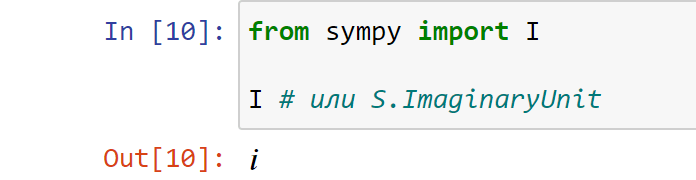
Символы

Symbol — самый важный класс в библиотеке SymPy. Как уже упоминалось ранее, символьные вычисления выполняются с помощью символов. И переменные SymPy являются объектами класса Symbol .

Аргумент функции Symbol() — это строка, содержащая символ, который можно присвоить переменной.

Код выше является эквивалентом этого выражения:

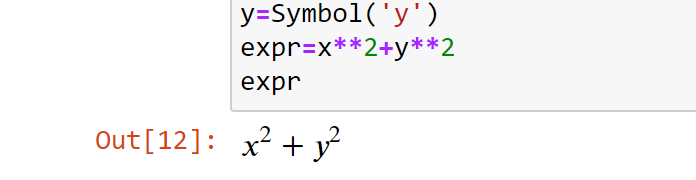
Символ может включать больше одной буквы:

Также в SymPy есть функция Symbols() , с помощью которой можно определить несколько символов за раз. Строка содержит названия переменных, разделенные запятыми или пробелами.

В модуле abc можно найти элементы латинского и греческого алфавитов в виде символов. Таким образом вместо создания экземпляра Symbol можно использовать метод:

Однако C, O, S, I, N, E и Q являются заранее определенными символами. Также символы с более чем одной буквы не определены в abc. Для них нужно использовать объект Symbol . Модуль abs определяет специальные имена, которые могут обнаружить определения в пространстве имен SymPy по умолчанию. сlash1 содержит однобуквенные символы, а clash2 — целые слова.

Индексированные символы (последовательность слов с цифрами) можно определить с помощью синтаксиса, напоминающего функцию range() . Диапазоны обозначаются двоеточием. Тип диапазона определяется символом справа от двоеточия. Если это цифра, то все смежные цифры слева воспринимаются как неотрицательное начальное значение.

Смежные цифры справа берутся на 1 больше конечного значения.

Подстановка параметров

Одна из базовых операций в математических выражениях — подстановка. Функция subs() заменяет все случаи первого параметра на второй.

Этот код даст вывод, эквивалентный такому выражению.

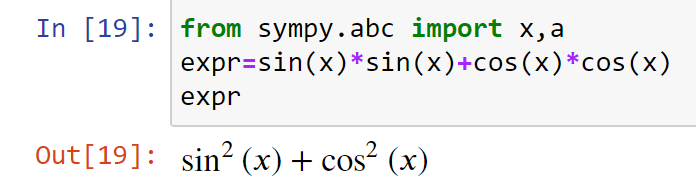
А кодом expr.subs(x,a) мы получим туже формулу, но с a вместо x .

Эта функция полезна, когда требуется вычислить определенное выражение. Например, нужно посчитать значения выражения, заменив a на 5 :

Также функция используется для замены подвыражения другим подвыражением. В следующем примере b заменяется на a+b .

Это дает такой вывод:

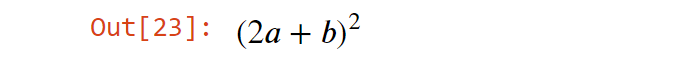
Функция simplify()

Функция simplify() используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целые числа, конвертируются в SymPy.Integer и так далее. Строки также конвертируются в выражения SymPy:

Любой объект Python можно конвертировать в объект SymPy. Однако учитывая то, что при преобразовании используется функция eval() , не стоит использовать некорректные выражения, иначе возникнет ошибка SimplifyError .

Функция simplify() принимает следующий аргумент: strict=False . Если установить True , то преобразованы будут только те типы, для которых определено явное преобразование. В противном случае также возникнет ошибка SimplifyError . Если же поставить False , то арифметические выражения и операторы будут конвертированы в их эквиваленты SumPy без вычисления выражения.

Функция evalf()

Функция вычисляет данное числовое выражение с точностью до 100 цифр после плавающей точки. Она также принимает параметр subs , как объект словаря с числовыми значениями для символов. Например такое выражение:

Даст такой результат: ?? 2

Вычислим выражение с помощью evalf() и заменим r на 5:

По умолчанию точность после плавающей точки — 15, но это значение можно перезаписать до 100. Следующее выражение вычисляет, используя вплоть до 20 цифр точности:

Функция lambdify()

Функция lambdify() переводит выражения SymPy в функции Python. Если выражение, которое нужно вычислить, затрагивает диапазон значений, то функция evalf() становится неэффективной. Функция lambdify действует как лямбда-функция с тем исключением, что она конвертирует SymPy в имена данной числовой библиотеки, обычно NumPy. По умолчанию же она реализована на основе стандартной библиотеки math.

У выражения может быть больше одной переменной. В таком случае первым аргументом функции является список переменных, а после него — само выражение:

Но чтобы использовать numpy в качестве основной библиотеки, ее нужно передать в качестве аргумента функции lambdify() .

В этой функции использовались два массива numpy: a и b . В случае с ними выполнение гораздо быстрее:

Логические выражения

Булевы функции расположены в модуле sympy.basic.booleanarg . Их можно создать и с помощью стандартных операторов Python: & (And), | (Or),

(Not), а также >> и . Булевы выражения наследуются от класса Basic .

BooleanTrue.
Эта функция является эквивалентом True из Python. Она возвращает объект-одиночку, доступ к которому можно получить и с помощью S.true .

BooleanFalse.
А эта функция является эквивалентом False . Ее можно достать с помощью S.False .

And.
Функция логического AND оценивает два аргумента и возвращает False , если хотя бы один из них является False . Эта функция заменяет оператор & .

Or.
Оценивает два выражения и возвращает True , если хотя бы одно из них является True . Это же поведение можно получить с помощью оператора | .

Not.
Результат этой функции — отрицание булево аргумента. True, если аргумент является False , и False в противном случае. В Python за это отвечает оператор

Xor.
Логический XOR (исключающий OR) возвращает True, если нечетное количество аргументов равняется True , а остальные — False . False же вернется в том случае, если четное количество аргументов True , а остальные — False . То же поведение работает в случае оператора ^ .

В предыдущем примере один(нечетное число) аргумент является True , поэтому Xor вернет True . Если же количество истинных аргументов будет четным, результатом будет False , как показано дальше.

Nand.
Выполняет логическую операцию NAND. Оценивает аргументы и возвращает True , если хотя бы один из них равен False , и False — если они истинные.

Nor.
Выполняет логическую операцию NOR. Оценивает аргументы и возвращает False , если один из них True , или же True , если все — False .

Хотя SymPy и предлагает операторы ^ для Xor ,

для Not , | для Or и & для And ради удобства, в Python они используются в качестве побитовых. Поэтому если операнды будут целыми числами, результаты будут отличаться.

Equivalent.
Эта функция возвращает отношение эквивалентности. Equivalent(A, B) будет равно True тогда и только тогда, когда A и B оба будут True или False . Функция вернет True , если все аргументы являются логически эквивалентными. В противном случае — False .

Запросы

Модуль assumptions в SymPy включает инструменты для получения информации о выражениях. Для этого используется функция ask() .

Следующие свойства предоставляют полезную информацию о выражении:

algebraic(x)
Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 — это решение x2 − 2 = 0. Следовательно, это выражения является алгебраическим.

complex(x)
Предикат комплексного числа. Является истиной тогда и только тогда, когда x принадлежит множеству комплексных чисел.

composite(x)
Предикат составного числа, возвращаемый ask(Q.composite(x)) является истиной тогда и только тогда, когда x — это положительное число, имеющее как минимум один положительный делитель, кроме 1 и самого числа.

even, odd
ask() возвращает True , если x находится в множестве четных и нечетных чисел соответственно.

imaginary
Свойство представляет предикат мнимого числа. Является истиной, если x можно записать как действительное число, умноженное на мнимую единицу.

integer
Это свойство, возвращаемое Q.integer(x) , будет истинным только в том случае, если x принадлежит множеству четных чисел.

rational, irrational
Q.irrational(x) истинно тогда и только тогда, когда x — это любое реальное число, которое нельзя представить как отношение целых чисел. Например, pi — это иррациональное число.

positive, negative
Предикаты для проверки того, является ли число положительным или отрицательным.

zero, nonzero
Предикат для проверки того, является ли число нулем или нет.

[spoiler title=”источники:”]

http://pythonru.com/biblioteki/sympy-v-python

[/spoiler]