Как найти дискриминанты матриц - Сайт, где вы сможете решить свои вопросы

Определи́тель (детермина́нт) в линейной алгебре — скалярная величина, которая характеризует ориентированное «растяжение» или «сжатие» многомерного евклидова пространства после преобразования матрицей; имеет смысл только для квадратных матриц. Стандартные обозначения определителя матрицы — , |A| , ^[1].

Определитель квадратной матрицы размеров , заданной над коммутативным кольцом , является элементом кольца . Эта величина определяет многие свойства матрицы , в частности, матрица обратима тогда и только тогда, когда её определитель является обратимым элементом кольца . В случае, когда — поле, определитель матрицы равен нулю тогда и только тогда, когда ранг матрицы меньше , то есть когда системы строк и столбцов матрицы являются линейно зависимыми.

История[править | править код]

Теория определителей возникла в связи с задачей решения систем линейных уравнений.

К понятию определителя близко подошли авторы древнекитайского учебника «Математика в девяти книгах»^[2].

В Европе определители матриц 2 × 2 встречаются у Кардано в XVI веке.
Для старших размерностей определение детерминанта дано Лейбницем в 1693 году.
Первая публикация принадлежит Крамеру. Теория определителей создана Вандермондом, Лапласом, Коши и Якоби. Термин «определитель» в современном его значении ввёл О. Коши (1815), хотя ранее (1801) «детерминантом» К. Гаусс назвал дискриминант квадратичной формы.

Японский математик Сэки Такакадзу ввёл определители независимо в 1683 году^[3].

Определения[править | править код]

Через перестановки[править | править код]

Для квадратной матрицы $A=(a_{ij})$ размера её определитель вычисляется по формуле:

${displaystyle det A=sum _{alpha _{1},alpha _{2},ldots ,alpha _{n}}(-1)^{N(alpha _{1},alpha _{2},ldots ,alpha _{n})}cdot a_{1alpha _{1}}a_{2alpha _{2}}dots a_{nalpha _{n}}}$

где суммирование проводится по всем перестановкам ${displaystyle alpha _{1},alpha _{2},ldots ,alpha _{n}}$ чисел , а ${displaystyle N(alpha _{1},alpha _{2},ldots ,alpha _{n})}$ обозначает число инверсий в перестановке ${displaystyle alpha _{1},alpha _{2},ldots ,alpha _{n}}$ .

Таким образом, в определитель входит слагаемых, которые также называют «членами определителя».

Эквивалентная формула:

${displaystyle det A=sum _{i_{1},i_{2},ldots ,i_{n}=1}^{n}varepsilon _{i_{1}i_{2}dots i_{n}}cdot a_{1i_{1}}a_{2i_{2}}dots a_{ni_{n}}}$

где коэффициент ${displaystyle varepsilon _{i_{1}i_{2}dots i_{n}}}$ — символ Леви-Чивиты — равен:

0, если не все индексы ${displaystyle i_{1},i_{2},ldots ,i_{n}}$

различны,

1, если все индексы ${displaystyle i_{1},i_{2},ldots ,i_{n}}$

различны и подстановка ${displaystyle {begin{pmatrix}1&2&dots &n\i_{1}&i_{2}&dots &i_{n}end{pmatrix}}in S_{n}}$

чётна,

−1, если все индексы ${displaystyle i_{1},i_{2},ldots ,i_{n}}$

различны и подстановка ${displaystyle {begin{pmatrix}1&2&dots &n\i_{1}&i_{2}&dots &i_{n}end{pmatrix}}in S_{n}}$

нечётна.

Аксиоматическое построение (определение на основе свойств)[править | править код]

Понятие определителя может быть введено на основе его свойств. А именно, определителем вещественной матрицы называется функция $det :mathbb {R} ^{ntimes n}rightarrow mathbb {R}$ , обладающая следующими тремя свойствами^[4]:

— кососимметрическая функция строк (столбцов) матрицы .
— полилинейная функция строк (столбцов) матрицы .
, где — единичная -матрица.

Значение определителя матрицы[править | править код]

Для матрицы первого порядка значение детерминанта равно единственному элементу этой матрицы:

$Delta ={begin{vmatrix}a_{11}end{vmatrix}}=a_{11}$

Матрицы 2 x 2[править | править код]

Схема расчета определителя матрицы 2×2.

Площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма.

Для матрицы определитель вычисляется как:

$Delta ={begin{vmatrix}a&c\b&dend{vmatrix}}=ad-bc$

Эта матрица A может быть рассмотрена как матрица линейного отображения, преобразующего единичный квадрат в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d).

Абсолютное значение определителя |ad-bc| равно площади этого параллелограмма, и, таким образом, отражает коэффициент, на который масштабируются площади при преобразовании A.

Значение определителя со знаком (ориентированная площадь параллелограмма) помимо коэффициента масштабирования также показывает, выполняет ли преобразование A отражение.

Матрицы 3 x 3[править | править код]

Определитель матрицы можно вычислить по формуле:

$Delta ={begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}}=a_{11}{begin{vmatrix}a_{22}&a_{23}\a_{32}&a_{33}end{vmatrix}}-a_{12}{begin{vmatrix}a_{21}&a_{23}\a_{31}&a_{33}end{vmatrix}}+a_{13}{begin{vmatrix}a_{21}&a_{22}\a_{31}&a_{32}end{vmatrix}}=$

$=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}$

Для более удобного вычисления определителя третьего порядка можно воспользоваться правилом Саррюса или правилом треугольника.

Определитель матрицы, составленной из векторов равен их смешанному произведению в правой декартовой системе координат и, аналогично двумерному случаю, представляет собой ориентированный объём параллелепипеда, натянутого на . Геометрически определитель матрицы 3х3 означает объем параллелепипеда, построенного на векторах матрицы. ^[5]

Матрицы N × N[править | править код]

В общем случае, для матриц более высоких порядков (выше 2-го порядка) определитель можно вычислить, применив следующую рекурсивную формулу:

$Delta =sum _{j=1}^{n}(-1)^{1+j}a_{1j}{bar {M}}_{j}^{1}$

, где ${bar {M}}_{j}^{1}$

— дополнительный минор к элементу $a_{1j}$

. Эта формула называется разложением по строке.

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

$Delta =sum _{i=1}^{n}(-1)^{i+1}a_{i1}{bar {M}}_{1}^{i}$

Также справедливо и аналогичное разложение по любой строке (столбцу):

$Delta =sum _{j=1}^{n}(-1)^{i+j}a_{ij}{bar {M}}_{j}^{i}$

Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым строкам (столбцам):

${displaystyle Delta =sum _{1leqslant j_{1}<ldots <j_{k}leqslant n}(-1)^{i_{1}+ldots +i_{k}+j_{1}+ldots +j_{k}}M_{j_{1}ldots j_{k}}^{i_{1}ldots i_{k}}{bar {M}}_{j_{1}ldots j_{k}}^{i_{1}ldots i_{k}}}$

Альтернативные методы вычисления[править | править код]

Метод конденсации Доджсона, основанный на рекурсивной формуле:

${displaystyle Delta ={frac {{bar {M}}_{1}^{1}{bar {M}}_{k}^{k}-{bar {M}}_{1}^{k}{bar {M}}_{k}^{1}}{{bar {M}}_{1,k}^{1,k}}}}$

Основные свойства определителей[править | править код]

Следующие свойства отражают основные результаты теории определителей, применение которых выходит далеко за пределы этой теории:

(Определитель единичной матрицы равен 1);
${displaystyle det cA=c^{n}det A}$ (Определитель является однородной функцией степени на пространстве матриц размера );
${displaystyle det A^{T}=det A}$ (Определитель матрицы не меняется при её транспонировании);
(Определитель произведения матриц равен произведению их определителей, и — квадратные матрицы одного и того же порядка);
${displaystyle det A^{-1}=(det A)^{-1}}$ , причём матрица обратима тогда и только тогда, когда обратим её определитель ;
Существует ненулевое решение уравнения тогда и только тогда, когда (или же должен быть нетривиальным делителем нуля в случае, если — не целостное кольцо).

Определитель как функция строк (столбцов) матрицы[править | править код]

При изучении теории определителей полезно иметь в виду, что в основе этой теории лежит техника манипулирования со строками и столбцами матриц, разработанная К.Ф. Гауссом (преобразования Гаусса). Суть этих преобразований сводится к линейным операциям над строками (столбцами) и их перестановке. Эти преобразования достаточно простым образом отражаются на определителе, и при их изучении удобно “расчленить” исходную матрицу на строки (или столбцы) и считать определитель функцией, определённой над наборами строк (столбцов). Далее буквами ${displaystyle {hat {A}}_{i}}$ обозначаются строки (столбцы) матрицы .

1. Определитель — полилинейная функция строк (столбцов) матрицы. Полилинейность означает линейность функции по каждому аргументу при фиксированных значениях остальных аргументов:

${displaystyle det({hat {A}}_{1},ldots ,alpha {hat {A}}_{i}+beta {hat {A'}}_{i},ldots ,{hat {A}}_{n})=alpha det({hat {A}}_{1},ldots ,{hat {A}}_{i},ldots ,{hat {A}}_{n})+beta det({hat {A}}_{1},ldots ,{hat {A'}}_{i},ldots ,{hat {A}}_{n})}$

2. Определитель — кососимметрическая функция строк (столбцов) матрицы, то есть при перестановке двух строк (столбцов) матрицы её определитель умножается на −1:

${displaystyle det(ldots ,{hat {A}}_{i},ldots ,{hat {A}}_{j},ldots )=-det(ldots ,{hat {A}}_{j},ldots ,{hat {A}}_{i},ldots )}$

3. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю:

${displaystyle {hat {A}}_{i}={hat {A}}_{j}Longrightarrow det(ldots ,{hat {A}}_{i},ldots ,{hat {A}}_{j},ldots )=0}$

Замечание. Свойства 1-3 являются основными свойствами определителя как функции строк (столбцов), они легко доказываются непосредственно из определения. Свойство 2 (кососимметричность) является логическим следствием свойств 1 и 3. Свойство 3 является логическим следствием свойства 2, если в кольце элемент 2 (т.е. 1 + 1) не совпадает с нулём и не является делителем нуля. Из свойств 1 и 3 вытекают также следующие свойства:

4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя (следствие свойства 1).

5. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю (следствие свойства 4).

6. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю (следствие свойств 1 и 3).

7. При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится (следствие свойств 1 и 6).

Фактом, имеющим фундаментальное значение, является универсальность определителя как полилинейной кососимметрической функции полного ранга, аргументами которой являются элементы конечномерного векторного пространства (или -модуля с конечным базисом). Справедлива следующая

Теорема. Пусть

— свободный

-модуль ранга

(

-мерное векторное пространство над

, если

— поле). Пусть ${displaystyle varphi (X_{1},X_{2},dots ,X_{n})}$

—

-значная функция на ${displaystyle V^{n}}$

, обладающая свойствами 1-3. Тогда при выборе базиса ${displaystyle E_{1},E_{2},dots ,E_{n}}$

пространства

существует константа ${displaystyle c_{0}=varphi (E_{1},E_{2},dots ,E_{n})}$

такая, что при всех значениях ${displaystyle X_{1},X_{2},dots ,X_{n}}$

справедливо равенство:

${displaystyle varphi (X_{1},X_{2},dots ,X_{n})=c_{0}det({hat {X}}_{1},{hat {X}}_{2},dots ,{hat {X}}_{n})}$

где ${displaystyle {hat {X}}_{i}}$ — столбец координат вектора $X_{i}$ относительно базиса ${displaystyle E_{1},E_{2},dots ,E_{n}}$ .

Одним из важнейших следствий универсальности определителя является следующая теорема о мультипликативности определителя.

Теорема. Пусть

— матрица размера

. Тогда

для любой матрицы

размера

Доказательство

Рассмотрим на пространстве столбцов $R^{n}$ кососимметрическую полилинейную форму ${displaystyle varphi ({hat {X}}_{1},{hat {X}}_{2},dots ,{hat {X}}_{n})=det(A{hat {X}}_{1},A{hat {X}}_{2},dots ,A{hat {X}}_{n})=det(AX)}$ . Согласно доказанной теореме, эта форма равна ${displaystyle c_{0}det({hat {X}}_{1},{hat {X}}_{2},dots ,{hat {X}}_{n})=c_{0}det X}$ , где ${displaystyle c_{0}=varphi (E_{1},E_{2},dots ,E_{n})=det({hat {A}}_{1},{hat {A}}_{2},dots ,{hat {A}}_{n})=det A}$ .
■

Определитель и ориентированный объём[править | править код]

Пусть — три вектора в пространстве $mathbb {R} ^{3}$ . Они порождают параллелепипед, вершины которого лежат в точках с радиус-векторами . Этот параллелепипед может быть вырожден, если вектора компланарны (лежат в одной плоскости, линейно зависимы).

Функция ориентированного объёма определяется как объём параллелепипеда, порождённого этими векторами, и взятый со знаком “+”, если тройка векторов положительно ориентирована, и со знаком “-“, если она ориентирована отрицательно.
Функция полилинейна и кососимметрична. Свойство 3, очевидно, выполнено. Для доказательства полилинейности этой функции, достаточно доказать её линейность по вектору vec a . Если вектора линейно зависимы, значение будет нулевым независимо от вектора vec a , и значит, линейно зависящим от него. Если вектора линейно независимы, обозначим через вектор единичной нормали к плоскости векторов , такой, что . Тогда ориентированный объём параллелепипеда равен произведению площади основания, построенного на векторах и независящего от вектора vec a , и алгебраической величины проекции вектора vec a на нормаль к основанию, которая равна скалярному произведению и является величиной, линейно зависящей от вектора vec a . Линейность по vec a доказана, и аналогично доказывается линейность по остальным аргументам.

Применяя теорему об универсальности определителя как кососимметрической полилинейной функции, получаем, что при выборе ортонормированного базиса ${displaystyle ({vec {e}}_{1},{vec {e}}_{2},{vec {e}}_{3})}$ пространства $mathbb {R} ^{3}$

${displaystyle {rm {Vol}}({vec {a}},{vec {b}},{vec {c}})={rm {Vol}}({vec {e}}_{1},{vec {e}}_{2},{vec {e}}_{3})det {begin{pmatrix}a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}\a_{3}&b_{3}&c_{3}end{pmatrix}}=det {begin{pmatrix}a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}\a_{3}&b_{3}&c_{3}end{pmatrix}}}$

где $a_{i},b_{i},c_{i}$ — координаты векторов в выбранном базисе.

Таким образом, определитель матрицы коэффициентов векторов относительно ортонормированного базиса имеет смысл ориентированного объёма параллелепипеда, построенного на этих векторах.

Всё вышесказанное без существенных изменений переносится на пространство $mathbb {R} ^{n}$ произвольной размерности.

Разложение определителя по строке/столбцу и обращение матриц[править | править код]

Формулы разложения определителя по строке/столбцу позволяют сводить вычисление определителей к рекурсивной процедуре, использующей вычисление определителей меньших порядков. Для вывода этих формул сгруппируем и просуммируем в формуле для определителя матрицы ${displaystyle C=(c_{ij})}$ , с учётом равенства ${displaystyle varepsilon _{i_{1}dots i_{n-1}n}=varepsilon _{i_{1}dots i_{n-1}}}$ , все ненулевые члены, содержащие элемент ${displaystyle c_{nn}}$ . Эта сумма равна:

${displaystyle c_{nn}sum _{i_{1},dots i_{n-1}=1}^{n-1}varepsilon _{i_{1}dots i_{n-1}n}c_{1i_{1}}dots c_{n-1,i_{n-1}}=c_{nn}sum _{i_{1},dots i_{n-1}=1}^{n-1}varepsilon _{i_{1}dots i_{n-1}}c_{1i_{1}}dots c_{n-1,i_{n-1}}=c_{nn}det C_{n}^{n}}$

где ${displaystyle C_{i}^{j}}$ — матрица, получаемая из удалением строки с номером и столбца с номером .

Так как произвольный элемент $c_{ij}$ можно перестановками соответствующего столбца вправо и перестановками соответствующей строки вниз переместить в правый нижний угол матрицы, причём дополнительная к нему матрица сохранит свой вид, то сумма всех членов в разложении определителя, содержащих $c_{ij}$ , будет равна

${displaystyle (-1)^{(n-i)}(-1)^{(n-j)}c_{ij}det C_{i}^{j}=(-1)^{i+j}c_{ij}det C_{i}^{j}=c_{ij}A_{i}^{j}}$

Величина ${displaystyle A_{i}^{j}=(-1)^{i+j}det C_{i}^{j}}$ называется алгебраическим дополнением элемента матрицы $c_{ij}$ .

Учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из i-ой строки, можно разложить определитель по членам этой строки:

${displaystyle det C=sum _{j=1}^{n}c_{ij}A_{i}^{j}}$

— Формула разложения определителя по i-ой строке

Аналогично, учитывая, что каждый член разложения определителя с ненулевым коэффициентом содержит ровно один элемент из j-го столбца, можно разложить определитель по членам этого столбца:

${displaystyle det C=sum _{i=1}^{n}c_{ij}A_{i}^{j}}$

— Формула разложения определителя по j-ому столбцу

Если элементы k-й строки матрицы скопировать в i-ую строку, её определитель станет равен нулю, а по формуле разложения определителя по i-ой строке получится:

${displaystyle 0=sum _{j=1}^{n}c_{kj}A_{i}^{j}}$

— Формула “фальшивого” разложения определителя по i-ой строке (

Аналогично для столбцов:

${displaystyle 0=sum _{j=1}^{n}c_{ik}A_{i}^{j}}$

— Формула “фальшивого” разложения определителя по j-ому столбцу ( jne k

)

Полученные формулы полезно записать в матричном виде. Введём матрицу алгебраических дополнений к элементам матрицы : ${displaystyle A=(A_{i}^{j})}$ .
Тогда, согласно с полученными формулами,

${displaystyle CA^{T}=A^{T}C=(det C)cdot E}$

Следствие 1 (Критерий обратимости матриц). Квадратная матрица является обратимой тогда и только тогда, когда — обратимый элемент кольца , при этом ${displaystyle C^{-1}=(det C)^{-1}cdot A^{T}}$ .

Следствие 2. Если произведение матриц равно нулю , и матрица — квадратная, тогда .

Решение систем линейных алгебраических уравнений с помощью определителей[править | править код]

Формула Крамера позволяет выразить решение системы линейных алгебраических уравнений в виде отношения определителей, в знаменателе которого стоит определитель системы, а в числителе — определитель матрицы системы, в которой столбец коэффициентов при соответствующей переменной заменён на столбец из правых частей уравнений.

Формула Крамера. Пусть задана система линейных алгебраических уравнений в матричном виде: , где ${displaystyle C=(c_{ij})}$ — матрица коэффициентов системы размера , ${displaystyle B=(b_{1},b_{2},dots ,b_{n})^{T}}$ — столбец из правых частей уравнений системы, и вектор ${displaystyle X=(x_{1},x_{2},dots ,x_{n})^{T}}$ — решение этой системы. Тогда при любых ${displaystyle lambda _{1},lambda _{2},dots ,lambda _{n}in R}$ справедливо равенство:

${displaystyle (lambda _{1}x_{1}+lambda _{2}x_{2}+dots +lambda _{n}x_{n})cdot (det C)=-det {begin{pmatrix}c_{11}&c_{12}&dots &c_{1n}&b_{1}\c_{21}&c_{22}&dots &c_{2n}&b_{2}\dots &dots &dots &dots &dots \c_{n1}&c_{n2}&dots &c_{nn}&b_{n}\lambda _{1}&lambda _{2}&dots &lambda _{n}&0end{pmatrix}}}$

Из этой формулы следует, в частности, что если — не вырожден (не является нулём или делителем нуля), система может обладать не более чем одним решением, а если определитель ещё и обратим, то система обладает единственным решением.

Одной из важнейших теорем в теории определителей является следующая теорема о решениях однородной системы линейных уравнений.

Теорема. Пусть — поле. Однородная система линейных уравнений имеет нетривиальное (ненулевое) решение тогда и только тогда, когда определитель матрицы коэффициентов равен нулю: .

Доказательство

Необходимость условия содержится в следствии 2 предыдущего раздела. Докажем необходимость.

Если матрица — нулевая, любой вектор является решением.
Пусть $C_{0}$ — максимальный невырожденный минор в матрице имеет размеры . Не ограничивая общности, считаем, что этот минор образован первыми r строками и столбцами (иначе перенумеруем переменные и переставим уравнения в другом порядке.)
Введём вектора ${displaystyle X_{0}=(x_{1},x_{2},dots ,x_{r})^{T}}$ и ${displaystyle X_{1}=(x_{r+1},dots ,x_{n})^{T}}$ . Тогда первые r уравнений системы в матричном виде записываются так:

${displaystyle C_{0}X_{0}+C_{1}X_{1}=0}$

Поскольку матрица $C_{0}$ обратима, любому значению $X_{1}$ соответствует единственный вектор ${displaystyle X_{0}=-C_{0}^{-1}C_{1}X_{1}}$ , удовлетворяющий этим уравнениям. Покажем, что при этом остальные уравнения будут выполнены автоматически. Пусть .

Введём две матрицы:

${displaystyle D_{1}={begin{pmatrix}c_{11}&dots &c_{1r}&c_{1r+1}x_{r+1}+dots +c_{1n}x_{n}\c_{21}&dots &c_{2r}&c_{2r+1}x_{r+1}+dots +c_{2n}x_{n}\dots &dots &dots &dots dots dots dots \c_{r1}&dots &c_{rr}&c_{rr+1}x_{r+1}+dots +c_{rn}x_{n}\c_{j1}&dots &c_{jr}&c_{jr+1}x_{r+1}+dots +c_{jn}x_{n}\end{pmatrix}}}$

и ${displaystyle D_{2}={begin{pmatrix}c_{11}&dots &c_{1r}&c_{1r+1}x_{r+1}+dots +c_{1n}x_{n}\c_{21}&dots &c_{2r}&c_{2r+1}x_{r+1}+dots +c_{2n}x_{n}\dots &dots &dots &dots dots dots dots \c_{r1}&dots &c_{rr}&c_{rr+1}x_{r+1}+dots +c_{rn}x_{n}\c_{j1}&dots &c_{jr}&-(c_{j1}x_{1}+dots +c_{jr}x_{r})\end{pmatrix}}}$

У матрицы $D_{1}$ все столбцы являются частями столбцов из матрицы , а последний столбец есть линейная комбинация столбцов матрицы с коэффициентами ${displaystyle x_{r+1},dots ,x_{n}}$ , поэтому в силу линейности определителя по столбцам ${displaystyle det D_{1}}$ есть линейная комбинация определителей миноров матрицы размера . Так как $C_{0}$ — максимальный по размеру невырожденный минор, все миноры большего размера имеют нулевой определитель, поэтому ${displaystyle det D_{1}=0}$ .

Из соотношения ${displaystyle C_{0}X_{0}+C_{1}X_{1}=0}$ следует, что ${displaystyle D_{2}Y=0}$ , где столбец ${displaystyle Y=(x_{1},dots ,x_{r},1)^{T}neq 0}$ . Поэтому ${displaystyle det D_{2}=0}$ .

Тогда ${displaystyle 0=det D_{1}-det D_{2}=(det C_{0})cdot (c_{j1}x_{1}+c_{j2}x_{2}+dots +c_{jn}x_{n})}$ . И так как ${displaystyle det C_{0}neq 0}$ , то j-ое уравнение системы тоже выполнено. ■

Данная теорема используется, в частности, для нахождения собственных значений и собственных векторов матриц.

Критерий полноты и линейной независимости системы векторов[править | править код]

Тесно связанными с понятием определителя является понятие линейной зависимости и полноты систем векторов в векторном пространстве.

Пусть — поле, — векторное пространство над с конечным базисом ${displaystyle {vec {e_{1}}},{vec {e_{2}}},dots ,{vec {e_{n}}}}$ . Пусть задан ещё набор из векторов ${displaystyle {vec {v_{1}}},{vec {v_{2}}},dots ,{vec {v_{n}}}}$ . Их координатами ${displaystyle v_{ij}}$ относительно заданного базиса являются коэффициенты разложения ${displaystyle {vec {v_{i}}}=sum v_{ij}{vec {e_{j}}}}$ . Составим (квадратную) матрицу ${displaystyle A=(v_{ij})}$ . Справедлива теорема:

Теорема (Критерий полноты и линейной независимости системы векторов).

(1) Система векторов ${displaystyle {vec {v_{1}}},{vec {v_{2}}},dots ,{vec {v_{n}}}}$

линейно зависима тогда и только тогда, когда det A=0

(2) Система векторов ${displaystyle {vec {v_{1}}},{vec {v_{2}}},dots ,{vec {v_{n}}}}$

полна, тогда и только тогда, когда матрица

не вырождена (

Доказательство

(1) Доказательство основано на том, что вектор ${displaystyle sum x_{i}{vec {v_{i}}}}$ имеет столбец координат, равный , где ${displaystyle X=(x_{1},x_{2},dots ,x_{n})^{T}}$ .

Если ${displaystyle sum x_{i}{vec {v_{i}}}=0}$ , то AX=0 . Тогда и если отличен от нуля, то det A=0 .

Обратно, если det A=0 , существует ненулевой столбец , такой что AX=0 . Это означает, что ${displaystyle sum x_{i}{vec {v_{i}}}=0}$ .

(2) Если матрица не вырождена, она обратима. Пусть — произвольный вектор, ${displaystyle Y=(y_{1},y_{2},dots ,y_{n})^{T}}$ — столбец его координат, ${displaystyle X=A^{-1}Y=(x_{1},x_{2},dots ,x_{n})^{T}}$ . Тогда ${displaystyle {vec {u}}=sum x_{i}{vec {v_{i}}}}$ . Таким образом, произвольный вектор разложим по системы векторов ${displaystyle {vec {v_{1}}},{vec {v_{2}}},dots ,{vec {v_{n}}}}$ , что означает её полноту.

Обратно, пусть матрица вырождена. Тогда существует ненулевая строка коэффициентов ${displaystyle C=(c_{1},c_{2},dots ,c_{n})}$ , такая, что . Это значит, что любой вектор ${displaystyle {vec {u}}=sum x_{i}{vec {v_{i}}}}$ , разложимый по системе векторов ${displaystyle {vec {v_{1}}},{vec {v_{2}}},dots ,{vec {v_{n}}}}$ , удовлетворяет ограничению ${displaystyle c_{1}x_{1}+c_{2}x_{2}+dots +c_{n}x_{n}=0}$ . Если какой-то коэффициент $c_{k}$ отличен от нуля, то базисный вектор ${displaystyle {vec {e_{k}}}}$ не разложим по этой системе векторов, и значит, она не полна.
■

Следствие. В векторном пространстве , обладающем конечным базисом из векторов:

(1) всякая система, состоящая менее, чем из

векторов, не полна;

(2) всякая система, состоящая более, чем из

векторов, линейно зависима;

(3) всякий базис пространства

содержит ровно

векторов.

Таким образом, размерность векторного пространства с конечным базисом корректно определена.

Некоторые специальные свойства определителей[править | править код]

Определитель матрицы равен произведению её собственных значений.
Если квадратная матрица выражает линейное преобразование, то её определитель не меняется при замене базиса линейного пространства.

Алгоритмическая реализация[править | править код]

Прямые методы вычисления определителя могут быть основаны непосредственно на его определении, как суммы по перестановкам, или на разложении Лапласа по определителям меньшего порядка. Однако такие методы очень неэффективны, так как требуют О(n!) операций для вычисления определителя -го порядка. В то же время они универсальны, применимы в тех случаях, когда элементы матрицы не являются числами (функции, многочлены, дифференциальные формы чётной степени и т. д.), и не требуют выполнения операций деления.
Можно вычислить определитель и выполнив меньшее количество операций умножения; точнее, можно для матрицы обойтись лишь количеством слагаемых, равным количеству разбиений числа вместо , например 5 вместо 6 для ^[6]:

${displaystyle {begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}}=(a_{11}+a_{12})(a_{21}+a_{23})(a_{31}+a_{32})-a_{12}a_{21}(a_{31}+a_{32}+a_{33})-a_{13}(a_{21}+a_{22}+a_{23})a_{31}-(a_{11}+a_{12}+a_{13})a_{23}a_{32}+a_{11}a_{22}a_{33}}$ .
Один из наиболее быстрых численных методов вычисления определителя заключается в простой модификации метода Гаусса. Следуя методу Гаусса, произвольную матрицу можно привести к ступенчатому виду (Верхнетреугольная матрица), используя лишь две следующие операции над матрицей — перестановку двух строк и добавление к одной из строк матрицы другой строки, умноженной на произвольное число. Из свойств определителя следует, что вторая операция не изменяет определителя матрицы, а первая лишь меняет его знак на противоположный. Определитель матрицы, приведённой к ступенчатому виду, равен произведению элементов на её диагонали, так как она является треугольной, поэтому определитель исходной матрицы равен:

${displaystyle det A=(-1)^{s}cdot det A_{mbox{ref}},}$

где

— число перестановок строк, выполненных алгоритмом, а $A_{mbox{ref}}$

— ступенчатая форма матрицы

, полученная в результате работы алгоритма. Сложность этого метода, как и метода Гаусса, составляет $O(n^{3})$

, для его реализации необходимо использование операции деления.

Определитель можно вычислить, зная LU-разложение матрицы. Если , где и — треугольные матрицы, то . Определитель треугольной матрицы равен просто произведению её диагональных элементов.
Если доступен алгоритм, выполняющий умножение двух матриц порядка за время , где $M(n)geqslant n^{a}$ , для некоторого , то определитель матрицы порядка может быть вычислен за время .^[7] В частности это означает, что, используя для умножения матриц алгоритм Копперсмита — Винограда, определитель можно вычислить за время $O(n^{2.376})$ .

Специальные виды определителей[править | править код]

Определитель Вронского (Вронскиан)
Определитель Вандермонда
Определитель Грама
Определитель Якоби (Якобиан)

См. также[править | править код]

Циркулянт
Перманент
Пфаффиан
Результант

Примечания[править | править код]

↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — 13-е изд., исправленное. — М.: Наука, 1986.
↑ Э. И. Березкина. Математика древнего Китая. — М.: Наука, 1980.
↑ H. W. Eves. An Introduction to the History of Mathematics. — Saunders College Publishing, 1990.
↑ Скорняков Л. А. Элементы алгебры. — М.: Наука, 1986. — С. 16-23. — Тираж 21 000 экз.
↑ Определитель матрицы и геометрический смысл определителя матрицы (рус.). Математика для всех.
↑ Houston, Robin; Goucher, Adam P. & Johnston, Nathaniel (2023), A New Formula for the Determinant and Bounds on Its Tensor and Waring Ranks, arΧiv:2301.06586 [math.CO].
↑ J. R. Bunch and J.E. Hopcroft. Triangular factorization and inversion by fast matrix multiplication, Mathematics of Computation, 28 (1974) 231—236.

Литература[править | править код]

В. А. Ильин, Э. Г. Позняк Линейная алгебра, М.: Наука — Физматлит, 1999.
Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2000.
Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры: Учебник для вузов. М.: Физматлит, 2004.
Боревич З. И. Определители и матрицы. – М.: Наука, 1988.

Источник

Понятие и термины

Кроме математики, матрицы нашли широкое применение в физике и других прикладных науках. Используются они и в программировании, где их называют массивами. Большинство экономических моделей также описывается достаточно простой и компактной матричной формой.

Матрица состоит из столбцов (n) и строк (m). Характеризуется она порядком и размерностью. Обычно говорят, что некий массив В имеет размер m на n. Записывают это как В = {m х n}. Существует и другой вариант записи: В = (аij), где i и j – индексы, при этом 1≤ i ≤ m; 1 ≤ j ≤ n. В учебниках же просто указывается разрядность в виде 2х2, 3х3 и так далее. Матрица называется квадратной, если количество её строк равно величине столбцов.

Строки и столбцы начинают нумеровать сверху и с левой стороны. Если элементы массива равны нулю, то матрицу называют нулевой. Существует понятие главной диагонали. Располагается она сверху вниз слева. Расположенные на ней элементы называют диагональными. Когда они равны одному, а все остальные члены нулю, массив считается единичным.

Главной характеристикой массива является определитель, или детерминант. Им называют число, соответствующее алгебраической сумме всех возможных произведений столбцов на строки. Другими словами, чтобы найти значение детерминанта, нужно сумму элементов матрицы n умножить на её размерность m. При перемножении знак произведения определяется по числу инверсий. Их чётное количество соответствует положительному знаку, а нечётное – отрицательному.

Определитель — это число, которое определяет степень матрицы. Характеризуется он порядком. Так, определителем первого порядка называют значение, определяемое единственным элементом массива. Записывают его в виде выражения: A = {a}, detA = |A| = a.

С матрицами можно выполнять любые арифметические действия и даже возводить в степень. Определитель вычисляется только в квадратной матрице, то есть в той, у которой число строк равно числу столбцов. Расчёт проводится с использованием специальных операций. Нахождение определителя построено на использовании ряда аксиом, дающих возможность вычислить характеристику матрицы любого порядка.

Параметры определителя

Использование свойств определителей даёт возможность сделать процедуру их вычисления проще. Если взять множество натуральных чисел, записанных в порядке возрастания, K = {1, 2, 3, 4, …, n}, то с ними можно выполнить две операции: перестановку и транспозицию.

Под первой понимается упорядочение множеству чисел другой последовательности. Например, {1, 2, 3, 4} – {1, 4, 3, 2}. То есть {1, 2, 3, 4, …, n} – {k1, k2, k3, k4, …, kn}. Если же в последовательности изменяются только две позиции, а остальные остаются на своих местах, то такую операцию называют транспозицией {1, 2, 3, 4} – {1, 3, 2, 4}. Когда при перестановке нарушается порядок расположения, то множество содержит инверсию kj > ki (j < i).

При нахождении определителей используют следующие правила:

Детерминант транспонированной матрицы идентичен характеристике начальной матрицы.
Произведение элементов строки или столбца детерминанта на число S равнозначно умножению параметра на это же число. Это свойство позволяет выделить общий множитель массива.
При замене двух строк или двух столбцов между собой определитель инвертирует свой знак.
В нулевой матрице параметр будет равняться нулю.
Если в массиве порядок и размерность равны между собой, то значение параметра этой матрицы будет равно нулю.
Когда пара строк или столбцов массива пропорциональна относительно друг друга, то детерминант этой матрицы равняется нулю.
Параметр массива треугольного вида определяют как произведение элементов, находящихся на главной диагонали.
Если все члены строки (столбца) можно представить в виде сумм as j + bs j, то и характеристику можно найти как сумму принадлежащих определителей.
Значение параметра останется неизменным, если к элементам любого столбца или строки добавить соответствующие элементы иного столбца или строки после умножения на одну и ту же величину.
Общий определитель двух матриц равного порядка при их умножении определяется как произведение параметров.

Кроме этого, используется аксиома: если элементы в любой строке равны сумме пары слагаемых, то начальный детерминант определяется как сумма двух определителей. При этом на этой строке будут располагаться первые и вторые слагаемые, а оставшиеся строки совпадут с первоначальным значением.

Нахождение значения

Для того чтобы понять, как находить детерминант матрицы, следует понять способы решения простых матриц 2х2 и 3х3. Умея находить их параметр, несложно будет определить детерминант и массив более высокого порядка. В математике матрицу принято записывать в круглых скобках, а определитель в прямых. Обозначают детерминант в формулах как det.

Если дана матрица второго порядка, то есть 2х2, то её определитель ищут по формуле: det = ab – dc, где: а и d – элементы первой строки, b и c – члены второй строки. То есть определитель находят как разность произведений диагональных элементов между собой. Например, пусть задана матрица:

| 13 9 |

| 1 11 |

Её параметр будет равняться: det = 13 * 11 – 9 * 1 = 143 – 9 = 134.

Пусть дана некая матрица три на три:

(1 2 1)

(5 -1 -1)

(-2 2 5)

Необходимо найти её определитель. Для массива 3х3 детерминант можно найти двумя способами:

правилом Саррюса (треугольника);
универсальным методом.

Схематично первый способ можно представить следующим образом:

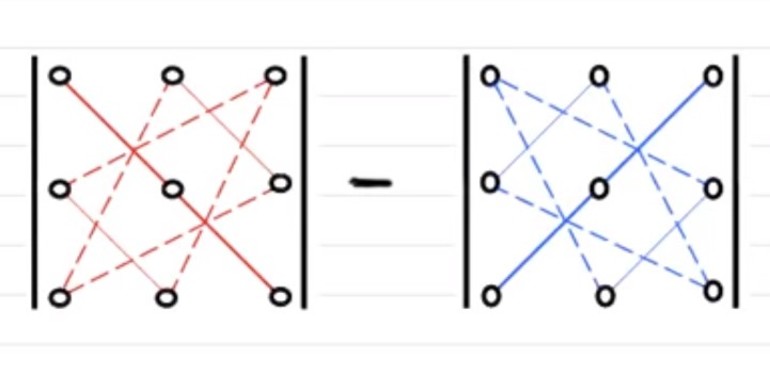
Для нахождения детерминанта по правилу треугольника нужно перемножить элементы массива, соединённые красными линиями, а затем их сложить. То же самое необходимо сделать с элементами, через которые проходит синяя линия. Затем из первого полученного значения вычесть второе. Вычитаемое и уменьшаемое состоит из трёх слагаемых. Определяются они двумя треугольниками и сумой элементов, стоящих на главной диагонали (сплошная линия).

Определитель будет равным: det = (1* (-1) * 5) + (5 * 2 * 1) + (2 * (-1) * (-2)) – (-2 * (-1) * (-1)) – (2 * 5 * 5) – (1 * 2 * (-1)) = – 5 + 10 + 4 – 2 – 20 + 2 = -11.

Второй способ проще. В его основе лежит метод разложения дискриминанта по первой строке или столбцу. То есть определитель можно найти по следующей формуле: det = a * n1 + b * n2 + c * n3, где: n1 – матрица 2х2, образованная с верхней левой части массива; n2 – матрица, полученная из второго и третьего члена первого столбца и третьего; n3 – массив, образованный из второго и третьего элемента первого столбца и третьего; a, b, c – элементы первой строчки.

Детерминант четвёртого порядка

Более сложной матрицей считается квадрат размером 4х4. Для подсчёта определителя нужно использовать универсальный способ нахождения детерминанта массива 3х3. То есть понадобится раскрыть первую строку и найти минор. Первый элемент в строке умножают на матрицу, образованную квадратом, начинающегося со второго члена следующего от него столбца.

Затем вычитают произведение второго элемента на алгебраическое дополнение, полученное путём вычёркивания первой строки и второго столбца. Далее, прибавляют третий элемент в первой строке и умножают на дополнение этого элемента. На последнем этапе вычитают четвёртый элемент верхней строки, умноженный на соответствующую ему дополнительную матрицу.

Теперь находят дискриминанты полученных матриц 3х3. Важно помнить, что знаки, стоящие перед алгебраическим дополнением, меняются. Если первый член имеет плюс, то перед вторым элементом ставится минус, перед третьим снова плюс и так далее.

Таким образом, массивы с высокими порядковыми номерами решаются методом понижения основного выражения. Если всё будет выполнено правильно, в ответе получится дискриминант, равный -13.

Например, для поиска определителя квадрата 6х6, нужно будет предварительно разложить систему по первой строке на массив низшего порядка 5х5, найти определитель матрицы 4х4, 3х3 и 2х2. Делая всё последовательно блочным методом, допустить ошибку практически невозможно. Если необходимо найти детерминант массивов десятого порядка и выше, то целесообразно находить определитель матрицы на онлайн-калькуляторе.

Стоит напомнить, что детерминант можно найти только для квадратного выражения в прямоугольной матрице. Правило нахождения определителя n порядка было предложено Лапласом. Он доказал и сформулировал теорему, гласящую о том, что величина определителей высшего порядка находится как сумма произведений частей какой-либо строки или столбца на принадлежащее им алгебраическое дополнение.

То есть выполняется разложение определителя по n строке или m столбцу.

Метод Гаусса

Способ Гаусса используется для решения системы уравнений. На их базе составляется массив. Первые столбцы образуют из коэффициентов, стоящих после неизвестных, а последний из значений, расположенных после знака равно. Для нахождения определителя этим способом необходимо выполнить два шага:

Привести матрицу к верхнетреугольной или нижнетреугольной форме путём элементарных преобразований.
Сосчитать произведение всех элементов, расположенных на главной диагонали треугольного массива, заменив при этом полученный знак определителя на противоположный.

Например, необходимо найти детерминант системы уравнений:

n1 + 2 * n2 – 3 * n3 = – 4.

2*n1 + 5 * n2 – 4 * n3 = 0.

-3*n1 + n2 – 3 * n3 = 5.

На первом этапе составляют матрицу и решают её. Выделяют первую строку и пытаются обнулить все первые коэффициенты. Для этого каждый элемент нужно умножить на такое число, чтобы последующий элемент обнулился. Затем берут другую строку и обнуляют уже вторые элементы. Так, для заданной системы уравнений первую строку необходимо умножить на -2, а затем сложить со второй строкой. То есть первый элемент в первом столбце будет равен: x11 = -2 * 1 + 2 = 0; второй: x22 = -2 * 2 +5 = 1; третий: x33 = -2*(-3) – 4 = 2; четвёртый: x44 = -2* (-4) + 0 = 8.

Аналогичные действия проводят по отношению к элементам третьей строки. Для обнуления первую строчку умножают уже не на -2, а на тройку. В результате первый столбец будет состоять из двух нулевых элементов. Затем переходят к обнулению элементов во втором столбце. Делают это последовательным умножением третьей строки на – 7. В итоге получится массив с тремя нулевыми членами.

Опираясь на полученную матрицу, составляют новую систему уравнений:

n1 + 2 * n2 – 3 * n3 = -4.

n2 – 2 * n3 = 8.

–20 * n3 = -63.

Затем из последнего равенства находят n3. Полученное значение подставляют во второе уравнение и определяют n2. На последнем этапе, используя найденные величины, вычисляют n1. Для нахождения детерминанта определяют тип матрицы, в этом случае она нижнетреугольная, и вычисляют его значение det = (1 * 1 * (-20)) = -20.

Найти детерминант небольшого ранга несложно. Но существуют задания, для решения которых нужно не только проявить внимание, но и потратить много времени. Для таких случаев существуют калькуляторы, помогающие выполнить вычисление определителя матрицы онлайн.

Кроме быстрого определения ответа, они также показывают подробное решение поставленной задачи. Если же доступа к интернету нет, то можно выполнить расчёт и в excel. Делается это с помощью функции «=МОПРЕД».

Источник

Приветствую всех. Сегодня мы познакомимся с понятием определителя матрицы. Узнаем что это, где он нам пригодится в дальнейшем и как его вычислить. Материал сам по себе достаточно необычный, но не особо сложный.

Определитель (детерминант) – основное понятие в теории линейной алгебры, используется для определения свойств матрицы.

Самое главное – определитель можно вычислить только для квадратной матрицы (количество строк равняется количеству столбцов). Чаще всего используют это понятие в решении “систем линейных алгебраических уравнений (СЛАУ)“, с которыми мы познакомимся в дальнейшем. А так же для характеристики СЛАУ и нахождения обратной матрицы, и много где ещё.

Вычисление определителя.

(1Х1)

Первым делом познакомимся с определителем первого порядка, точнее матрица один на один (1Х1).

Рассмотрели, что бы было. Это тоже нужно знать.

(2Х2)

Определитель второго порядка вычисляется по простому правилу. Произведение элементов главной диагонали минус произведение побочной.

Затруднений быть не должно, всё предельно просто.

(3Х3)

Методов нахождения определителя матрицы третьего порядка существует несколько, самых известных и наиболее часто используемых всего два, это:

Правило треугольника
Разложение по строке или столбцу

Правило (метод) треугольника.

Самый простой из всех трёх методов и одновременно с этим один из самых запутанных. Запутанный потому что могут возникать трудности при устном счёте.

Отсюда видно, что вычислений будет достаточно.

Проиллюстрируем на картинке.

Первый определитель соответствует первой скобке, второй определитель, второй скобке. Цветными линиями показаны элементы которые перемножаются, как видно из первого определителя, там все вычисления делаются относительно главной диагонали, во втором, относительно побочной диагонали.

Разложение по строке или столбцу.

Используется довольно редко, хоть и подходит для вычисления определителей любого порядка. Этот, как никакой другой, требует внимательности и понимания. Все вычисления как правило опираются на понятия алгебраического дополнения и минора. Пока что торопить события не будем, разберёмся с этими понятиями на практике, а сейчас попробуем разобраться без них. Для примера сделаем разложение по первой строке и запишем всё в общем виде.

Вот так должно быть выполнено в тетрадке, если просят всё расписать.

Небольшие пояснения. Мы сделали разложение по первой строке, следовательно мы будем вычёркивать подобным образом последовательно все элементы находящиеся в строчке от а11, до а13. Элементы находящийся на пересечении мы умножаем на получившуюся матрицу (2Х2). Минус единица в степени (i+j) записывается ВСЕГДА.

Таким образом мы имеем право делать разложение по любой строке или любому столбцу. Данный метод нас подводит к частным случаям упрощённого решения определителей.

На сегодня теории достаточно, в следующий раз будем заниматься практикой. Оставляйте свои комментарии. Спасибо за внимание.

Другие темы:

Источник

Определитель матрицы: алгоритм и примеры вычисления определителя матрицы

Перед тем как находить и считать определитель, дадим определение определителю матрицы.

Определение 1

Что такое определитель матрицы или детерминант матрицы? Определитель матрицы — это некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.

|А|, ∆, det A – символы, которыми обозначают определитель матрицы.

Как найти определитель матрицы? Вычислить определитель или найти определитель можно с помощью разных способов (в том числе онлайн и при помощи калькулятора). Конкретный способ поиска и того, как решать, выбирают в зависимости от порядка матрицы.

Пример 1

Определитель матрицы второго порядка можно вычислять по формуле:

А=1-231.

Решение матрицы:

det A=1-231=1×1-3×(-2)=1+6=7

Определитель матрицы 3-го порядка: правило треугольника

Нахождение определителя матрицы 3-го порядка осуществляется по одному из правил:

он может считаться по правилу треугольника;
расчет также проводится по правилу Саррюса.

Как найти определитель матрицы третьего порядка по методу треугольника (определитель матрицы 3×3)?

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 2

А=13402115-1

Решение:

det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

дописать слева от определителя два первых столбца;
перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 3

А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицы четвертого порядка, можно воспользоваться одним из 2-х способов:

разложением по элементам строки;
разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Пример 4

Разложение матрицы по элементам строки:

det A=ai1×Ai1+ai2×Ai2+…+аin×Аin

Разложение матрицы по элементам столбца:

det A=а1i×А1i+а2i×А2i+…+аni×Аni

Замечание

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Пример 5

А=01-132100-24513210

Решение:

раскладываем по 2-ой строке:

А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310

раскладываем по 4-му столбцу:

А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321

Свойства определителя

Свойства определителя:

если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
если поменять местами строки и столбцы, то знак поменяется на противоположный;
определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Замечание

В рамках темы советуем обратиться к модулю определителя.

Пример 6

А=134021005

Решение:

det А=134021005=1×5×2=10

Замечание

Матричныый определитель, который содержит нулевой столбец, равный нулю (представляет собой минор).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Загрузить PDF

Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение.

1
Запишите матрицу размерностью 3 x 3. Запишем матрицу размерностью 3 x 3, которую обозначим M, и найдем ее определитель |M|. Далее приводится общая форма записи матрицы, которую мы будем использовать, и матрица для нашего примера:
- $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{{23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2&4&7\4&6&2end{pmatrix}}$
2
Выберите строку или столбец матрицы. Эта строка (или столбец) будет опорной. Результат будет одинаков, независимо от того, какую строку или какой столбец вы выберете. В данном примере давайте возьмем первую строку. Чуть позже вы найдете несколько советов касательно того, как выбирать строку или столбец, чтобы упростить вычисления.
- Давайте выберем первую строку матрицы M в нашем примере. Обведите числа 1 5 3. В общей форме обведите a₁₁ a₁₂ a₁₃.
3
Зачеркните строку или столбец с первым элементом. Обратитесь к опорной строке (или к опорному столбцу) и выберите первый элемент. Проведите горизонтальную и вертикальную черту через этот элемент, вычеркнув таким образом столбец и строку с этим элементом. Должно остаться четыре числа. Будем считать эти элементы новой матрицей размерностью 2 x 2.
- В нашем примере, опорной строкой будет 1 5 3. Первый элемент находится на пересечении первого столбца и первой строки. Вычеркните строку и столбец с этим элементом, то есть первую сроку и первый столбец. Запишите оставшиеся элементы в виде матрицы 2 x 2:
- ~~1 5 3~~
- 2 4 7
- 4 6 2
4
Найдите определитель матрицы 2 x 2. Запомните, что определитель матрицы ${begin{pmatrix}a&b\c&dend{pmatrix}}$ вычисляется как ad – bc.^[1] Опираясь на это, вы можете вычислить определитель полученной матрицы 2 x 2, которую, если хотите, можете обозначить как X. Умножьте два числа матрицы X, соединенных по диагонали слева направо (то есть так: ). Затем вычтите результат умножения двух других чисел по диагонали справа налево (то есть так: / ). Используйте эту формулу, чтобы вычислить определитель матрицы, которую вы только что получили.
- В нашем примере определитель матрицы ${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4*2 – 7*6 = -34.
- Этот определитель называется минором элемента, который мы выбрали в нашей первоначальной матрице.^[2] Другими словами, мы только что нашли минор a₁₁.
5
Умножьте полученный ответ на выбранный элемент матрицы M. Вспомните, какой элемент из опорной строки (или столбца) мы использовали, когда вычеркивали другие элементы строки и столбца, чтобы получить новую матрицу. Умножьте этот элемент на полученный минор (определитель матрицы 2×2, которую мы обозначили X).
- В нашем примере мы выбирали элемент a₁₁, который равнялся 1. Умножим его на -34 (определитель матрицы 2×2), и у нас получится 1*-34 = -34.
6
Определите знак полученного результата. Далее вам понадобится умножить полученный результат на 1, либо на -1, чтобы получить алгебраическое дополнение (кофактор) выбранного элемента. Знак кофактора будет зависеть от того, в каком месте матрицы 3×3 стоит элемент. Запомните эту простую схему знаков, чтобы знать знак кофактора:
- + – +
- – + –
- + – +
- Поскольку мы работали с элементом a₁₁, для которого стоит знак +, то мы будем умножать полученное значение на +1 (то есть оставим его как есть). Алгебраическое дополнение нашего элемента будет равно -34.
- Вы также можете найти знак алгебраического дополнения по формуле (-1)^{i+j, где i и j – номер столбца и строки выбранного элемента соответственно.^[3]}
7

Повторите все вышеописанные действия со вторым элементом опорной строки (или столбца). Вернитесь к исходной матрице размерностью 3×3 и строке, которую мы обвели в самом начале вычислений. Повторите все действия с этим элементом:
8
Повторите с третьим элементом. Далее вам понадобится найти еще одно алгебраическое дополнение. Вычислите его для последнего элемента опорной строки или опорного столбца. Далее приводится краткое описание того, как вычисляется алгебраическое дополнение для a₁₃ в нашем примере:
- Зачеркните первую строку и третий столбец, чтобы получить матрицу ${begin{pmatrix}2&4\4&6end{pmatrix}}$
- Ее определитель равен 2*6 – 4*4 = -4.
- Умножьте результат на элемент a₁₃: -4 * 3 = -12.
- Элемент a₁₃ имеет знак + в приведенной выше таблице, поэтому ответ будет -12.
9
Сложите полученные результаты. Это последний шаг. Вам необходимо сложить полученные алгебраические дополнения элементов опорной строки (или опорного столбца). Сложите их вместе, и вы получите значение определителя матрицы 3×3.
- В нашем примере определитель равен -34 + 120 + -12 = 74.
Реклама

1
Выбирайте в качестве опорной строки (или столбца) ту, что имеет больше нулей. Помните, что в качестве опорной вы можете выбрать любую строку или столбец. Выбор опорной строки или столбца не влияет на результат. Если вы выберете строку с наибольшим количеством нулей, вам придется выполнять меньше вычислений, поскольку вам будет необходимо вычислить алгебраические дополнения только для ненулевых элементов. Вот почему:
- Допустим, вы выбрали 2 строку с элементами a₂₁, a₂₂, and a₂₃. Чтобы найти определитель, вам будет необходимо найти определители трех различных матриц размерностью 2×2. Давайте назовем их A₂₁, A₂₂, and A₂₃.
- То есть определитель матрицы 3×3 равен a₂₁|A₂₁| – a₂₂|A₂₂| + a₂₃|A₂₃|.
- Если оба элемента a₂₂ и a₂₃ равны 0, то наша формула становится намного короче a₂₁|A₂₁| – 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| – 0 + 0 = a₂₁|A₂₁|. То есть необходимо вычислить только алгебраическое дополнение одного элемента.
2

Используйте сложение строк, чтобы упростить матрицу. Если вы возьмете одну строку и прибавите к ней другую, то определитель матрицы не изменится. То же самое верно и для столбцов. Подобные действия можно выполнять несколько раз, кроме того, вы можете умножать значения строки на постоянную (перед сложением) для того, чтобы получить как можно больше нулей. Подобные действия могут сэкономить массу времени.
3
Помните, что вычислять определитель треугольных матриц намного проще. Определитель треугольных матриц вычисляется как произведение элементов на главной диагонали, от a₁₁ в верхнем левом углу до a₃₃ в нижнем правом углу. Речь в данном случае идет о треугольных матрицах размерностью 3×3. Треугольные матрицы могут быть следующих видов, в зависимости от расположения ненулевых значений:^[4]
- Верхняя треугольная матрица: Все ненулевые элементы находятся на главной диагонали и выше нее. Все элементы ниже главной диагонали равны нулю.
- Нижняя треугольная матрица: Все ненулевые элементы находятся ниже главной диагонали и на ней.
- Диагональная матрица: Все ненулевые элементы находятся на главной диагонали. Является частным случаем вышеописанных матриц.
Реклама

Советы

Описанный метод распространяется на квадратные матрицы любого ранга. Например, если вы используете его для матрицы 4×4, то после «вычеркивания» будут оставаться матрицы 3×3, для которых определитель будет вычисляться вышеупомянутым способом. Будьте готовы к тому, что вычислять определитель для матриц таких размерностей вручную — очень трудоемкая задача!
Если все элементы строки или столбца равны 0, то определитель матрицы тоже равен 0.

Об этой статье

Эту страницу просматривали 118 951 раз.

Была ли эта статья полезной?

Источник

История[править | править код]

Определения[править | править код]

Через перестановки[править | править код]

Аксиоматическое построение (определение на основе свойств)[править | править код]

Значение определителя матрицы[править | править код]

Матрицы 2 x 2[править | править код]

Матрицы 3 x 3[править | править код]

Матрицы N × N[править | править код]

Альтернативные методы вычисления[править | править код]

Основные свойства определителей[править | править код]

Определитель как функция строк (столбцов) матрицы[править | править код]

Определитель и ориентированный объём[править | править код]

Разложение определителя по строке/столбцу и обращение матриц[править | править код]

Решение систем линейных алгебраических уравнений с помощью определителей[править | править код]

Критерий полноты и линейной независимости системы векторов[править | править код]

Некоторые специальные свойства определителей[править | править код]

Алгоритмическая реализация[править | править код]

Специальные виды определителей[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Понятие и термины

Параметры определителя

Нахождение значения

Детерминант четвёртого порядка

Метод Гаусса

Вычисление определителя.

(1Х1)

(2Х2)

(3Х3)

Правило (метод) треугольника.

Разложение по строке или столбцу.

Определитель матрицы 3-го порядка: правило треугольника

Правило Саррюса

Методы разложения по элементам строки и столбца

Свойства определителя

Советы

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Мыши врачи как найти

Как составить текст письма деду морозу

Как составить заявку в банк на получение кредита

Добавить комментарий Отменить ответ