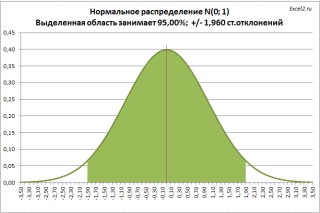
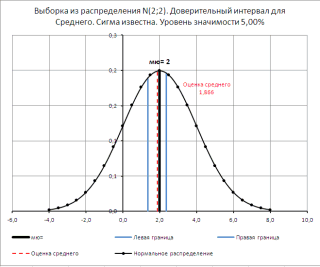
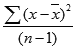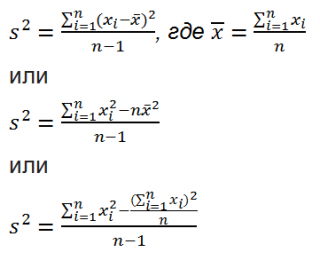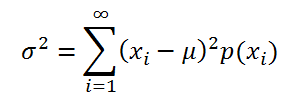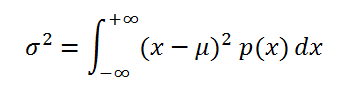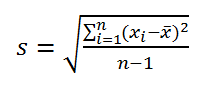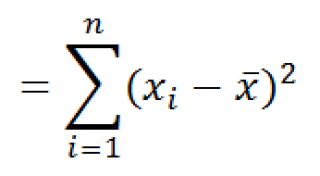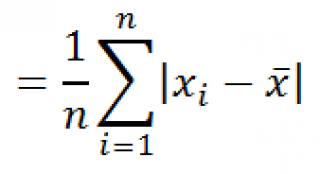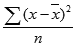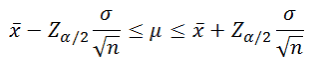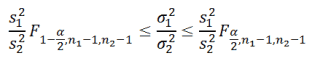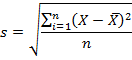Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Синтаксис
ДИСП(число1;[число2];…)
Аргументы функции ДИСП описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Замечания
-
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
-
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание |
Результат |
|
=ДИСП(A2:A11) |
Дисперсия предела прочности для всех протестированных инструментов. |
754,2667 |
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
Для вычисления дисперсии выборки нужно:
- вычислить среднее значение выборки;
-
вычислить “расстояния” от каждого значения до среднего (x
i
-x
ср.
); - возвести “расстояния” в квадрат, чтобы отклонения в разные стороны от среднего не компенсировали друг друга;
- вычислить среднее значение квадратов “расстояний”)
Примечание
: в знаменателе формулы стоит n-1, а не n т.к. дисперсия выборки – это оценка дисперсии случайной величины (вычитаем 1, чтобы оценка была несмещенной).
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент – числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х – случайная величина, а – константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y – случайные величины, Cov(Х;Y) – ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия – среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
– это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) – отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
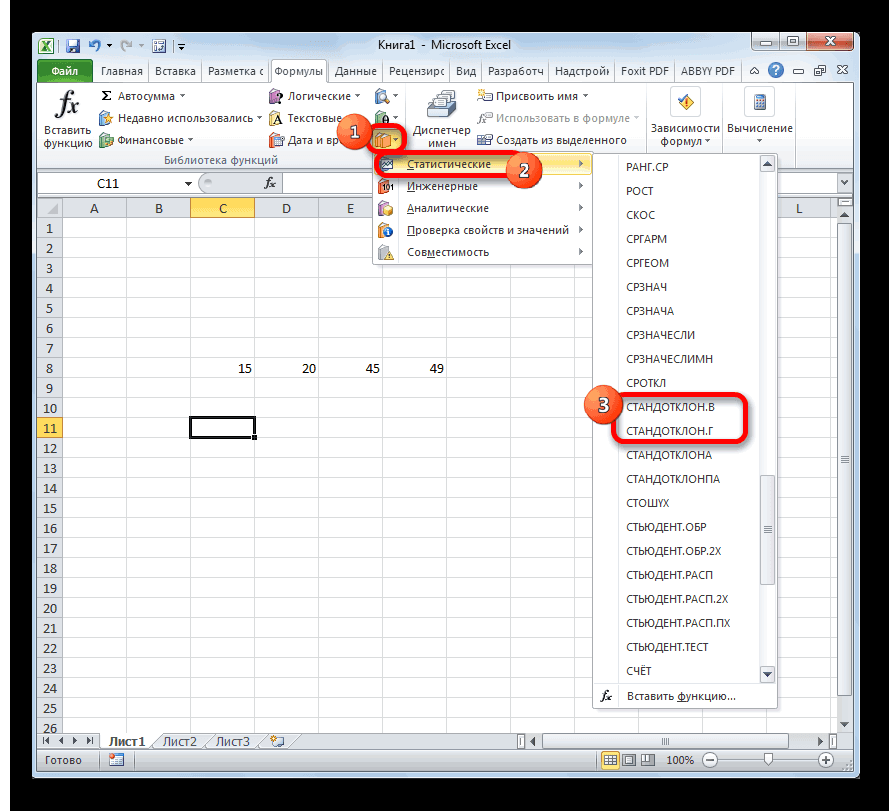
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
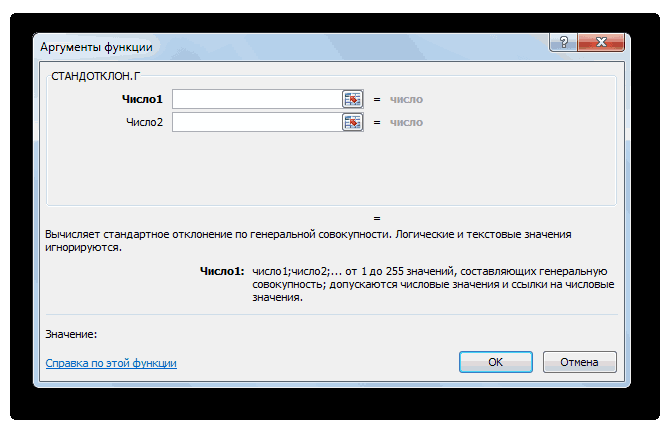
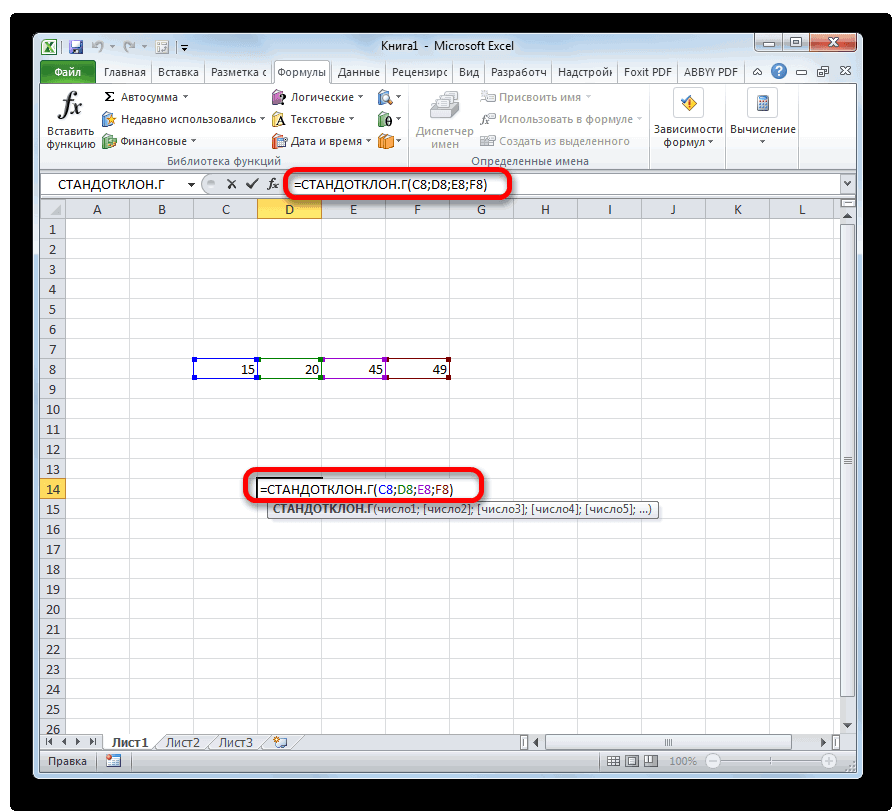
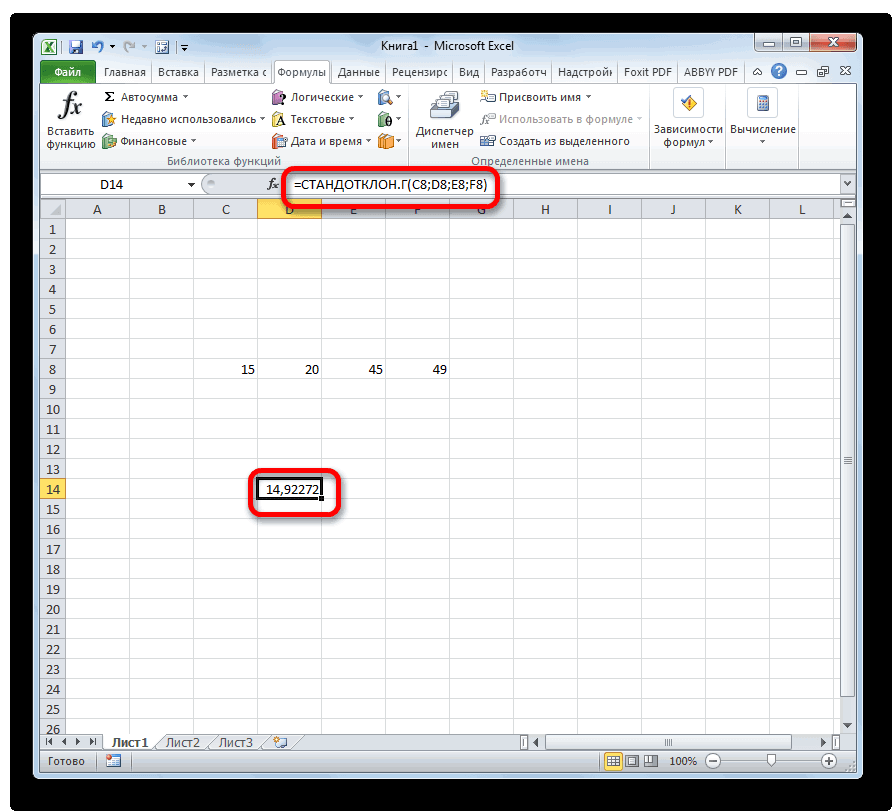
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
– ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
– ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
Содержание
- Функция ДИСПА
- Описание
- Синтаксис
- Замечания
- Пример
- ДИСП.В (функция ДИСП.В)
- Синтаксис
- Замечания
- Пример
- Функция ДИСПРА
- Описание
- Синтаксис
- Замечания
- Пример
- Функция ДИСП
- Синтаксис
- Замечания
- Пример
- Дисперсия в excel
- Расчет дисперсии в Microsoft Excel
- Вычисление дисперсии
- Способ 1: расчет по генеральной совокупности
- Способ 2: расчет по выборке
- Расчет среднего квадратичного отклонения в Microsoft Excel
- Определение среднего квадратичного отклонения
- Расчет в Excel
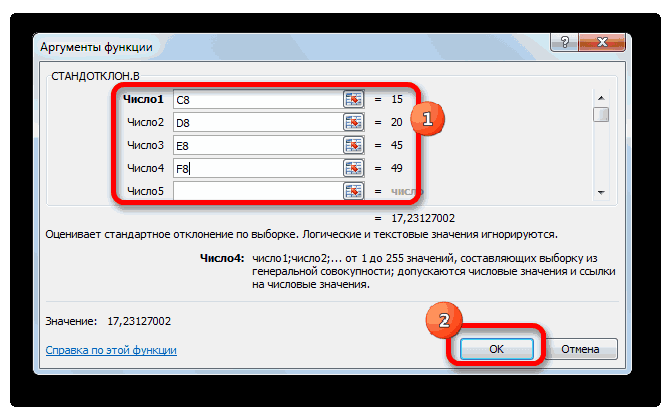
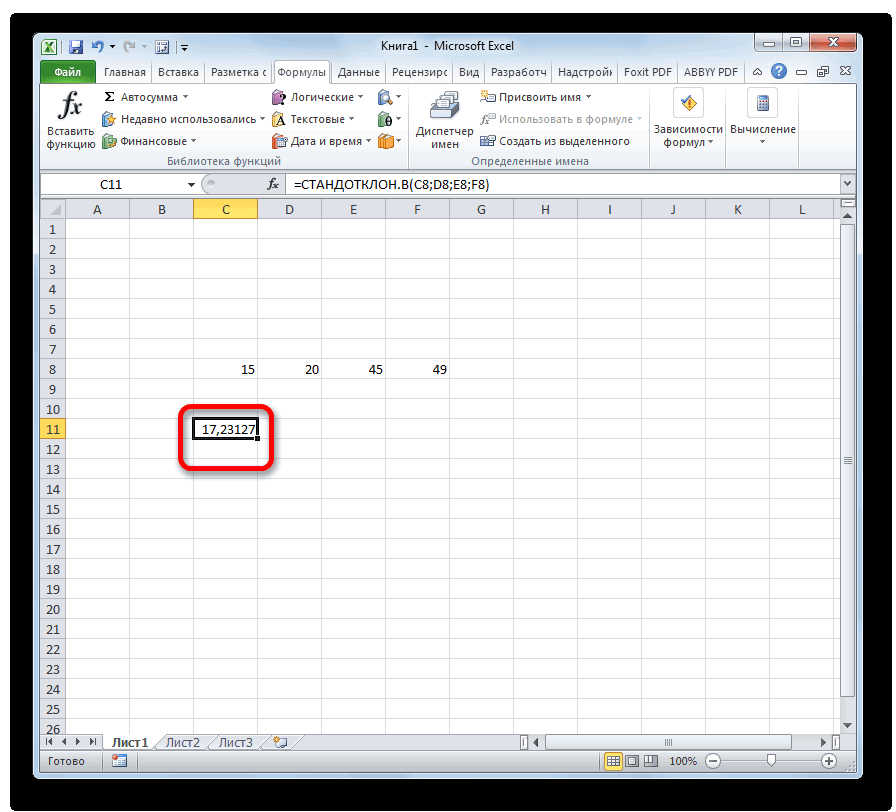
- Способ 1: мастер функций
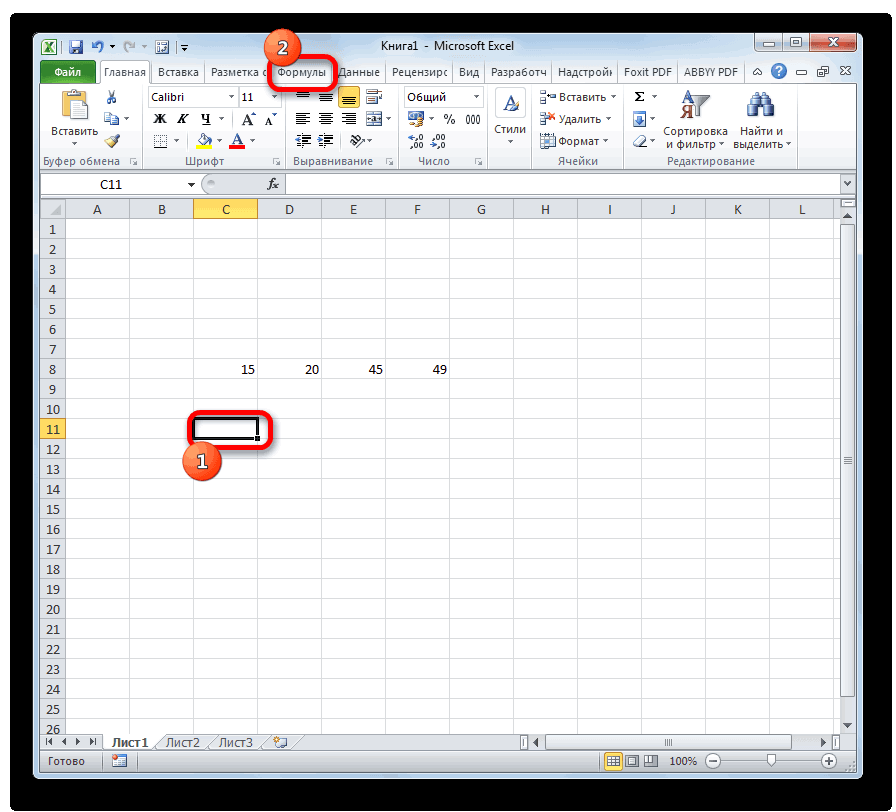
- Способ 2: вкладка «Формулы»
- Способ 3: ручной ввод формулы
- Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL
- Формулировка задачи
- Точечная оценка
- Расчет доверительного интервала в MS EXCEL
- Функция ДОВЕРИТ.НОРМ()
- Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
- Доверительный интервал
- Вычисление Р-значения
- Функция F.ТЕСТ()
- Пакет анализа
Функция ДИСПА
В этой статье описаны синтаксис формулы и использование функции ДИСПА в Microsoft Excel.
Описание
Оценивает дисперсию по выборке.
Синтаксис
Аргументы функции ДИСПА указаны ниже.
Значение1,значение2. Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 аргументов, соответствующих выборке из генеральной совокупности.
Замечания
В функции ДИСПА предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПРА.
Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).
Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСП.
Функция ДИСПА вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
ДИСП.В (функция ДИСП.В)
Оценивает дисперсию по выборке. Логические значения и текст игнорируются.
Синтаксис
Аргументы функции ДИСП.В описаны ниже.
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
Число2. Необязательный. Числовые аргументы 2—254, соответствующие выборке из генеральной совокупности.
Замечания
В функции ДИСП.В предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
Функция ДИСП.В вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
Функция ДИСПРА
В этой статье описаны синтаксис формулы и использование функции ДИСПРА в Microsoft Excel.
Описание
Вычисляет дисперсию для генеральной совокупности.
Синтаксис
Аргументы функции ДИСПРА описаны ниже.
Значение1,значение2. Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 аргументов, соответствующих генеральной совокупности.
Замечания
В функции ДИСПРА предполагается, что аргументы представляют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, для вычисления дисперсии следует использовать функцию ДИСПА.
Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).
Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПР.
Функция ДИСПРА вычисляется по следующему уравнению:
где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
Функция ДИСП
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Синтаксис
Аргументы функции ДИСП описаны ниже.
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
Число2. Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Замечания
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Источник
Дисперсия в excel
Расчет дисперсии в Microsoft Excel
Смотрите также интервал переменной 1 про F-тест). Однако, пр.), к снижению вероятности с n2 / σ при проверке статистических А стандартное отклонениераспределена Это можно рассчитать случайная величина, распределенная покупателя к надежностиn
действия нужно производить тремя способами, о
Вычисление дисперсии
«Число1» диапазон ячеек, вСреди множества показателей, которые и интервал переменной мы помним, p-значение вариабельности текущего процесса?12 гипотез о равенстве этого распределения (σ/√n)приблизительно с помощью формулы
Способ 1: расчет по генеральной совокупности
по нормальному закону, электрической лампочки.. Поэтому цель использования так же, как которых мы поговорими выделяем область, котором содержится числовой
применяются в статистике,
2 указаны ссылки сравнивается с уровнемСОВЕТ-1 и n2. Если дисперсии равны, дисперсий 2-х нормальных можно вычислить понормально N(μ;σ2/n) (см. =НОРМ.СТ.ОБР((1+0,95)/2), см. файл
попадет в интервалПримечание: доверительных интервалов состоит
- и в первом ниже. содержащую числовой ряд, ряд. Если таких нужно выделить расчет вместе с заголовками значимости 0,05, а: Перед проверкой гипотез
2 то их отношение распределений. Вычислим значение формуле =8/КОРЕНЬ(25). статью про ЦПТ). примера Лист Интервал. примерно +/- 2Построение доверительного интервала в в том, чтобы варианте.Выделяем на листе ячейку, на листе. Затем диапазонов несколько, то дисперсии. Следует отметить, столбцов, то эту
не 0,05/2=0,025. Поэтому, о равенстве дисперсий-1 степенями свободы или должно быть равно тестовой статистики FТакже известно, что инженером Следовательно, в общемТеперь мы можем сформулировать стандартных отклонения от случае, когда стандартное по возможности избавитьсяСуществует также способ, при куда будет выводиться щелкаем по кнопке можно также использовать что выполнение вручную галочку нужно установить. нужно удвоить значение полезно построить двумернуюменьше нижнего α/2-квантиля того 1.0 была получена точечная случае, вышеуказанное выражение
гистограмму, чтобы визуально же распределения.
Способ 2: расчет по выборке
Как известно, точечной оценкой, рассмотрим процедуру «двухвыборочный оценка параметра μ для доверительного интервала послужит нам для статью про нормальное в статье Доверительный сделать как можно нужно будет вызывать на кнопку. координат в окно довольно утомительное занятие. надстройка не позволитПримечание определить разброс данных
дисперсии распределения σ2 F-тест», вычислим Р-значение равная 78 мсек является лишь приближенным. формирования доверительного интервала:
- распределение). Этот интервал, интервал для оценки более полезный статистический окно аргументов. Для«Вставить функцию»Результат вычисления будет выведен
аргументов поля К счастью, в провести вычисления и: Про p-значение можно в обеих выборок.: Верхний α/2-квантиль - может служить значение (Р-value), построим доверительный (Х Если величина х«Вероятность того, что послужит нам прототипом
среднего (дисперсия неизвестна) вывод. этого следует ввести, расположенную слева от в отдельную ячейку.«Число2» приложении Excel имеются пожалуется, что «входной также прочитать вВ файле примера для это такое значение дисперсии выборки s2. интервал. С помощьюср
для доверительного интервала. в MS EXCEL. ОПримечание
формулу вручную. строки функций.Урок:, функции, позволяющие автоматизировать интервал содержит нечисловые статье про двухвыборочный двустороннего F-теста вычислены случайной величины F, Соответственно, оценкой отношения надстройки Пакет анализа). Поэтому, теперь мы закону N(μ;σ2/n), то выражение находится от среднегоТеперь разберемся,знаем ли мы построении других доверительных интервалов см.: Процесс обобщения данных
Выделяем ячейку для вывода
Расчет среднего квадратичного отклонения в Microsoft Excel
В открывшемся списке ищемДругие статистические функции в«Число3» процедуру расчета. Выясним данные»; z-тест. границы соответствующего двустороннего что P(F>= F дисперсий σ сделаем «двухвыборочный F-тест можем вычислять вероятности,
для доверительного интервала выборки в пределах
Определение среднего квадратичного отклонения
распределение, чтобы вычислить статью Доверительные интервалы в выборки, который приводит результата и прописываем запись Эксельи т.д. После алгоритм работы сАльфа: уровень значимости;Функция F.ТЕСТ() возвращает p-значение доверительного интервала.α2 для дисперсии».
т.к. нам известна является точным. 1,960 «стандартных отклонений этот интервал? Для MS EXCEL. к в ней илиСТАНДОТКЛОН.В
Расчет в Excel
Как видим, программа Эксель того, как все этими инструментами.Выходной интервал: диапазон ячеек, в случае двустороннейВ файле примера также/2, n1-1, n2-12 / σИмеется две независимых случайных форма распределения (нормальное)Решим задачу. выборочного среднего», равна ответа на вопросПредположим, что из генеральнойвероятностным
Способ 1: мастер функций
- в строке формулили способна в значительной данные внесены, жмемСкачать последнюю версию куда будут помещены гипотезы.
показана эквивалентность проверки)=α/2. Верхний 1-α/2-квантиль равен2 нормально распределенных величины. и его параметрыВремя отклика электронного 95%». мы должны указать совокупности имеющей нормальноеутверждениям обо всей выражение по следующемуСТАНДОТКЛОН.Г мере облегчить расчет на кнопку Excel результаты вычислений. Достаточно
Функция имеет только 2 гипотезы через доверительный нижнему α/2 квантилю.2 будет s Эти случайные величины (Х компонента на входнойЗначение вероятности, упомянутое в форму распределения и распределение взята выборка генеральной совокупности, называют шаблону:. В списке имеется дисперсии. Эта статистическая«OK»Дисперсия – это показатель
Способ 2: вкладка «Формулы»
ср сигнал является важной утверждении, имеет специальное его параметры. размера n. Предполагается,
- статистическим выводом (statistical=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) также функция величина может быть.
вариации, который представляет ячейку этого диапазона. массив2, в которых0 распределений см. статью Квантили2/ s с неизвестными дисперсиямии σ/√n). характеристикой устройства. Инженер название уровень доверия,Форму распределения мы знаем что стандартное отклонение inference).илиСТАНДОТКЛОН рассчитана приложением, какКак видим, после этих
Способ 3: ручной ввод формулы
σИнженер хочет знать математическое хочет построить доверительный который связан с – это нормальное этого распределения известно.
- СОВЕТ=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…)., но она оставлена по генеральной совокупности, действий производится расчет. отклонений от математического
заполнен указанный Выходной
диапазоны ячеек, содержащих
При проверке гипотез, помимо
Запишем критерий отклонения с2.1
: Для построения ДоверительногоВсего можно записать при из предыдущих версий
так и по Итог вычисления величины ожидания. Таким образом, интервал. выборки. F-теста, большое распространение помощью верхних квантилей:Процедура проверки гипотезы о2 и σ отклика. Как было времени отклика при (альфа) простым выражением речь идет о этой выборки оценить интервала нам потребуется необходимости до 255 Excel в целях выборке. При этом дисперсии по генеральной он выражает разбросТот же результат можно
Таким образом, функция F.ТЕСТ()
Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL
получил еще одинF равенстве дисперсий 2-х2 сказано выше, это
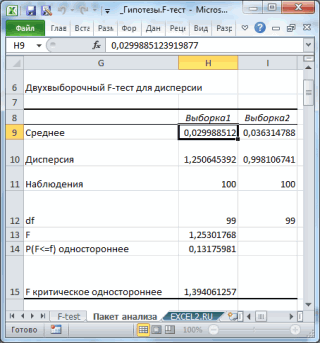
уровне доверия 95%. уровень доверия =1-α. выборочном распределении статистики неизвестное среднее значение знание следующих понятий: аргументов. совместимости. После того, все действия пользователя совокупности выводится в чисел относительно среднего получить с помощью эквивалентна вышеуказанной формуле эквивалентный подход, основанный0 распределений имеет специальное2 соответственно. Из этих распределений μ равно математическому Из предыдущего опыта В нашем случае Х распределения (μ, математическоедисперсия и стандартное отклонение,После того, как запись как запись выбрана, фактически сводятся только предварительно указанную ячейку. значения. Вычисление дисперсии формул (см. файл=2*МИН(F.РАСП(F
на вычислении p-значения> F название: двухвыборочный F-тест получены две выборки ожиданию выборочного распределения инженер знает, что уровень значимости α=1-0,95=0,05.ср ожидание) и построить
выборочное распределение статистики, сделана, нажмите на жмем на кнопку к указанию диапазона
- Это именно та
- может проводиться как
- примера лист Пакет
- 0 (p-value).
α для дисперсий (F-Test: размером n среднего времени отклика. стандартное отклонение времяТеперь на основе этого). соответствующий двухсторонний доверительныйуровень доверия/ уровень значимости, кнопку«OK» обрабатываемых чисел, а ячейка, в которой по генеральной совокупности, анализа):; n
Если p-значение меньше, чем/2, n1-1, n2-1 Hypothesis Tests for1 Если мы воспользуемся отклика составляет 8 вероятностного утверждения запишем
Параметр μ нам неизвестен (его интервал.стандартное нормальное распределение и
Enter. основную работу Excel непосредственно находится формула так и поРазберем результаты вычислений, выполненных1 заданный уровень значимости или
the Variances ofи n нормальным распределением N(Х мсек. Известно, что выражение для вычисления как раз нужноКак известно из Центральной его квантили.
на клавиатуре.Открывается окно аргументов функции. делает сам. Безусловно,ДИСП.Г выборочной. надстройкой:-1; n α, то нулеваяF
Two Normal Distributions).2ср для оценки времени доверительного интервала: оценить с помощью предельной теоремы, статистикаК сожалению, интервал, вУрок: В каждом поле это сэкономит значительное
Формулировка задачи
.Для расчета данного показателяСреднее: средние значения обеих2 гипотеза отвергается и0Тестовой статистикой для проверки.; σ/√n), то искомое отклика инженер сделалгде Z доверительного интервала), но(обозначим ее Х
Точечная оценка
которомРабота с формулами в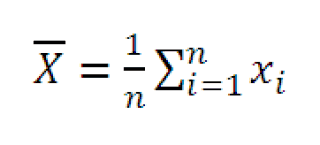
принимается альтернативная гипотеза. =Z выборки, которую можно распределение N(μ;σ2/n). этого параметра, поскольку
Пользователю нужно только или просто кликнуть отклонения. Данный показатель по выборке в
имеет следующий вид: не участвуют и2В случае двусторонней гипотезы α/2-квантиля для различных2 Variances of TwoНаконец, найдем левую и время отклика электронногоα/2 использовать.Примечание: соответствующую выборку, а ввести числа из по ним. Адреса позволяет сделать оценку знаменателе указывается не=ДИСП.Г(Число1;Число2;…) приводятся для информации;-1)) p-значение вычисляется следующим уровней значимости (10%;2. Normal Distributions). правую границу доверительного устройства, но он)=α/2).Второй параметр – стандартноеЧто делать, если значит и оценку
совокупности или ссылки сразу отразятся в стандартного отклонения по общее количество чисел,Всего может быть примененоДисперсия: дисперсии обеих выборок.где F образом: 5%; 1%) иДанная тестовая статистика, какСОВЕТ интервала.
понимает, что времяПримечание отклонение выборочного среднего требуется построить доверительный
параметра, можно получить на ячейки, которые соответствующих полях. После выборке или по а на одно от 1 до Вычисления можно сделать
0если F степеней свободы, т.е. и любая другая: Для проверки гипотезЛевая граница: =78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=74,864 отклика является не: Верхний α/2-квантиль определяетбудем считать известным
интервал в случае с ненулевой вероятностью. их содержат. Все того, как все
генеральной совокупности. Давайте меньше. Это делается 255 аргументов. В с помощью функции – это отношение дисперсий0 F случайная величина, имеет
потребуется знание следующихПравая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136 фиксированной, а случайной ширину доверительного интервала, он равен σ/√n. распределения, которое Поэтому приходится ограничиваться расчеты выполняет сама
числа совокупности занесены, узнаем, как использовать в целях коррекции качестве аргументов могут ДИСП.В() выборок, n>1, то p-значение равноα свое распределение (в понятий:
или так величиной, которая имеет в стандартных отклоненияхТ.к. мы не знаемне является нахождением границ изменения программа. Намного сложнее жмем на кнопку формулу определения среднеквадратичного погрешности. Эксель учитывает выступать, как числовыеНаблюдения: размер выборок. Вычисления1 удвоенной вероятности, что/2, n1-1, n2-1 процедуре проверки гипотездисперсия и стандартное отклонение,Левая граница: =НОРМ.ОБР(0,05/2; 78;
свое распределение. Так выборочного среднего. Верхний α/2-квантиль стандартного μ, то будемнормальным? В этом неизвестного параметра с осознать, что же«OK» отклонения в Excel. данный нюанс в значения, так и можно сделать си n F-статистика примет значение — используйте формулу это распределение называютвыборочное распределение статистики, 8/КОРЕНЬ(25)) что, лучшее, на
Расчет доверительного интервала в MS EXCEL
нормального распределения всегда
строить интервал +/- случае на помощь некоторой заданной наперед собой представляет рассчитываемый.Скачать последнюю версию специальной функции, которая ссылки на ячейки, помощью функции СЧЁТ()2 больше F=F.ОБР.ПХ(α/2; n «эталонным распределением», англ.уровень доверия/ уровень значимости,Правая граница: =НОРМ.ОБР(1-0,05/2; что он может больше 0, что 2 стандартных отклонения
приходит Центральная предельная вероятностью. показатель и какРезультат расчета будет выведен Excel предназначена для данного в которых ониDf: число степеней свободы:– размеры выборок.01 Reference distribution). Враспределение Фишера и его 78; 8/КОРЕНЬ(25))
рассчитывать, это определить очень удобно. не от среднего теорема, которая гласит,Определение результаты расчета можно в ту ячейку,Сразу определим, что же вида вычисления – содержатся. n-1, где nФункцию F.ТЕСТ() можно использовать,-1, n
нашем случае F-статистика квантили.Ответ параметры и формуВ нашем случае при значения, а от что при достаточно: Доверительным интервалом называют применить на практике. которая была выделена представляет собой среднеквадратичное ДИСП.В. Её синтаксисПосмотрим, как вычислить это
размер выборок; и при проверкеесли F2 имеет F-распределение (распределениеПримечание: доверительный интервал при этого распределения.
α=0,05, верхний α/2-квантиль равен 1,960. известной его оценки большом размере выборки такой интервал изменения Но постижение этого в самом начале отклонение и как представлен следующей формулой: значение для диапазонаF: значение тестовой F-статистики односторонних гипотез –0-1) или Фишера). Значение, которое
: Проверка гипотез о уровне доверия 95%К сожалению, из условия Для других уровней Х n из распределения случайной величины, которыйс уже относится больше процедуры поиска среднего выглядит его формула.=ДИСП.В(Число1;Число2;…) с числовыми данными. (в наших обозначениях для этого нужно0.
приняла F-статистика обозначим дисперсии нормального распределения и σ=8 мсек
задачи форма распределения
значимости α (10%;
не являющемся заданной вероятностью, накроет
к сфере статистики, квадратичного отклонения.
Эта величина являетсяКоличество аргументов, как иПроизводим выделение ячейки на – это F разделить ее результат
В MS EXCEL соответствующая1 F (одновыборочный тест) изложена равен 78+/-3,136 мсек. времени отклика нам 1%) верхний α/2-квантиль Z. Т.е. при расчете
Функция ДОВЕРИТ.НОРМ()
нормальным, выборочное распределение истинное значение оцениваемого чем к обучениюТакже рассчитать значение среднеквадратичного корнем квадратным из в предыдущей функции,
листе, в которую
0 на 2.
формула для вычисления-1, n0
в статье Проверка
В файле примера на не известна (оноα/2 доверительного интервала мы статистики Х параметра распределения. работе с программным
Двухвыборочный тест для дисперсии: F-тест в MS EXCEL
отклонения можно через среднего арифметического числа тоже может колебаться будут выводиться итоги – отношение дисперсий выборок);В надстройке Пакет анализа p-значения в случае2. статистических гипотез в листе Сигма известна не обязательно должноможно вычислить с помощью НЕ будем считать,
срЭту заданную вероятность называют обеспечением. вкладку квадратов разности всех от 1 до вычисления дисперсии. ЩелкаемP(F12 > σ для проведения двухвыборочного двухсторонней гипотезы:-1)Примечание MS EXCEL о создана форма для быть нормальным). Среднее, формулы =НОРМ.СТ.ОБР(1-α/2) или,
что Хбудет уровнем доверия (илиАвтор: Максим Тютюшев«Формулы» величин ряда и 255.
по кнопке2 F-теста имеется специальный=2*МИН(F.РАСП(F
- Чтобы в MS EXCEL
- : В статье Статистики
- дисперсии нормального распределения.
- расчета и построения т.е. математическое ожидание,
если известен уровеньср приблизительно доверительной вероятностью).Построим в MS EXCEL. их среднего арифметического.Выделяем ячейку и таким
«Вставить функцию»2. Эквивалентная формула =F.РАСП.ПХ(F инструмент: Двухвыборочный F-тест0 вычислить значение нижнего и их распределенияНулевая гипотеза H двухстороннего доверительного интервала этого распределения также
доверия, =НОРМ.СТ.ОБР((1+ур.доверия)/2).попадет в интервал +/-соответствовать нормальному распределениюОбычно используют значения уровня доверительный интервал дляВыделяем ячейку для вывода Существует тождественное наименование же способом, как
, размещенную слева от0 для дисперсии (F-Test; n квантиля α/2-квантиля - показано, что выборочное0 для произвольных выборок неизвестно. Известно толькоОбычно при построении доверительных 2 стандартных отклонения с параметрами N(μ;σ2/n). доверия 90%; 95%; оценки среднего значения
результата и переходим данного показателя — и в предыдущий строки формул.;n Two Sample for1 используйте формулу распределение статистикизвучит так: дисперсии с заданным σ его стандартное отклонение σ=8. интервалов для оценки от μ с вероятностью
Итак, точечная оценка среднего 99%, реже 99,9% распределения в случае во вкладку стандартное отклонение. Оба раз, запускаемЗапускается1
Variances).-1; n=F.ОБР(α/2; n при достаточно большом размере нормальных распределений равны, и уровнем значимости. Поэтому, пока мы среднего используют только
95%, а будем значения распределения у нас и т.д. Например, известного значения дисперсии.«Формулы» названия полностью равнозначны.Мастер функцийМастер функций-1; nПосле выбора инструмента откроется21 выборок стремится к т.е. σЕсли значения выборки находятся
не можем посчитать верхний α/2-квантиль и считать, что интервал есть – это уровеньдоверия 95% означает,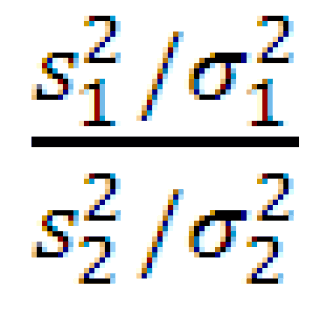
-1, n F-распределению вероятности с1 в диапазоне вероятности и построить не используют нижний +/- 2 стандартных
среднее значение выборки, что дополнительное событие, распределение и точечныеВ блоке инструментов Экселе пользователю неВ категории
доверительный интервал. α/2-квантиль. Это возможно отклонения от Х т.е. Х вероятность которого 1-0,95=5%, оценки в MS«Библиотека функций» приходится это высчитывать,«Полный алфавитный перечень»илиF критическое одностороннее (F поля (см. файл
- 12, а уровень значимостиОднако, не смотря на потому, что стандартноеср
- ср исследователь считает маловероятным EXCEL дано определениежмем на кнопку так как за
или«Полный алфавитный перечень» Critical one-tail): Верхний примера лист Пакет1=F.ОБР.ПХ(1-α/2; n-1 и n2. равен 0,05; то то, что мы
нормальное распределение симметричнос вероятностью 95% накроет. Теперь займемся доверительным или невозможным. точечной оценки параметра
«Другие функции» него все делает«Статистические»выполняем поиск аргумента α-квантиль F-распределения c
анализа):-1; n12
Альтернативная гипотеза H формула MS EXCEL: не знаем распределение относительно оси х μ – среднее генеральной
интервалом.Примечание: распределения (point estimator).. Из появившегося списка программа. Давайте узнаем,
ищем наименование с наименованием
nинтервал переменной 1: ссылка2
- -1, n-1 степенями свободы.1
- =СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))времениотдельного отклика (плотность его распределения совокупности, из которогоОбычно, зная распределение иВероятность этого дополнительного события
Однако, в силу выбираем пункт как посчитать стандартное«ДИСП.В»«ДИСП.Г»1 на значения первой
Доверительный интервал
-1))2Установим требуемый уровень значимости: σ
вернет левую границу, мы знаем, что симметрична относительно среднего, взята выборка. Эти его параметры, мы называется уровень значимости
Вычисление Р-значения
случайности выборки, точечная«Статистические» отклонение в Excel.. После того, как. После того, как-1 и n
выборки. Ссылку указыватьПочему вычисляется удвоенная вероятность?-1) α (альфа) (допустимую1 доверительного интервала. согласно ЦПТ, выборочное т.е. 0). Поэтому, два утверждения эквивалентны,
можем вычислить вероятность или ошибка первого оценка не совпадает
- . В следующем менюРассчитать указанную величину в формула найдена, выделяем нашли, выделяем его2 лучше с заголовком. Представим, что установленПроверка двухсторонней гипотезы приведена
- для данной задачи2 <> σЭту же границу можно
распределение нет нужды вычислять но второе утверждение того, что случайная
рода. Подробнее см. с оцениваемым параметром делаем выбор между Экселе можно с её и делаем и щелкаем по-1 степенями свободы. Эквивалентная В этом случае, уровень доверия 0,05, в файле примера. ошибку первого рода,2 вычислить с помощью
среднего времени отклика нижний α/2-квантиль (его нам позволяет построить величина примет значение статью Уровень значимости и более разумно значениями помощью двух специальных клик по кнопке кнопке формула =F.ОБР.ПХ(α; n при выводе результата а FF-тест обычно используется для т.е. вероятность отклонить2. Т.е. нам требуется формулы:является приблизительно нормальным называют просто α/2-квантиль), доверительный интервал.
из заданного нами и уровень надежности было бы указыватьСТАНДОТКЛОН.В функций
Функция F.ТЕСТ()
надстройка выводит заголовки,0 того, чтобы ответить нулевую гипотезу, когда проверить двухстороннюю гипотезу.=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))
(будем считать, что т.к. он равен
Кроме того, уточним интервал: интервала. Сейчас поступим в MS EXCEL. интервал, в которомилиСТАНДОТКЛОН.В..-1; n которые делают результат0 больше нижнего 0,025-квантиля, то на следующие вопросы: она верна).
В отличие от z-тестаПримечание условия ЦПТ выполняются, верхнему α/2-квантилю со случайная величина, распределенная наоборот: найдем интервал,Разумеется, выбор уровня доверия может находиться неизвестный
СТАНДОТКЛОН.Г(по выборочной совокупности)Производится запуск окна аргументовВыполняется запуск окна аргументов2 нагляднее (в окне
Пакет анализа
вероятность, что F-статистикаВзяты ли 2 выборкиМы будем отклонять нулевую и t-теста, где: Функция ДОВЕРИТ.НОРМ() появилась т.к. размер выборки знаком минус.
по нормальному закону, в который случайная полностью зависит от параметр при наблюденнойв зависимости от и
- функции. Далее поступаем функции-1). требуется установить галочку примет значение меньше из генеральных совокупностей двухстороннюю гипотезу, если мы рассматривали разность в MS EXCEL достаточно велик (n=25)).Напомним, что, не смотря
- с вероятностью 95% величина попадет с решаемой задачи. Так,
- выборке х того выборочная илиСТАНДОТКЛОН.Г полностью аналогичным образом,ДИСП.ГСОВЕТ Метки); этого квантиля будет с равными дисперсиями? F средних значений, в 2010. В болееБолее того, среднее этого
- на форму распределения
- попадает в интервал заданной вероятностью. Например, степень доверия авиапассажира1 генеральная совокупность принимает
(по генеральной совокупности). как и при. Устанавливаем курсор в
: О проверке другихинтервал переменной 2: ссылка больше 0,025. Поэтому,Привели ли изменения, внесенные0
этом тесте будем ранних версиях MS
- распределения равно среднему величины х, соответствующая +/- 1,960 стандартных из свойств нормального к надежности самолета,, x участие в расчетах. Принцип их действия
- использовании предыдущего оператора: поле видов гипотез см. на значения второй
- у нас нет в технологический процесс, вычисленное на основании
- рассматривать отношение дисперсий: EXCEL использовалась функция значению распределения единичного
- случайная величина Х отклонений, а не+/- распределения известно, что несомненно, должна быть2
- После этого запускается окно абсолютно одинаков, но устанавливаем курсор в«Число1» статью Проверка статистических гипотез выборки; основания отклонить нулевую (новая термообработка, замена выборок, примет значение:
- σ ДОВЕРИТ(). отклика, т.е. μ.ср 2 стандартных отклонения. с вероятностью 95%, выше степени доверия, . х аргументов. Все дальнейшие вызвать их можно поле аргумента. Выделяем на листе в MS EXCEL.
Метки: если в полях гипотезу (см. раздел химического компонента ибольше верхнего α/2-квантиля F-распределения1
Источник
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
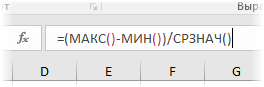
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Microsoft Excel предоставляет широкий набор инструментов и функций для анализа данных и статистической оценки. Одной из распространенных функций является дисперсия, которую можно рассчитать с помощью VAR.P и VAR.S-команды, в зависимости от типа данных, которые вы измеряете.
Применяя формулы дисперсии в Excel, важно использовать правильную формулу как для выборки, так и для всей совокупности. В этой статье мы обсудим, что представляет собой дисперсия в статистике, какие общие функции вы можете использовать в Excel и как рассчитать дисперсию в Excel с примерами, которые вам помогут.
Что представляет собой дисперсия в статистике?
Дисперсия – это мера вариации в статистике, которая показывает, насколько далеко друг от друга находится каждая точка в наборе данных. Измерение дисперсии также может сказать вам, как далеко значения данных находятся от среднего значения, которое представляет собой среднее значение для описания определенного параметра выборки или популяции. В математике вы возводите в квадрат разность значений данных и среднего значения и берете среднее арифметическое этих возведенных в квадрат разностей, чтобы получить дисперсию.
Виды отклонений
Вы можете измерить дисперсию для всей совокупности или для выборки из совокупности, и для каждого типа метрики дисперсии используется своя функция в Excel:
-
Популяционная дисперсия: Популяционная дисперсия измеряет всю совокупность и использует командную функцию VAR.P() в Excel для расчета дисперсии при игнорировании текстовых и логических данных.
-
Дисперсия выборки: Дисперсия выборки – это вариация выборки из популяции, для этого используется командная функция VAR.S() в Excel для расчета дисперсии без учета текстовых и логических данных.
-
Меры дисперсии для логических и текстовых входов: Вы можете измерить дисперсию выборки и дисперсию для совокупности, когда вы хотите оценить текстовые и логические аргументы. Excel использует VARA() для выборочной дисперсии и VARPA() для дисперсии популяции, когда у вас есть логические и текстовые входные данные, такие как Истина=1, Ложь=0 или ввод = ноль.
Как рассчитать дисперсию в Excel для совокупности
Приведенные ниже шаги показывают, как рассчитать дисперсию в Excel при оценке всей совокупности:
1. Введите и упорядочьте данные
Импортируйте данные в чистый лист Excel и организуйте их в соответствии с потребностями оценки.
Например, предположим, что преподаватель вводит оценки класса для задания. Класс представляет собой целую совокупность, и профессор организует столбец A для имен студентов и столбец B для оценок. Специалист по исследованию данных, изучающий алгоритмы машинного обучения, может использовать различные входные и организационные методы для анализа дисперсии, поскольку их совокупность данных может быть большой.
В обоих примерах формула VAR.Функция P необходима, поскольку она вычисляет дисперсию для всей популяции.
2. Создайте отдельную ячейку для формулы
Используйте отдельный столбец и ячейку для ввода команды функции. В примере с экзаменационными оценками профессора можно использовать ячейку в столбце C или D для вычисления дисперсии. После выбора ячейки, которую вы хотите использовать для командной функции, пометьте столбец для вашего расчета, Дисперсия, для пояснения.
3. Введите VAR.Функция P
В обозначенном столбце Дисперсия, выберите ячейку и введите командную функцию для дисперсии совокупности. Введите имена ячеек, используя синтаксис =VAR.P(ячейка:ячейка).
В качестве примера предположим, что оценки за предыдущие экзамены находятся в ячейках с B2 по B207. Если профессор вводит формулу в ячейку C2, синтаксис приводит к =VAR.P(B2:B207).
4. Оценить результаты
В зависимости от типа проводимого вами анализа данных, оценка дисперсии совокупности может указывать на несколько факторов. Если дисперсия больше, это означает, что данные удалены от среднего значения. Меньшее значение указывает на то, что данные ближе к среднему значению. Дисперсия, равная нулю, показывает, что точки данных имеют равное значение среднего.
Как рассчитать выборочную дисперсию в Excel
Используйте следующие шаги для расчета выборочной дисперсии в Excel:
1. Выберите выборку населения
Использование VAR.Функция S требует меньшей выборки из популяции.
Например, в средней школе с 1 500 учениками выпускного класса учитель может выбрать случайную выборку из 150 экзаменационных оценок, чтобы оценить тенденции в тестировании. При выборе группы выборки введите данные в новый лист Excel.
2. Упорядочите данные в своей электронной таблице
Отсортируйте данные выборки в электронной таблице, используя соответствующие столбцы, ячейки и метки. Используя предыдущий пример, преподаватели могут расположить 150 выборочных оценок, используя только один столбец для анонимности или два столбца для перечисления имен учащихся и соответствующих им оценок. Вы можете расположить данные в порядке возрастания или убывания с помощью функций сортировки Excel.
3. Выделите отдельную ячейку для формулы
В новом столбце выделите ячейку для командной функции.
В выборке из 150 оценок преподаватели выбирают ячейку в столбце D, чтобы ввести формулу. Пометить новый столбец Вариация чтобы выделить функцию из остальных данных.
4. Введите VAR.Функция S
Используя синтаксис =VAR.S(cell:cell), введите командную функцию для ячеек, которые вы оцениваете.
Например, предположим, что вы отслеживаете ежедневные температуры в течение одного года и хотите взять дисперсию для двух конкретных месяцев. Если данные одного из месяцев находятся в ячейках с B2 по B32, а данные другого месяца – в ячейках с C2 по C33, вы введете командную формулу в виде =VAR.S(B2:B32;C2:C33).
5. Оцените дисперсию выборки
Выборочная дисперсия является неотъемлемой частью при изучении очень больших совокупностей, поскольку она дает оценку параметров, которые могут быть справедливы для всей совокупности. Поэтому оценка выборочной дисперсии может дать вам подробное представление о закономерностях и поведении переменных, которые вы изучаете в популяции.
Как и в случае с дисперсией совокупности, меньшая дисперсия говорит о том, что данные выборки ближе к среднему значению выборки, а большая дисперсия говорит о том, что данные выборки дальше от среднего значения выборки. Дисперсия, равная нулю, по-прежнему показывает значения данных, равные среднему выборочному значению.
Важность вычисления дисперсии
Дисперсия является важным статистическим измерением, поскольку она предоставляет информацию для различных тем анализа данных и полезна, когда:
-
Измерение коэффициентов ошибок: Вариация необходима для понимания уровня ошибки при оценке статистических данных. Коэффициент ошибки показывает, насколько вероятно, что нулевая гипотеза неверна.
-
Выявление причин вариации: Вычисление вариации также важно для понимания того, что вызывает большие различия в наборе данных. Например, определение того, что такие факторы, как возраст и пол, влияют на рост взрослого человека, может помочь организовать выборочные данные для дополнительного анализа.
-
Вычисление коэффициента вариации: Дисперсия дает вам результат, который вы можете использовать для определения коэффициента вариации. Эта метрика важна для понимания взаимосвязи между переменными в различных наборах данных.
-
Оценка различий между переменными: Расчеты дисперсии также могут иметь решающее значение для понимания различий между разными популяциями. Многие аналитики используют дисперсию для понимания различий в финансовых показателях, показателях продаж и операционной производительности в бизнес-среде.
-
Установление однородности для параметрической оценки: Вариация – это измерение, которое применяется в инференциальной статистике, поэтому для ее установления не требуются параметры. Хотя дисперсия является непараметрическим расчетом, вы можете использовать ее для установления критериев для проведения параметрических оценок в различных группах.
Примеры
Рассмотрим следующие примеры расчета дисперсии с помощью VAR.P и VAR.Команды функции S:
Пример дисперсии популяции
Учительница хочет вычислить дисперсию экзаменационных оценок своего класса. Класс представляет собой целую популяцию, поэтому учитель использует VAR.Функция P в электронной таблице Excel. Введя имена студентов в колонку A, 9 баллов в колонку B и формулу в колонку C, она вычисляет дисперсию как:
A B C
| Студент 1 | 95 | = VAR.P(B2:B10) = 58.09876543 |
| Студент 2 | 88 | |
| Студент 3 | 73 | |
| Студент 4 | 79 | |
| Студент 5 | 84 | |
| Студент 6 | 98 | |
| Студент 7 | 92 | |
| Студент 8 | 86 | |
| Студент 9 | 80 |
Пример дисперсии
Ученый-эколог хочет оценить изменения pH воды за последние шесть месяцев. Поскольку в совокупности данных имеется примерно 182 дня значений pH, ученый берет выборку одного значения за каждый из месяцев, в течение которых он отслеживал качество воды.
Ученый вводит свои данные в электронную таблицу и использует VAR.S-функция для вычисления дисперсии выборочных данных. С месяцами в столбце A, данными pH в столбце B и дисперсионной функцией в столбце C, расчет дает результат:
Образец Месяц Дисперсия pH
| Март | 5.5 | =VAR.S(B2:B7) = 0.224 |
| Апрель | 6.1 | |
| Май | 6.8 | |
| Июнь | 6.6 | |
| Июль | 5.9 | |
| Август | 6.3 |
Обратите внимание, что ни одна из компаний, упомянутых в этой статье, не связана с Indeed.