Как найти дисперсию адекватности

3.7.1. Проверка адекватности системы

Первый
вопрос, который нас интересует после
проведения эксперимента и вычисления
коэффициентов модели – это проверка
адекватности. С этой целью вычисляем
остаточную
дисперсию
или дисперсию адекватности:

,

где
— количество опытов в эксперименте;

—количество
факторов;

—экспериментальные
значения отклика;

—величина
отклика, предсказанная уравнением
регрессии.

Для
проверки гипотезы об адекватности
модели пользуются
–
критерием Фишера, т.е. вычисляется
соотношение:

,

где
—
это выборочная дисперсия, которая
вычисляется по формуле:

,

где
— количество повторений одного опыта;

—экспериментальное
значение отклика в
-м
опыте при-м
наблюдении;

.

Если
рассчитанное значение
– критерия не превышает табличного, то
с соответствующей доверительной
вероятностью модель можно считать
адекватной.

Рассмотренный
способ расчета дисперсии адекватности
применим в случае, если опыты в матрице
планирования не дублируются, а информация
о выборочной дисперсии извлекается из
параллельных опытов в нулевой точке
или из предварительных экспериментов.
В общем случае,

,

где
— число повторений-го
опыта;

—среднее
арифметическое отклика из
параллельных опытов.

Здесь
смысл введения
в формулу заключается в следующем:
различию между экспериментальным и
расчетным значением придается тем
больший вес, чем больше число повторных
опытов.

Адекватность
линейного уравнения можно проверить и
другим путем. Очевидно, что коэффициент
,
определенный по результатам полного
или дробного факторного эксперимента,
всегда является оценкой:

.

С
другой стороны, величина
является оценкой результата опыта на
основном уровне. Поэтому, если выполнить
опыт на основном уровне, т.е. получитьи найти разницу,
то эта величина является оценкой суммы
квадратичных членов в уравнении
регрессии. Если разностьвелика, линейным уравнением пользоваться
нельзя, если мала – возможность
использования линейного уравнения не
исключена. Значимость различия можно
оценить по критерию Стьюдента:

,

где
— выборочное среднеквадратическое
отклонение.

Гипотеза
об адекватности уравнения принимается
в случае, когда
.

3.7.2. Проверка значимости коэффициентов

Проверка
значимости коэффициентов регрессии
осуществляется двумя равноценными
способами: проверкой по
– критерию Стьюдента или построением
доверительного интервала.

Сначала
находятся оценки дисперсии коэффициентов
регрессии
,
т.е. дисперсии всех коэффициентов равны
друг другу, так как они зависят только
от ошибки опыта и числа опытов. Затем
вычисляетсяпо уравнению:

.

Факторы,
имеющие большие значения
,
оказывают более существенное влияние
на процесс. Если,
то соответствующий коэффициент регрессии
незначим.

Проверку
значимости коэффициентов регрессии
можно осуществлять и построением
доверительного интервала. В случае
ортогонального планирования первого
порядка доверительный интервал
равен:

.

Коэффициент
значим, если его абсолютная величина
больше доверительного интервала.

Если
некоторые коэффициенты регрессии
признаны незначимыми, то соответствующие
факторы могут быть выведены из состава
уравнения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Совокупность действий, связанных с составлением уравнения регрессии, называется регрессионным анализом. Регрессионный анализ результатов однофакторного эксперимента включает в себя следующие действия:

1) подбор вида уравнения регрессии. Осуществляется с помощью, например, функциональных шкал;

2) определение постоянных коэффициентов в уравнении регрессии. Осуществляется с помощью МНК;

3) проверку соответствия (адекватности) уравнения регрессии результатам опытов.

Проверка адекватности уравнения регрессии результатам опытов проводится следующим образом:

1) По результатам повторных изменений в каждом опыте вычисляются дисперсия функции отклика (σ_у²), среднеквадратичная погрешность (), доверительный интервал 9), математическое ожидание ().

2) Осуществляется проверка однородности дисперсии , где j = 1,2,…, N – число опытов. Дисперсии  называются однородными, если при неограниченном увеличении числа повторных измерений п в каждом из опытов они стремятся к общему пределу, т.е.

.

Дисперсии проверяются на однородность с помощью критериев Фишера, Кохрена, Бартлета. Наиболее просто осуществить проверку однородности с помощью критерия Фишера. Для этого из всех дисперсий () выбирают две: наибольшую () и наименьшую ().

Отношение / сравнивают с табличным значением критерия Фишера (F):

· если /< F – дисперсии  и  однородны, следовательно, однородны и все дисперсии, лежащие в промежутке <<;

· если /> F – дисперсии неоднородны.

Значения критерия Фишера берутся из таблицы 2.3, составленной при доверительной вероятности Р = 0,95, для числа степеней свободы числителя (дисперсии ) и числа степеней свободы знаменателя (дисперсии ).

Таблица 2.3

Если в каждом из опытов число повторных измерений одинаково и равно п, то f_числ = f_знам = п – 1.

Если дисперсии  и неоднородны, то это означает, что число повторных измерений недостаточно или что среди результатов повторных измерений опыта с дисперсией находится промах.

Следует очистить результаты повторных измерений от промахов, увеличить число повторных измерений, снова определить  и проверить их однородность. Если все дисперсии  и однородны, можно переходить к следующему действию.

3) Вычисляется дисперсия воспроизводимости (S²_воспр). Дисперсия воспроизводимости – это среднее из дисперсий () всех опытов. Дисперсия воспроизводимости характеризует средний разброс результатов повторных измерений во всех опытах относительно своих математических ожиданий.

Если в каждом опыте число повторных измерений одинаково и равно п, то S²_воспр определяется по формуле:

S²_воспр =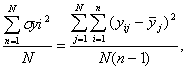

где N – число опытов,  – математическое ожидание в j-м опыте. Если в опытах число повторных измерений различно, то S²_воспр определяется как средневзвешенная величина

S²_воспр =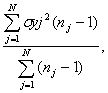

где – число повторных измерений в j–м опыте.

Число степеней свободы дисперсии воспроизводимости равно сумме чисел степеней свободы дисперсий опытов:

.

4) Вычисляется дисперсия адекватности (S²_ад). Дисперсия адекватности – это сумма квадратов отклонений расчётных и экспериментальных значений функции отклика в каждом опыте, отнесённая к числу степеней свободы. Она характеризует разброс экспериментальных результатов относительно расчётных и определяется по формуле:

S²_ад =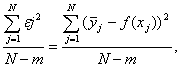

где т – число постоянных коэффициентов в уравнении регрессии;  — математическое ожидание в j–м опыте; N – m = f_ад – число степеней свободы дисперсии адекватности;

3) Проверяется однородность дисперсий адекватности и воспроизводимости. Дисперсии адекватности и воспроизводимости будут однородными, если их отношение будет меньше табличного значения критерия Фишера:

S²_ад / S²_воспр < F,

где значения F берутся (см. табл. 2.3)для числа степеней свободы числителя (дисперсии адекватности) и числа степеней свободы знаменателя (дисперсия воспроизводимости).

Если дисперсии S²_ад и S²_воспр однородны , то с доверительной вероятностью Р = 0,95 можно утверждать, что составленное уравнение регрессии адекватно. Это следует из того, что при и  разброс экспериментальных значений функции отклика относительно её расчётных значений равен среднему разбросу результатов повторных измерений в каждом опыте относительно своих математических ожиданий.

Если S²_ад / S²_воспр > F, то выбранное уравнение регрессии неадекватно. Следует перейти к уравнению регрессии более высокого порядка или выбрать уравнение регрессии другого вида, определить значения коэффициента и снова проверить адекватность.

Если опыты состоят из однократных измерений, то адекватность уравнения регрессии не может быть проверена изложенным способом. В этом случае проверка адекватности уравнения регрессии может быть осуществлена сравнением доверительного интервала функции отклика (а_у) с отклонениями расчётных и экспериментальных значений функции отклика (). Очевидно, что, если < а_у, то уравнение регрессии адекватно.

У_расч.
– значение, рассчитанное по регрессии;

N – число опытов матрицы (равно 8);

К – число
статистически значимых коэффициентов (равно 6);

1 – учитывает
свободный член в уравнении регрессии.

Схема расчета
дисперсии адекватности приведена в таблице 1.4.

Таблица 1.4

Расчет дисперсии
адекватности

Величина

1.2.3. 
Проверка гипотезы адекватности модели по критерию Фишера.

Гипотезу
адекватности проверяем по критерию Фишера. Расчетное значение критерия Фишера
равно:

F табличное при f_з = m – 1 = 3, f_ч = N – K – 1 = 1 и α = 0,05 равно 10,1.

Табличное
значение меньше расчетного, следовательно, модель нельзя признать адекватной.

1.3    Проверка
нормальности распределения данных

           
Для данных таких n₀ = m
= 4, опытов 9-12 , процедура проверки нормальности включает:

1.3.1. Упорядочение
этих данных (75,3; 75,4; 75,5; 75,6) от меньшего к большему

75,3 < 75,4 <
75,5 < 75,6

1.3.2. Вычисление суммы
квадратов отклонений данных от их среднего 

         значения:

    Оценку дисперсии адекватности рассчитывают по формуле  [c.614]

    Дисперсия адекватности определена по формуле [c.302]

    Дисперсия остаточная (дисперсия адекватности — дисперсия, характеризующая рассеивание опытных данных относительно уравнения регрессии. [c.263]

    Уравнение адекватно, если составленное таким образом f-отношение меньше табличного для выбранного уровня значимости р (обычно равного 0,5) и чисел степеней свободы дисперсии адекватности и дисперсии воспроизводимости  [c.185]

    Табличное значение Рт бл рассчитывается в зависимости от числа степеней свободы для максимального и минимального значений оценки дисперсий адекватности и табличной величины доверительного интервала. [c.142]

    Проверка адекватности математической модели. Оценка дисперсии адекватности определялась по формуле (7.1.2.7) 4=0,01165. [c.615]

    С оценкой дисперсии адекватности связано число степеней свободы / = -В. Математическая модель считается адекватной, если выполняется условие [c.610]

    Проверим адекватность этого уравнения эксперименту по критерию Фишера. Дисперсия адекватности определяется по (У.38)  [c.176]

    Дисперсия адекватности модели характеризует меру отклонения данных у, (рнс 61), рассчитанных по уравнению регрессии, от экспериментальных результатов у, для -аст точки, в которой проведено измерение [c.494]

    Дисперсия адекватности — числитель критерия Фи- [c.87]

    Здесь дисперсия регрессии з1 вычисляется по формуле (4.31), а дисперсия адекватности—по формуле [c.107]

    Прежде чем найти его значение по имеющимся выборкам, вычислим значения дисперсий адекватности и воспроизводимости  [c.54]

    Понятно, что оценка целевой функции у улучшается при ее повторных измерениях. Длительность исследований возрастает, но это не сказывается на выполнении производственной программы. Особое значение имеют при этом оценки погрешности измерения величины г/, расчета величин 6, и их дисперсий адекватности уравнения регрессии. Все расчеты проводятся на основе приведенных выше (с. 24—26) соотношении. [c.42]

    Сравнение дисперсии адекватности  [c.101]

    Расчетное значение критерия Фишера формируют как отношение дисперсии адекватности к дисперсии опыта [c.235]

    Следовательно, расчетное значение критерия Фишера (формула (7.1.2.6)) будет р = 3,416, а число степеней свободы, связанное с оценкой дисперсии адекватности, составит Уад = 2. Табличное значение критерия Фишера (см. табл. 7.1.2.3), соответствующее числу степеней свободы числителя 8 и числу степеней свободы знаменателя 2 при а = 0,05, равно Р 19,3. Поскольку Р> Fp, то, согласно условию (7.1.2.8), найденную математическую модель следует признать адекватной. [c.615]

    Суммы квадратов, обусловленные различными источниками, будучи поделенными на соответствующие числа степеней свободы, определяют соответствующие дисперсии. Очевидно, что адекватность модели может определяться отношением дисперсии адекватности модели к дисперсии воспроизводимости (/ -статистика). Если это отношение велико (по крайней мере существенно больше единицы), то имеются достаточно веские доводы в пользу того, что испытываемая модель не отражает результаты эксперимента. [c.44]

    Число степеней свободы дисперсии адекватности составляет /ад= -Р/. (2.97) [c.45]

    По имеющимся экспериментальным данным дисперсию воспроизводимости оценить невозможно. Поэтому с помощью критерия Фишера оценим целесообразность использования ячеечной модели, сравнив дисперсию относительно среднего 5 “р с дисперсией адекватности [c.111]

    Найдем дисперсию адекватности  [c.111]

    Уравнение адекватно, есл1 Г<Р -ра, /з), где — число степеней свободы дисперсии адекватности /г — число степеней свободы дчсперсип воспроизводимости. [c.196]

    Коэффициенты уравнения регрессии значимы, если й(0, ц, [ ) >йв-Уравнение адекватно, если Рр<Рт. 5 — дисперсия поспроизводимости эксперимента 2 —дисперсия адекватности — доверительный интервал. [c.61]

    Результаты экспериментов обрабатывали на ЭВМ Искра-1256 с точностью 10 и конечные результаты выводили на печатаюшее устройство в виде значений констант скорости, коэффициента корреляции, дисперсии адекватности и постоянных А и В уравнения регрессии [c.87]

    Полученное уравнение регрессии проверяют на адекватность с помощью критерия Фишера. Для этого сначала по уравнению регрессии (15.6) рассчитывают величину оптической плотности у расч И ПО формуле (15.7) определяют дисперсию адекватности [c.153]

    Экспериментально показана эффективность применения данной модели для описания процесса биологической очистки [11]. Так, сравнительная статистическая оценка моделей Герберта (I), Иерусалимского (II) и Кенела (III) составила дисперсия адекватности— 1—0,12 11 — 0,091 111 —0,055 разброс значений коэффициентов — I — 14—31 % 11 — 8—22% III — 0,7—1,8,7о Дальнейшим развитием этого направления являются модели трехфазного биоценоза, модели типа хищник — жертва [19]. [c.226]

    Оценим целесообразность использования ячеечной модел для описания движения потока жидкости на ректификационной тарелке, сравнив дисперсию относительно среднего 5ср и дисперсию адекватности 5ад. Для этого составим ютношение в виде [c.55]

Аналитическая химия Часть 2 (1989) — [

c.371

]

Теория технологических процессов основного органического и нефтехимического синтеза (1975) — [

c.260

]

Теория химических процессов основного органического и нефтехимического синтеза Издание 2 (1984) — [

c.89

]

Регенерация адсорбентов (1983) — [

c.137

,

c.138

]