Как найти дисперсию через среднее арифметическое

Как найти дисперсию?

Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.

Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.

Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.

Другие задачи с решениями по ТВ

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку “Вычислить”.
• Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.

Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом  (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

• Определите среднее (простое среднее арифметическое ряда значений).
• Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
• Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее   мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

   

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки =  мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

.

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

.

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

.

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

.

Для второго примера получится:

.

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения.

Основными обобщающими
показателями вариации в статистике
являются дисперсии и среднее квадратическое
отклонение.

Дисперсия
– это средняя арифметическая квадратов
отклонений каждого значения признака
от общей средней. Дисперсия обычно
называется средним квадратом отклонений
и обозначается
.
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:

—дисперсия
невзвешенная (простая);

—дисперсия
взвешенная.

Среднее квадратическое
отклонение представляет собой корень
квадратный из дисперсии и обозначается
S:

—среднее
квадратическое отклонение невзвешенное;

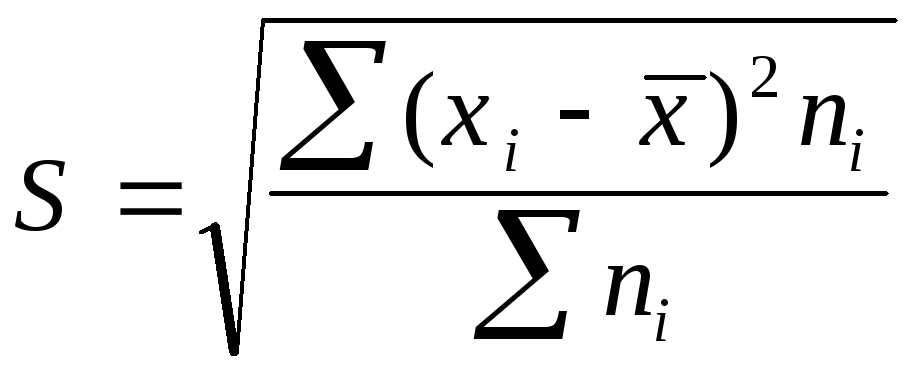—среднее
квадратическое отклонение взвешенное.

Среднее
квадратическое отклонение
– это обобщающая характеристика абсолютных
размеров вариации признака в совокупности.
Выражается оно в тех же единицах
измерения, что и признак (в метрах,
тоннах, процентах, гектарах и т.д.).

Среднее квадратическое
отклонение является мерилом надежности
средней. Чем меньше среднее квадратическое
отклонение, тем лучше средняя арифметическая
отражает собой всю представляемую
совокупность.

Вычислению среднего
квадратического отклонения предшествует
расчет дисперсии.

Порядок расчета
дисперсии взвешенную:

1) определяют
среднюю арифметическую взвешенную

;

2) определяются
отклонения вариант от средней
;

3) возводят в квадрат
отклонение каждой варианты от средней
;

4) умножают квадраты
отклонений на веса (частоты)
;

5) суммируют
полученные произведения

;

6) Полученную сумму
делят на сумму весов

.

Пример 3.

Таблица 6.3.

Произведено продукции одним рабочим, шт. (варианта)	Число рабочих,
8	7	56	-2	4	28
9	10	90	-1	1	10
10	15	150	0	0	0
11	12	132	1	1	12
12	6	72	2	4	24
ИТОГО	50	500			74

Исчислим среднюю
арифметическую взвешенную:

шт.

Значения отклонений
от средней и их квадратов представлены
в таблице 6.3. Определим дисперсию:

=1,48

Среднее квадратическое
отклонение будет равно:

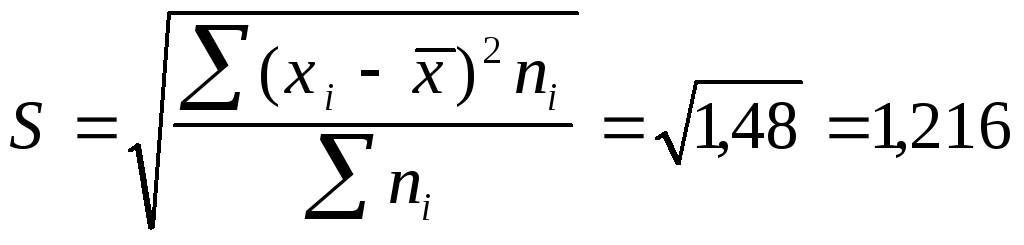шт.

Если исходные
данные представлены в виде интервального
ряда распределения, то сначала надо
определить дискретное значение признака,
а далее применить тот же метод, что
изложен выше.

Пример 4.

Покажем расчет
дисперсии для интервального ряда на
данных о распределении посевной площади
колхоза по урожайности пшеницы:

Таблица 6.4

Урожайность пшеницы, ц/га	Посевная площадь, га
14 – 16	100	15	1500	-3,4	11,56	1156
16 – 18	300	17	5100	-1,4	1,96	588
18 – 20	400	19	7600	0,6	0,36	144
20 – 22	200	21	4200	2,6	6,76	1352
ИТОГО	1000		18400			3240

Средняя арифметическая
равна:

ц с 1га.

Исчислим дисперсию:

Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.

Техника вычисления
дисперсии сложна, а при больших значениях
вариант и частот может быть громоздкой.
Расчеты можно упростить, используя
свойства дисперсии.

Свойства
дисперсии.

1. Уменьшение или
   увеличение весов (частот) варьирующего
   признака в определенное число раз
   дисперсии не изменяет.

2. Уменьшение или
   увеличение каждого значения признака
   на одну и ту же постоянную величину А
   дисперсии не изменяет.

3. Уменьшение или
   увеличение каждого значения признака
   в какое-то число раз к соответственно
   уменьшает или увеличивает дисперсию
   в
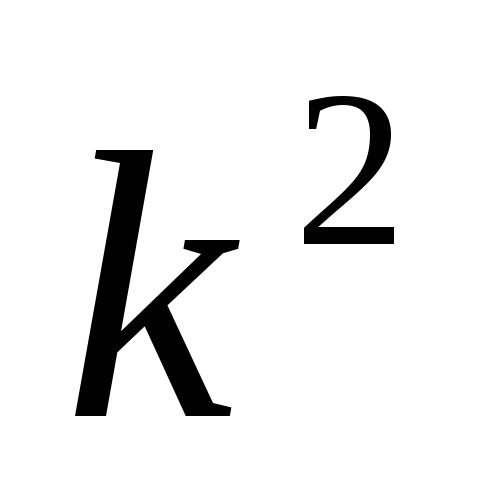   раз, а среднее квадратическое отклонение
   – в к раз.

4. Дисперсия признака
   относительно произвольной величины
   всегда больше дисперсии относительно
   средней арифметической на квадрат
   разности между средней и произвольной
   величиной:
   .
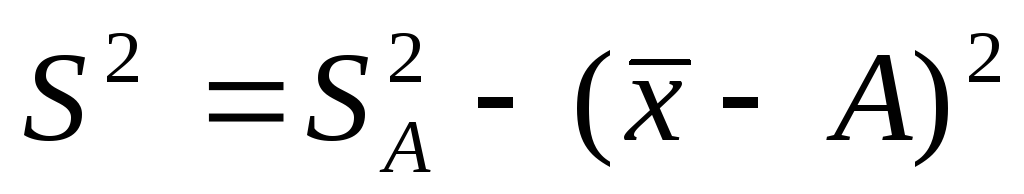   Если А равна нулю, то приходим к
   следующему равенству:,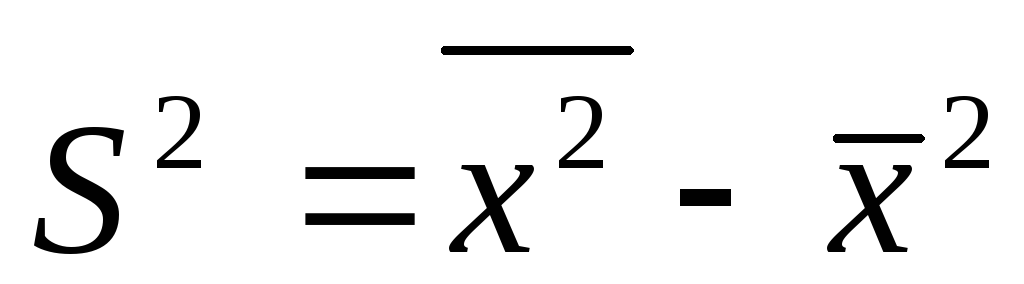
   т.е. дисперсия признака равна разности
   между средним квадратом значений
   признака и квадратом средней.

Каждое свойство
при расчете дисперсии может быть
применено самостоятельно или в сочетании
с другими.

Порядок расчета
дисперсии простой:

1) определяют
среднюю арифметическую
;

2) возводят в квадрат
среднюю арифметическую;

3) возводят в квадрат
каждую варианту ряда
;

4) находим сумму
квадратов вариант
;

5) делят сумму
квадратов вариант на их число, т.е.
определяют средний квадрат
;

6) определяют
разность между средним квадратом
признака и квадратом средней
.

Пример 5.

Имеются следующие
данные о производительности труда
рабочих:

Таблица
6.4

Табельный номер рабочего	Произведено продукции, шт.
1	8	64
2	9	81
3	10	100
4	11	121
5	12	144
ИТОГО	50	510

Произведем следующие
расчеты:

шт.

Пример 6.

Определить дисперсию
в дискретном ряду распределения,
используя табл. 6.5.

Таблица 6.5.

Произведено продукции 1 рабочим, шт. (х)	Число рабочих, n
8	7	56	64	448
9	10	90	81	810
10	15	150	100	1500
11	12	132	121	1452
12	6	72	144	864
ИТОГО	50	500	510	5074

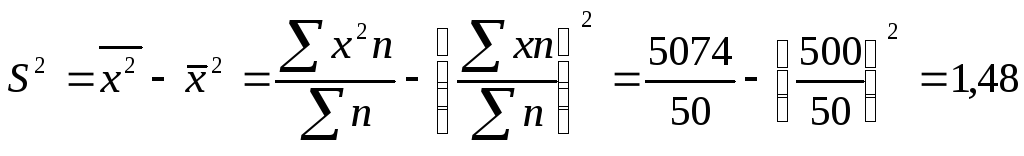
Получим тот же
результат, что в табл. 6.3.

Рассмотрим расчет
дисперсии в интервальном ряду
распределения.

Порядок расчета
дисперсии взвешенной (по формуле
):

1. определяют среднюю
   арифметическую
   ;

2. возводят в квадрат
   полученную среднюю
   ;

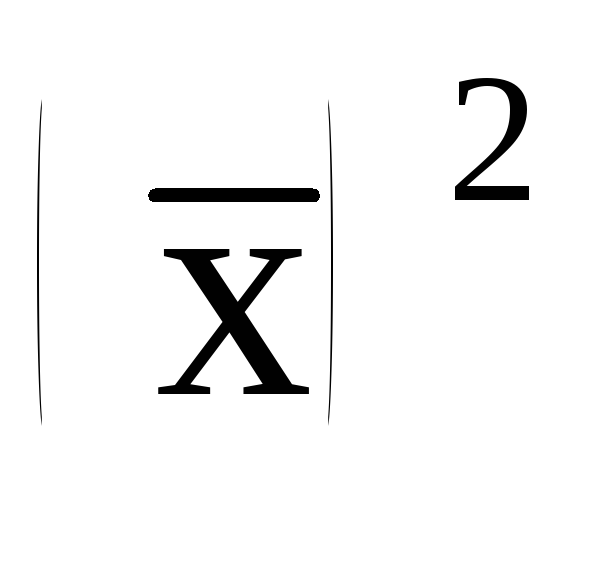3. возводят в квадрат
   каждую варианту ряда
   ;

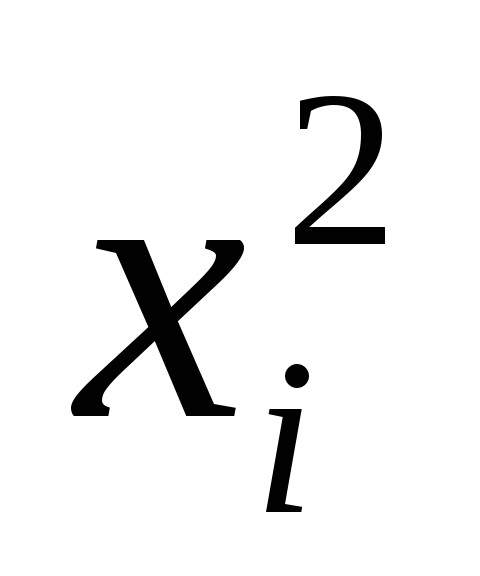4. умножают квадраты
   вариант на частоты
   ;

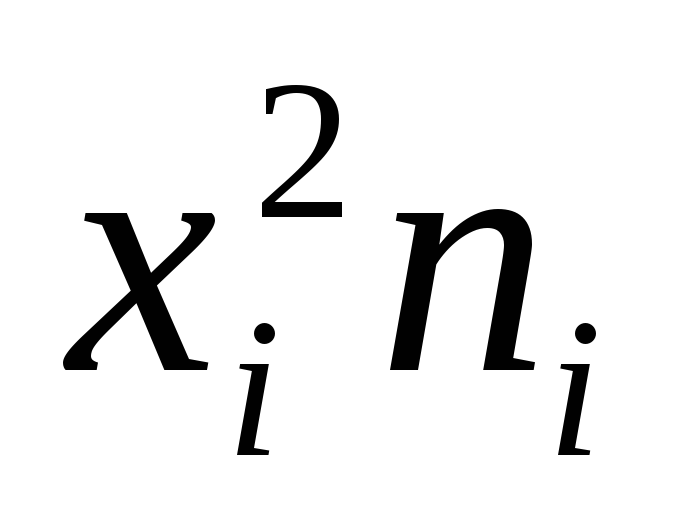5. суммируют полученные
   произведения
   ;

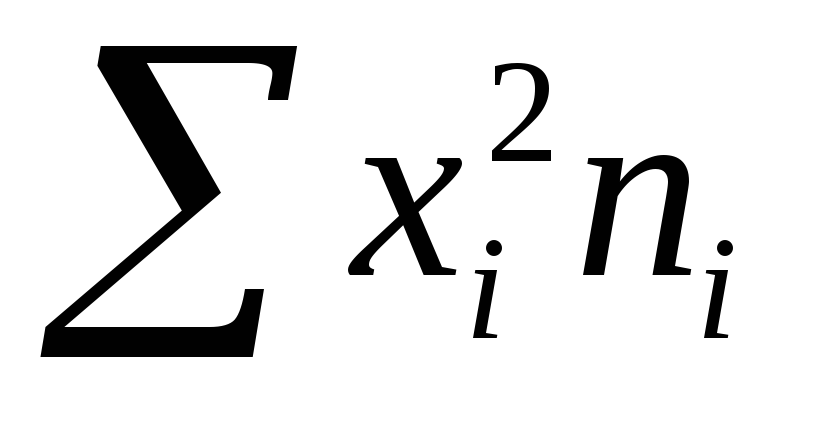6. делят полученную
   сумму на сумму весов и получают средний
   квадрат признака
   ;

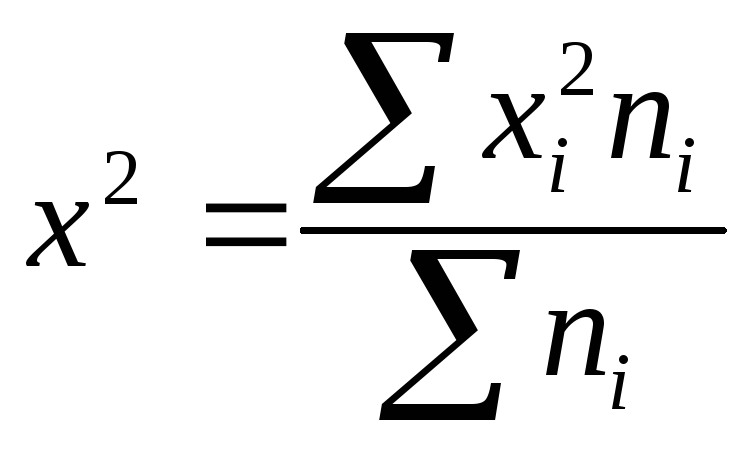7. определяют разность
   между средним значением квадратов и
   квадратом средней арифметической, т.е.
   дисперсию
   .

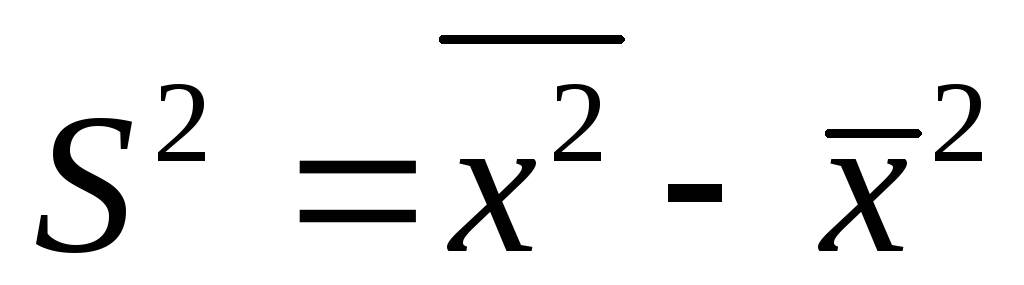Пример 7.

Имеются следующие
данные о распределении посевной площади
колхоза по урожайности пшеницы:

Таблица 6.6

Урожайность пшеницы, ц/га	Посевная площадь, га
14 – 16	100	15	1500	225	22500
16 – 18	300	17	5100	289	36700
18 – 20	400	19	7600	361	144400
20 – 22	200	21	4200	441	88200
ИТОГО	1000		18400		341200

В подобных примерах
прежде всего определяется дискретное
значение признака в каждом интервале,
а затем применяется метод расчета,
указанный выше:

Средняя величина
отражает тенденцию развития, т.е.
действие главных причин. Среднее
квадратическое отклонение измеряет
силу воздействия прочих факторов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

On-line калькулятор, который выполняет расчеты среднего арифметического показателя, Дисперсии, Вариации, Среднеквадратичного отклонения, удобный в использовании. Для получения правильного результата необходимо правильно заполнить предложенную таблицу.

Такой онлайн калькулятор станет незаменимым помощником для осуществления математических расчетов. Указав нужные значения вам достаточно нажать кнопку “Расчет” и незамедлительно появится правильный результат. Простота в использовании делает калькулятор незаменимым и популярным. Им легко пользоваться на работе, дома, во время учебы. Он не требует выполнения сложных действий. Вы сможете сделать все вычисления для всех нужных величин.