Как найти дисперсию матлаб - Сайт, где вы сможете решить свои вопросы

Syntax

Description

example

V = var(A) returns the variance
of the elements of A along the first array dimension whose size
is greater than 1. By default, the variance is normalized by N-1,
where N is the number of observations.

If A is a vector of observations, then
V is a scalar.
If A is a matrix whose columns are random variables and
whose rows are observations, then V is a row vector
containing the variance corresponding to each column.
If A is a multidimensional array, then
var(A) operates along the first array dimension whose
size is greater than 1, treating the elements as vectors. The size of
V in this dimension becomes 1,
while the sizes of all other dimensions are the same as in
A.
If A is a scalar, then V is
0.
If A is a 0-by-0
empty array, then V is NaN.
If A is a table
or timetable, then var(A) returns a one-row table
containing the variance of each variable. (since R2023a)

example

V = var(A,w)
specifies a weighting scheme. When w = 0 (default), the variance
is normalized by N-1, where N is the number of
observations. When w = 1, the variance is normalized by the
number of observations. w can also be a weight vector containing
nonnegative elements. In this case, the length of w must equal
the length of the dimension over which var is operating.

V = var(A,w,"all")
returns the variance over all elements of A when
w is either 0 or 1.

example

V = var(A,w,dim)
returns the variance along dimension dim. To maintain the default
normalization while specifying the dimension of operation, set w = 0 in the second argument.

example

V = var(A,w,vecdim)
returns the variance over the dimensions specified in the vector
vecdim when w is 0 or 1. For example, if
A is a matrix, then var(A,0,[1 2]) returns
the variance over all elements in A because every element of a
matrix is contained in the array slice defined by dimensions 1 and 2.

example

V = var(___,nanflag)
specifies whether to include or omit NaN values in
A for any of the previous syntaxes. For example,
var(A,"omitnan") ignores NaN values when
computing the variance. By default, var includes
NaN values.

Examples

collapse all

Variance of Matrix

Create a matrix and compute its variance.

A = [4 -7 3; 1 4 -2; 10 7 9];
var(A)

ans = 1×3

   21.0000   54.3333   30.3333

Variance of Array

Create a 3-D array and compute its variance.

A(:,:,1) = [1 3; 8 4];
A(:,:,2) = [3 -4; 1 2];
var(A)

ans = 
ans(:,:,1) =

   24.5000    0.5000


ans(:,:,2) =

     2    18

Specify Variance Weight Vector

Create a matrix and compute its variance according to a weight vector w.

A = [5 -4 6; 2 3 9; -1 1 2];
w = [0.5 0.25 0.25];
var(A,w)

ans = 1×3

    6.1875    9.5000    6.1875

Specify Dimension for Variance

Create a matrix and compute its variance along the first dimension.

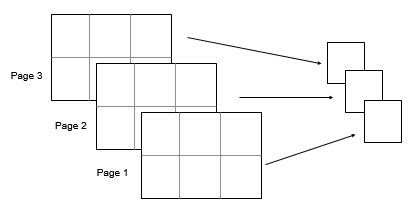
A = [4 -2 1; 9 5 7];
var(A,0,1)

ans = 1×3

   12.5000   24.5000   18.0000

Compute the variance of A along the second dimension.

Variance of Array Page

Create a 3-D array and compute the variance over each page of data (rows and columns).

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
V = var(A,0,[1 2])

V = 
V(:,:,1) =

    6.2500


V(:,:,2) =

    60


V(:,:,3) =

   20.9167

Variance Excluding Missing Values

Create a matrix containing NaN values.

A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]

A = 2×4

    1.7700   -0.0050       NaN   -2.9500
       NaN    0.3400       NaN    0.1900

Compute the variance of the matrix, excluding NaN values. For matrix columns that contain any NaN value, var computes with non-NaN elements. For matrix columns that contain all NaN values, the variance is NaN.

V = 1×4

         0    0.0595       NaN    4.9298

Variance and Mean

Create a matrix and compute the variance and mean of each column.

A = [4 -7 3; 1 4 -2; 10 7 9];
[V,M] = var(A)

V = 1×3

   21.0000   54.3333   30.3333

M = 1×3

    5.0000    1.3333    3.3333

Create a matrix and compute the weighted variance and weighted mean of each column according to a weight vector w.

A = [5 -4 6; 2 3 9; -1 1 2];
w = [0.5 0.25 0.25];
[V,M] = var(A,w)

V = 1×3

    6.1875    9.5000    6.1875

M = 1×3

    2.7500   -1.0000    5.7500

Input Arguments

collapse all

`A` — Input array
vector | matrix | multidimensional array | table | timetable

Input array, specified as a vector, matrix, multidimensional array, table, or timetable. If
A is a scalar, then var(A) returns
0. If A is a
0-by-0 empty array, then
var(A) returns NaN.

Data Types: single | double | table | timetable
Complex Number Support: Yes

`w` — Weight
`0` (default) | `1` | vector

Weight, specified as one of:

0 — Normalize by
N-1, where N is the
number of observations. If there is only one observation, then
the weight is 1.
1 — Normalize by
N.
Vector made up of nonnegative scalar weights corresponding to
the dimension of A along which the variance
is calculated.

Data Types: single | double

`dim` — Dimension to operate along
positive integer scalar

Dimension
to operate along, specified as a positive integer scalar. If you do not specify the dimension,
then the default is the first array dimension of size greater than 1.

Dimension dim indicates the dimension whose
length reduces to 1. The size(V,dim) is 1,
while the sizes of all other dimensions remain the same.

Consider an m-by-n input matrix,
A:

var(A,0,1) computes the variance of the
elements in each column of A and returns a
1-by-n row
vector.
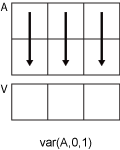
var(A,0,2) computes the variance of the
elements in each row of A and returns an
m-by-1 column
vector.

If dim is greater than ndims(A),
then var(A) returns an array of zeros the same size as
A.

`vecdim` — Vector of dimensions
vector of positive integers

Vector of dimensions, specified as a vector of positive integers. Each
element represents a dimension of the input array. The lengths of the output
in the specified operating dimensions are 1, while the others remain the
same.

Consider a 2-by-3-by-3 input array, A. Then
var(A,0,[1 2]) returns a 1-by-1-by-3 array whose
elements are the variances computed over each page of
A.

`nanflag` — Missing value condition
`"includemissing"` (default) | `"includenan"` | `"omitmissing"` | `"omitnan"`

Missing value condition, specified as one of these values:

"includemissing" or
"includenan" — Include
NaN values in A when
computing the variance. If any element in the operating dimension is
NaN, then the corresponding element in
V is NaN.
"includemissing" and
"includenan" have the same behavior.
"omitmissing" or "omitnan"
— Ignore NaN values in
A and w, and compute the
variance over fewer points. If all elements in the operating
dimension are NaN, then the corresponding element
in V is NaN.
"omitmissing" and
"omitnan" have the same behavior.

Output Arguments

collapse all

`V` — Variance
scalar | vector | matrix | multidimensional array | table

Variance, returned as a scalar, vector, matrix, multidimensional array, or table.

If A is a vector of observations, then
V is a scalar.
If A is a matrix whose columns are random
variables and whose rows are observations, then
V is a row vector containing the variance
corresponding to each column.
If A is a multidimensional array, then
var(A) operates along the first array
dimension whose size is greater than 1, treating the elements as
vectors. The size of V in this dimension
becomes 1, while the sizes of all other
dimensions are the same as in A.
If A is a scalar, then V
is 0.
If A is a
0-by-0 empty array,
then V is NaN.
If A
is a table or timetable, then V is a one-row
table. If the variables of A have units, then
the variables of V do not have those
units. (since R2023a)

`M` — Mean
scalar | vector | matrix | multidimensional array | table

Mean, returned as a scalar, vector, matrix, multidimensional array, or table.

If A is a vector of observations, then
M is a scalar.
If A is a matrix whose columns are random
variables and whose rows are observations, then
M is a row vector containing the mean
corresponding to each column.
If A is a multidimensional array, then
var(A) operates along the first array
dimension whose size is greater than 1, treating the elements as
vectors. The size of M in this dimension
becomes 1, while the sizes of all other
dimensions are the same as in A.
If A is a scalar, then M
is equal to A.
If A is a
0-by-0 empty array,
then M is NaN.
If A
is a table or timetable, then M is a one-row
table. If the variables of A have units, then
the variables of M have the same
units. (since R2023a)

If V is the weighted variance, then
M is the weighted mean.

More About

collapse all

Variance

For a random variable vector A made up of
N scalar observations, the variance is defined as

where μ is the mean of A,

Some definitions of variance use a normalization factor
N instead of N – 1. You can use a
normalization factor of N by specifying a weight of
1, producing the second moment of the sample about its
mean.

Regardless of the normalization factor for the variance, the mean
is assumed to have the normalization factor N.

Weighted Variance

For a finite-length vector A made up of
N scalar observations and weighting scheme
w, the weighted variance is defined as

where μ_w is the weighted
mean of A.

Weighted Mean

For a finite-length vector A made up of
N scalar observations and weighting scheme
w, the weighted mean is defined as

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

This function supports tall arrays with the limitation:

The weighting scheme cannot be a vector.

For more information, see Tall Arrays for Out-of-Memory Data.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

C++ code generation supports the following syntaxes:
- V = var(A)
- V = var(A,w)
- V = var(A,w,"all")
- V = var(A,w,dim)
- V = var(A,w,vecdim)
- V = var(__,nanflag)
When specified, dimension must be a constant.
See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

If specified, dim must be a constant.
GPU code generation supports the following syntaxes:
- V = var(A)
- V = var(A,w)
- V = var(A,w,"all")
- V = var(A,w,dim)
- V = var(A,w,vecdim)
- V = var(__,nanflag)

Thread-Based Environment
Run code in the background using MATLAB® `backgroundPool` or accelerate code with Parallel Computing Toolbox™ `ThreadPool`.

This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a

expand all

R2023a: Perform calculations directly on tables and timetables

The var function can calculate on all variables within a table or
timetable without indexing to access those variables. All variables must have data types
that support the calculation. For more information, see Direct Calculations on Tables and Timetables.

R2023a: Specify missing value condition

Include or omit missing values in the input arrays when computing the variance by
using the "includemissing" or "omitmissing"
options. These options have the same behavior as the "includenan"
and "omitnan" options, respectively.

R2023a: Improved performance with small group size

The var function shows improved performance when computing
over a real vector when the operating dimension is not specified. The function
determines the default operating dimension more quickly in R2023a than in
R2022b.

For example, this code computes the variance along the default vector dimension.
The code is about 1.6x faster than in the previous release.

function timingVar
A = rand(10,1);
for i = 1:8e5
    var(A);
end
end

The approximate execution times are:

R2022b: 1.29 s

R2023a: 0.79 s

The code was timed on a Windows^® 10, Intel^®
Xeon^® CPU E5-1650 v4 @ 3.60 GHz test system using the
timeit function.

R2022a: Return mean or weighted mean

The var function can now return the mean of the input elements
used to calculate the variance by using a second output argument
M. If a weighting scheme is specified, then
var returns the weighted
mean.

R2018b: Operate on multiple dimensions

Operate on multiple dimensions of the input array at a time. Specify a vector of
operating dimensions, or specify the "all" option to operate on
all array dimensions.

Источник

Variance of probability distribution

Syntax

Description

example

v = var(pd) returns
the variance v of the probability distribution
pd.

Examples

collapse all

Variance of a Fitted Distribution

Load the sample data. Create a vector containing the first column of students’ exam grade data.

load examgrades
x = grades(:,1);

Fit a normal distribution object to the data.

pd = 
  NormalDistribution

  Normal distribution
       mu = 75.0083   [73.4321, 76.5846]
    sigma =  8.7202   [7.7391, 9.98843]

Compute the variance of the fitted distribution.

For a normal distribution, the variance is equal to the square of the parameter sigma.

Variance of Skewed Distribution

Create a Weibull probability distribution object.

pd = makedist('Weibull','A',5,'B',2)

pd = 
  WeibullDistribution

  Weibull distribution
    A = 5
    B = 2

Compute the variance of the distribution.

Variance of Triangular Distribution

Create a triangular distribution object.

pd = makedist('Triangular','A',-3,'B',1,'C',3)

pd = 
  TriangularDistribution

A = -3, B = 1, C = 3

Compute the variance of the distribution.

Variance of a Kernel Distribution

Load the sample data. Create a vector containing the first column of students’ exam grade data.

load examgrades;
x = grades(:,1);

Fit a kernel distribution object to the data.

pd = 
  KernelDistribution

    Kernel = normal
    Bandwidth = 3.61677
    Support = unbounded

Compute the variance of the fitted distribution.

Input Arguments

collapse all

Probability distribution, specified as one of the probability distribution objects in
the following table.

Distribution Object	Function or App Used to Create Probability Distribution Object
`BetaDistribution`	`makedist`, `fitdist`, Distribution Fitter
`BinomialDistribution`	`makedist`, `fitdist`, Distribution Fitter
`BirnbaumSaundersDistribution`	`makedist`, `fitdist`, Distribution Fitter
`BurrDistribution`	`makedist`, `fitdist`, Distribution Fitter
`ExponentialDistribution`	`makedist`, `fitdist`, Distribution Fitter
`ExtremeValueDistribution`	`makedist`, `fitdist`, Distribution Fitter
`GammaDistribution`	`makedist`, `fitdist`, Distribution Fitter
`GeneralizedExtremeValueDistribution`	`makedist`, `fitdist`, Distribution Fitter
`GeneralizedParetoDistribution`	`makedist`, `fitdist`, Distribution Fitter
`HalfNormalDistribution`	`makedist`, `fitdist`, Distribution Fitter
`InverseGaussianDistribution`	`makedist`, `fitdist`, Distribution Fitter
`KernelDistribution`	`fitdist`, Distribution Fitter
`LogisticDistribution`	`makedist`, `fitdist`, Distribution Fitter
`LoglogisticDistribution`	`makedist`, `fitdist`, Distribution Fitter
`LognormalDistribution`	`makedist`, `fitdist`, Distribution Fitter
`LoguniformDistribution`	`makedist`
`MultinomialDistribution`	`makedist`
`NakagamiDistribution`	`makedist`, `fitdist`, Distribution Fitter
`NegativeBinomialDistribution`	`makedist`, `fitdist`, Distribution Fitter
`NormalDistribution`	`makedist`, `fitdist`, Distribution Fitter
`PiecewiseLinearDistribution`	`makedist`
`PoissonDistribution`	`makedist`, `fitdist`, Distribution Fitter
`RayleighDistribution`	`makedist`, `fitdist`, Distribution Fitter
`RicianDistribution`	`makedist`, `fitdist`, Distribution Fitter
`StableDistribution`	`makedist`, `fitdist`, Distribution Fitter
`tLocationScaleDistribution`	`makedist`, `fitdist`, Distribution Fitter
`TriangularDistribution`	`makedist`
`UniformDistribution`	`makedist`
`WeibullDistribution`	`makedist`, `fitdist`, Distribution Fitter

Output Arguments

collapse all

`v` — Variance
nonnegative scalar value

Variance of the probability distribution, returned as a nonnegative scalar
value.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

The input argument pd can be a fitted
probability distribution object for beta, exponential, extreme value, lognormal, normal, and
Weibull distributions. Create pd by fitting a probability distribution to
sample data from the fitdist function. For an example, see Code Generation for Probability Distribution Objects.

For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more
information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2013a

Источник

Синтаксис

Описание

пример

V = var(A) возвращает дисперсию элементов A вдоль первого измерения массива, размер которого не равняется 1.

Если A вектор из наблюдений, отклонение является скаляром.
Если A матрица, столбцы которой являются случайными переменными и чьи строки являются наблюдениями, V вектор-строка, содержащий отклонения, соответствующие каждому столбцу.
Если A многомерный массив, затем var(A) обрабатывает значения вдоль первого измерения массива, размер которого не равняется 1 как векторы. Размер этой размерности становится 1 в то время как размеры всех других размерностей остаются то же самое.
Отклонение нормировано на количество observations-1 по умолчанию.
Если A скаляр, var(A) возвращает 0. Если A 0– 0 пустой массив, var(A) возвращает NaN.

пример

V = var(A,w) задает схему взвешивания. Когда w = 0 (значение по умолчанию), V нормирован на количество observations-1. Когда w = 1, это нормировано на количество наблюдений. w может также быть вектор веса, содержащий неотрицательные элементы. В этом случае, длина w должен равняться длине размерности по который var действует.

V = var(A,w,'all') вычисляет изменение по всем элементам A когда w или 0 или 1. Этот синтаксис допустим для MATLAB^® версии R2018b и позже.

пример

V = var(A,w,dim) возвращает дисперсию по измерению dim. Чтобы обеспечить нормализацию по умолчанию при определении размерности операции, установите w = 0 во втором аргументе.

пример

V = var(A,w,vecdim) вычисляет отклонение по размерностям, заданным в векторном vecdim когда w 0 или 1. Например, если A матрица, затем var(A,0,[1 2]) вычисляет отклонение по всем элементам в A, поскольку каждый элемент матрицы содержится в срезе массивов, заданном размерностями 1 и 2.

пример

V = var(___,nanflag) задает, включать ли или не использовать NaN значения от вычисления для любого из предыдущих синтаксисов. Например, var(A,'includenan') включает весь NaN значения в A в то время как var(A,'omitnan') игнорирует их.

Примеры

свернуть все

Отклонение матрицы

Создайте матрицу и вычислите ее отклонение.

A = [4 -7 3; 1 4 -2; 10 7 9];
var(A)

ans = 1×3

   21.0000   54.3333   30.3333

Отклонение массива

Создайте трехмерный массив и вычислите его отклонение.

A(:,:,1) = [1 3; 8 4];
A(:,:,2) = [3 -4; 1 2];
var(A)

ans = 
ans(:,:,1) =

   24.5000    0.5000


ans(:,:,2) =

     2    18

Определение вектора веса отклонения

Создайте матрицу и вычислите ее отклонение согласно вектору веса w.

A = [5 -4 6; 2 3 9; -1 1 2];
w = [0.5 0.25 0.25];
var(A,w)

ans = 1×3

    6.1875    9.5000    6.1875

Определение размерности для отклонения

Создайте матрицу и вычислите ее отклонение по первому измерению.

A = [4 -2 1; 9 5 7];
var(A,0,1)

ans = 1×3

   12.5000   24.5000   18.0000

Вычислите отклонение A вдоль второго измерения.

Отклонение страницы массивов

Создайте трехмерный массив и вычислите отклонение по каждой странице данных (строки и столбцы).

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
V = var(A,0,[1 2])

V = 
V(:,:,1) =

    6.2500


V(:,:,2) =

    60


V(:,:,3) =

   20.9167

`Отклонение, исключая NaN`

Создайте вектор и вычислите его отклонение, исключая NaN значения.

A = [1.77 -0.005 3.98 -2.95 NaN 0.34 NaN 0.19];
V = var(A,'omitnan')

Входные параметры

свернуть все

`A` — Входной массив
вектор | матрица | многомерный массив

Входной массив, заданный как векторный, матричный или многомерный массив.

Типы данных: single | double
Поддержка комплексного числа: Да

`w` — Вес
0 (значение по умолчанию) | `1` | вектор

Вес в виде одного из:

0 — нормирует на количество observations-1. Если существует только одно наблюдение, вес равняется 1.
1 — нормирует на количество наблюдений.
вектор, составленный из неотрицательных скалярных весов, соответствующих размерности A вдоль которого вычисляется отклонение.

Типы данных: single | double

`dim` — Размерность, которая задает направление расчета
положительный целочисленный скаляр

Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.

Размерность dim указывает на размерность, длина которой уменьшает до 1. size(V,dim) 1, в то время как размеры всех других размерностей остаются то же самое.

Рассмотрите двумерный входной массив, A.

Если dim = 1, затем var(A,0,1) возвращает вектор-строку, содержащий отклонение элементов в каждом столбце.
Если dim = 2, затем var(A,0,2) возвращает вектор-столбец, содержащий отклонение элементов в каждой строке.

var возвращает массив нулей тот же размер как A когда dim больше ndims(A).

`vecdim` — Вектор из размерностей
вектор из положительных целых чисел

Вектор из размерностей в виде вектора из положительных целых чисел. Каждый элемент представляет размерность входного массива. Продолжительности выхода в заданных операционных размерностях равняются 1, в то время как другие остаются то же самое.

Рассмотрите 2 3х3 входным массивом, A. Затем var(A,0,[1 2]) возвращает 1 1 3 массивами, элементами которых являются отклонения, вычисленные по каждой странице A.

`nanflag` `NaN` условие
`'includenan'` (значение по умолчанию) | `'omitnan'`

NaN условие в виде одного из этих значений:

'includenan' — отклонение входа, содержащего NaN значениями является также NaN.
'omitnan' — весь NaN значения, появляющиеся или во входном массиве или в векторе веса, проигнорированы.

Типы данных: char

Больше о

свернуть все

Дисперсия

Для вектора случайной переменной A составил из скалярных наблюдений N, отклонение задано как

где μ является средним значением A,

Некоторые определения отклонения используют коэффициент нормализации N вместо N-1, который может быть задан установкой w к 1. В любом случае среднее значение принято, чтобы иметь обычный коэффициент нормализации N.

Расширенные возможности

“Высокие” массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Эта функция поддерживает высокие массивы с ограничением:

Схема взвешивания не может быть вектором.

Для получения дополнительной информации смотрите Длинные массивы для Данных, которые не помещаются в память.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Указания и ограничения по применению:

Если задано, dim должна быть константа.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).

Представлено до R2006a

Источник

0 / 0 / 0

Регистрация: 13.05.2013

Сообщений: 20

Дисперсия и мат.ожидание в матрице

23.05.2016, 22:55. Показов 14207. Ответов 7

Дана произвольная матрица (пусть 10х10). Необходимо найти мат. ожидание и дисперсию в каждой строке и каждом столбце.

Вот, что у меня получилось (дисперсию по строкам не нашел):
A=rand(10,10);
B=maen(A); (мат.ожидание в столбце)
C=mean(A,2); (мат.ожидание в строке)
D=var(A); (дисперсия по столбцам)

И еще 1 вопрос при использовании функции var мы получаем G (сигма) или G^2(сигма в квадрате)

Matasin

23.05.2016, 23:07

Не по теме:

Торможу чего-то…:wall:

Модератор

1573 / 1443 / 467

Регистрация: 13.09.2015

Сообщений: 4,961

24.05.2016, 06:29

Тема79, с дисперсией надо поаккуратнее. По какой формуле вы её рассчитываете? Полагаю, вам надо применить следующие команды:
Dc=var(A,1,1); % дисперсия по столбцам
Dr=var(A,1,2); % дисперсия по строкам

0 / 0 / 0

Регистрация: 13.05.2013

Сообщений: 20

24.05.2016, 17:48

[ТС]

Не так. Если использовать эти команды, то получаются слишком большие числа. Так быть не должно.

Norwall

177 / 143 / 50

Регистрация: 07.02.2014

Сообщений: 489

24.05.2016, 17:56

Тема79,

Matlab M

clc, clear all
 
A = rand(10,10);
 
for i = 1:size(A,2)
    B(i,:) = mean(A(i,:)); %мат.ожидание в строках
    C(i,:) = var(A(i,:)); %дисперсия в строках
    D(i,:) = mean(A(:,i)); %мат.ожидание в столбцах
    E(i,:) = var(A(:,i)); %дисперсия в столбцах
end

Добавлено через 15 секунд
Тема79,

Matlab M

clc, clear all
 
A = rand(10,10);
 
for i = 1:size(A,2)
    B(i,:) = mean(A(i,:)); %мат.ожидание в строках
    C(i,:) = var(A(i,:)); %дисперсия в строках
    D(i,:) = mean(A(:,i)); %мат.ожидание в столбцах
    E(i,:) = var(A(:,i)); %дисперсия в столбцах
end

0 / 0 / 0

Регистрация: 13.05.2013

Сообщений: 20

24.05.2016, 18:14

[ТС]

Все правильно. Это я ошибся. По формуле считает дисперсию ( сигма в квадрате), а мне нужно найти просто сигму. Взял корень квадратный и все получилось. Все спасибо за помощь.
А формулы я немного исправил:
Dc=var(A,0,1); % дисперсия по столбцам
Dr=var(A,0,2); % дисперсия по строкам
Так получается то, что мне нужно.

Matasin

93 / 91 / 23

Регистрация: 08.05.2016

Сообщений: 521

24.05.2016, 18:57

А так нельзя?

Matlab M

1
2
3

A=rand(10,10);
Dc=var(A);
Dr=var(A');

0 / 0 / 0

Регистрация: 13.05.2013

Сообщений: 20

24.05.2016, 20:23

[ТС]

Так даже лучше.

Источник

Оператор sum. Если Х – вектор, то команда sum(X) вычисляет сумму его компонент. Если Х – матрица, то sum(X) – вектор–строка, компонентами которой являются суммы элементов каждого столбца

æ	–1	2ö	sum(X) = (2; 6) .
матрицы X. Например, для матрицы X = ç			÷
ç	3	4	÷
è	ø

Функция tan. Используется в виде tan(Х), где Х – матрица или вектор. Возвращает аналогичные по размерам матрицу или вектор, элементы которых имеют значения тангенса соответствующих элементов матрицы или вектора Х.

Оператор tril. Команда tril(A) для квадратной матрицы А возвращает нижнюю треугольную матрицу. Оператор var. В форме var(X) или var(X,0) возвращает несмещённую оценку дисперсии вектора X. В

форме var(X,1) возвращает смещённую оценку дисперсии вектора X. Оператор while. Задаёт цикл. Используется следующим образом:

while <Условие> … Инструкции … end;

Цикл типа while выполняется до тех пор, пока выполняется <Условие>. Для прекращения выполнения цикла можно использовать оператор break.

Пример 2.7. X= –2:0.5:3; N=1;

while X(N)<0; X(N)= –X(N); N=N+1;

end;

Оператор zeros. Команда R=zeros(n) создаёт матрицу R размера n × n , состоящую из нулей. Команда R=zeros(m,n) создаёт матрицу нулей размера m × n . Команда R=zeros(А) образует матрицу R нулей такого же размера, как и матрица А.

В пакете stats статистических программ Matlab (каталогMatlabtoolboxstats) имеются программы расчёта плотностей вероятности и функций распределения для многих известных распределений. Имена функций для расчёта плотностей вероятности оканчиваются буквами pdf (probability density function)¸ а для расчёта функций распределения – буквами cdf (cumulative distribution function).

2.5.1. Функции Matlab для расчёта плотностей вероятности

y=unifpdf(x,a,b) – расчёт значения плотности вероятности в точке x для равномерного на промежутке (a ; b) распределения.

y=normpdf(x,m,sigma) – расчёт значения плотности вероятности в точке x для нормального распределения, где m – математическое ожидание, sigma – среднее квадратическое отклонение.

y=gampdf(x,a,b) – расчёт значения плотности вероятности в точке x для гамма–распределения с параметрами a, b.

y=exppdf(x,lambda) – расчёт значения плотности вероятности в точке x для экспоненциального распределения с параметром lambda, равным математическому ожиданию (!) случайной величины.

y=chi2pdf(x,k) – расчёт значения плотности вероятности в точке x для распределения χ2 с k степенями

свободы.

y=tpdf(x,k) – расчёт значения плотности вероятности в точке x для распределения Стьюдента с k степенями свободы.

y=fpdf(x,k1,k2) – расчёт значения плотности вероятности в точке x для распределения Фишера с k1, k2 степенями свободы.

2.5.2. Функции Matlab для расчёта функций распределения

y=unifcdf(x,a,b) – расчёт значения функции распределения в точке x для равномерного на промежутке (a ; b) распределения.

y=normcdf(x,m,sigma) – расчёт значения функции распределения в точке x для нормального распределения, где m – математическое ожидание, sigma – среднее квадратическое отклонение.

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

y=gamcdf(x,a,b) – расчёт значения функции распределения в точке x для гамма–распределения с параметрами a, b.

y=expcdf(x,lambda) – расчёт значения функции распределения в точке x для экспоненциального распределения с параметром lambda, равным математическому ожиданию (!) случайной величины.

y=chi2cdf(x,k) – расчёт значения функции распределения в точке x для распределения χ2 с k

степенями свободы.

y=tcdf(x,k) – расчёт значения функции распределения в точке x для распределения Стьюдента с k степенями свободы.

y=fcdf(x,k1,k2) – расчёт значения функции распределения в точке x для распределения Фишера с k1, k2 степенями свободы.

Замечание. Для расчёта значений гамма–функции в точке x в Matlab имеется функция y=gamma(x).

2.6. Алгоритмы моделирования случайных величин

Случайные числа с различными законами распределения обычно моделируются с помощью преобразований одного или нескольких независимых значений базовой случайной величины. Базовая случайная величина α – это случайная величина с распределением R(0; 1) (равномерным распределением

в интервале (0;1) ). Независимые случайные величины с распределением R(0; 1) обозначаются символами α1, α2 , …. В любой системе программирования имеется стандартная программа моделирования базовой

случайной величины (см. раздел 2.4, оператор rand).

Рассмотрим алгоритмы моделирования случайных величин, имеющих законы распределения, описанные в разделе 1 пособия.

Нормальное распределение N(m; σ)


	Алгоритм моделирования 1:		Алгоритм моделирования 2:
1)	зарезервировать константу	1)	ξ1 = 2α1 −1 , ξ2 = 2α2 −1;
	c = 2π ;	2)	s = ξ2	+ ξ2 ;

2)	r = − 2ln α1 ;		1	2
3) если s ³ 1, вернуться к п. 1;
3)	ϕ = cα2 ;	4) r =		;
− (2ln s) s
4)	X1 = r cos ϕ , X 2 = r sin ϕ ;	5)	X1 = ξ1r , X 2 = ξ2r ;
5)	X1 = m + σX1, X 2 = m + σX 2 .
6)	X1 = m + σX1 , X 2 = m + σX 2 .

В качестве случайного числа можно взять любое из чисел X1 и X 2 .

Равномерное распределение R(a; b) ( a < b )

Алгоритм моделирования:

X = a + (b − a)α .

Экспоненциальное распределение E(λ) ( l > 0 )

Алгоритм моделирования:

X = −λ−1 ln α .

Распределение χ2 с k степенями свободы χ2 (k)

Алгоритм моделирования: k

X= åui2 ,

i=1

где ui ~ N(0;1) – независимые случайные величины.

Распределение Стьюдента с k степенями свободы St(k)

Алгоритм моделирования:

X =	u	,

v k

где u ~ N(0;1) , v ~ χ2 (k) – независимые случайные величины.

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Распределение Фишера с k1 , k2 степенями свободы F(k1 ; k2 )

Алгоритм моделирования:

X = vk1 , wk2

где v ~ χ2 (k1) , w ~ χ2 (k2 ) – независимые случайные величины.

Замечание 1. Описанные алгоритмы позволяют получить только одно случайное число. Для получения массивов объёмом 300 используйте цикл for (см. раздел 2.4).

Замечание 2. В Matlab (см. раздел 2.4) имеется системная константа π : pi=3.1415926535897… Натуральный логарифм числа x можно получить с помощью оператора log. Синус (или косинус) числа

x можно получить с помощью операторов sin (или cos).

2.7.Средства Matlab для моделирования случайных величин

Впакете stats статистических программ Matlab (каталогMatlabtoolboxstats) имеются программы моделирования случайных чисел из многих известных законов распределения. Имена указанных функций оканчиваются буквами rnd.

y=unifrnd(a,b) – возвращает случайное число из равномерного на промежутке (a ; b) распределения.

y=normrnd(m,sigma) – возвращает случайное число из нормального распределения, где m – математическое ожидание, sigma – среднее квадратическое отклонение.

y=gamrnd(a,b) – возвращает случайное число из гамма–распределения с параметрами a, b. y=exprnd(lambda) – возвращает случайное число из экспоненциального распределения с параметром

lambda, равным математическому ожиданию случайной величины.

y=chi2rnd(k) – возвращает случайное число из распределения χ2 с k степенями свободы.

y=trnd(k) – возвращает случайное число из распределения Стьюдента с k степенями свободы. y=frnd(k1,k2) – возвращает случайное число из распределения Фишера с k1, k2 степенями свободы. Замечание. В Matlab имеется программа для моделирования многомерных случайных чисел с

нормальным распределением.

r=mvnrnd(m,sigma,N) – возвращает матрицу случайных чисел, выбранных из многомерного нормального распределения с вектором средних m и ковариационной матрицей sigma. Параметр N является количеством строк в r (количеством многомерных случайных чисел).

2.8. Средства Matlab для получения выборочных числовых характеристик и интервальных оценок

В пакете stats статистических программ Matlab (каталогMatlabtoolboxstats) имеются программы расчёта выборочных числовых характеристик, а также получения интервальных оценок параметров распределений. Имена указанных функций оканчиваются буквами fit.

normfit(X) – возвращает оценку математического ожидания для нормально распределённой генеральной совокупности, полученную по выборке X.

[m,sigma,m_int,sigma_int]=normfit(X,alpha) – возвращает несмещённые оценки и 100 ×(1– alpha) –

процентные доверительные интервалы для параметров нормально распределённой генеральной совокупности (математическое ожидание и среднее квадратическое отклонение) по выборке X.

expfit(X) – возвращает несмещённую оценку математического ожидания экспоненциального распределения, полученную по выборке X методом максимального правдоподобия.

[m,m_int]=expfit(X,alpha) – возвращает максимально правдоподобную оценку и 100·(1–alpha)- процентный доверительный интервал для математического ожидания экспоненциального распределения.

gamfit(X) – возвращает оценки параметров гамма–распределения, полученные по выборке X методом максимального правдоподобия.

[par,par_int]=gamfit(X,alpha) – возвращает максимально правдоподобные оценки и 100·(1–alpha)- процентные доверительные интервалы для параметров гамма–распределения.

unifit(X) – возвращает оценку параметра a равномерного распределения на (a; b) , полученную по

выборке X методом максимального правдоподобия.

[a,b,a_int,b_int]=unifit(X,alpha) – возвращает максимально правдоподобные оценки и 100·(1–alpha)- процентные доверительные интервалы для параметров равномерного распределения.

Замечание. По умолчанию необязательный параметр alpha=0,05, что соответствует 95-процентным доверительным интервалам.

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

2.9. Средства Matlab для нахождения квантилей Распределений

В пакете stats статистических программ Matlab (каталогMatlabtoolboxstats) имеются программы расчёта квантилей для многих известных распределений. Имена функций для расчёта квантилей оканчиваются буквами inv.

x=norminv(p,m,sigma) – возвращает значение квантили порядка p для нормального распределения с математическим ожиданием m и средним квадратическим отклонением sigma.

x=chi2inv(p,k) – возвращает значение квантили порядка p для распределения χ2 с k степенями

свободы.

x=tinv(p,k) – возвращает значение квантили порядка p для распределения Стьюдента с k степенями свободы.

x=finv(p,k1,k2) – возвращает значение квантили порядка p для распределения Фишера с k1, k2 степенями свободы.

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Соседние файлы в папке Теория веротяностей

Источник

Syntax

Description

Examples

Variance of Matrix

Variance of Array

Specify Variance Weight Vector

Specify Dimension for Variance

Variance of Array Page

Variance Excluding Missing Values

Variance and Mean

Input Arguments

A — Input array vector | matrix | multidimensional array | table | timetable

w — Weight 0 (default) | 1 | vector

dim — Dimension to operate along positive integer scalar

vecdim — Vector of dimensions vector of positive integers

nanflag — Missing value condition "includemissing" (default) | "includenan" | "omitmissing" | "omitnan"

Output Arguments

V — Variance scalar | vector | matrix | multidimensional array | table

M — Mean scalar | vector | matrix | multidimensional array | table

More About

Variance

Weighted Variance

Weighted Mean

Extended Capabilities

Tall Arrays Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Distributed Arrays Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Version History

R2023a: Perform calculations directly on tables and timetables

R2023a: Specify missing value condition

R2023a: Improved performance with small group size

R2022a: Return mean or weighted mean

R2018b: Operate on multiple dimensions

Syntax

Description

Examples

Variance of a Fitted Distribution

Variance of Skewed Distribution

Variance of Triangular Distribution

Variance of a Kernel Distribution

Input Arguments

Output Arguments

v — Variance nonnegative scalar value

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Version History

Синтаксис

Описание

Примеры

Отклонение матрицы

Отклонение массива

Определение вектора веса отклонения

Определение размерности для отклонения

Отклонение страницы массивов

Отклонение, исключая NaN

Входные параметры

A — Входной массив вектор | матрица | многомерный массив

w — Вес0 (значение по умолчанию) | 1 | вектор

dim — Размерность, которая задает направление расчета положительный целочисленный скаляр

vecdim — Вектор из размерностей вектор из положительных целых чисел

nanflag NaN условие 'includenan' (значение по умолчанию) | 'omitnan'

Больше о

Дисперсия

Расширенные возможности

“Высокие” массивы Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++ Генерация кода C и C++ с помощью MATLAB® Coder™.

Генерация кода графического процессора Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Основанная на потоке среда Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.

Массивы графического процессора Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Распределенные массивы Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Дисперсия и мат.ожидание в матрице

2.6. Алгоритмы моделирования случайных величин

2.7.Средства Matlab для моделирования случайных величин

2.8. Средства Matlab для получения выборочных числовых характеристик и интервальных оценок

2.9. Средства Matlab для нахождения квантилей Распределений

Вам также может понравиться

`A` — Input array
vector | matrix | multidimensional array | table | timetable

`w` — Weight
`0` (default) | `1` | vector

`dim` — Dimension to operate along
positive integer scalar

`vecdim` — Vector of dimensions
vector of positive integers

`nanflag` — Missing value condition
`"includemissing"` (default) | `"includenan"` | `"omitmissing"` | `"omitnan"`

`V` — Variance
scalar | vector | matrix | multidimensional array | table

`M` — Mean
scalar | vector | matrix | multidimensional array | table

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment
Run code in the background using MATLAB® `backgroundPool` or accelerate code with Parallel Computing Toolbox™ `ThreadPool`.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

`v` — Variance
nonnegative scalar value

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

`Отклонение, исключая NaN`

`A` — Входной массив
вектор | матрица | многомерный массив

`w` — Вес
0 (значение по умолчанию) | `1` | вектор

`dim` — Размерность, которая задает направление расчета
положительный целочисленный скаляр

`vecdim` — Вектор из размерностей
вектор из положительных целых чисел

`nanflag` `NaN` условие
`'includenan'` (значение по умолчанию) | `'omitnan'`

“Высокие” массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.