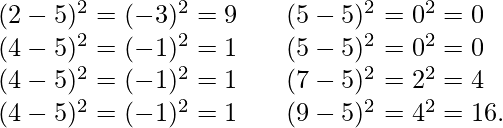Numpy in Python is a general-purpose array-processing package. It provides a high-performance multidimensional array object and tools for working with these arrays. It is the fundamental package for scientific computing with Python. Numpy provides very easy methods to calculate the average, variance, and standard deviation.
Average
Average a number expressing the central or typical value in a set of data, in particular the mode, median, or (most commonly) the mean, which is calculated by dividing the sum of the values in the set by their number. The basic formula for the average of n numbers x1, x2, ……xn is
Example:
Suppose there are 8 data points,
The average of these 8 data points is,
Average in Python Using Numpy:
One can calculate the average by using numpy.average() function in python.
Syntax:
numpy.average(a, axis=None, weights=None, returned=False)
Parameters:
a: Array containing data to be averaged
axis: Axis or axes along which to average a
weights: An array of weights associated with the values in a
returned: Default is False. If True, the tuple is returned, otherwise only the average is returned
Example 1:
Python
import numpy as np
list = [2, 4, 4, 4, 5, 5, 7, 9]
print(np.average(list))
Output:
5.0
Example 2:
Python
import numpy as np
list = [2, 40, 2, 502, 177, 7, 9]
print(np.average(list))
Output:
105.57142857142857
Variance
Variance is the sum of squares of differences between all numbers and means. The mathematical formula for variance is as follows,
Where,
? is Mean,
N is the total number of elements or frequency of distribution.
Example:
Let’s consider the same dataset that we have taken in average. First, calculate the deviations of each data point from the mean, and square the result of each,
Variance in Python Using Numpy:
One can calculate the variance by using numpy.var() function in python.
Syntax:
numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>)
Parameters:
a: Array containing data to be averaged
axis: Axis or axes along which to average a
dtype: Type to use in computing the variance.
out: Alternate output array in which to place the result.
ddof: Delta Degrees of Freedom
keepdims: If this is set to True, the axes which are reduced are left in the result as dimensions with size one
Example 1:
Python
import numpy as np
list = [2, 4, 4, 4, 5, 5, 7, 9]
print(np.var(list))
Output:
4.0
Example 2:
Python
import numpy as np
list = [212, 231, 234, 564, 235]
print(np.var(list))
Output:
18133.359999999997
Standard Deviation
Standard Deviation is the square root of variance. It is a measure of the extent to which data varies from the mean. The mathematical formula for calculating standard deviation is as follows,
Example:
Standard Deviation for the above data,
Standard Deviation in Python Using Numpy:
One can calculate the standard deviation by using numpy.std() function in python.
Syntax:
numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>)
Parameters:
a: Array containing data to be averaged
axis: Axis or axes along which to average a
dtype: Type to use in computing the variance.
out: Alternate output array in which to place the result.
ddof: Delta Degrees of Freedom
keepdims: If this is set to True, the axes which are reduced are left in the result as dimensions with size one
Example 1:
Python
import numpy as np
list = [2, 4, 4, 4, 5, 5, 7, 9]
print(np.std(list))
Output:
2.0
Example 2:
Python
import numpy as np
list = [290, 124, 127, 899]
print(np.std(list))
Output:
318.35750344541907
Last Updated :
08 Oct, 2021
Like Article
Save Article
Введение Два тесно связанных статистических показателя позволят нам получить представление о разбросе или разбросе наших данных. Первая мера – это дисперсия, которая измеряет, насколько далеки от среднего значения отдельные наблюдения в наших данных. Второй – это стандартное отклонение, которое представляет собой квадратный корень из дисперсии и измеряет степень вариации или дисперсии набора данных. В этом руководстве мы узнаем, как рассчитать дисперсию и стандартное отклонение в Python. Сначала мы будем
Вступление
Два тесно связанных статистических показателя позволят нам получить
представление о разбросе или разбросе наших данных. Первая мера – это
дисперсия , которая измеряет, насколько далеки от среднего значения
отдельные наблюдения в наших данных. Второе – стандартное отклонение ,
которое представляет собой квадратный корень из дисперсии и измеряет
степень вариации или дисперсии набора данных.
В этом руководстве мы узнаем, как рассчитать дисперсию и стандартное
отклонение в Python. Сначала мы закодируем функцию Python для каждой
меры, а позже мы узнаем, как использовать statistics Python для
быстрого выполнения той же задачи.
Обладая этими знаниями, мы сможем сначала взглянуть на наши наборы
данных и получить быстрое представление об общем разбросе наших данных.
Расчет дисперсии
В статистике дисперсия – это мера того, насколько отдельные
(числовые) значения в наборе данных отличаются от среднего или среднего
значения . Дисперсия
часто используется для количественной оценки разброса или дисперсии.
Распространение – это
характеристикавыборки
или генеральной
совокупности,
которая описывает степень ее изменчивости.
Высокая дисперсия говорит нам о том, что значения в нашем наборе данных
далеки от своего среднего. Таким образом, наши данные будут иметь
высокий уровень изменчивости. С другой стороны, низкая дисперсия говорит
нам о том, что значения довольно близки к среднему. В этом случае данные
будут иметь низкий уровень изменчивости.
Чтобы вычислить дисперсию в наборе данных, нам сначала нужно найти
разницу между каждым отдельным значением и средним значением. Дисперсия
- это среднее квадратов этих различий. Мы можем выразить дисперсию с
помощью следующего математического выражения:
$$
sigma ^ 2 = frac {1} {n} { sum_ {i = 0} ^ {n-1} {(x_i –
mu) ^ 2}}
$
В этом уравнении x ~i~ обозначает отдельные значения или наблюдения
в наборе данных. μ обозначает среднее или среднее значение этих
значений. n – количество значений в наборе данных.
Член x ~i~ – μ называется отклонением от среднего . Итак,
дисперсия – это среднее квадратическое отклонение. Поэтому мы обозначили
его как ^2^ .
Скажем, у нас есть набор данных [3, 5, 2, 7, 1, 3]. Чтобы найти его
дисперсию, нам нужно вычислить среднее значение:
$$
(3 + 5 + 2 + 7 + 1 + 3) / 6 = 3,5
$
Затем нам нужно вычислить сумму квадратного отклонения от среднего
значения всех наблюдений. Вот как:
$$
(3 – 3,5) ^ 2 + (5 – 3,5) ^ 2 + (2 – 3,5) ^ 2 + (7 – 3,5) ^ 2 + (1 –
3,5) ^ 2 + (3 – 3,5) ^ 2 = 23,5
$
Чтобы найти дисперсию, нам просто нужно разделить этот результат на
количество наблюдений следующим образом:
$$
23,5 / 6 = 3,916666667
$
Это все. Разница наших данных составляет 3,916666667. Дисперсию сложно
понять и интерпретировать, особенно насколько странны ее единицы.
Например, если наблюдения в нашем наборе данных измеряются в фунтах,
тогда дисперсия будет измеряться в квадратных фунтах. Итак, мы можем
сказать, что наблюдения составляют в среднем 3,916666667 квадратных
фунтов, что далеко от среднего значения 3,5. К счастью, стандартное
отклонение помогает решить эту проблему, но это тема следующего раздела.
Если мы применим концепцию дисперсии к набору данных, то сможем
различить дисперсию выборки и дисперсию генеральной совокупности
. Дисперсия генеральной совокупности – это дисперсия, которую мы
видели раньше, и мы можем вычислить ее, используя данные из полной
^генеральной совокупности и выражение для 2^ .
Дисперсия выборки обозначается как S ^2,^ и мы можем вычислить ее,
используя выборку из данной генеральной совокупности и следующее
выражение:
$$
S ^ 2 = frac {1} {n} { sum_ {i = 0} ^ {n-1} {(x_i – X) ^ 2}}
$
Это выражение очень похоже на выражение для вычисления ^2,^ но в
этом случае x ~i~ представляет отдельные наблюдения в выборке, а
X – это среднее значение выборки.
S ^2^ обычно используется для оценки дисперсии генеральной
^совокупности (2^ ) с использованием выборки данных. Однако S ^2^
систематически недооценивает дисперсию населения. По этой причине его
называют предвзятой оценкой дисперсии совокупности.
Когда у нас есть большая выборка, S ^2^ может быть адекватной
оценкой ^2^ . Для небольших образцов он, как правило, слишком
низкий. К счастью, есть еще одна простая статистика, которую мы можем
использовать для более точной ^оценки σ 2^ . Вот его уравнение:
$$
S ^ 2_ {n-1} = frac {1} {n-1} { sum_ {i = 0} ^ {n-1} {(x_i – X)
^ 2}}
$
Это очень похоже на предыдущее выражение. Это похоже на квадрат
отклонения от среднего, но в этом случае мы делим на n – 1 вместо
n . Это называется поправкой
Бесселя . Поправка
Бесселя показывает, что S ^2^ ~n-1~ является наилучшей несмещенной
оценкой дисперсии генеральной совокупности. Итак, на практике мы будем
использовать это уравнение для оценки дисперсии генеральной совокупности
с использованием выборки данных. Обратите внимание, что S ^2^ ~n-1~
также известен как дисперсия с n – 1 степенями свободы.
Теперь, когда мы узнали, как вычислить дисперсию с помощью
математического выражения, пора приступить к действию и вычислить
дисперсию с помощью Python.
Кодирование функции variance () в Python
Чтобы вычислить дисперсию, мы собираемся закодировать функцию Python под
названием variance() . Эта функция возьмет некоторые данные и вернет
их дисперсию. Внутри variance() мы собираемся вычислить среднее
значение данных и квадратные отклонения от среднего. Наконец, мы
собираемся вычислить дисперсию, найдя среднее значение отклонений.
Вот возможная реализация variance() :
>>> def variance(data):
... # Number of observations
... n = len(data)
... # Mean of the data
... mean = sum(data) / n
... # Square deviations
... deviations = [(x - mean) ** 2 for x in data]
... # Variance
... variance = sum(deviations) / n
... return variance
...
>>> variance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5.76
Сначала мы вычисляем количество наблюдений ( n ) в наших данных,
используя встроенную функцию
len() . Затем
мы вычисляем среднее значение данных, деля общую сумму наблюдений на
количество наблюдений.
Следующий шаг – вычислить квадратные отклонения от среднего. Для этого
мы используем понимание list
которое создает list квадратных отклонений с использованием выражения
(x - mean) ** 2 где x обозначает каждое наблюдение в наших данных.
Наконец, мы вычисляем дисперсию, суммируя отклонения и деля их на
количество наблюдений n .
В этом случае variance() вычислит дисперсию генеральной совокупности,
потому что мы используем n вместо n – 1 для вычисления среднего
значения отклонений. Если мы работаем с выборкой и хотим оценить
дисперсию генеральной совокупности, то нам нужно обновить выражение
variance = sum(deviations) / n до
variance = sum(deviations) / (n - 1) .
Мы можем реорганизовать нашу функцию, чтобы сделать ее более краткой и
эффективной. Вот пример:
>>> def variance(data, ddof=0):
... n = len(data)
... mean = sum(data) / n
... return sum((x - mean) ** 2 for x in data) / (n - ddof)
...
>>> variance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5.76
>>> variance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5], ddof=1)
6.4
В этом случае мы удаляем некоторые промежуточные шаги и временные
переменные, такие как deviations и variance . Мы также превращаем
понимание list в выражение генератора , что
намного эффективнее с точки зрения потребления памяти.
Обратите внимание, что эта реализация принимает второй аргумент,
называемый ddof который по
умолчанию 0 . Этот аргумент
позволяет нам установить степени свободы, которые мы хотим использовать
при вычислении дисперсии. Например, ddof=0 позволит нам вычислить
дисперсию генеральной совокупности. Между тем, ddof=1 позволит нам
оценить дисперсию генеральной совокупности с использованием выборки
данных.
Использование Python pvariance () и variance ()
Python включает стандартный модуль, называемый
statistics
который предоставляет некоторые функции для вычисления базовой
статистики данных. В этом случае
statistics.pvariance()
и
statistics.variance()
- это функции, которые мы можем использовать для вычисления дисперсии
генеральной совокупности и выборки соответственно.
Вот как работает Python pvariance() :
>>> import statistics
>>> statistics.pvariance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5.760000000000001
Нам просто нужно
импортировать statistics
а затем вызвать pvariance() с нашими данными в качестве аргумента. Это
вернет дисперсию населения.
С другой стороны, мы можем использовать Python variance() для
вычисления дисперсии выборки и использовать ее для оценки дисперсии всей
генеральной совокупности. Это потому, что variance() использует n –
1 вместо n для вычисления дисперсии. Вот как это работает:
>>> import statistics
>>> statistics.variance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
6.4
Это выборочная дисперсия S ^2^ . Таким образом, результатом
использования Python variance() должна быть объективная оценка
дисперсии совокупности ^2^ при условии, что наблюдения
репрезентативны для всей совокупности.
Расчет стандартного отклонения
Стандартное отклонение измеряет степень вариации или
дисперсии набора
числовых значений. Стандартное отклонение представляет собой квадратный
корень из дисперсии σ ^2^ и обозначается как σ. Итак, если мы
хотим вычислить стандартное отклонение, то все, что нам нужно сделать,
это извлечь квадратный корень из дисперсии следующим образом:
$$
sigma = sqrt { sigma ^ 2}
$
Опять же, нам нужно различать стандартное отклонение генеральной
совокупности
^, которое представляет собой квадратный корень из дисперсии генеральной совокупности (2^
), и стандартное отклонение выборки, которое является квадратным корнем
из выборочной дисперсии ( S ^2^ ). Обозначим стандартное отклонение
выборки как S :
$$
S = sqrt {S ^ 2}
$
Низкие значения стандартного отклонения говорят нам о том, что отдельные
значения ближе к среднему. С другой стороны, высокие значения говорят
нам о том, что отдельные наблюдения далеки от среднего значения данных.
Значения, которые находятся в пределах одного стандартного отклонения от
среднего, можно рассматривать как довольно типичные, тогда как значения,
которые отличаются от среднего на три или более стандартных отклонения,
могут считаться гораздо более нетипичными. Их также называют
выбросами .
В отличие от дисперсии, стандартное отклонение будет выражаться в тех же
единицах, что и исходные наблюдения. Следовательно, стандартное
отклонение – более значимая и легкая для понимания статистика. Повторяя
наш пример, если наблюдения выражены в фунтах, то стандартное отклонение
также будет выражено в фунтах.
Если мы пытаемся оценить стандартное отклонение генеральной совокупности
с использованием выборки данных, тогда нам будет удобнее использовать
n – 1 степень свободы. Вот математическое выражение, которое мы
обычно используем для оценки дисперсии совокупности:
$
sigma_x = sqrt frac { sum_ {i = 0} ^ {n-1} {(x_i – mu_x)
^ 2}} {n-1}
$
Обратите внимание, что это квадратный корень из дисперсии выборки с **n
- 1** степенями свободы. Это равносильно тому, чтобы сказать:
$
S_ {n-1} = sqrt {S ^ 2_ {n-1}}
$
Как только мы узнаем, как рассчитать стандартное отклонение с
использованием его математического выражения, мы можем взглянуть на то,
как мы можем вычислить эту статистику с помощью Python.
Кодирование функции stdev () на Python
Чтобы вычислить стандартное отклонение набора данных, мы будем
полагаться на нашу функцию variance() Мы также собираемся использовать
функцию
sqrt()
math модуля стандартной библиотеки
Python. Вот функция stdev() которая берет данные из совокупности и
возвращает ее стандартное отклонение:
>>> import math
>>> # We relay on our previous implementation for the variance
>>> def variance(data, ddof=0):
... n = len(data)
... mean = sum(data) / n
... return sum((x - mean) ** 2 for x in data) / (n - ddof)
...
>>> def stdev(data):
... var = variance(data)
... std_dev = math.sqrt(var)
... return std_dev
>>> stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
2.4
Наша stdev() принимает некоторые data и возвращает стандартное
отклонение генеральной совокупности. Для этого мы полагаемся на нашу
предыдущую variance() для вычисления дисперсии, а затем с помощью
math.sqrt() извлекаем квадратный корень из дисперсии.
Если мы хотим использовать stdev() для оценки стандартного отклонения
генеральной совокупности с использованием выборки данных, нам просто
нужно вычислить дисперсию с n – 1 степенями свободы, как мы видели
ранее. Вот более общий stdev() который также позволяет передавать
степени свободы:
>>> def stdev(data, ddof=0):
... return math.sqrt(variance(data, ddof))
>>> stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
2.4
>>> stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5], ddof=1)
2.5298221281347035
В этой новой реализации мы можем использовать ddof=0 для вычисления
стандартного отклонения генеральной совокупности или мы можем
использовать ddof=1 для оценки стандартного отклонения генеральной
совокупности с использованием выборки данных.
Использование Python pstdev () и stdev ()
Модуль statistics Python также предоставляет функции для расчета
стандартного отклонения. Мы можем найти
pstdev()
и
stdev()
. Первая функция берет данные о генеральной совокупности и возвращает ее
стандартное отклонение. Вторая функция берет данные из выборки и
возвращает оценку стандартного отклонения генеральной совокупности.
Вот как работают эти функции:
>>> import statistics
>>> statistics.pstdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
2.4000000000000004
>>> statistics.stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
2.5298221281347035
Сначала нам нужно
импортировать модуль
statistics Затем мы можем вызвать statistics.pstdev() с данными по
генеральной совокупности, чтобы получить ее стандартное отклонение.
Если у нас нет данных для всей генеральной совокупности, что является
обычным сценарием, мы можем использовать выборку данных и использовать
statistics.stdev() для оценки стандартного отклонения генеральной
совокупности.
Заключение
Дисперсия и стандартное отклонение обычно используются для
измерения изменчивости или дисперсии набора данных. Эти статистические
показатели дополняют использование среднего, медианы и
режима при описании наших
данных.
В этом руководстве мы узнали, как рассчитать дисперсию и стандартное
отклонение набора данных с помощью Python. Сначала мы шаг за шагом
научились создавать наши собственные функции для их вычисления, а позже
мы узнали, как использовать модуль statistics Python как быстрый
способ приблизиться к их вычислению.
17 авг. 2022 г.
читать 1 мин
Дисперсия — это способ измерения разброса значений в наборе данных.
Формула для расчета дисперсии населения :
σ 2 = Σ (xi – μ) 2 / N
куда:
- Σ : символ, означающий «сумма».
- μ : Среднее значение населения
- x i : i -й элемент из совокупности
- N : Численность населения
Формула для расчета выборочной дисперсии :
s 2 = Σ (x i – x ) 2 / (n-1)
куда:
- x : выборочное среднее
- x i : i -й элемент из выборки
- n : размер выборки
Мы можем использовать функции дисперсии и pдисперсии из библиотеки статистики в Python, чтобы быстро вычислить выборочную дисперсию и дисперсию генеральной совокупности (соответственно) для данного массива.
from statistics import variance, pvariance
#calculate sample variance
variance(x)
#calculate population variance
pvariance(x)
В следующих примерах показано, как использовать каждую функцию на практике.
Пример 1: Расчет выборочной дисперсии в Python
Следующий код показывает, как вычислить выборочную дисперсию массива в Python:
from statistics import variance
#define data
data = [4, 8, 12, 15, 9, 6, 14, 18, 12, 9, 16, 17, 17, 20, 14]
#calculate sample variance
variance(data)
22.067
Выборочная дисперсия оказывается равной 22,067 .
Пример 2: Расчет дисперсии населения в Python
Следующий код показывает, как вычислить дисперсию совокупности массива в Python:
from statistics import pvariance
#define data
data = [4, 8, 12, 15, 9, 6, 14, 18, 12, 9, 16, 17, 17, 20, 14]
#calculate sample variance
pvariance(data)
20.596
Дисперсия населения оказывается равной 20,596 .
Примечания по расчету выборки и дисперсии генеральной совокупности
При расчете дисперсии выборки и генеральной совокупности следует учитывать следующее:
- Вы должны вычислить дисперсию совокупности , когда набор данных, с которым вы работаете, представляет всю совокупность, то есть каждое значение, которое вас интересует.
- Вы должны рассчитать выборочную дисперсию , когда набор данных, с которым вы работаете, представляет собой выборку, взятую из большей интересующей совокупности.
- Выборочная дисперсия данного массива данных всегда будет больше, чем дисперсия генеральной совокупности для того же массива данных, потому что при расчете дисперсии выборки больше неопределенности, поэтому наша оценка дисперсии будет больше.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать другие показатели распространения в Python:
Как рассчитать межквартильный диапазон в Python
Как рассчитать коэффициент вариации в Python
Как рассчитать стандартное отклонение списка в Python
Этот заключительный пост посвящен анализу дисперсии. Предыдущий пост см. здесь.
Анализ дисперсии
Анализ дисперсии (варианса), который в специальной литературе также обозначается как ANOVA от англ. ANalysis Of VAriance, — это ряд статистических методов, используемых для измерения статистической значимости расхождений между группами. Он был разработан чрезвычайно одаренным статистиком Рональдом Фишером, который также популяризировал процедуру проверки статистической значимости в своих исследовательских работах по биологическому тестированию.
Примечание. В предыдущей и этой серии постов для термина «variance» использовался принятый у нас термин «дисперсия» и в скобках местами указывался термин «варианс». Это не случайно. За рубежом существуют парные термины «variance» и «covariance», и они по идее должны переводиться с одним корнем, например, как «варианс» и «коварианс», однако на деле у нас парная связь разорвана, и они переводятся как совершенно разные «дисперсия» и «ковариация». Но это еще не все. «Dispersion» (статистическая дисперсия) за рубежом является отдельным родовым понятием разбросанности, т.е. степени, с которой распределение растягивается или сжимается, а мерами статистической дисперсии являются варианс, стандартное отклонение и межквартильный размах. Dispersion, как родовое понятие разбросанности, и variance, как одна из ее мер, измеряющая расстояние от среднего значения – это два разных понятия. Далее в тексте для variance везде будет использоваться общепринятый термин «дисперсия». Однако данное расхождение в терминологии следует учитывать.
Наши тесты на основе z-статистики и t-статистики были сосредоточены на выборочных средних значениях как первостепенном механизме проведения разграничения между двумя выборками. В каждом случае мы искали расхождение в средних значениях, деленных на уровень расхождения, который мы могли обоснованно ожидать, и количественно выражали стандартной ошибкой.
Среднее значение не является единственным выборочным индикатором, который может указывать на расхождение между выборками. На самом деле, в качестве индикатора статистического расхождения можно также использовать выборочную дисперсию.
В целях иллюстрации того, как это могло бы работать, рассмотрим приведенную выше диаграмму. Каждая из трех групп слева может представлять выборки времени пребывания на конкретном веб-сайте с его собственным средним значением и стандартным отклонением. Если время пребывания для всех трех групп объединить в одну, то дисперсия будет больше средней дисперсии для групп, взятых отдельно.
Статистическая значимость на основе анализа дисперсии вытекает из соотношения двух дисперсий — дисперсии между исследуемыми группами и дисперсии внутри исследуемых групп. Если существует значимое межгрупповое расхождение, которое не отражено внутри групп, то эти группы помогают объяснить часть дисперсии между группами. И напротив, если внутригрупповая дисперсия идентична межгрупповой дисперсии, то группы статистически от друг друга неразличимы.
F-распределение
F-распределение параметризуется двумя степенями свободы — степенями свободы размера выборки и числа групп.
Первая степень свободы — это количество групп минус 1, и вторая степень свободы — размер выборки минус число групп. Если k представляет число групп, и n — объем выборки, то получаем:
Мы можем визуализировать разные F-распределения на графике при помощи функции библиотеки pandas plot:
def ex_2_Fisher():
'''Визуализация разных F-распределений на графике'''
mu = 0
d1_values, d2_values = [4, 9, 49], [95, 90, 50]
linestyles = ['-', '--', ':', '-.']
x = sp.linspace(0, 5, 101)[1:]
ax = None
for (d1, d2, ls) in zip(d1_values, d2_values, linestyles):
dist = stats.f(d1, d2, mu)
df = pd.DataFrame( {0:x, 1:dist.pdf(x)} )
ax = df.plot(0, 1, ls=ls,
label=r'$d_1=%i, d_2=%i$' % (d1,d2), ax=ax)
plt.xlabel('$x$nF-статистика')
plt.ylabel('Плотность вероятности n$p(x|d_1, d_2)$')
plt.show()Кривые приведенного выше графика показывают разные F-распределения для выборки, состоящей из 100 точек, разбитых на 5, 10 и 50 групп.
F-статистика
Тестовая выборочная величина, которая представляет соотношение дисперсии внутри и между группами, называется F-статистикой. Чем ближе значение F-статистики к единице, тем более похожи обе дисперсии. F-статистика вычисляется очень просто следующим образом:
где S2b — это межгрупповая дисперсия, и S2w — внутригрупповая дисперсия.
По мере увеличения соотношения F межгрупповая дисперсия увеличивается по сравнению с внутригрупповой. Это означает, что это разбиение на группы хорошо справляется с задачей объяснения дисперсии, наблюдавшейся по всей выборке в целом. Там, где это соотношение превышает критический порог, мы можем сказать, что расхождение является статистически значимым.
F-тест всегда является односторонним, потому что любая дисперсия среди групп демонстрирует тенденцию увеличивать F. При этом F не может уменьшаться ниже нуля.
Внутригрупповая дисперсия для F-теста вычисляется как среднеквадратичное отклонение от среднего значения. Мы вычисляем ее как сумму квадратов отклонений от среднего значения, деленную на первую степень свободы. Например, если имеется k групп, каждая со средним значением x̅k, то мы можем вычислить внутригрупповую дисперсию следующим образом:
где SSW — это внутригрупповая сумма квадратов, и xjk — это значение j-ого элемента в группе .
Приведенная выше формула для вычисления SSW имеет грозный вид, но на деле довольно легко имплементируется на Python, как сумма квадратичных отклонений от среднего значения ssdev, делающая вычисление внутригрупповой суммы квадратов тривиальным:
def ssdev( xs ):
'''Сумма квадратов отклонений между
каждым элементом и средним по выборке'''
mu = xs.mean()
square_deviation = lambda x : (x - mu) ** 2
return sum( map(square_deviation, xs) )Межгрупповая дисперсия для F-теста имеет похожую формулу:
где SST — это полная сумма квадратов отклонений, и SSW — значение, которое мы только что вычислили. Полная сумма квадратов является суммой квадратичных расхождений от «итогового» среднего значения, которую можно вычислить следующим образом:
Отсюда, SST — это попросту полная сумма квадратов без какого-либо разбиения на группы. На языке Python значения SST и SSW вычисляются элементарно, как будет показано ниже.
ssw = sum( groups.apply( lambda g: ssdev(g) ) ) # внутригрупповая сумма
# квадратов отклонений
sst = ssdev( df['dwell-time'] ) # полная сумма квадратов по всему набору
ssb = sst – ssw # межгрупповая сумма квадратов отклоненийF-статистика вычисляется как отношение межгрупповой дисперсии к внутригрупповой. Объединив определенные ранее функции ssb и ssw и две степени свободы, мы можем вычислить F-статистика.
На языке Python F-статистика из групп и двух степеней свободы вычисляется следующим образом:
msb = ssb / df1 # усредненная межгрупповая
msw = ssw / df2 # усредненная внутригрупповая
f_stat = msb / mswИмея возможность вычислить F-статистику из групп, мы теперь готовы использовать его в соответствующем F-тесте.
F-тест
Как и в случае со всеми проверками статистических гипотез, которые мы рассмотрели в этой серии постов, как только имеется выборочная величина (статистика) и распределение, нам попросту нужно подобрать значение уровня значимости и посмотреть, не превысили ли наши данные критическое для теста значение.
Библиотека scipy предлагает функцию stats.f.sf, но она измеряет дисперсию между и внутри всего двух групп. В целях выполнения F-теста на наших 20 разных группах, нам придется имплементировать для нее нашу собственную функцию. К счастью, мы уже проделали всю тяжелую работу в предыдущих разделах, вычислив надлежащую F-статистику. Мы можем выполнить F-тест, отыскав F-статистику в F-распределении, параметризованном правильными степенями свободы. В следующем ниже примере мы напишем функцию f_test, которая все это использует для выполнения теста на произвольном числе групп:
def f_test(groups):
m, n = len(groups), sum(groups.count())
df1, df2 = m - 1, n - m
ssw = sum( groups.apply(lambda g: ssdev(g)) )
sst = ssdev( df['dwell-time'] )
ssb = sst - ssw
msb = ssb / df1
msw = ssw / df2
f_stat = msb / msw
return stats.f.sf(f_stat, df1, df2)
def ex_2_24():
'''Проверка вариантов дизайна веб-сайта на основе F-теста'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
return f_test(groups)0.014031745203658217В последней строке приведенной выше функции мы преобразуем значение F-статистики в p-значение, пользуясь функцией scipy stats.f.sf, параметризованной правильными степенями свободы. P-значение является мерой всей модели, т.е. насколько хорошо разные веб-сайты объясняют дисперсию времени пребывания в целом. Нам остается только выбрать уровень значимости и выполнить проверку. Будем придерживаться 5%-ого уровня значимости.
Проверка возвращает p-значение, равное 0.014, т.е. значимый результат. Разные варианты веб-сайта действительно имеют разные дисперсии, которые нельзя просто объяснить одной лишь случайной ошибкой в выборке.
Для визуализации распределений всех вариантов дизайна веб-сайта на одном графике мы можем воспользоваться коробчатой диаграммой, разместив распределения для сопоставления рядом друг с другом:
def ex_2_25():
'''Визуализация распределений всех вариантов
дизайна веб-сайта на одной коробчатой диаграмме'''
df = load_data('multiple-sites.tsv')
df.boxplot(by='site', showmeans=True)
plt.xlabel('Номер дизайна веб-сайта')
plt.ylabel('Время пребывания, сек.')
plt.title('')
plt.suptitle('')
plt.show()В приведенном выше примере показана работа функции boxplot, которая вычисляет свертку на группах и сортирует группы по номеру варианта дизайна веб-сайта. Соответственно наш изначальный веб-сайт с номером 0, на графике расположен крайним слева.
Может создастся впечатление, что вариант дизайна веб-сайта с номером 10 имеет самое длительное время пребывания, поскольку его межквартильный размах простирается вверх выше других. Однако, если вы присмотритесь повнимательнее, то увидите, что его среднее значение меньше, чем у варианта дизайна с номером 6, имеющего среднее время пребывания более 144 сек.:
def ex_2_26():
'''T-проверка вариантов 0 и 10 дизайна веб-сайта'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
site_0 = groups.get_group(0)
site_10 = groups.get_group(10)
_, p_val = stats.ttest_ind(site_0, site_10, equal_var=False)
return p_val0.0068811940138903786Подтвердив статистически значимый эффект при помощи F-теста, теперь мы вправе утверждать, что вариант дизайна веб-сайта с номером 6 статистически отличается от изначального значения:
def ex_2_27():
'''t-тест вариантов 0 и 6 дизайна веб-сайта'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
site_0 = groups.get_group(0)
site_6 = groups.get_group(6)
_, p_val = stats.ttest_ind(site_0, site_6, equal_var=False)
return p_val0.005534181712508717Наконец, у нас есть подтверждающие данные, из которых вытекает, что веб-сайт с номером 6 является подлинным улучшением существующего веб-сайта. В результате нашего анализа исполнительный директор AcmeContent санкционирует запуск обновленного дизайна веб-сайта. Веб-команда – в восторге!
Размер эффекта
В этой серии постов мы сосредоточили наше внимание на широко используемых в статистической науке методах проверки статистической значимости, которые обеспечивают обнаружение статистического расхождения, которое не может быть легко объяснено случайной изменчивостью. Мы должны всегда помнить, что выявление значимого эффекта — это не одно и то же, что и выявление большого эффекта. В случае очень больших выборок значимым будет считаться даже крошечное расхождение в выборочных средних. В целях более глубокого понимания того, является ли наше открытие значимым и важным, мы так же должны констатировать величину эффекта.
Интервальный индекс d Коэна
Индекс d Коэна — это поправка, которую применяется для того, чтобы увидеть, не является ли наблюдавшееся расхождение не просто статистически значимым, но и действительно большим. Как и поправка Бонферрони, она проста:
Здесь Sab — это объединенное стандартное отклонение (не объединенная стандартная ошибка) выборок. Она вычисляется аналогично вычислению объединенной стандартной ошибки:
def pooled_standard_deviation(a, b):
'''Объединенное стандартное отклонение
(не объединенная стандартная ошибка)'''
return sp.sqrt( standard_deviation(a) ** 2 +
standard_deviation(b) ** 2)Так, для варианта под номером 6 дизайна нашего веб-сайта мы можем вычислить индекс d Коэна следующим образом:
def ex_2_28():
'''Вычисление интервального индекса d Коэна
для варианта дизайна веб-сайта под номером 6'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(6)
return (b.mean() - a.mean()) / pooled_standard_deviation(a, b)0.38913648705499848В отличие от p-значений, абсолютный порог для индекса d Коэна отсутствует. Считать ли эффект большим или нет частично зависит от контекста, однако этот индекс действительно предоставляет полезную, нормализованную меру величины эффекта. Значения выше 0.5, как правило, считаются большими, поэтому значение 0.38 — это умеренный эффект. Он определенно говорит о значительном увеличении времени пребывания на нашем веб-сайте и что усилия, потраченные на обновление веб-сайта, определенно не были бесполезными.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Резюме
В этой серии постов мы узнали о разнице между описательной и инференциальной статистикой, занимающейся методами статистического вывода. Мы еще раз убедились в важности нормального распределения и центральной предельной теоремы, и научились квантифицировать расхождение с популяциями, используя проверку статистических гипотез на основе z-теста, t-теста и F-теста.
Мы узнали о том, каким именно образом методология инференциальной статистики анализирует непосредственно сами выборки, чтобы выдвигать утверждения о всей популяции в целом, из которой они были отобраны. Мы познакомились с целым рядом методов —интервалами уверенности, размножением выборок путем бутстрапирования и проверкой статистической значимости — которые помогают разглядеть глубинные параметры популяции. Симулируя многократные испытания, мы также получили представление о трудности проверки статистической значимости в условиях многократных сравнений и увидели, как F-тест помогает решать эту задачу и устанавливать равновесие между ошибками 1-го и 2-го рода.
Мы также коснулись терминологических болевых точек и выяснили некоторые нюансы смыслового дрейфа в отечественной статистике.
В следующей серии постов, если читатели пожелают, мы применим полученные знания о дисперсии и F-тесте к одиночным выборкам. Мы представим метод регрессионного анализа и воспользуемся им для обнаружения корреляции между переменными в выборке из спортсменов-олимпийцев.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Голосуйте 😉 за или против размещения следующей серии постов
Проголосовали 30 пользователей.
Воздержались 6 пользователей.
- numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>, *, where=<no value>)[source]#
-
Compute the variance along the specified axis.
Returns the variance of the array elements, a measure of the spread of a
distribution. The variance is computed for the flattened array by
default, otherwise over the specified axis.- Parameters:
-
- aarray_like
-
Array containing numbers whose variance is desired. If a is not an
array, a conversion is attempted. - axisNone or int or tuple of ints, optional
-
Axis or axes along which the variance is computed. The default is to
compute the variance of the flattened array.New in version 1.7.0.
If this is a tuple of ints, a variance is performed over multiple axes,
instead of a single axis or all the axes as before. - dtypedata-type, optional
-
Type to use in computing the variance. For arrays of integer type
the default isfloat64; for arrays of float types it is the same as
the array type. - outndarray, optional
-
Alternate output array in which to place the result. It must have
the same shape as the expected output, but the type is cast if
necessary. - ddofint, optional
-
“Delta Degrees of Freedom”: the divisor used in the calculation is
N - ddof, whereNrepresents the number of elements. By
default ddof is zero. - keepdimsbool, optional
-
If this is set to True, the axes which are reduced are left
in the result as dimensions with size one. With this option,
the result will broadcast correctly against the input array.If the default value is passed, then keepdims will not be
passed through to thevarmethod of sub-classes of
ndarray, however any non-default value will be. If the
sub-class’ method does not implement keepdims any
exceptions will be raised. - wherearray_like of bool, optional
-
Elements to include in the variance. See
reducefor
details.New in version 1.20.0.
- Returns:
-
- variancendarray, see dtype parameter above
-
If
out=None, returns a new array containing the variance;
otherwise, a reference to the output array is returned.
Notes
The variance is the average of the squared deviations from the mean,
i.e.,var = mean(x), wherex = abs(a - a.mean())**2.The mean is typically calculated as
x.sum() / N, whereN = len(x).
If, however, ddof is specified, the divisorN - ddofis used
instead. In standard statistical practice,ddof=1provides an
unbiased estimator of the variance of a hypothetical infinite population.
ddof=0provides a maximum likelihood estimate of the variance for
normally distributed variables.Note that for complex numbers, the absolute value is taken before
squaring, so that the result is always real and nonnegative.For floating-point input, the variance is computed using the same
precision the input has. Depending on the input data, this can cause
the results to be inaccurate, especially forfloat32(see example
below). Specifying a higher-accuracy accumulator using thedtype
keyword can alleviate this issue.Examples
>>> a = np.array([[1, 2], [3, 4]]) >>> np.var(a) 1.25 >>> np.var(a, axis=0) array([1., 1.]) >>> np.var(a, axis=1) array([0.25, 0.25])
In single precision, var() can be inaccurate:
>>> a = np.zeros((2, 512*512), dtype=np.float32) >>> a[0, :] = 1.0 >>> a[1, :] = 0.1 >>> np.var(a) 0.20250003
Computing the variance in float64 is more accurate:
>>> np.var(a, dtype=np.float64) 0.20249999932944759 # may vary >>> ((1-0.55)**2 + (0.1-0.55)**2)/2 0.2025
Specifying a where argument:
>>> a = np.array([[14, 8, 11, 10], [7, 9, 10, 11], [10, 15, 5, 10]]) >>> np.var(a) 6.833333333333333 # may vary >>> np.var(a, where=[[True], [True], [False]]) 4.0