Как найти дисперсию прибыли

What is Variance?

Variance is a metric that is needed to estimate the squared deviation of any random variable from the mean value. In the portfolio theory, the variance of return is called the measure of risk inherent in a singular or in an asset of portfolios.

In general, the higher the value of variance, the bigger is the squared deviation of return of the given portfolio from the expected rate. The higher values show a larger risk, and low values indicate a lower inherent risk.

Formula: How to Calculate Variance

We have two different approaches to calculate the variance of returns −

• Probability Approach
• Historical Return Approach

Probability Approach

The probability approach for determining variance is used when the complete set of possible outcomes is available. This means the probability distribution of the asset or portfolio is known in advance.

The equation of variance formula in the Probability approach can be written as follows −

$$mathrm{sigma^2 =displaystylesumlimits_{i=1}^n {}{(𝑟𝑖 − ERR)^2 × p_{𝑖}}}$$

Where,

• 𝑟_𝑖 is the rate of return achieved at i^th outcome,

• ERR is the expected rate of return,

• 𝑝_𝑖 is the probability of i^th outcome, and

• n is the number of possible outcomes.

Historical Return Approach

The historical return approach is more generally used in investing and finance. Using finite data set of the history of the investment in an asset or a portfolio, the return is calculated with assumptions that each possible outcome has the same probability. Thus, the variance of return on a single asset or portfolio is measured as −

$$mathrm{sigma^2 =frac{sum_{substack{i=1}}^n {(𝑟𝑖 − ERR)^2}}{N}}$$

where N is the size of the entire population.

The above formula considers the idea that a dataset represents the entire population, but in numerous practical situations, a sample of the given population is used instead of the entire population which may be very large. Therefore, a sample variance is an estimation of the variance of the entire population −

$$mathrm{{sigma_{substack{s}}^2}=frac{sum_{substack{i=1}}^n {(𝑟𝑖 − ERR_{s})^2}}{N− 1}}$$

where ERR_S is the expected rate of return of a sample or sample mean, and N is the size of the sample.

Favorable vs. Unfavorable Variance

As variance analysis is done for both revenues and expenses, it’s crucial to carefully distinguish between the two sides of impacts – the positive or negative impact.  For this reason, the terms favorable and unfavorable are used instead of saying positive, negative, over or under, etc., as they make the point clearer.

For example, if a cost has higher than expected difference to the forecast, that’s an unfavorable variance as it’s worse to have costs higher.

Variance in Budgeting and Forecasting

The variance formula is very useful in budgeting and forecasting. It gives a clear picture when analyzing results.  It helps the financial analyst to perform his duties appropriately and with utmost accuracy.

The role of Financial Planning & Analysis (FP&A) department is to provide the management with accurate, timely, and insightful information so that managers can take proactive decisions about the company. Working with variance is therefore crucial for the FP&A department.

Определим
теперь что дает диверсификация для
уменьшения риска
и выявим условия, когда эта цель
достигается. В качестве объекта
анализа примем некоторый абстрактный
портфель цен­ных бумаг (далее для
краткости — портфель). Такой выбор
объ­ясняется методологическими
преимуществами — в этом случае проще
выявить зависимости между основными
переменными. Однако
многие из полученных результатов без
большой натяж­ки можно распространить
и на производственные инвестиции.

В
предыдущем параграфе отмечалось, что
в качестве измери­теля
риска в долгосрочных финансовых операциях
широко рас­пространена такая мера,
как дисперсия дохода во времени.
Ди­версификация портфеля при правильном
ее применении при­водит к уменьшению
этой дисперсии при всех прочих равных
условиях. Диверсификация базируется
на простой гипотезе. Ес­ли каждая
компонента портфеля (в рассматриваемой
задаче — вид ценной бумаги) характеризуется
некоторой дисперсией до­хода, то доход
от портфеля имеет дисперсию, определяемую
его составом.
Таким образом, изменяя
состав портфеля, можно ме­нять суммарную
дисперсию дохода, а в некоторых случаях
свести ее
к минимуму.

Итак,
пусть имеется портфель из п
видов
ценных бумаг. До­ход от одной бумаги
вида / составляет величину d_r
Суммарный
доход (А),
очевидно,
равен

A
= 2a.d_i9 (8.1)

где
a_i
—
количество бумаг вида /.

Если
d_i
представляет
собой средний доход от бумаги вида /, то
величина А
характеризует
средний доход от портфеля бумаг в целом.

Для
начала положим, что показатели доходов
различных ви­дов бумаг являются
статистически независимыми величинами
(иначе говоря, не коррелируют между
собой). Дисперсия дохо­да портфеля
(обозначим ее как D)
в
этом случае находится как

Я-£*?А. (8.2)

/-1

171

где
D.
—
дисперсия дохода от бумаги вида /, п
—
количество видов ценных бумаг.

Для
упрощения, которое нисколько не повлияет
на резуль­таты
дальнейших рассуждений, перейдем от
абсолютного из­мерения количества
ценных бумаг к относительному. Пусть
теперь
а.
характеризует
долю в портфеле бумаги вида /, т.е. О <
а.
<
1, 21а.
= 1.

Для
зависимых в статистическом смысле
показателей дохода отдельных
бумаг дисперсию суммарного дохода
находим следу­ющим
образом:

^D
” %
^at^Di
+
2
2
^ai^aJ^rU°i°J>

(8.3)

где
D_f
—
дисперсия дохода от бумаги вида /, r_fJ
—
коэффициент корреляции
дохода от бумаг вида / и у, а_у
ис^.-
среднее квад-ратическое
отклонение дохода у бумаг вида / и у.

Коэффициент
корреляции двух случайных переменных
х
и
у,
как
известно, определяется по формуле¹

^г*у
=

%(х-х)(у-
у)

па_хо_у

(8.4)

где
х, у
—
средние (в нашем случае средние доходы
двух видов бумаг).

Для
расчетов часто применяется следующая
рабочая формула:

^пУ*у-У*Уу

‘ху

_{2*ЧХ*Пк>Ч5>)}

Поскольку
коэффициент корреляции может быть как
поло­жительной,
так и отрицательной величиной, то, как
это выте­кает
из (8.3), при
положительной корреляции дисперсия
суммарно-

1 Напомним следующие свойства коэффициента корреляции:

• коэффициент
  не имеет размерности, следовательно,
  он сопоставим для разных
  рядов данных;

• величина
  г_ху
  лежит
  в пределах от -1 до +1.
  Значение г_ху
  =
  +1 говорит о том, что между переменными
  существует полная положительная
  корреляция, т.
  е. наблюдается функциональная линейная
  зависимость — с увеличением х
  ли­нейно
  растет у.
  При
  г_ху
  =
  -1 наблюдается отрицательная линейная
  зависимость.

172

го
дохода увеличивается, при отрицательной
она сокращается. В
самом
деле, при заметной отрицательной
корреляции положи­тельные
отклонения от среднего дохода одних
бумаг погашают­ся
отрицательными отклонениями у других.
И наоборот, при положительной корреляции
отклонения суммируются, что уве­личивает
общую дисперсию и риск.

Проследим
теперь, каково влияние масштаба
диверсифика­ции на
размер риска. Под масштабом диверсификации
здесь бу­дем
понимать количество объектов, выбранных
для инвестиции (количество
видов ценных бумаг). Обратимся к условному
при­меру,
который позволяет наиболее отчетливо
выделить влияние указанного
фактора. Итак, пусть портфель состоит
из бумаг различного
вида, но имеющих одинаковую дисперсию
дохода (о^).
Удельные веса в портфеле каждого вида
бумаг также оди­наковы, а общая сумма
вложений равна 1. Положим, что пока­затели
доходности у отдельных видов бумаг
статистически не­зависимы, т.е.
применима формула (8.2). В этих условиях
для оценки
величины среднего квадратического
отклонения дохода портфеля
получим

п
°’

где
п
—
количество видов ценных бумаг.

Воспользуемся
приведенной формулой и определим
диспер­сию
дохода для портфеля, состоящего из двух
и трех видов бу­маг.
Так, для двух бумаг имеем

^D
–
2°о
^и
а“^2°°
“°’^71а°-

Для
трех видов бумаг квадратическое
отклонение портфеля составит 0,58а₀.
Таким образом, с
увеличением числа составляю­щих
портфеля риск уменьшается даже
при одинаковой диспер­сии
составляющих элементов. Однако прирост
действенности диверсификации
уменьшается. Соответствующая зависимость
изображена
на рис. 8.2.

Как
видим, наибольшее влияние увеличение
масштабов ди­версификации
оказывает на начальных стадиях, т.е. при
малых значениях
я. Например, в рамках рассмотренного
примера пе­реход
от одного вида бумаг к четырем сокращает
квадратиче­ское
отклонение на 50%, а от одного к восьми —
на 65%.

173

Рис.
8.2

Полученные
выше выводы в отношении тенденции
измене­ния
среднего квадратического отклонения
в зависимости от числа
составляющих при условии, когда дисперсии
составляю­щих
одинаковы, очевидно, справедливы и для
более общих слу­чаев.
Однако, зависимость этих параметров от
степени диверси­фикации
проявляется здесь не столь четко.

Посмотрим
теперь, как изменяются доход и величина
риска при
изменении структуры портфеля. Для этого
вернемся к фор­мулам
(8.2) и (8.3) и запишем их только для двух
видов бумаг (X
и
Y).
Такой
анализ вряд ли имеет практическое
значение. Однако
с его помощью наглядно демонстрируются
последствия “смешения”
ценных бумаг с различными доходностью
и дис­персией.
Для независимых доходов получим

D
= a²D‘
+ a²D_v, (8.5)

и
для зависимых доходов

D=
сРо²
+
а²
о²
+
2а
а г о о . (8.6)

** хх У
У ^х
У
*У ^х
У v”-^v/

Причем
а_у
=
1 — а_х.

В
этом случае среднее значение суммарного
дохода опреде­ляется
как

Л
=
a_xd_x
+
(1 – a_x)d_y. (8.7)

Пусть
d_y
> d_x
и
о_у
> о_х.
Очевидно,
что в силу этих условий рост
доли бумаг второго вида увеличивает
доходность портфе­ля.
Так, на основе (8.7) получим

Л
=
d_y
+
(d_y
–
d_x)a_y. (8.8)

Что
касается дисперсии дохода портфеля,
то, как это следу­ет
из (8.6), положение не столь однозначно и
зависит от знака

174

и
степени корреляции. В связи с этим
подробно рассмотрим три
ситуации: полная положительная корреляция
доходов (г = =
+1),
полная отрицательная корреляция (г =
-1), независи­мость доходов или нулевая
корреляция (г = 0).

В
первом случае увеличение дохода за счет
включения в порт­фель
бумаги вида У
помимо
X
сопровождается
ростом как дохо­да,
так и дисперсии. Для портфеля, содержащего
оба вида бумаг, квадратическое
отклонение находится в пределах о_х
< о < о (см.
рис. 8.3, где точка X
означает
портфель, состоящий только из
бумаг вида Л, а К— портфель из бумаг
вида Y).

Для
частного случая, когда о_х
=
о_у
=
а, получим по формуле (8.6)
D
=
а².
Иначе говоря, при полной положительной
корре­ляции
“смешение” инвестиций не окажет
никакого влияния на величину
дисперсии.

При
полной отрицательной корреляции доходов
динамика квадратического
отклонения доходов от портфеля более
слож­ная.
По мере движения от точки Л” к точке
К эта величина сна­чала
сокращается и доходит до нуля в точке
В,
затем
растет (см. рис.
8.4). Следует обратить внимание на то, что
при движении от
Л” до В
рост
дохода сопровождается уменьшением
риска (квадратического
отклонения).

В
последней из рассматриваемых ситуаций
квадратическое отклонение
при увеличении доли бумаги К проходит
точку ми­нимума,
равного а_т,
далее оно растет до о_у
(см.
рис. 8.5). (Проблема
определения состава портфеля, при
котором дости­гается
минимум дисперсии, обсуждается в
следующем парагра­фе.)

Совместим
теперь все три графика на одном (см. рис.
8.6.) Как
видим, все возможные варианты зависимости
“доход— С КО” находятся в треугольнике
XBY.

Рис.
8.3

Рис.
8.4

175

о
О
о_т
о_х о_у “О о_т
о_х о_у

Рис.
8.5 Рис.
8.6

Из
сказанного непосредственно следует,
что эффективность диверсификации
(в отношении сокращения риска) наблюдает­ся
только при отрицательной или, в крайнем
случае, нулевой корреляции.

ПРИМЕР
8.1. Портфель
должен
состоять
из
двух
видов
бумаг,
параметры
которых:
d_x
= 2;
о_х
= 0,8; d
= 3; о
= 1,1.

Доход
от
портфеля:
А
= 2а_х
+
За_у.
Таким
образом,
доход
в
за­висимости
от
величины
долей
находится
в
пределах
2 < А
< 3.

Дисперсия
суммы
дохода
составит:

D =
а^0,8²
+ а*1,1²
+ a^r^O.8
x
1,1.

Определим
доход
и
дисперсию
для
портфеля
с
долями,
рав­ными,
допустим,
0,3 и
0,7. Получим
по
формулам
(8.6) и
(8.7): D
= 0,651 +
0,37/-^ и
А
= 2,7. Таким
образом,
при
полной
поло­жительной
корреляции
D
=
1,021, при
полной
отрицательной
кор­реляции
D
= 0,281. В
итоге
с
вероятностью
95% можно
утвер­ждать,
что
суммарный
доход
находится
в
первом
случае
в
преде­лах
2,7 ±
2 х
^|^_t02^
«
2,7 ±
2,02; во
втором
—
он
определяется
пре­делами
2,7 ±
2 х
д/о,281
* 2,7 ±
1,06. При
нулевой
корреляции
до­ходов
искомые
пределы
составят
2,7 ±
2^/0,651 * 2,7 ±
1,64.

Продолжим
анализ с двумя бумагами и проследим,
как влия­ет
включение в портфель безрисковой (risk
free) инвестиции¹.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #

  11.06.201510.56 Mб26Borland C++ Builder.djvu

• #
• #
• #
• #
• #
• #
• #

Среднее абсолютное отклонение позволяет решить проблему, заключающуюся в том, что сумма отклонений от среднего равна нулю. Для этого при расчете среднего используется абсолютное значение отклонений.

Второй подход к расчету отклонений состоит в их возведении в квадрат.

Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии:

• Дисперсия определяется как среднее квадратов отклонений от среднего значения.
• Стандартное отклонение – это положительный квадратный корень дисперсии.

Далее обсуждается расчет и использования дисперсии и стандартного отклонения.

Дисперсия генеральной совокупности.

Если нам известен каждый элемент генеральной совокупности, мы можем вычислить дисперсию генеральной совокупности или просто дисперсию (англ. ‘population variance’).

Она обозначается символом (sigma^2)[сигма] и представляет собой среднее арифметическое квадратов отклонений от среднего значения.

Формула дисперсии генеральной совокупности.

Зная среднее значение μ, мы можем использовать Формулу 11 для вычисления суммы квадратов отклонений от среднего с учетом всех (N) элементов в генеральной совокупности, а затем для определения среднего квадратов отклонений путем деления этой суммы на (N).

Независимо от того, является ли отклонение от среднего положительным или отрицательным, возведение в квадрат этой разности дает положительное число.

Таким образом, дисперсия решает проблему отрицательных отклонений от среднего значения, устраняя их посредством операции возведения в квадрат этих отклонений.

---

Рассмотрим пример.

Прибыль в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год составляла 0.9%, 1.6% и 3.5% соответственно. Мы рассчитали среднюю прибыль в процентах от выручки как 2.0%.

Следовательно, дисперсия прибыли в процентах от выручки составляет:

(1/3)[(0.9 – 2.0)² + (1.6 – 2.0)² + (3.5 – 2.0)²]
= (1/3)(-1.1² + -0.4² + 1.5²)
= (1/3)(1.21 + 0.16 + 2.25) = (1/3)(3.62) = 1.21

Стандартное отклонение генеральной совокупности.

Поскольку дисперсия измеряется в квадратах, нам нужен способ вернуться к исходным единицам. Мы можем решить эту проблему, используя стандартное отклонение, т.е. квадратный корень из дисперсии.

Стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в той же единице измерения, что и наблюдения.

Формула стандартного отклонения генеральной совокупности.

Стандартное отклонение генеральной совокупности (или просто стандартное отклонение, а также среднеквадратическое отклонение, от англ. ‘population standard deviation’), определяемое как положительный квадратный корень из дисперсии генеральной совокупности, составляет:

Используя пример прибыли в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год, в соответствии с Формулой 12, мы вычислим дисперсию 1.21, а затем возьмем квадратный корень: ( sqrt{1.21} ) = 1.10.

Как дисперсия, так и стандартное отклонение являются примерами параметров распределения. В последующих чтениях мы введем понятие дисперсии и стандартного отклонения как меры риска.

Занимаясь инвестициями, мы часто не знаем среднего значения интересующей совокупности, обычно потому, что мы не можем практически идентифицировать или провести измерения для каждого элемента генеральной совокупности.

Поэтому мы рассчитываем среднее значение по генеральной совокупности и среднее выборки, взятой из совокупности, и вычисляем выборочную дисперсию или стандартное отклонение выборки, используя формулы, немного отличающиеся от Формул 11 и 12.

Мы обсудим эти вычисления далее.

Однако в инвестициях у нас иногда есть определенная группа, которую мы можем считать генеральной совокупностью. Для четко определенных групп наблюдений мы используем Формулы 11 и 12, как в следующем примере.

Пример расчета стандартного отклонения для генеральной совокупности.

В Таблице 20 представлен годовой оборот портфеля из 12 фондов акций США, которые вошли в список Forbes Magazine Honor Roll 2013 года.

Журнал Forbes ежегодно выбирает американские взаимные фонды, отвечающие определенным критериям для своего почетного списка Honor Roll.

Критериями являются:

• сохранение капитала (эффективность на медвежьем рынке),
• непрерывность управления (у фонда должен управлять менеджер непрерывно, в течение не менее 6 лет), диверсификация портфелей,
• доступность (дисквалификация фондов, которые закрыты для новых инвесторов), и
• долгосрочные показатели эффективности после уплаты налогов.

Оборачиваемость или оборот портфеля, показатель торговой активности, является меньшим значением из стоимости продаж или покупок за год, деленным на среднюю чистую стоимость активов за год. Количество и состав списка Forbes Honor Roll меняются из года в год.

Таблица 20. Оборот портфеля: взаимные фонды Forbes Honor Roll за 2013 год.

Фонд	Годовой оборот портфеля (%)
Bruce Fund (BRUFX)	10
CGM Focus Fund (CGMFX)	360
Hotchkis And Wiley Small Cap Value A Fund (HWSAX)	37
Aegis Value Fund (AVALX)	20
Delafield Fund (DEFIX)	49
Homestead Small Company Stock Fund (HSCSX)	1
Robeco Boston Partners Small Cap Value II Fund (BPSCX)	32
Hotchkis And Wiley Mid Cap Value A Fund (HWMAX)	72
T Rowe Price Small Cap Value Fund (PRSVX)	9
Guggenheim Mid Cap Value Fund Class A (SEVAX)	19
Wells Fargo Advantage Small Cap Value Fund (SSMVX)	16
Stratton Small-Cap Value Fund (STSCX)	11

Источник: Forbes (2013).

Основываясь на данных из таблицы 20, сделайте следующее:

1. Рассчитайте среднее по совокупности для оборота портфеля за период, используя данные для 12 фондов из Honor Roll.
2. Рассчитайте дисперсию и стандартное отклонение совокупности для оборота портфеля.
3. Объясните использование формул в этом примере.

---

Решение для части 1:

(mu) = (10 + 360 + 37 + 20 + 49 + 1 + 32 + 72 + 9 + 19 + 16 + 11)/12
= 636 /12 = 53%.

---

Решение для части 2:

Установив, что (mu) = 53%, мы можем вычислить дисперсию

( sigma^2 = { sum_{i=1}^{N} ( X_i – mu )^2 over N } ), сначала рассчитав числитель, а затем разделив результат на (N) = 12.

Числитель (сумма квадратов отклонений от среднего) равен:

(10 – 53)² + (360 – 53)² + (37 – 53)² + (20 – 53)² +
(49 – 53)² + (1 – 53)² + (32 – 53)² + (72 – 53)² +
(9 – 53)² + (19 – 53)² + (16 – 53)² + (11 – 53)² = 107,190

Таким образом,

( sigma^2 ) = 107,190/12 = 8,932.50.

Для расчета стандартного отклонения находим квадратный корень:

( sigma = sqrt{ 8,932.50 } ) = 94.51%.

Единицей измерения дисперсии является процент в квадрате, поэтому единицей измерения стандартного отклонения также является процент.

---

Решение для части 3:

Если генеральная совокупность четко определена как фонды Forbes Honor Roll за один конкретный год (2013 г.), и если под оборотом портфеля понимается конкретный одногодичный период, о котором отчитывается Forbes, то применение формул генеральной совокупности для дисперсии и стандартного отклонения уместно.

Результаты 8,932.50 и 94.51 представляют собой, соответственно, перекрестную дисперсию и стандартное отклонение годового оборота портфеля для фондов Forbes Honor Roll за 2013 год.

Фактически, мы не могли должным образом использовать фонды Honor Roll для оценки дисперсии оборота портфеля (например) любой другой по-разному определенной генеральной совокупности, потому что фонды Honor Roll не являются случайной выборкой из какой-либо большей генеральной совокупности взаимных фондов США.

Выборочная дисперсия.

Во многих случаях в управлении инвестициями подгруппа или выборка из генеральной совокупности – это все, что мы можем наблюдать. Когда мы имеем дело с выборками, сводные показатели называются статистикой.

Статистика, которая измеряет дисперсию по выборке, называется выборочной дисперсией или дисперсией выборки (англ. ‘sample variance’).

В приведенном ниже обсуждении обратите внимание на использование латинских букв вместо греческих для обозначения объема выборки.

Формула выборочной дисперсии.

Формула 13 предписывает нам предпринять следующие шаги для вычисления выборочной дисперсии:

1. Рассчитать выборочное среднее значение, ( overline X ).
2. Рассчитать квадратичное отклонение каждого наблюдения от среднего значения по выборке, ( ( X_i – overline X )^2 )
3. Найти сумму квадратов отклонений от среднего: ( sum_{i=1}^{n} ( X_i – overline X )^2 ).
4. Разделить сумму квадратов отклонений от среднего на ( (n – 1)).

Мы проиллюстрируем расчет выборочной дисперсии и выборочного стандартного отклонения на примере ниже.

Отличие выборочной дисперсии от дисперсии генеральной совокупности.

Мы используем обозначение ( s^2 ) для выборочной дисперсии, чтобы отличить ее от дисперсии генеральной совокупности ( sigma^2 ).

Формула для выборочной дисперсии почти такая же, как и для дисперсии генеральной совокупности, за исключением использования среднего значения выборки ( overline X ) вместо среднего значения генеральной совокупности μ и другого делителя.

В случае дисперсии генеральной совокупности мы делим числитель на размер совокупности (N). Однако для дисперсии выборки мы делим ее на размер выборки минус 1 или (n – 1). Используя (n – 1) (а не (n)) в качестве делителя мы улучшаем статистические свойства выборочной дисперсии.

В статистических терминах выборочная дисперсия, определенная в Формуле 13, является несмещенной оценкой (англ. ‘unbiased estimator ‘) дисперсии генеральной совокупности ( sigma^2 ).

Мы обсудим эту концепцию далее в чтении о выборке.

Величина (n – 1) также называется числом степеней свободы (англ. ‘number of degrees of freedom’) при оценке дисперсии генеральной совокупности.

Чтобы оценить дисперсию ( s^2 ), мы должны сначала вычислить среднее. После того как мы вычислили среднее значение выборки, существует только (n – 1) независимых отклонений от него.

Стандартное отклонение выборки.

Для стандартного отклонения генеральной совокупности мы аналогичным образом можем вычислить стандартное отклонение выборки, взяв квадратный корень из положительной дисперсии выборки.

Формула стандартного отклонения выборки.

Стандартное отклонение выборки (выборочное стандартное отклонение, выборочное среднеквадратическое отклонение, англ. ‘sample standard deviation’), обозначается символом (s) и рассчитывается следующим образом:

Чтобы рассчитать стандартное отклонение выборки, мы сначала вычисляем дисперсию выборки, используя приведенные выше шаги. Затем мы берем квадратный корень из выборочной дисперсии.

Пример, приведенный ниже, иллюстрирует расчет выборочной дисперсии и стандартного отклонения выборки для двух взаимных фондов, представленных ранее.

Пример расчета выборочной дисперсии и стандартного отклонения выборки.

После расчета геометрических и арифметических средних доходностей двух взаимных фондов в Примере (1) мы вычислили две меры дисперсии для этих фондов, размах и среднее абсолютное отклонение доходности (см.  Пример расчета размаха и среднего абсолютного отклонения для оценки риска).

Теперь мы вычислим выборочную дисперсию и стандартное отклонение выборки для доходности тех же двух фондов.

Таблица 15. Совокупная доходность двух взаимных фондов,
2008-2012 гг. (повтор).

Год	Фонд Selected American Shares (SLASX)	Фонд T. Rowe Price Equity Income (PRFDX)
2008	-39.44%	-35.75%
2009	31.64	25.62
2010	12.53	15.15
2011	-4.35	-0.72
2012	12.82	17.25

Источник: performance.morningstar.com.

На основании приведенных выше данных сделайте следующее:

1. Рассчитайте выборочную дисперсию доходности для (A) SLASX и (B) PRFDX.
2. Рассчитайте выборочное стандартное отклонение доходности для (A) SLASX и (B) PRFDX.
3. Сравните дисперсию доходности, измеренную стандартным отклонением доходности и средним абсолютным отклонением доходности для каждого из двух фондов.

---

Решение для части 1:

Чтобы вычислить выборочную дисперсию, мы используем Формулу 13 (значения отклонений приведены в процентах).

А. SLASX:

1. Среднее значение выборки:

( overline R ) = (-39.44 + 31.64 + 12.53 – 4.35 +12.82)/ 5 =
13.20/5 = 2.64%.

2. Квадратичные отклонения от среднего значения:

(-39.44 – 2.64)² = (-42.08)² = 1,770.73
(31.64 – 2.64)² = (29.00)² = 841.00
(12.53 – 2.64)² = (9.89)² = 97.81
(-4.35 – 2.64)² = (-6.99)² = 48.86
(12.82 – 2.64)² = (10.18)² = 103.63

3. Сумма квадратов отклонений от среднего составляет:

1,770.73 + 841.00 + 97.81 + 48.86 + 103.63 = 2,862.03.

4. Разделим сумму квадратов отклонений от среднего на (n – 1):

2,862.03 / (5 – 1) = 2,862.03 / 4 = 715.51

B. PRFDX:

1. Среднее значение выборки:

( overline R ) = (-35.75 + 25.62 + 15.15 – 0.72 + 17.25)/5 = 21.55/5 = 4.31%.

2. Квадратичные отклонения от среднего значения:

(-35.75 – 4.31)² = (-40.06)² = 1,604.80
(25.62 – 4.31)² = (21.31)² = 454.12
(15.15 – 4.31)² = (10.84)² = 117.51
(-0.72 – 4.31)² = (-5.03)² = 25.30
(17.25 – 4.31)² = (12.94)² = 167.44

3. Сумма квадратов отклонений от среднего составляет:

1,604.80 + 454.12 + 117.51 + 25.30 + 167.44 = 2,369.17.

4. Разделим сумму квадратов отклонений от среднего на ((n – 1)):

2,369.17/4 = 592.29

---

Решение для части 2:

Чтобы найти стандартное отклонение, мы берем положительный квадратный корень из дисперсии.

---

Решение для части 3:

Таблица 21 суммирует результаты части 2 для стандартного отклонения и включает результаты для MAD из Примера расчета размаха и среднего абсолютного отклонения для оценки риска.

Таблица 21. Два взаимных фонда: сравнение стандартного отклонения и среднего абсолютного отклонения (MAD).

Фонд	Стандартное отклонение (%)	Среднее абсолютное отклонение (%)
SLASX	26.7	19.6
PRFDX	24.3	18.0

Обратите внимание, что среднее абсолютное отклонение меньше стандартного отклонения. Среднее абсолютное отклонение всегда будет меньше или равно стандартному отклонению, потому что стандартное отклонение придает больший вес большим отклонениям, чем маленьким (помните, что отклонения возводятся в квадрат).

Поскольку стандартное отклонение является мерой дисперсии относительно среднего арифметического, мы обычно представляем  среднее арифметическое и стандартное отклонение вместе при анализе данных.

Когда мы имеем дело с данными, которые представляют собой временной ряд процентных изменений, представление геометрического среднего, представляющего собой сложную ставку скорости роста, также очень полезно.

---

В Таблице 22 представлены исторические геометрические и арифметические средние доходности, а также историческое стандартное отклонение доходности для годовой и месячной доходности S&P 500.

Мы представляем эту статистику для номинальной (без поправки на инфляцию) доходности, чтобы мы могли наблюдать первоначальные величины доходности.

Таблица 22. Доходность рынка ценных бумаг: средние значения и стандартные отклонения.

Ставка доходности	Геометрическое среднее (%)	Среднее арифметическое (%)	Стандартное отклонение
S&P 500 (Годовая)	9.84	11.82	20.18
S&P 500 (Месячная)	0.79	0.94	5.50

Источник: Ibbotson.

Дисперсия (вариация) | Variance

В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.

Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:

где k_i – доходность ценной бумаги или актива при i-ом варианте исхода событий;

— ожидаемая доходность ценной бумаги или актива;

p_i – вероятность i-го варианта исхода событий.

В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:

где k_i – i-ое значение доходности ценной бумаги;

— средняя доходность ценной бумаги;

n – количество наблюдений.

Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:

Интерпретации дисперсии

Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.

Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.

Пример расчета

Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.

Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.

_А = 7*0,05+15*0,2+18*0,5+24*0,2+32*0,05 = 18,75%

_Б = -24*0,05+8*0,2+20*0,5+31*0,2+57*0,05 = 19,45%

В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.

σ 2 _А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%

σ 2 _Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%

Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.

Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.

Средняя доходность акции составит 5,784%.

= (5,78+12,33-7,21+8,25+9,77)/5 = 5,784%

Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.

σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%

Дисперсия как мера финансового инвестиционного риска. Оценка дисперсии и среднеквадратического отклонения доходности ценных бумаг.

В статистике дисперсия или вариация является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.

Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:

где k_i – доходность ценной бумаги или актива при i-ом варианте исхода событий;

— ожидаемая доходность ценной бумаги или актива;

p_i – вероятность i-го варианта исхода событий.

В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:

где k_i – i-ое значение доходности ценной бумаги;

— средняя доходность ценной бумаги;

n – количество наблюдений.

Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:

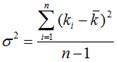
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.

Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.

Под риском можно понимать вероятность возникновения каких-либо отклонений от ожидаемого события. Основополагающими мерами риска финансового актива являются такие показатели, как стандартное отклонение (σ) и дисперсия (D = σ2) сто доходности. В качестве синонима понятия «стандартное отклонение» используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива отражают степень возможного разброса его фактической доходности вокруг его средней (наиболее вероятной) доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива.

Доходность актива на рассматриваемом интервале определяется следующим образом:

где St-1 – стоимость актива в начале интервала наблюдения; St – стоимость актива в конце интервала наблюдения.

Пусть имеются значения доходности акции за п равных интервалов наблюдения. За первый интервал она составила величину R1, за второй – R2 и т.д., за п-й интервал – Rn

Средняя доходность актива за наблюдаемый период (R) рассчитывается по формуле

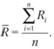
Дисперсия доходности актива определяется как мера разброса наблюдаемой доходности (в процентах) от ее математического ожидания (средней величины). Формула генеральной дисперсии имеет вид

В случае если количество наблюдений незначительно (меньше 30), то для получения несмещенной оценки рекомендуется использовать так называемую исправленную дисперсию:

Показателем, характеризующим относительный уровень риска финансового актива, является стандартное отклонение его доходности от ожидаемой (средней за период):

При этом оценка допустимого уровня стандартного отклонения является субъективной и характеризует готовность инвестора принимать риск с учетом возможной доходности финансового актива.

§ 4.2. Диверсификация инвестиций и дисперсия дохода

Определим теперь, что дает диверсификация для уменьшения риска, и выявим условия, когда эта цель достигается. В качестве объекта анализа примем некоторый абстрактный портфель ценных бумаг (далее для краткости — портфель). Такой выбор объясняется методологическими преимуществами — в этом случае проще выявить зависимости между основными переменными. Однако многие из полученных результатов без большой натяжки можно распространить и на производственные инвестиции.

В § 4.1 отмечалось, что в качестве измерителя риска в долгосрочных финансовых операциях широко распространена такая мера, как дисперсия дохода во времени. Диверсификация портфеля при правильном ее применении приводит к уменьшению этой дисперсии при всех прочих равных условиях. Диверсификация базируется на простой гипотезе. Если каждая компонента портфеля (в рассматриваемой задаче — вид ценной бумаги) характеризуется некоторой дисперсией дохода, то доход от портфеля имеет дисперсию, определяемую его составом. Таким образом, изменяя состав портфеля, можно менять суммарную дисперсию дохода, а в некоторых случаях свести ее к минимуму.

Итак, пусть имеется портфель из п видов ценных бумаг. Доход от одной бумаги вида i составляет величину d_i. Суммарный доход А равен:

(4.1)

Если d_i представляет собой средний доход от бумаги вида i, то величина А характеризует средний доход от портфеля бумаг в целом.

Для начала положим, что показатели доходов различных видов бумаг являются статистически независимыми величинами (иначе говоря, не коррелируют между собой). Дисперсия дохода портфеля (обозначим ее D) в этом случае находится как

(4.2)

где D_i — дисперсия дохода от бумаги вида i.

Для упрощения, которое нисколько не повлияет на результаты дальнейших рассуждений, перейдем от абсолютного измерения количества ценных бумаг к относительному. Пусть теперь a_i характеризует долю в портфеле бумаги вида i. Соответственно 0 a_i 1; a_i = 1.

Для зависимых в статистическом смысле показателей дохода отдельных бумаг дисперсию суммарного дохода находим следующим образом 19 :

(4.3)

где D_i — дисперсия дохода от бумаги вида i;

r_ij — коэффициент корреляции дохода от бумаг вида i и j;

и — среднее квадратическое отклонение доходау бумаг вида i и j.

Коэффициент корреляции двух случайных переменных х и у 20 , как известно, определяется по формуле:

, (4.4)

где — средние (в нашем случае средние доходы двух видов бумаг).

Для расчетов часто применяется следующая рабочая формула:

.

Поскольку коэффициент корреляции может быть как положительной, так и отрицательной величиной, то при положительной корреляции дисперсия суммарного дохода увеличивается, при отрицательной — сокращается. В самом деле, при заметной отрицательной корреляции положительные отклонения от среднего дохода одних бумаг погашаются отрицательными отклонениями у других. И наоборот, при положительной корреляции отклонения суммируются, что увеличивает общую дисперсию и риск.

Проследим теперь, каково влияние масштаба диверсификации на размер риска. Под масштабом диверсификации будем понимать количество объектов, возможных для инвестирования (количество видов ценных бумаг). Обратимся к условному примеру, который позволяет наиболее отчетливо выделить влияние указанного фактора. Итак, пусть портфель состоит из бумаг различного вида, но имеющих одинаковую дисперсию дохода . Удельные веса в портфеле каждого вида бумаг также одинаковы, а общая сумма вложений равна 1. Положим, что показатели доходности у отдельных видов бумаг статистически независимы, т. е. применима формула (4.2). В этих условиях для оценки величины среднего квадратического отклонения дохода портфеля получим:

,

где п — количество видов ценных бумаг.

Воспользуемся приведенной формулой и определим дисперсию дохода для портфеля, состоящего из двух и трех видов бумаг. Так, для двух бумаг имеем

.

Для трех видов бумаг квадратическое отклонение портфеля составит 0,58₀. Таким образом, с увеличением числа составляющих портфеля риск уменьшается даже при одинаковой дисперсии составляющих элементов, однако действенность диверсификации снижается. Соответствующая зависимость изображена на рис. 4.2.

Увеличение масштабов диверсификации оказывает наибольшее влияние на начальных стадиях — при малых значениях n. Например, в рамках рассмотренного примера переход от одного вида бумаг к четырем сокращает квадратическое отклонение на 50%, а от одного к восьми — на 65%.

Полученные выше выводы в отношении тенденции изменения среднего квадратического отклонения в зависимости от числа составляющих при условии, когда дисперсии составляю-

щих одинаковы, справедливы и для более общих случаев. Однако зависимость этого параметра от степени диверсификации проявляется здесь не столь четко.

Посмотрим теперь, как изменяются доход и величина риска при изменении структуры портфеля. Для этого вернемся к формулам (4.2) и (4.3) и запишем их только для двух видов бумаг (X и Y). Такой анализ вряд ли имеет практическое значение. Однако с его помощью наглядно демонстрируются последствия «смешения» ценных бумаг с различными доходностью и дисперсией. Для независимых доходов получим:

(4.5)

и для зависимых доходов

(4.6)

В этом случае среднее значение суммарного дохода определяется как

Положим, что d_y > d_x и . Тогда увеличение доли бумаг второго вида увеличивает доходность портфеля. Так, на основе (4.7) получим

Что касается дисперсии, то, как следует из (4.6), положение не столь однозначно и зависит от знака и степени корреляции. В связи с этим подробно рассмотрим три ситуации:

полная положительная корреляция доходов (r_xy = +1),

независимость доходов или нулевая корреляция (r_ху = 0).

В первом случае увеличение дохода за счет включения в портфель бумаги вида Y помимо X сопровождается ростом как дохода, так и дисперсии. Для портфеля, содержащего оба вида бумаг, квадратическое отклонение находится в пределах (рис. 4.3).

Для частного случая, когда , получим по формуле (4.6)D =. Иначе говоря, «смешение» инвестиций здесь не окажет никакого влияния на величину дисперсии.

При полной отрицательной корреляции доходов динамика квадратического отклонения доходов от портфеля более сложная. По мере движения от точки X к точке Y эта величина сначала сокращается и доходит до нуля в точке B, затем растет (рис. 4.4).

В последней из рассматриваемых ситуаций (r_ху = 0) квадратическое отклонение при увеличении доли бумаги Y проходит точку минимума, равного , далее оно растет до(рис. 4.5).

Совместим теперь все три графика на одном (рис. 4.6). Как видим, все возможные варианты зависимости «доход — среднее квадратическое отклонение» находятся в треугольнике XBY.

Из сказанного непосредственно следует, что эффективность диверсификации (в отношении сокращения риска) наблюдается только при отрицательной или, в крайнем случае, нулевой корреляции.

Портфель должен состоять из двух видов бумаг, параметры которых: d_x = 2; = 0,8;d_y = 3; = 1,1.

Доход от портфеля: А = 2а_х + 3а_у . Таким образом, доход в зависимости от величины долей находится в пределах 2А3 .

Дисперсия суммы дохода составит:

.

Определим доход и дисперсию для портфеля с долями, равными, допустим, 0,3 и 0,7. Получим по формулам (4.5) и (4.6):

Таким образом, при полной положительной корреляции D = 0,854, при полной отрицательной корреляции D = 0,484 . В итоге с вероятностью 95% можно утверждать, что суммарный доход находится в первом случае в пределах

во втором он определяется пределами

.

При нулевой корреляции доходов пределы составят

.

Продолжим анализ с двумя бумагами и проследим, как влияет включение в портфель безрисковой (risk free) инвестиции 21 . Для этого заменим в портфеле бумагу Y с параметрами d_y, на бумагу с такой же доходностью, но с нулевой дисперсией. Доходность портфеля от такой замены, разумеется, не изменится. Что же касается дисперсии, то она теперь составит:

.

Дисперсия и среднее квадратическое отклонение дохода портфеля теперь зависят от удельного веса безрисковой составляющей:

(4.9)

Таким образом, «разбавление» портфеля безрисковой бумагой снижает риск портфеля в целом, а квадратическое отклонение дохода портфеля определяется убывающей линейной функцией доли безрисковой бумаги. Если d_x > d_y (в противном случае проблема выбора портфеля отпадает — он должен состоять только из безрисковых бумаг), то доход от портфеля по мере увеличения доли безрисковой бумаги уменьшается от d_x до d_y, а величина квадратического отклонения сокращается от до 0 (рис. 4.7). И наоборот, рост доли рисковой бумаги увеличивает как риск, так и доход.

Последнее утверждение для портфеля, состоящего из двух видов бумаг, иллюстрируется уравнением (4.10):

В свою очередь, на основе (4.9) находим

.

В итоге получим интересное соотношение

. (4.11)

Дробь в приведенном выражении иногда называют рыночной ценой риска. Если эта величина равна, скажем, 0,5, то при росте квадратического отклонения на 1% доход увеличится на 0,5%.

Источники: http://allfi.biz/financialmanagement/RiskAndReturns/dispersija.php, http://infopedia.su/15x1cfe.html, http://studfiles.net/preview/2214105/page:17/

Дисперсия прибыли Разница между вашей фактической прибылью за данный период и вашей прогнозируемой прибылью. Существует несколько конкретных форм дисперсии прибыли, но простой расчет состоит в том, чтобы вычесть прогнозируемую сумму из ваших фактических результатов.

Пример расчета

Предположим, что прибыль вашего бизнеса в данном квартале составит 200 000 долларов. Фактическая прибыль составила 225 000 долларов. В этом случае вы вычитаете 200 000 долларов США из 225 000 долларов США, чтобы определить отклонение прибыли в 25 000 долларов США. Если бы цифры были перевернуты, и вы прогнозировали 225 000 долларов, но получили 200 000 долларов, вы бы получили отрицательная разница прибыли 25 000 долларов.

Типы дисперсии прибыли

Компании обычно сообщают о трех различных типах прибыли в отчете о прибылях и убытках: валовая прибыль, операционная прибыль и чистая прибыль. В то время как чистая прибыль равна вашим итоговым результатам после того, как все учтено, распознавание отклонения прибыли на каждом уровне позволяет вам определить области силы или слабости.

Чтобы рассчитать дисперсию валовой прибыли, вы бы вычесть вашу прогнозируемую валовую прибыль из вашей фактической валовой прибыли, что равняется периодическим продажам за вычетом затрат на проданные товары. Для операционной дисперсии вычтите прогнозируемую операционную прибыль из фактической операционной прибыли, которая равна выручке за вычетом всех расходов и операционных расходов. Для отклонения чистой прибыли вычтите прогнозируемую чистую прибыль из фактической чистой прибыли, которая равна всем регулярным и нерегулярным доходам за вычетом всех регулярных и нерегулярных расходов.

Отклонения от прибыли

Любой расчет дисперсии, который дает положительный результат благоприятентогда как отрицательная дисперсия или прибыль ниже прогнозируемой является неблагоприятной. Если у вас есть отрицательная разница валовой прибыли, ваш объем продаж может не достигнуть целевого уровня, или вы получили неожиданно высокий уровень COGS, Отрицательное рабочее отклонение может быть вызвано теми же причинами или неожиданно высоким рабочим отклонением. Отрицательное отклонение чистой прибыли является обычным явлением, когда у вас есть нерегулярные действия, такие как большие судебные издержки.

подсказки

• Усовершенствованный маркетинг и мерчендайзинг могут способствовать положительному отклонению доходов и прибыли. Переговоры о снижении COGS или ставок операционных расходов являются другими стратегиями для оптимизации прибыли.