Дисперсия и среднее квадратичное отклонение числового ряда.

Дисперсия и Среднее квадратичное отклонение
числового ряда

Задача
Дисперсией ряда чисел называется среднее арифметическое
Оля и Гуля проводили подготовку к соревнованиям по стрельбе из лука. Спортсменки произвели по 7 серий выстрелов. Каждая серия состояла из 12 выстрелов. Получили следующие данные:

Задача
Дисперсией ряда чисел называется среднее арифметическое
Оля и Гуля проводили подготовку к соревнованиям по стрельбе из лука. Спортсменки произвели по 7 серий выстрелов. Каждая серия состояла из 12 выстрелов. Получили следующие данные:
Оля: 11, 11, 12, 11, 9, 11, 12.

Задача
Дисперсией ряда чисел называется среднее арифметическое
Оля и Гуля проводили подготовку к соревнованиям по стрельбе из лука. Спортсменки произвели по 7 серий выстрелов. Каждая серия состояла из 12 выстрелов. Получили следующие данные:
Оля: 11, 11, 12, 11, 9, 11, 12.
Гуля: 12, 10, 9, 12, 11, 12, 11.

Задача
Дисперсией ряда чисел называется среднее арифметическое
По итогам полученных данных подведены
результаты попадания в цель.
Кто лучше готов к соревнованиям?
Оля: 11, 11, 12, 11, 9, 11, 12.
Гуля: 12, 10, 9, 12, 11, 12, 11.

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ряда
Дисперсией ряда чисел называется среднее арифметическое
Найдём среднее арифметическое результатов для каждого спортсмена:
Оля
Гуля

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ряда
Дисперсией ряда чисел называется среднее арифметическое
Найдём среднее арифметическое результатов для каждого спортсмена:
Оля
Гуля

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ряда
Дисперсией ряда чисел называется среднее арифметическое
Найдём среднее арифметическое результатов для каждого спортсмена:
Оля
Гуля

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ряда
Дисперсией ряда чисел называется среднее арифметическое
Найдём среднее арифметическое результатов для каждого спортсмена:
Значения одинаковы. Кто лучше готов к соревнованиям?
Оля
Гуля

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Вычислим дисперсию результатов для каждого спортсмена:

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Вычислим дисперсию результатов для каждого спортсмена:
Дисперсией ряда чисел называется
среднее арифметическое
квадратов их отклонений от среднего арифметического этого ряда.

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Вычислим дисперсию результатов для каждого спортсмена:

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Вычислим дисперсию результатов для каждого спортсмена:

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Дисперсии данных результатов:
DОли = 0,86 DГули = 1,14

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Дисперсии данных результатов:
DОли = 0,86 DГули = 1,14
Разброс данных у Оли меньше − это свидетельствует о
её лучшей подготовке.

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Дисперсии данных результатов:
DОли = 0,86 DГули = 1,14
Разброс данных у Оли меньше − это свидетельствует о
её лучшей подготовке. Данный пример демонстрирует,
что при равных средних арифметических значениях,
именно дисперсия позволила выявить наименьший разброс данных среди результатов.

ДИСПЕРСИЯ ряда
Дисперсией ряда чисел называется среднее арифметическое
Дисперсии данных результатов:
DОли = 0,86 DГули = 1,14
Разброс данных у Оли меньше − это свидетельствует о
её лучшей подготовке. Данный пример демонстрирует,
что при равных средних арифметических значениях,
именно дисперсия позволила выявить наименьший разброс данных среди результатов.
Оля лучше готова и показала более стабильный результат.

Среднее квадратичное отклонение ряда
Дисперсией ряда чисел называется среднее арифметическое
Вычислим среднее квадратичное отклонение
результатов для каждого спортсмена:

Среднее квадратичное отклонение ряда
Дисперсией ряда чисел называется среднее арифметическое
Вычислим среднее квадратичное отклонение
результатов для каждого спортсмена:
Средним квадратичным отклонением числового ряда называют квадратный корень из дисперсии этого ряда.

Среднее квадратичное отклонение ряда
Вычислим среднее квадратичное отклонение
результатов для каждого спортсмена:

Среднее квадратичное отклонение ряда
Вычислим среднее квадратичное отклонение
результатов для каждого спортсмена:
Как найти дисперсию?
Спасибо за ваши закладки и рекомендации
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Загрузить PDF
Загрузить PDF
Дисперсия случайной величины является мерой разброса значений этой величины. Малая дисперсия означает, что значения сгруппированы близко друг к другу. Большая дисперсия свидетельствует о сильном разбросе значений. Понятие дисперсии случайной величины применяется в статистике. Например, если сравнить дисперсию значений двух величин (таких как результаты наблюдений за пациентами мужского и женского пола), можно проверить значимость некоторой переменной.[1]
Также дисперсия используется при построении статистических моделей, так как малая дисперсия может быть признаком того, что вы чрезмерно подгоняете значения.[2]
-

1
Запишите значения выборки. В большинстве случаев статистикам доступны только выборки определенных генеральных совокупностей. Например, как правило, статистики не анализируют расходы на содержание совокупности всех автомобилей в России – они анализируют случайную выборку из нескольких тысяч автомобилей. Такая выборка поможет определить средние расходы на автомобиль, но, скорее всего, полученное значение будет далеко от реального.
- Например, проанализируем количество булочек, проданных в кафе за 6 дней, взятых в случайном порядке. Выборка имеет следующий вид: 17, 15, 23, 7, 9, 13. Это выборка, а не совокупность, потому что у нас нет данных о проданных булочках за каждый день работы кафе.
- Если вам дана совокупность, а не выборка значений, перейдите к следующему разделу.
-

2
Запишите формулу для вычисления дисперсии выборки. Дисперсия является мерой разброса значений некоторой величины. Чем ближе значение дисперсии к нулю, тем ближе значения сгруппированы друг к другу. Работая с выборкой значений, используйте следующую формулу для вычисления дисперсии:[3]
-

3
Вычислите среднее значение выборки. Оно обозначается как x̅.[4]
Среднее значение выборки вычисляется как обычное среднее арифметическое: сложите все значения в выборке, а затем полученный результат разделите на количество значений в выборке.- В нашем примере сложите значения в выборке: 15 + 17 + 23 + 7 + 9 + 13 = 84
Теперь результат разделите на количество значений в выборке (в нашем примере их 6): 84 ÷ 6 = 14.
Выборочное среднее x̅ = 14. - Выборочное среднее – это центральное значение, вокруг которого распределены значения в выборке. Если значения в выборке группируются вокруг выборочного среднего, то дисперсия мала; в противном случае дисперсия велика.
- В нашем примере сложите значения в выборке: 15 + 17 + 23 + 7 + 9 + 13 = 84
-

4
Вычтите выборочное среднее из каждого значения в выборке. Теперь вычислите разность
– x̅, где
– каждое значение в выборке. Каждый полученный результат свидетельствует о мере отклонения конкретного значения от выборочного среднего, то есть как далеко это значение находится от среднего значения выборки.[5]
-

5
Возведите в квадрат каждый полученный результат. Как отмечалось выше, сумма разностей
– x̅ должна быть равна нулю. Это означает, что средняя дисперсия всегда равна нулю, что не дает никакого представления о разбросе значений некоторой величины. Для решения этой проблемы возведите в квадрат каждую разность
– x̅. Это приведет к тому, что вы получите только положительные числа, которые при сложении никогда не дадут 0.[6]
-

6
-

7
Полученный результат разделите на n – 1, где n – количество значений в выборке. Некоторое время назад для вычисления дисперсии выборки статистики делили результат просто на n; в этом случае вы получите среднее значение квадрата дисперсии, которое идеально подходит для описания дисперсии данной выборки. Но помните, что любая выборка – это лишь небольшая часть генеральной совокупности значений. Если взять другую выборку и выполнить такие же вычисления, вы получите другой результат. Как выяснилось, деление на n – 1 (а не просто на n) дает более точную оценку дисперсии генеральной совокупности, в чем вы и заинтересованы. Деление на n – 1 стало общепринятым, поэтому оно включено в формулу для вычисления дисперсии выборки.[7]
- В нашем примере выборка включает 6 значений, то есть n = 6.
Дисперсия выборки =33,2
- В нашем примере выборка включает 6 значений, то есть n = 6.
-

8
Отличие дисперсии от стандартного отклонения. Заметьте, что в формуле присутствует показатель степени, поэтому дисперсия измеряется в квадратных единицах измерения анализируемой величины. Иногда такой величиной довольно сложно оперировать; в таких случаях пользуются стандартным отклонением, которое равно квадратному корню из дисперсии. Именно поэтому дисперсия выборки обозначается как
, а стандартное отклонение выборки – как
.
- В нашем примере стандартное отклонение выборки: s = √33,2 = 5,76.
Реклама
-

1
Проанализируйте некоторую совокупность значений. Совокупность включает в себя все значения рассматриваемой величины. Например, если вы изучаете возраст жителей Ленинградской области, то совокупность включает возраст всех жителей этой области. В случае работы с совокупностью рекомендуется создать таблицу и внести в нее значения совокупности. Рассмотрим следующий пример:
-

2
Запишите формулу для вычисления дисперсии генеральной совокупности. Так как в совокупность входят все значения некоторой величины, то приведенная ниже формула позволяет получить точное значение дисперсии совокупности. Для того чтобы отличить дисперсию совокупности от дисперсии выборки (значение которой является лишь оценочным), статистики используют различные переменные: [8]
-

3
Вычислите среднее значение совокупности. При работе с генеральной совокупностью ее среднее значение обозначается как μ (мю). Среднее значение совокупности вычисляется как обычное среднее арифметическое: сложите все значения в генеральной совокупности, а затем полученный результат разделите на количество значений в генеральной совокупности.
- Имейте в виду, что средние величины не всегда вычисляются как среднее арифметическое.
- В нашем примере среднее значение совокупности: μ =
= 10,5
-

4
Вычтите среднее значение совокупности из каждого значения в генеральной совокупности. Чем ближе значение разности к нулю, тем ближе конкретное значение к среднему значению совокупности. Найдите разность между каждым значением в совокупности и ее средним значением, и вы получите первое представление о распределении значений.
- В нашем примере:
– μ = 5 – 10,5 = -5,5
– μ = 5 – 10,5 = -5,5
– μ = 8 – 10,5 = -2,5
– μ = 12 – 10,5 = 1,5
– μ = 15 – 10,5 = 4,5
– μ = 18 – 10,5 = 7,5
- В нашем примере:
-

5
Возведите в квадрат каждый полученный результат. Значения разностей будут как положительными, так и отрицательными; если нанести эти значения на числовую прямую, то они будут лежать справа и слева от среднего значения совокупности. Это не годится для вычисления дисперсии, так как положительные и отрицательные числа компенсируют друг друга. Поэтому возведите в квадрат каждую разность, чтобы получить исключительно положительные числа.
- В нашем примере:
(– μ)
для каждого значения совокупности (от i = 1 до i = 6):
(-5,5)= 30,25
(-5,5)= 30,25
(-2,5)= 6,25
(1,5)= 2,25
(4,5)= 20,25
(7,5)= 56,25
- В нашем примере:
-

6
Найдите среднее значение полученных результатов. Вы нашли, как далеко каждое значение совокупности расположено от ее среднего значения. Найдите среднее значение суммы квадратов разностей, поделив ее на количество значений в генеральной совокупности.
- В нашем примере:
Дисперсия совокупности =24,25
- В нашем примере:
-

7
Соотнесите это решение с формулой. Если вы не поняли, как приведенное выше решение соотносится с формулой, ниже представлено объяснение решения:
Реклама
Советы
- Дисперсию довольно сложно интерпретировать, поэтому в большинстве случаев она вычисляется как промежуточная величина, которая необходима для нахождения стандартного отклонения.
- При вычислении дисперсии выборки деление на n-1, а не просто на n, называется коррекцией Бесселя. Дисперсия выборки представляет собой только оценочное значение дисперсии генеральной совокупности, при этом выборочное среднее смещено, чтобы соответствовать этому оценочному значению. Коррекция Бесселя устраняет такое смещение.[9]
Это связано с тем, что при анализе n – 1 значения использование n-го значения уже ограничено, так как только определенные значения приводят к выборочному среднему (x̅), которое используется в формуле для вычисления дисперсии.[10]
Реклама
Об этой статье
Эту страницу просматривали 121 964 раза.
Была ли эта статья полезной?
Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения.
Основными обобщающими
показателями вариации в статистике
являются дисперсии и среднее квадратическое
отклонение.
Дисперсия
– это средняя арифметическая квадратов
отклонений каждого значения признака
от общей средней. Дисперсия обычно
называется средним квадратом отклонений
и обозначается
![]() .
.
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:
![]() —дисперсия
—дисперсия
невзвешенная (простая);
![]() —дисперсия
—дисперсия
взвешенная.
Среднее квадратическое
отклонение представляет собой корень
квадратный из дисперсии и обозначается
S:
![]() —среднее
—среднее
квадратическое отклонение невзвешенное;
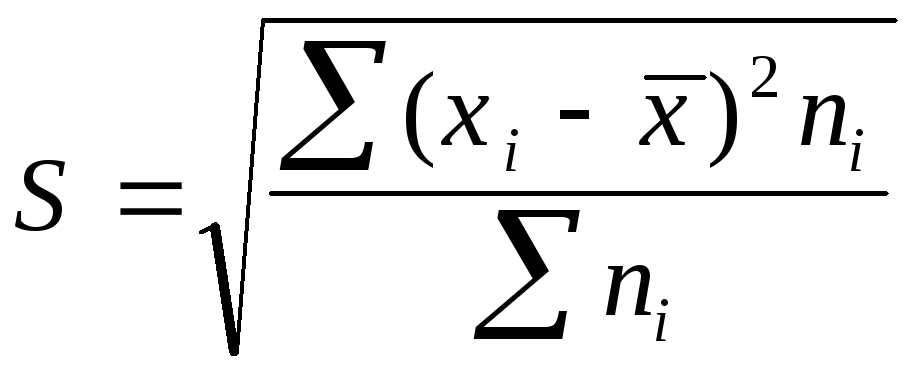 —среднее
—среднее
квадратическое отклонение взвешенное.
Среднее
квадратическое отклонение
– это обобщающая характеристика абсолютных
размеров вариации признака в совокупности.
Выражается оно в тех же единицах
измерения, что и признак (в метрах,
тоннах, процентах, гектарах и т.д.).
Среднее квадратическое
отклонение является мерилом надежности
средней. Чем меньше среднее квадратическое
отклонение, тем лучше средняя арифметическая
отражает собой всю представляемую
совокупность.
Вычислению среднего
квадратического отклонения предшествует
расчет дисперсии.
Порядок расчета
дисперсии взвешенную:
1) определяют
среднюю арифметическую взвешенную
![]() ;
;
2) определяются
отклонения вариант от средней
![]() ;
;
3) возводят в квадрат
отклонение каждой варианты от средней
![]() ;
;
4) умножают квадраты
отклонений на веса (частоты)
![]() ;
;
5) суммируют
полученные произведения
![]() ;
;
6) Полученную сумму
делят на сумму весов
 .
.
Пример 3.
Таблица 6.3.
|
Произведено ( |
Число |
|
|
|
|
|
8 |
7 |
56 |
-2 |
4 |
28 |
|
9 |
10 |
90 |
-1 |
1 |
10 |
|
10 |
15 |
150 |
0 |
0 |
0 |
|
11 |
12 |
132 |
1 |
1 |
12 |
|
12 |
6 |
72 |
2 |
4 |
24 |
|
ИТОГО |
50 |
500 |
74 |
Исчислим среднюю
арифметическую взвешенную:
![]() шт.
шт.
Значения отклонений
от средней и их квадратов представлены
в таблице 6.3. Определим дисперсию:
![]() =1,48
=1,48
Среднее квадратическое
отклонение будет равно:
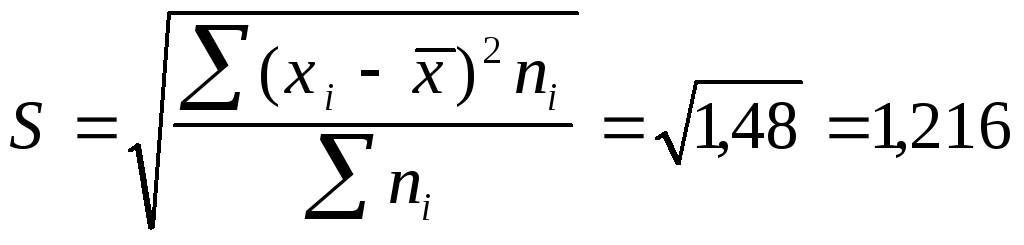 шт.
шт.
Если исходные
данные представлены в виде интервального
ряда распределения, то сначала надо
определить дискретное значение признака,
а далее применить тот же метод, что
изложен выше.
Пример 4.
Покажем расчет
дисперсии для интервального ряда на
данных о распределении посевной площади
колхоза по урожайности пшеницы:
Таблица 6.4
|
Урожайность |
Посевная |
|
|
|
|
|
|
14 |
100 |
15 |
1500 |
-3,4 |
11,56 |
1156 |
|
16 |
300 |
17 |
5100 |
-1,4 |
1,96 |
588 |
|
18 |
400 |
19 |
7600 |
0,6 |
0,36 |
144 |
|
20 |
200 |
21 |
4200 |
2,6 |
6,76 |
1352 |
|
ИТОГО |
1000 |
18400 |
3240 |
Средняя арифметическая
равна:
![]() ц с 1га.
ц с 1га.
Исчислим дисперсию:
![]()
Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.
Техника вычисления
дисперсии сложна, а при больших значениях
вариант и частот может быть громоздкой.
Расчеты можно упростить, используя
свойства дисперсии.
Свойства
дисперсии.
-
Уменьшение или
увеличение весов (частот) варьирующего
признака в определенное число раз
дисперсии не изменяет. -
Уменьшение или
увеличение каждого значения признака
на одну и ту же постоянную величину А
дисперсии не изменяет. -
Уменьшение или
увеличение каждого значения признака
в какое-то число раз к соответственно
уменьшает или увеличивает дисперсию
в
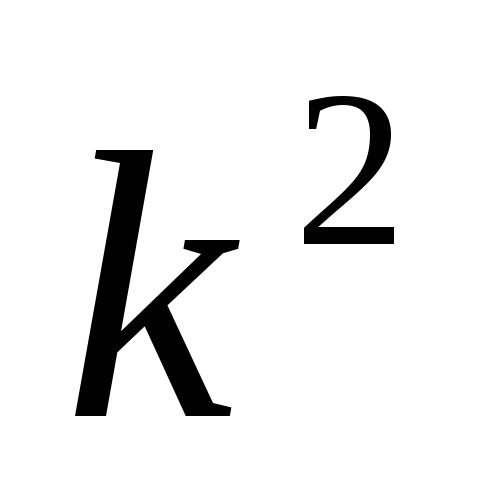 раз, а среднее квадратическое отклонение
раз, а среднее квадратическое отклонение
– в к раз. -
Дисперсия признака
относительно произвольной величины
всегда больше дисперсии относительно
средней арифметической на квадрат
разности между средней и произвольной
величиной:
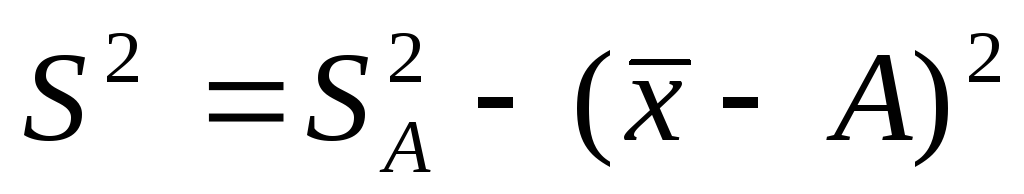 .
.
Если А равна нулю, то приходим к
следующему равенству: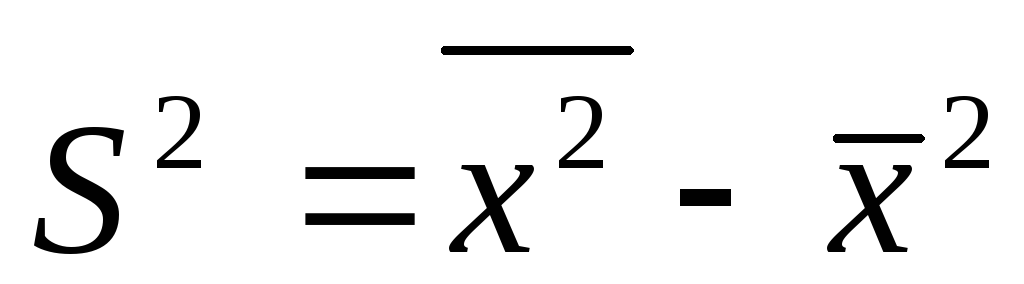 ,
,
т.е. дисперсия признака равна разности
между средним квадратом значений
признака и квадратом средней.
Каждое свойство
при расчете дисперсии может быть
применено самостоятельно или в сочетании
с другими.
Порядок расчета
дисперсии простой:
1) определяют
среднюю арифметическую
![]() ;
;
2) возводят в квадрат
среднюю арифметическую![]() ;
;
3) возводят в квадрат
каждую варианту ряда
![]() ;
;
4) находим сумму
квадратов вариант
![]() ;
;
5) делят сумму
квадратов вариант на их число, т.е.
определяют средний квадрат
![]() ;
;
6) определяют
разность между средним квадратом
признака и квадратом средней
![]() .
.
Пример 5.
Имеются следующие
данные о производительности труда
рабочих:
Таблица
6.4
|
Табельный |
Произведено |
|
|
1 |
8 |
64 |
|
2 |
9 |
81 |
|
3 |
10 |
100 |
|
4 |
11 |
121 |
|
5 |
12 |
144 |
|
ИТОГО |
50 |
510 |
Произведем следующие
расчеты:
![]() шт.
шт.
![]()
Пример 6.
Определить дисперсию
в дискретном ряду распределения,
используя табл. 6.5.
Таблица 6.5.
|
Произведено |
Число |
|
|
|
|
8 |
7 |
56 |
64 |
448 |
|
9 |
10 |
90 |
81 |
810 |
|
10 |
15 |
150 |
100 |
1500 |
|
11 |
12 |
132 |
121 |
1452 |
|
12 |
6 |
72 |
144 |
864 |
|
ИТОГО |
50 |
500 |
510 |
5074 |
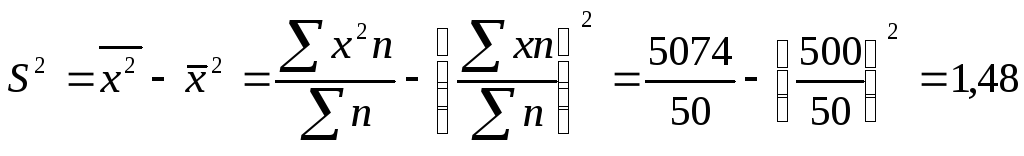
Получим тот же
результат, что в табл. 6.3.
Рассмотрим расчет
дисперсии в интервальном ряду
распределения.
Порядок расчета
дисперсии взвешенной (по формуле
![]() ):
):
-
определяют среднюю
арифметическую
 ;
; -
возводят в квадрат
полученную среднюю
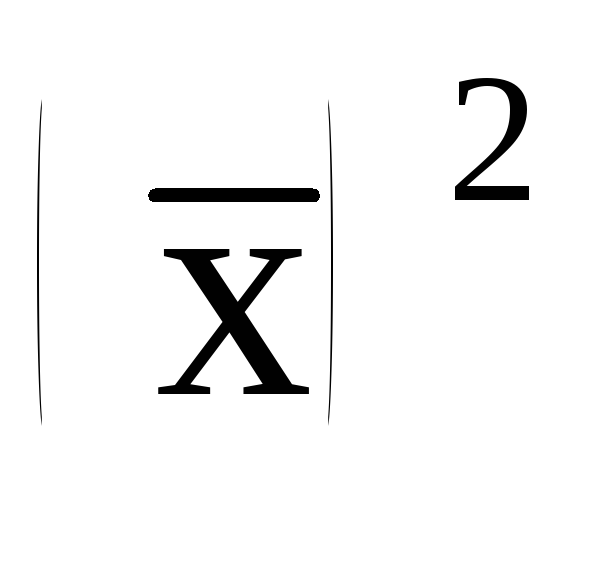 ;
; -
возводят в квадрат
каждую варианту ряда
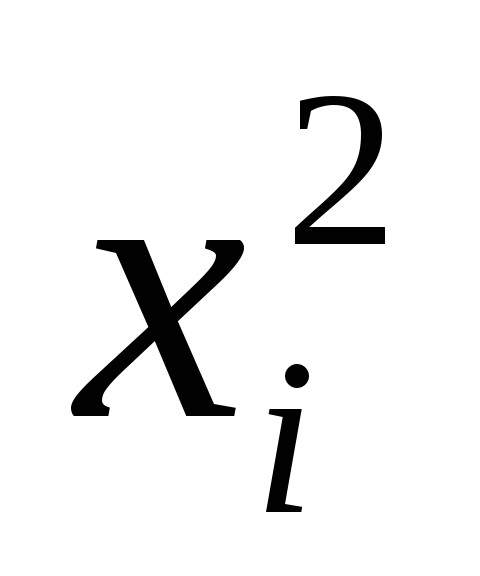 ;
; -
умножают квадраты
вариант на частоты
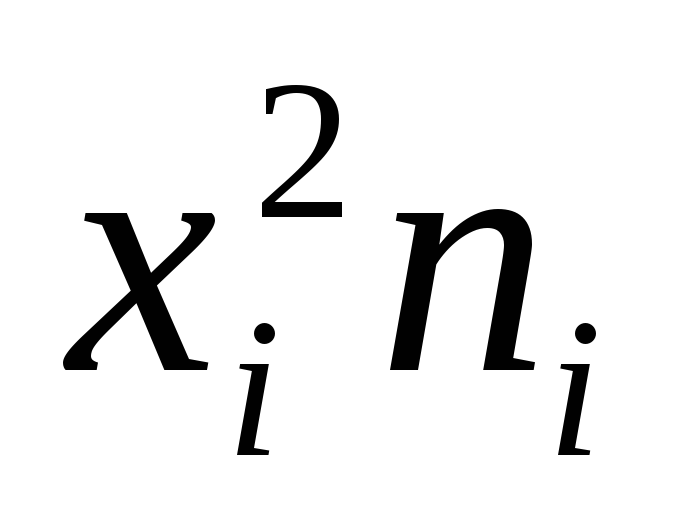 ;
; -
суммируют полученные
произведения
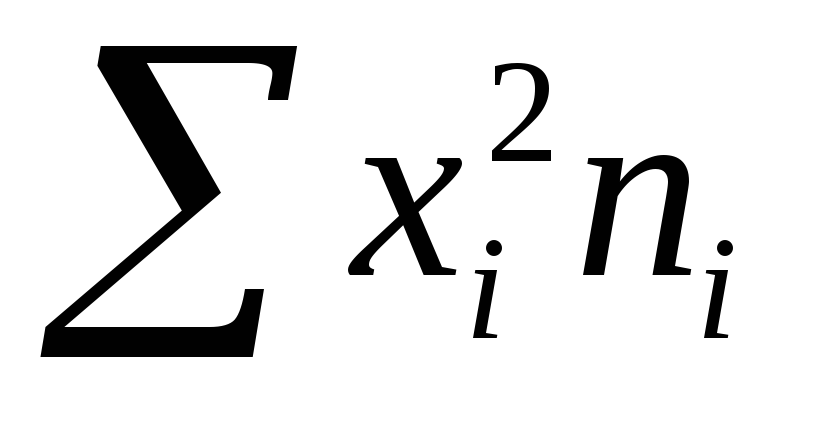 ;
; -
делят полученную
сумму на сумму весов и получают средний
квадрат признака
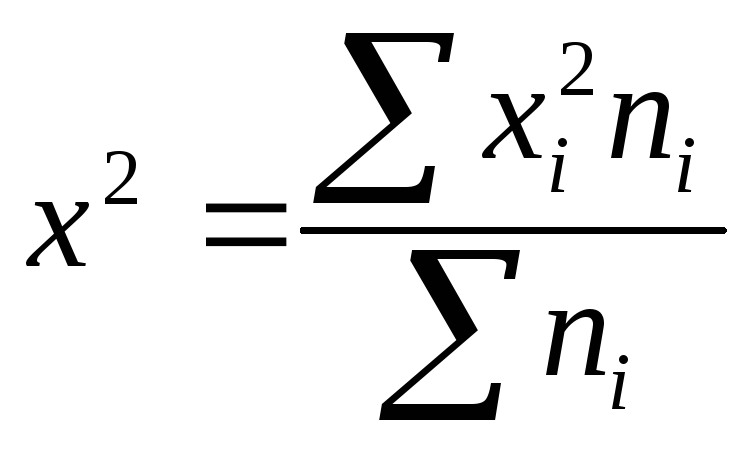 ;
; -
определяют разность
между средним значением квадратов и
квадратом средней арифметической, т.е.
дисперсию
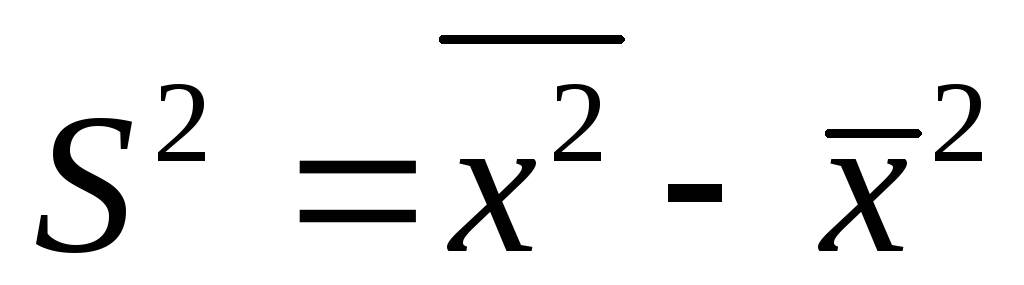 .
.
Пример 7.
Имеются следующие
данные о распределении посевной площади
колхоза по урожайности пшеницы:
Таблица 6.6
|
Урожайность |
Посевная |
|
|
|
|
|
14 |
100 |
15 |
1500 |
225 |
22500 |
|
16 |
300 |
17 |
5100 |
289 |
36700 |
|
18 |
400 |
19 |
7600 |
361 |
144400 |
|
20 |
200 |
21 |
4200 |
441 |
88200 |
|
ИТОГО |
1000 |
18400 |
341200 |
В подобных примерах
прежде всего определяется дискретное
значение признака в каждом интервале,
а затем применяется метод расчета,
указанный выше:

Средняя величина
отражает тенденцию развития, т.е.
действие главных причин. Среднее
квадратическое отклонение измеряет
силу воздействия прочих факторов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Онлайн-калькулятор дисперсии поможет вам определить дисперсию, сумму квадратов и коэффициент дисперсии для определенного набора данных. Кроме того, этот калькулятор также отображает среднее значение и стандартное отклонение путем пошагового расчет дисперсии онлайн. Прочтите, чтобы узнать, как найти дисперсию онлайн и стандартное отклонение, используя формулу выборочной дисперсии.
Что такое дисперсия?
Дисперсия группы или набора чисел – это число, которое представляет «разброс» набора. Формально это квадрат отклонения набора от среднего и квадрат стандартного отклонения.
Другими словами, небольшая дисперсия означает, что точки данных имеют тенденцию быть близкими к среднему и очень близко друг к другу. Высокая дисперсия указывает на то, что точки данных далеки от среднего значения и друг от друга. Дисперсия – это среднее значение квадрата расстояния от каждой точки до среднего.
Типы дисперсии:
Вариация выборки: дисперсия выборки не охватывает всю возможную выборку (случайная выборка людей).
Дисперсия населения: дисперсия, которая измеряется для всего населения (например, всех людей).
Однако онлайн-калькулятор стандартного отклонения позволяет определить стандартное отклонение (σ) и другие статистические измерения данного набора данных.
Формулы отклонения:
Формула дисперсии совокупности
дисперсия формула (совокупности):
Дисперсия (обозначается как σ2) выражается как среднеквадратическое отклонение от среднего для всех точек данных. Мы пишем:
$$ σ2 = ∑ (xi – μ) ^ 2 / N $$
где,
- σ2 – дисперсия;
- μ – среднеквадратическое значение; а также
- xᵢ представляет i-ю точку данных среди N общих точек данных.
Вы можете рассчитать его с помощью калькулятора дисперсии генеральной совокупности, в противном случае есть три шага для оценки дисперсии:
- Чтобы найти разницу между средним значением точки, используйте формулу: xi – μ
- Теперь возьмите в квадрат разницу между средним значением каждой точки: (xi – μ) ^ 2
- Затем найдите среднее квадратическое отклонение от среднего: ∑ (xi – μ) ^ 2 / N.
Это дисперсия формула совокупности.
Пример формулы отклонения
Уравнение выборки дисперсии имеет следующий вид:
s2 = ∑ (xi – x̄) 2 / (N – 1)
где,
s2 – оценка дисперсии;
x – выборочное среднее; а также
xi – i-я точка данных среди N общих точек данных.
Как рассчитать дисперсию?
Чтобы найти среднее значение данного набора данных. Подставьте все значения и разделите на размер выборки n.
ni = 1x дюйм x = ∑ i = 1 nx дюйм
Теперь найдите среднюю разницу значений данных, вам нужно вычесть среднее значение данных и возвести результат в квадрат.
(хи – х) ^ 2 (хи – х) ^ 2
Затем вычислите квадратичные разности и сумму квадратов всех квадратичных разностей.
S = ∑ I = 1n (xi – x) ^ 2
Итак, найдите дисперсию, дисперсия формула генеральной совокупности:
Дисперсия = σ ^ 2 = Σ (xi – μ) ^ 2
Уравнение дисперсии набора данных выборки:
Дисперсия = s ^ 2 = Σ (xi – x) ^ {2n − 1}
Эти формулы запоминать не нужно. Чтобы вам было удобно, наш примерный калькулятор дисперсии выполняет все расчет дисперсии онлайн, связанные с дисперсией, автоматически, используя их.
Тем не менее, Калькулятор диапазона среднего среднего значения режима поможет вам рассчитать средний средний режим и диапазон для введенного набора данных.
Пример расчета
Давайте посчитаем дисперсию оценок пяти студентов на экзамене: 50, 75, 89, 93, 93. Выполните следующие действия:
- Найдите среднее
Чтобы найти среднее значение (x), разделите сумму всех этих значений на количество точек данных:
х = (50 + 75 + 89 + 93 + 93) / 5
х̄ = 80
- Вычислите разницу между средним значением и квадратом отличий от среднего. Следовательно, среднее значение равно 80, мы используем формулу для вычисления разницы от среднего:
xi – x̄
Первая точка – 50, поэтому разница от среднего составляет 50 – 80 = -30.
Квадрат отклонения от среднего – это квадрат предыдущего шага:
(xi – x̄) 2
Итак, квадрат отклонения равен:
(50 – 80) 2 = (-30) 2 = 900
В приведенной ниже таблице квадрат отклонения рассчитан на основе среднего значения всех результатов испытаний. Столбец «Среднее отклонение» – это результат минус 30, а столбец «Стандартное отклонение» – это столбец перед квадратом.
| Счет | Отклонение от среднего | Квадратное отклонение |
| 50 | -30 | 900 |
| 75 | -5 | 25 |
| 89 | 9 | 81 |
| 93 | 13 | 169 |
| 93 | 13 | 169 |
- Рассчитайте стандартное отклонение и дисперсию
Затем используйте квадраты отклонений от среднего:
σ2 = ∑ (xi – x̄) 2 / N
σ2 = (900 + 25 + 81 + 169 + 169) / 5
σ2 = 268,5
дисперсия случайной величины онлайн результатов экзамена составила 268,8.
Как работает калькулятор дисперсии?
Онлайн-калькулятор дисперсии совокупности вычисляет дисперсию для заданных наборов данных. Вы можете просмотреть работу, проделанную для расчет дисперсии онлайн из набора данных, следуя этим инструкциям:
Вход:
- Сначала введите значения набора данных через запятую.
- Затем выберите дисперсию для выборки или совокупности.
- Нажмите кнопку «Рассчитать», чтобы получить результаты.
Выход:
- Калькулятор дисперсии выборки отображает дисперсию, стандартное отклонение, количество, сумму, среднее значение, коэффициент дисперсии и сумму квадратов.
- Этот калькулятор также обеспечивает пошаговые вычисления дисперсии, коэффициента дисперсии и стандартного отклонения.
ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ:
В чем разница между стандартным отклонением и дисперсией?
Дисперсия – это квадрат отклонения от среднего, а стандартное отклонение – это квадратный корень из числа. Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры).
Значение высокой дисперсии – это плохо или хорошо?
Низкая дисперсия связана с меньшим риском и более низкой доходностью. Акции с высокой дисперсией обычно выгодны для агрессивных инвесторов с меньшим неприятием риска, в то время как акции с низкой дисперсией обычно выгодны для консервативных инвесторов с более низкой толерантностью к риску.
Каков диапазон отклонений?
Диапазон – это разница между высоким и низким значением. Поскольку используются только крайние значения, потому что эти значения будут сильно на него влиять. Чтобы найти диапазон отклонения, возьмите максимальное значение и вычтите минимальное значение.
Заключение:
Воспользуйтесь этим онлайн-калькулятором дисперсии, который работает как с выборкой, так и с наборами данных о генеральной совокупности, используя формулу генеральной и выборочной дисперсии. Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.
Other Languages: Variance Calculator, Varyans Hesaplama, Calculadora De Variancia, Kalkulator Varians, Kalkulator Wariancji, Výpočet Rozptylu, 分散 計算.
