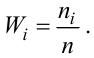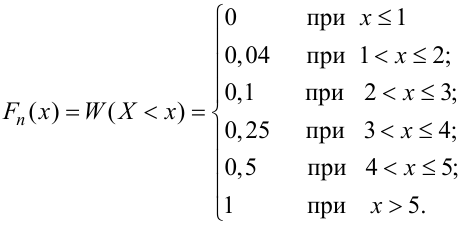Равномерное случайное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Равномерным называют распределение вероятностей непрерывной случайной величины
, если на интервале
, которому принадлежат все возможные
значения
, плотность сохраняет постоянное значение.
Функция распределения
равномерного закона:
Числовые характеристики равномерного распределения
Математическое ожидание равномерно распределенной случайной величины:
Дисперсия
равномерного случайного
распределения:
Среднее квадратическое отклонение случайной величины, распределенной равномерно:
Для равномерного распределения коэффициент асимметрии:
Коэффициент эксцесса
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Кроме равномерного, основные законы распределения непрерывных случайных величин:
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Экспоненциальный (показательный) закон распределения случайной величины
Примеры решения задач
Пример 1
Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность вероятности
равномерного распределения на интервале
:
Искомая вероятность:
Ответ:
.
Пример 2
Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).
Решение
Плотность
вероятности случайной величины, распределенной равномерно на интервале
В нашем
случае
Получаем:
Функцию
распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
Построим
графики:
График плотности распределения
График функции распределения
Математическое
ожидание величины, распределенной равномерно:
Дисперсия:
Среднее
квадратическое отклонение:
Пример 3
Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
равномерного распределения:
Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:
Ответ:
Пример 4
Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.
Решение
Дисперсия
равномерного распределения:
при
начале интервала
:
Искомый
интервал времени:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Случайные
величины X2, X3, X4 имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<Xi<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.
Задача 2
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, xmod, xmed, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.
Задача 3
Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].
Найти:
1) дифференциальную и интегральную
функцию распределения, а также построить их графики.
2) математическое ожидание и
дисперсию;
2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).
Задача 5
Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.
Задача 6
Равномерно распределенная случайная
величина
задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).
Задача 7
Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x0.2.
Задача 8
Случайная
величина
равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).
Задача 9
Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].
Задача 10
Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?
Задача 11
Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].
Задача 12
Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.
Задача 13
СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.
Задача 15
Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.
Задача 16
Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].
Задача 17
Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).
Задача 18
По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.
Задача 19
Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.
Задача 20
Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Как найти дисперсию?
Спасибо за ваши закладки и рекомендации
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 января 2023 года; проверки требуют 2 правки.
У этого термина существуют и другие значения, см. Дисперсия.
Диспе́рсия случа́йной величины́ — мера разброса значений случайной величины относительно её математического ожидания. Обозначается ![D[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa482bb7dcd759ae8e7e38fa47bea024feb50892)



Квадратный корень из дисперсии, равный 
Из неравенства Чебышёва следует, что вероятность того, что значения случайной величины отстоят от математического ожидания этой случайной величины более чем на 

Определение[править | править код]
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Пусть 
где символ 
Замечания[править | править код]
где 




Доказательство 2-й формулы
где 
- Для получения несмещённой оценки дисперсии случайной величины значение
необходимо умножить на
. Несмещённая оценка имеет вид:
Свойства[править | править код]
Условная дисперсия[править | править код]
Наряду с условным математическим ожиданием ![{displaystyle mathbb {E} [X|Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a84d6dab33ae8233f10a39a5b8d346c223b5298)
![{displaystyle D[X|Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fd009ffa0ed890e534a5870b243ff4c8f901a75)
Условной дисперсией случайной величины 

.
Её свойства:
- откуда, в частности, следует, что дисперсия условного математического ожидания
всегда меньше или равна дисперсии исходной случайной величины
.
Пример[править | править код]
Пусть случайная величина 
![{displaystyle displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3c46b95603c311eaa541789bf49b6666d7f48f)
Тогда математическое ожидание квадрата случайной величины равно
,
и математическое ожидание случайной величины равно
Дисперсия случайной величины равна
См. также[править | править код]
- Среднеквадратическое отклонение
- Моменты случайной величины
- Ковариация
- Выборочная дисперсия
- Независимость (теория вероятностей)
- Скедастичность
- Абсолютное отклонение
- Дельта-метод
Примечания[править | править код]
- ↑ Колмогоров А. Н. Глава IV. Математические ожидания; §3. Неравенство Чебышева // Основные понятия теории вероятностей. — 2-е изд. — М.: Наука, 1974. — С. 63—65. — 120 с.
- ↑ Боровков А. А. Глава 4. Числовые характеристики случайных величин; §5. Дисперсия // Теория вероятностей. — 5-е изд. — М.: Либроком, 2009. — С. 93—94. — 656 с.
Литература[править | править код]
- Гурский Д., Турбина Е. Mathcad для студентов и школьников. Популярный самоучитель. — СПб.: Питер, 2005. — С. 340. — ISBN 5469005259.
- Орлов А. И. Дисперсия случайной величины // Математика случая: Вероятность и статистика — основные факты. — М.: МЗ-Пресс, 2004.
Содержание:
- Примеры с решением
Разность 
Дисперсией, или рассеянием, случайной величины X называется математическое ожидание квадрата ее отклонения:
Из определения и свойств математического ожидания следует, чтс дисперсия любой случайной величины неотрицательна, т.е.
Для вычисления дисперсии применяется формула
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Дисперсия случайной величины обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
Возможно вам будут полезны данные страницы:
Замечание.
Свойство 3 распространяется на п независимых случайных величин:
Дисперсия дискретной случайной величины с законом распределения
определяется формулой
или формулой
где
– другое обозначение для математического ожидания. Этим обозначением будем пользоваться и в дальнейшем, в зависимости от обстоятельств.
Если дискретная случайная величина принимает бесконечную по-следовательность-значений с законом распределения
то ее дисперсия определяется формулой
при условии, что этот ряд сходится.
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку 

где р(х) – плотность распределения вероятностей этой величины, 
Дисперсию можно вычислять по формуле

Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку 

если этот несобственный интеграл сходится.абсолютно.
Средним квадратическим отклонением, или стандартным отклонением, случайной величины X называется корень квадратный из ее дисперсии:
Это определение имеет смысл, поскольку выполнено условие (2.5.3).
Пример с решением
Пример 1.
Доказать формулы (2.5.1) и (2.5.4).
Решение:
Так как математическое ожидание М(Х) – постоянная величина, математическое ожидание постоянной равно этой постоянной, математическое ожидание разности случайных величин равно разности их математических ожиданий, то
равенство (2.5.1) доказано.
Учитывая свойства математического ожидания, получаем

равенство (2.5.4) доказано.
Пример 2.
Доказать равенства (2.5.5) – (2.5.8).
Решение:
Принимая во внимание определение дисперсии и тот факт, что математическое ожидание постоянной равно этой постоянной, получаем
Из определения дисперсии и свойств математического ожидания следует, что
Для доказательства формулы (2.5.8) воспользуемся формулой (2.5.4):
Равенство (2.5.8) следует из формул (2.5.6) и (2.5.7):
Пример 3.
Дискретная случайная величина X имеет закон распределения

Решение:
По формуле (2.4.3) находим
Запишем закон распределения квадрата отклонения этой величины, т.е. величины

В соответствии с формулой (2.5.16) находим среднее квадратическое отклонение
Замечание. Дисперсию можно вычислить и по формуле (2.5.4). Найдем для этого математическое ожидание квадрата случайной величины X, предварительно записав закон распределения случайной величины X2;

В соответствии с формулой (2.5.4) находим
Пример 4.
Закон распределения дискретной случайной величины X задан таблицей

Решение:
Сначала найдем математическое ожидание случайной величины^:
Запишем закон распределения случайной величины

Квадрат случайной величины X, т.е. X2 – это новая случайная величина, которая с теми же вероятностями, что и случайная величина X, принимает значения, равные квадратам ее значений.
Квадраты значений случайной величины X равны: 





По формуле (2.4.3) находим
Следовательно, по формуле (2.5.4) имеем
Пример 5.
Симметричная монета подбрасывается 4 раза. Случайная величина X- “число выпадений герба при этих подбрасываниях”. Найти числовые характеристики случайной величины
Решение:
Данная дискретная случайная величина X может принимать пять значений: 
Закон распределения случайной величины X можно задать таблицей Находим математическое ожидание
Закон распределения случайной величины 



Пример 6.
Найти дисперсию дискретной случайной величины X -числа очков, выпадающих при подбрасывании игрального кубика.
Решение:
Запишем сначала закон распределения этой случайной величины в виде таблицы


Дисперсию вычислим по формуле (2.5.4):
Пример 7.
Даны все возможные значения дискретной случайной величины


Решение:
Запишем законы распределения дискретных случайных величин X и X2.



Поскольку 
откуда 
Итак, закон распределения случайной величины X определяется таблицей
Пример 8.
Дискретная случайная величина X может принимать только два значения 




Решение:
Поскольку 



Решая систему уравнений
и учитывая условие 

Пример 9.
Найти числовые характеристики 
Решение:
Сначала находим М(Х) по формуле (2.4.7):

В соответствии с формулой (2.5.13) найдем D(X) :
По формуле (2.5.16) находим
Пример 10.
Найти числовые характеристики 
Решение:
С помощью формулы (2.4.7) находим математическое ожидание:
По формулам (2.5.13) и (2.5.16) соответственно получаем

Пример 11.
Случайная величина X задана функцией распределения
Найти числовые характеристики случайной величины
Решение:
Сначала найдем плотность распределения р(х) с помощью формулы (2.3.5). Так как 

По формуле (2.4.7) вычисляем математическое ожидание:
В соответствии с формулами (2.5.13) и (2.5.16) находим дисперсию и среднее квадратическое отклонение:

Пример 12.
Независимые случайные величины 
при 
Решение:
С учетом формулы (2.4.13) и условия (I) находим

т.е. математическое ожидание среднего арифметического п независимых одинаково распределенных случайных величин равно математическому ожиданию каждой из этих величин.
Учитывая формулы (2.5.6), (2.5.9) и условие (I), получаем
т.е. дисперсия среднего арифметического п независимых одинаково распределенных случайных величин в л раз меньше дисперсии каждой из этих величин.
Учитывая определение и условие (I), находим
Таким образом, среднее квадратическое отклонение среднего арифметического n независимых одинаково распределенных случайных величин в 
Лекции:
- Математическое ожидание: пример решения
- Законы распределения случайных величин
- Моменты случайной величины
- Моменты высших порядков
- Метод моментов
- Непрерывные случайные величины примеры с решением
- Числовые характеристики непрерывной случайной величины
- Функция случайной величины
- Математическая дисперсия случайной величины
- Дисперсия суммы случайных величин
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 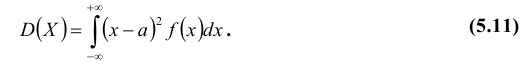
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 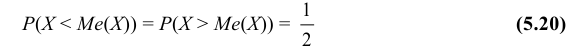
Пример №2
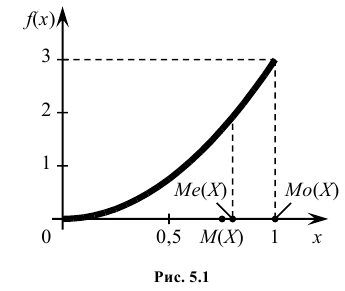
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 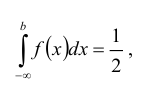
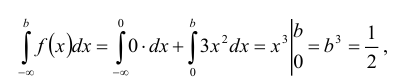
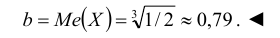
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 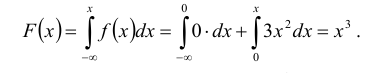
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
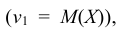
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
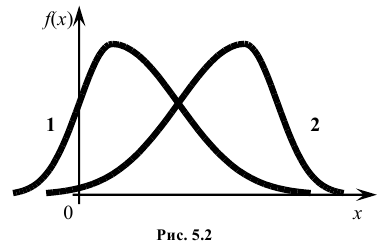
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 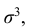
Полученная величина А называется коэффициентом асимметрии случайной величины: 
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
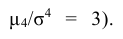
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 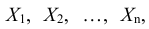
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 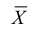
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
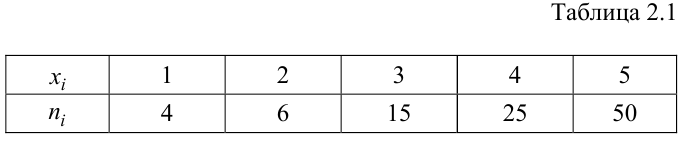
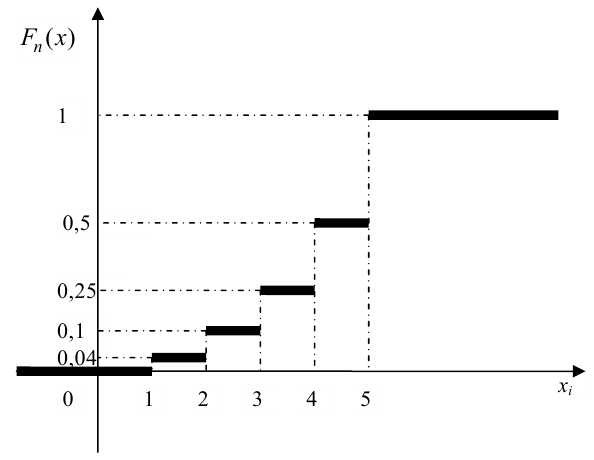
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 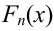
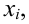
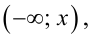
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
![{displaystyle D[X]=mathbb {E} left[{big (}X-mathbb {E} [X]{big )}^{2}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af0036187b87a8c738238bce5853e1d4b0df5d4b)



![{displaystyle D[X|Y]=mathbb {E} [(X-mathbb {E} [X|Y])^{2}|Y]=mathbb {E} [X^{2}|Y]-mathbb {E} [X|Y]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d07e6493949314f0a9dfb7f20d8c774ead57a94b)
![f_{X}(x)=left{{begin{matrix}1,&xin [0,1]\0,&xnot in [0,1].end{matrix}}right.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe7c0979d6e6a936e73de86914b564f78c5db16)
![{displaystyle mathbb {E} left[X^{2}right]=int limits _{0}^{1}!x^{2},dx=left.{frac {x^{3}}{3}}rightvert _{0}^{1}={frac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea35960967b1f07bcc96c2bfd553485ac7704cfd)
![{displaystyle mathbb {E} left[Xright]=int limits _{0}^{1}!x,dx=left.{frac {x^{2}}{2}}rightvert _{0}^{1}={frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cce35565ca3d3e3abeb7d343a40f75e5eb63bda)
![{displaystyle D[X]=mathbb {E} left[X^{2}right]-(mathbb {E} [X])^{2}={frac {1}{3}}-left({frac {1}{2}}right)^{2}={frac {1}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcb8ee8e63837c48b7072b105e89af17b343d862)




























































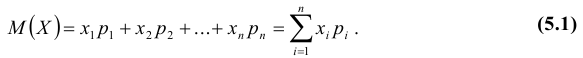
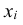
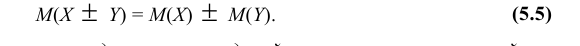


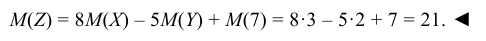







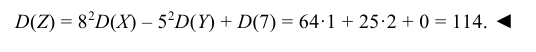
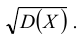

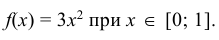

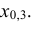
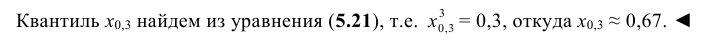



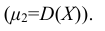
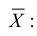
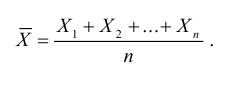

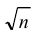 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: